当前位置：文档之家 › 三重积分 柱坐标与极坐标PPT

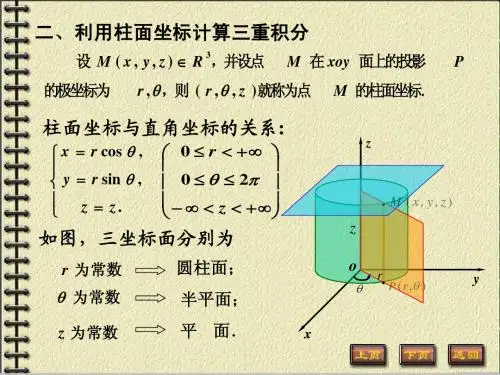
三重积分 柱坐标与极坐标PPT

  • 格式：ppt
  • 大小：4.30 MB
  • 文档页数：50

下载文档原格式

  / 50

合集下载

微积分：利用柱坐标计算三重积分

微积分：利用柱坐标计算三重积分

a Dxy
r
,
cos
x
o
y
z x2 y2
I
4
a
2 4 cos
d d r 2 sin2 r 2 sin dr
x r sin cos
y
r
sin
sin
z r cos
00 0
dv r2 sin drdd
I ( x2 y2 )dxdydz
2
a
d 4 d cos r 2 sin2 r 2 sin dr
2
2
dz d
ze z2 rdr
1
0 0r
2 2 ez2 zdz (e4 e). 1
z
z2
z x2 y2
z1
O
y
x
y Dz
x
x2 y2 z2
计算(x y z)2dv,
其中是抛物面 z
x2
y2和 球 面x2
y2
z
z2
2
所围成的空间闭区域.
解 ( x y z)2 x2 y2 z2 2( xy yz zx)
且 当( x, y) Dxy时, x2 y2 z 2 x2 y2 ,
Dxy : x2 y2 1,
y Dxy
x
x2 y2 z 2 x2 y2,
x2 y2 1
2 x2 y2
V 1 dv dxdy
1 dz
x2 y2
Dxy
(2 2 x 2 2 y 2 )dxdy
Dxy
2
2
d
1 (1 r 2 )rdr
0
0
0
0
t (0, )
0 r t
所以,F (t)在(0, )内 单调增加.

计算三重积分详细方法

计算三重积分详细方法

一般，先对 z 积分，再对 r ，最后对 积分。 6
例1 利用柱面坐标计算三重积分 zdxdyd, z 其中
是由z曲 x2面 y2与平 z面 4所围成的闭
解 (1) 画 图
z
(2) 确定 z，r， 的上下限
44
将 向 xoy 面投影，得
D :x2y24
或
02,
D:
0r2.
o•(r,)
yy
xx
就叫M 点 的柱面坐标． z
规定： 0r,
02 ,
•M (x,y,z)
z . 简单地说，柱面坐标就是
or
y
•
P(r,)
x
xoy 面上的极坐标 + z 坐标
4
如图，三坐标面分别为
r 为常数
为常数
z 为常数
圆柱面； 半平面； 平 面．
柱面坐标与直角坐标的 关系为
x r cos ,
y
r
sin
,
z
z.
z
z
or
y
x
z
M (x ,y,z)
•
o
x
r
y
• P(r,) 5
如图，柱面坐标系中的 体积元素为
d v rdd rd, z
z
rd
dr r dz
于是，
o
y
f(x,y,z)dxdydz
x d
f (r c o ,r ssi,z n )r d dr d . z
再根据 中 z，r， 的关系，化为三次积分。
z
R
任取一 [0,2],过 z
轴作半平面，得
04.
在半平面上，任取一
[0, 4],
x

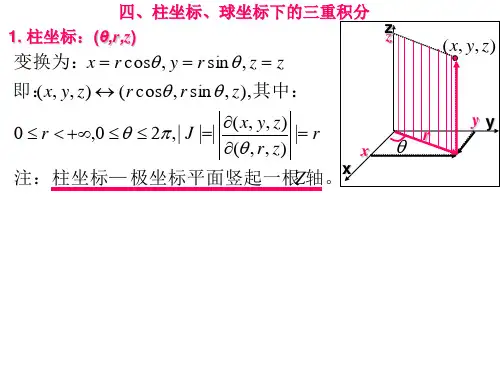
柱坐标、球坐标下的三重积分

柱坐标、球坐标下的三重积分

解：由图知：直角系：
D
y
x
2
4 x2
6x2 y2
I dx
dy
f (x, y, z)dz
2
4x2
x2 y2
柱标系： I
2
d
2
rdr
6r 2
f (r cos , r sin , z)dz
0
0
r
杂例
在三种坐标系下化三重积分 f (x, y, z)dv为三次积分，
z
其中：z 6 x2 y2, z x2 y2 z 6 x2 y2 6
四、柱坐标、球坐标下的三重积分
1. 柱坐标：(θ,r,z)
zz
变换为：x r cos , y r sin , z z
即：(x, y, z) (r cos , r sin , z),其中：
0 r ,0 2 ,| J || (x, y, z) | r ( , r, z)
x
注：柱坐标— 极坐标平面竖起一根Z轴。x
上顶： z 1 x2 y2
下底： z = 0
z
Dxy: x 2 y 2 1
x y
I dxdy
zdz
Dxy
用哪种坐标？ 柱面坐标 .
.
2π
1
1r 2
I = 0 dθ 0 rdr0 zdz
Dxy 0
1
4
x
z0
1y
注：用柱坐标求 fdv分成两个步骤：
第一步：先一后二，对z积分后将二重积分化为极坐 标下的二重积分；
元素区域由六个坐标面围成：
半平面及+d ;
半径为r及 r+dr的园柱面；
平面 z及 z+dz；
dz

极坐标与球面坐标计算三重积分

极坐标与球面坐标计算三重积分

方向转到有向线段
的角．
OP
这样的三个数r、围为
x
0 r<，0 j <，0q 2．
r j
O
q x
M(x, y, z)
y
y
P
坐标面rr0，jj 0，q q 0的意义： z
j O
q
x
ry
点的直角坐标与球面坐标的关系：
x r sin j cosq ,
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标．
三个数 r、q 、z 叫做点M 的柱面坐标．
这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<．
z z
M(x, y, z)
O
2
dq
a
dj
2a cosj r 2 sin jdr
0
0
0
jr
2
a
s in jdj
2a cosj r 2 dr
0
0
a
16a3 a cos3 j sinjdj 30
O
y
4a3 (1 cos4 a) ．
x
3
例3 求均匀半球体的重心．
z
解 取半球体的对称轴为 z 轴， 原点取在球心上，又设球半径为a．
坐标面rr0，q q 0，zz0的意义：
x
z
z0
rr0 O
r0 q0
zz0
q q 0 y
直角坐标与柱面坐标的关系：
z
x r cosq ,
y
r
sin
q
,
z z.

利用柱面坐标计算三重积分

利用柱面坐标计算三重积分
`z
z
j r
zdv

dvΒιβλιοθήκη zdvO
dv

a 2 0 2
．
q
x
a y
dv 2 dj dq


2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分

，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲

面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz

2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2

3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z

§9.5[1]利用柱面坐标和极坐标计算三重积分

§9.5[1]利用柱面坐标和极坐标计算三重积分

再根据 中 z,r,θ 的关系,化为三次积分. , , 的关系,化为三次积分. 积分. 一般, 积分, 一般,先对 z 积分,再对 r ,最后对 θ 积分.
例1 利用柱面坐标计算三重积分
∫∫∫ z dxdydz ,
其中 其中
所围成的闭区域. 是由曲面 z = x2 + y2 与平面 z = 4 所围成的闭区域.
2
A
过 (r, θ )∈D 做平行于 z 轴 ∈ 的直线, 的直线,得
4
z
r2 ≤ z ≤ 4
0 ≤ θ ≤ 2π , : 0 ≤ r ≤ 2, 2 r ≤ z ≤ 4
o (r,θ )
x
y
即
r =2
o
2
于是, 于是,
A
∫∫∫ z dxdydz = ∫∫∫ z r drdθ dz.
= ∫0 dθ ∫0 dr∫r2 r z dz
规定: 规定:
z
0 ≤ r < +∞,
0 ≤ ≤π,
o θ
x
r
M( x, y, z)
y
0 ≤ θ ≤ 2π .
P
z
如图, 如图,三坐标面分别为
r 为常数
球
面;
r
为常数
θ 为常数
圆锥面; 圆锥面; 半平 面.x来自zoθ
y
球面坐标与直角坐标的关系为
x = r sin cosθ , y = r sin sinθ , z = r cos.
= 2π ∫0 (Hr 3 r4 )dr
π H5 . =
10
二,利用球面坐标计算三重积分
设 M( x, y, z) 为空间内一点,则点M 可用三个有次 为空间内一点, 来确定, 序的数r,,θ 来确定,其中r 为原点O 与点 M 间 的距离, θ 轴正向所夹的角, 的距离, 为有向线段OM与z 轴正向所夹的角, 为从正z 轴来看自x 轴按逆时针方向转到有 向线段 OP 的角,这里P 为点 M 在 xoy 面上的投影,这 的角, 面上的投影, 的球面坐标. 样的三个数r,,θ 就叫做点M 的球面坐标.

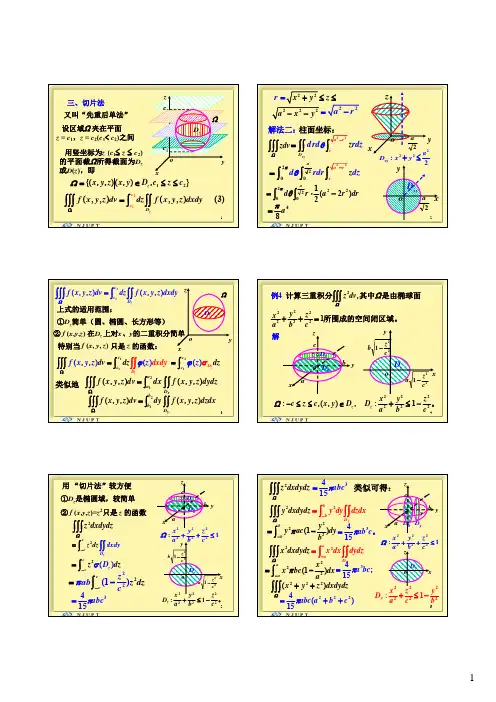
8.3.1 三重积分-直角坐标系切片法,柱面坐标系

8.3.1 三重积分-直角坐标系切片法,柱面坐标系

三、切片法又叫“先重后单法”设区域Ω夹在平面z =c 1，z =c 2(c 1<c 2)之间Ω1c 2c z用竖坐标为z c ≤z ≤c zD 1},),(),,{(21c z c D y x z y x z ≤≤∈=Ωyxo (12)的平面截Ω所得截面为D z 或D (z )，即21(,,)(,,) (3)zc c D f x y z dv dz f x y z dxdy Ω=⎰⎰⎰⎰⎰⎰柱解法二：面坐标：⎰⎰⎰zdv ∙yzxo2a 2a 22222x y z a x y +≤≤--22a r=-r =22r ra z d rd rdz θ-=⎰⎰⎰22a yxo⎰⎰-⋅=202220)2(21a dr r a r d πθΩ48a π=xyD 22:2xy D x y +≤xyD 22220a r ra z d rdr dzπθ-=⎰⎰⎰ΩzyozD ⎰⎰⎰⎰⎰⎰=zD c c dxdy z y x f dz dv z y x f ),,(),,(21Ω特别当f (x , y , z ) 只是z 的函数：②f (x ,y ,z ) 在D z 上对x 、y 的二重积分简单①D z 简单（圆、椭圆、长方形等）上式的适用范围：3x类似地⎰⎰⎰⎰⎰⎰=ΩxD a adydzz y x f dx dv z y x f ),,(),,(21⎰⎰⎰⎰⎰⎰=ΩyD b bdzdxz y x f dy dv z y x f ),,(),,(2121(,,)()zc c D dxd dv d f y z y x z z ϕΩ=⎰⎰⎰⎰⎰⎰21()z c c D z dzϕσ=⎰解2222222,14z dv y z x a b c ΩΩ++=⎰⎰⎰计算三重积分其中是由椭球面所围成的空间例闭区域。

zc y 21z b -4,),(,:z D y x c z c ∈≤≤-Ω。

2222221:c z b y a x D z -≤+D 0D z xyz ab o zD 221cz a -x o2c ⎰⎰⎰Ωdxdydzz 2D 0D z z x yz ab oc ①D z 是椭圆域，较简单②f (x ,y ,z )=z 2只是z 的函数用“切片法”较方便1:222222≤++cz b y a x Ω2cz 53154abcπ=zD 221c z a -yx o221c zb -。

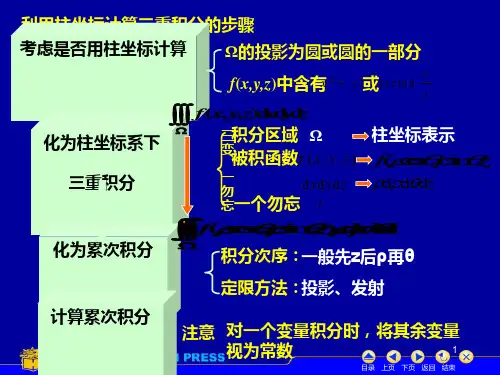
D10_3三重积分 柱坐标与极坐标

D10_3三重积分 柱坐标与极坐标
利用柱坐标计算三重积分的步骤
考虑是否用柱坐标计算
化为柱坐标系下 三重积分
积分次序：
定限方法：
化为累次积分
计算累次积分
注意
对一个变量积分时，将其余变量视为常数
Ω的投影为圆或圆的一部分
f(x,y,z)中含有
或
三变、一勿忘
积分区域
Ω
积分区域
Ω
球坐标表示
被积函数
体积元素
一个勿忘
一般先r后φ再θ．
观察、想象．
三重积分的定义和计算
在直角坐标系下的体积元素
（计算时将三重积分化为三次积分）
小结
方法1. “先一后二”
方法2. “先二后一”
2. 确定上下曲面函数，得 z的积分限;
1. 把Ω往xoy平面上投影,得积分区域D;
4. 最后计算单积分
第三节
一、三重积分的概念
二、三重积分的计算
三重积分
第十章
回忆用投影法（先一后二）计算三重积分
如果积分区域 在坐标面上的投影区域 D 是圆域
则二重积分应当考虑用极坐标计算.
这就等于用柱面坐标计算三重积分.
2. 利用柱坐标计算三重积分
2. 利用柱坐标计算三重积分
于所求立体的体积为
此球面的方程为x2y2(za)2a2 即x2y2z22az
例6.
的立体的体积
由圆锥面和球面围成 ,
解:
采用球面坐标，
锥面方程为
在球面坐标下球面方程为r2acos ,
例7. 计算三重积分
解: 在球面坐标系下
所围立体.
其中
面
是由两个球
解:
例7. 计算三重积分

§135 三重积分及柱坐标计算法与球坐标计算法

§135 三重积分及柱坐标计算法与球坐标计算法

§13-5 三重积分及柱坐标计算法与球坐标计算法§13-5 三重积分的柱坐标计算法与球坐标计算法158 158§13-5 三重积分的柱坐标计算法与球坐标计算法1.柱坐标计算法 当积分区域Ω在直角坐标系中向某个坐标平面的垂直投影是圆或圆的一部分时，时常采用柱坐标计算三重积分。

读者从图13-26中看出，点(,,)P r z θ的柱坐标实际上是它到Oxy 坐标平面上垂足N 的平面极坐标(,)r θ与点P 的竖坐标z 的组合。

根据定理13-5和二重积分的极坐标计算法，可得下面关于三重积分的柱坐标计算法。

定理13-6 在定理13-5的假设条件下，则有21(cos ,sin )(cos ,sin )(,,)d d d d d (cos ,sin ,)d r z r r D z r r f x y z x y z r r f r r z z θθθΩθθθθθ=⎰⎰⎰⎰⎰⎰(13-28)其中rD θ是Ω在Oxy 坐标平面上的垂直投影（图13-27）。

例17 求三重积分d d d z x y z Ω=⎰⎰⎰I ，其中Ω是由球面2224x y z ++=的上半球面与抛物面223xy z+=围成的区域cos ,sin )r θθ图图cos ,sin )r θθ§13-5 三重积分的柱坐标计算法与球坐标计算法 159159（图13-28⑴）。

解 题中球面与抛物面的柱坐标方程依次为2222r z +=与23r z =。

它们围成的区域Ω在Oxy 坐标平面上的垂直投影为圆(3)rD r θ≤。

根据式（13-28），222422π320031d d d d (4)d 29rz r r D z r r r z z r r θθθ=-=⎡⎤==--⎢⎥⎣⎦⎰⎰⎰⎰⎰I354633209113π4d π2π6π9454424r r r r r r r ⎫⎛⎫⎛⎫=--=--=--=⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰2.球坐标计算法 当积分区域Ω是球体或球体的一部分时，时常采用球坐标计算三重积分。

三重积分(2)

三重积分(2)
y

y
球面坐标与直角坐标的关系: x r sin cos , 0 r y r sin sin , 0 2 z r cos . 0 如图，三坐标面分别为
r 为常数
x
P
球 面； 半平面; 圆锥面.


z ln( x y z 1 )
2 2 2
x y z 1
2 2 2
dxdydz
其中积分区域 {( x , y , z ) | x 2 y 2 z 2 1 } .
解 积分域关于 xoy 坐标面对称，
被积函数是 z 的奇函数,


z ln( x y z 1 )
二、利用柱面坐标计算三重积分
设 M ( x , y , z ) R ，并设点
3
M 在 xoy 面上的投影 M 的柱面坐标．
z
P
的极坐标为
r , ，则 ( r , , z ) 就称为点
柱面坐标与直角坐标的关系:
x r cos , y r sin , z z.
y2 2z 解1 由 x 0
旋转面方程为
2 2
绕
oz
轴旋转得，
x y 2z,
2 2
令 D 1 : x y 16 ,
D2 : x y 4,
2 2
D1
D2
I

D1
dxdy
2

8 x y 2
2 2
( x y )dz
2 2

D2
dxdy

2
2 x y 2

( x z ) dv

课件：三重积分的计算(柱坐标和球面坐标)

课件：三重积分的计算(柱坐标和球面坐标)

9
旋转面方程为 x2 y2 2z,
I 28dz ( x2 y2 )dxdy
Dz
28dz ( x2 y2 )dxdy x2 y22z
28dz 02 d 0 2z r 3dr
282
4z2 dz 4
336。
例 3．一形体 是由平面yz4, z0和圆柱面
x2 y2 16 所围成，已知其上任一点的密度与该
点到 z 轴的距离 成正比，求其质量 m 。
解：密度函数 ( x, y,z)k x2 y2 (k0) ，则 z
m k x2 y2 dxdydz 。
x2 y2 16
yz4
4
在 xoy 平面上的投影区域为 Dxy {( x, y) x2 y2 16} ，
o 4y
x
10
在柱面坐标下
{(,,z) 02, 04, 0 z4sin } ，
x sincos rcoscos rsinsin
∵ J ( x, y,z) sinsin rcossin rsincos r 2sin
( r ,,)
cos rsin
0
∴ f (x, y,z)dxdydz
f (rsincos,rsinsin,rcos)r2 sindrdd
24
sincos rcoscos rsinsin
奇函数， 有 xdv 0.
( x z)dv zdv 利用球面坐标
2
d
4 d
1 r cos r2 sin dr
.
0
0
0
8
例6 计算 e z dv， : x2 y2 z2 1.
解 被积函数仅为 z 的函数，截面 D(z) 为圆域 x2 y2 1 z2，故采用＂先二后一＂法．

柱面坐标系.

柱面坐标系.

I 0 d 0 d 0 r r sin dr
2 2
2


2
2 0 sin d 0 r dr
4

2
16 2 . 5
五、小结
三重积分换元法
柱面坐标 球面坐标
（1） 柱面坐标的体积元素
dxdydz rdrddz
（2） 球面坐标的体积元素
dxdydz r sin drdd
则 OA x , AP y, PM z .
A
r

M ( x, y, z )
z
o

球面坐标与直角坐标的关系为
x
y
P

y
x r sin cos , y r sin sin , z r cos .
四 利用球面坐标计算三重积分
z
球面坐标系中的体积元素为
2


2



4 0
4
1 2a sin cos d |0 4
2
a
由x y z z 例 4 计算 x y z dv , 其中
2 2 2
2 2 2

2 2 2 x y z 2 z 所围空间闭区域． 和 为0 2 ,0 , cos r 2 cos ． 解 2
I ( x y )dxdydz d rdr r 2 dz 0 0 r
2 2
2
a
a
a a 5 2 0 r (a r )dr 2 [a ] a . 4 5 10
a
4 5

3
补充：利用对称性化简三重积分计算

重积分应用PPT课件

重积分应用PPT课件

01
球面坐标系的建立
以原点为球心，以r为半径的球面将空间划分为若干个球面区域。
02
球面坐标系下三重积分的计算
将三重积分转化为球面坐标系下的二重积分，再对r、θ和φ进行积分。
03
典型例题解析
通过具体例题展示球面坐标系下三重积分的计算过程。
典型例题解析
01
02
03
04
例题1
计算球体体积（直角坐标系下 ）。
典型例题解析
例题一
求解二重积分$int_{0}^{1}int_{0}^{1}e^{-(x^2+y^2)}dxdy$， 分别采用矩形法、梯形法和Simpson法进行求解，并比较各方 法的精度和计算量。
例题二
求解二重积分$int_{0}^{pi}int_{0}^{pi}sin(x+y)dxdy$，分别 采用矩形法、梯形法和Simpson法进行求解，并分析各方法的 适用性。
03
三重积分计算方法
直角坐标系下三重积分计算
投影法
将三重积分投影到三个坐标面上， 分别计算每个投影区域上的二重
积分，再相加得到最终结果。
截面法
通过平行于坐标面的平面截取积 分区域，对每个截面上的二重积 分进行计算，再对截面进行积分
得到最终结果。
先一后二法
先对其中一个变量进行积分，将 三重积分转化为二重积分，再对
剩余两个变量进行积分。
柱面坐标系下三重积分计算
1 2
柱面坐标系的建立
以原点为顶点，以z轴为对称轴的圆柱面将空间 划分为若干个柱面区域。
柱面坐标系下三重积分的计算
将三重积分转化为柱面坐标系下的二重积分，再 对r和θ进行积分。
3
典型例题解析

高等数学随堂讲解三重积分在柱坐标与球坐标系下计算

高等数学随堂讲解三重积分在柱坐标与球坐标系下计算

一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
➢柱坐标系 平面极坐标系添加oz轴得到的空间坐标系
➢柱坐标 设 M (x, y, z) R3,
➢直角坐标与柱坐标的关系
x cos
点M的柱坐标
z
y sin
zz
z M (x, y, z)
规定
在柱坐标系下
常数 常数
圆柱面 半平面
o
y
x (x, y,0)
z 常数
平面
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
➢球坐标系下三重积分计算公式
f (x, y, z)dv f (r sin cos , r sin sin , r cos )r 2 sin drdd
二、三重积分在球坐标系下的计算
（一）球坐标系 （二）球坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
二、三重积分在球坐标系下的计算
三重积分在柱坐标和球坐标系下的计算
一、三重积分在柱坐标系下的计算 二、三重积分在球坐标系下的计算
三重积分在柱坐标和球坐标系下的计算
一、三重积分在柱坐标系下的计算 二、三重积分在球坐标系下的计算
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
（一）球坐标系 （二）球坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法

极坐标与球面坐标计算三重积分课件

极坐标与球面坐标计算三重积分课件
三重积分的性质
三重积分的性质包括可加性、可移性、 可换序性等，这些性质在计算三重积 分时有着重要的应用。
三重积分的计算方法概述
1 2 3
直角坐标系下的三重积分计算 在直角坐标系下，三重积分可以通过将积分区域 划分为立方体网格，然后对每个立方体进行积分 计算。
极坐标系下的三重积分计算 极坐标系下，三重积分可以通过将积分区域划分 为球心在原点的球壳，然后对每个球壳进行积分 计算。
球面坐标系下的三重积分计算 球面坐标系下，三重积分可以通过将积分区域划 分为以原点为球心的球体，然后对每个球体进行 积分计算。
三重积分的基本应用
体积计算
三重积分可以用于计算三维空间中物体的体积，例如球体、圆柱 体等。
质量计算
三重积分可以用于计算分布在不同区域的质量，例如分布在平面 或曲面上的质量。
极坐标系与直角坐标系的转换
直角坐标系转换为极坐标系
给定直角坐标系中的一点，可以将其转换为极坐标系中的点。 通过计算点到原点的距离和与极轴之间的角度即可得到该点 的极坐标。
极坐标系转换为直角坐标系
给定极坐标系中的一点，可以将其转换为直角坐标系中的点。 通过计算该点在极轴上的投影和在极平面上的投影即可得到 该点的直角坐标。
03
利用极坐标系下表达形式，将 三维空间的乘积转化为极坐标 系下的乘积。
极坐标系下计算三重积分的常见问题
确定积分区域的形状和范围时，容易出现错误。
01
02
在将三重积分转化为三次积分时，容易出现错误。
在利用极坐标系下表达形式计算三维空间的乘积时，容易出现
03
错误。
PART 05
三重积分在球面坐标系下 的计算
根据被积函数的形状和极坐标系 下表达形式，确定积分区域的形

极坐标与球面坐标计算三重积分

极坐标与球面坐标计算三重积分
4 3
3 a
2π
π
4 其中 M = πa 3 ρ 为球体的质量． 3
0
2πa 3 , r 2 sin ϕdr = 3
a
1 a4 zdv = ∫ 2 dϕ ∫ dθ ∫ r cos ϕ ⋅ r 2 sin ϕdr = ⋅ 2π ⋅ , ∫∫∫ 0 0 0 2 4 Ω 3a 3a 因此z= ．重心为(0，0， )． 8 8
2π
π
例4 求均匀球体对于过球心的一条轴l 的转动惯量． 解 取球心为坐标原点，z轴与轴l重合，又设球的半径为a， z 则球体所占空间闭区域Ω可用不等式 x2+y2+z2≤a 2 来表示． 所求转动惯量为
θ =θ 0
y
θ0
直角坐标与柱面坐标的关系：
z z M(x, y, z)
x = r cos θ , y = r sin θ , z = z.
柱面坐标系中的体积元素： dv =rdrdθdz． 柱面坐标系中的三重积分： x
Ω
O x
θ
r
y P(r, θ )
y
∫∫∫ f (x，y，z)dxdydz = ∫∫∫ f (r cos θ
V= ∫∫∫ dxdydz = ∫∫∫ r2 sinϕ drdϕdθ
Ω Ω
= ∫ dθ ∫ dϕ ∫
0 0
2π
α
2 a cos ϕ
0
r 2 sin ϕdr
= 2π ∫ sin ϕdϕ ∫
0
α
2 a cos ϕ
ϕ r α O x y
0
r 2 dr
16πa 3 α = cos 3 ϕ sin ϕdϕ 3 ∫0 4πa 3 = (1 − cos 4 a) ． 3

9-3(2)三重积分

9-3(2)三重积分

3、在球面坐标系下将三重积分化为三次单积分
主要有两种情况：
1° 的边界曲面是一个包围原点在内的闭曲面。
曲面坐标为r r ( , )
则 I d d
0 0 2

r ( , )
0
F ( r , , )r 2 sindr
其中 : F ( r , , ) f ( r sin cos , r sin sin , r cos )
rsind
半径为r及r+dr的球面；
dV
r

圆锥面及+d
dv r sindrdd ,
2
f ( x, y, z )dxdydz

0

d
y
2 f ( r sin cos , r sin sin , r cos ) r sindrdd .
dz
dV
平面 z及 z+dz；
dV = rdrddz
f ( x , y , z )dxdydz
.
z
0
d
r
y
f ( r cos , r sin , z ) r drddz

x
底面积 ：r drd
3、在柱面坐标系下将三重积分化为三次单积分
次序通常选择为z ，r ，
0
r dr z dz
2 0
a
2 d
0

2 cos
0
2 2 cos z a 2 2 r dr 2 d r dr 0 0 2 2 0
2 8 a 8a 2 3 d cos d 9 6 0
2 a
a 2
2
r 2 0 3 0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4}
上边界曲面为z 4 下边界曲面为z .
(x2 y2)dv
2
d
2
d
2 2 dz
0
0
dv d ddz
2
2 3d
2
dz 2
2 3(2 )d 16
0
0
5
例3. 计算三重积分
其中 由球面
x2 y2 z2 2与抛物面
x2 y2 z 所围成 .
解:
由 2 z2 2 知交线为
0
0
2
2 π 1 2 (16 2 )d 20
xO y dv d ddz
64 .
3
例2. 计算
(x2 y2 )dv, 其中 由圆锥面
与平面 z 2所围成 .
z x2 y2
解：
由z z
2
x2
y2
得交线 上投影区域为
x2
y2 4, 故在xOy平面
Dxy {(x, y) | x2 y2
设 M (x, y, z) R3,将x, y用极坐标, 代替, 则（, , z)
就称为点M 的柱坐标.
直角坐标与柱面坐标的关系:
x cos y sin
zz
坐标面分别为
常数 常数
z 常数
00z2π
圆柱面 半平面 平面
z z
M (x, y, z)
O
y
x
(x,
y,0)
元素区域由六个坐标面围成
常见曲面的柱面坐标方程
用柱面坐标计算三重积分的一般步骤：
次序为：zr
1、将区域往xoy面上投影，确定平面区域D
2、利用公式
x r cos, y r sin, z z.
将的边界曲面、被积函数 f（x，y，z）、体积元素、三重积分化为柱面坐标 系下形式；
3、过D内任一点（x，y）做平行于z 轴的直线，穿区域确定z的上下限；
利用柱坐标计算三重积分的步骤
考虑是否用柱坐标计算
Ω的投影为圆或圆的一部分 f(x,y,z)中含有x2 y2或arctan y
x
f ( x, y, z)dxdydz
三
变
化为柱坐标系下 三重积分
、 一 勿
积分区域 Ω 被积函数f (x, y, z) 体积元素 dxdydz
忘 一个勿忘
柱坐标表示 f ( cos, sin, z) d d dz
2 z
z 1, 1,
z
上边界: z 2 2 , 下边界: z 2,
原式 =
2π
d
1
d
2 2
zdz
x
0
0
2
o
y
1 2
2
d
0
1(2 2 4)d
0
2
1 4
4
1 6
6
1 0
7 12
.
例4. 计算三重积分
其中 为
由柱面 x2 y2 2x 及平面 z 0, z a (a 0), y 0 所
柱面 与 d;
半平面与 d;
平面z与z dz
在柱面坐标系中体积元素为
d v d dd z
因此
f (x, y, z)dxdydz
z
o
x
dv z dz
z
y
d
d
d d dz
d d d
当积分域的投影域D为与圆域有关的区域时,
一般选用柱面坐标,此时曲面应表示为z z(r, ).
z Dz
2. 对z∈[a,b]用过点(0,0,z)且平行 xOy平面的平面去截Ω ，得截面Dz;
a y
3. 先求关于x,y的二重积分,得
x
F(z) f (x, y, z)dxdy
4. 最后计算单积分
b
a F (z)dz
Dz
第三节
第十章
三重积分
一、三重积分的概念 二、三重积分的计算
2. 利用柱坐标计算三重积分
定限方法：观察、想象．
计算累次积分 注意 对一个变量积分时，将其余变量 视为常数．
小结
三重积分的定义和计算
（计算时将三重积分化为三次积分）
在直角坐标系下的体积元素
dv dxdydz
方法1. “先一后二” 方法2. “先二后一”
dxdy z2 (x,y) f (x, y, z)d z
D
z1(x, y)
b
a d zDZ f (x, y, z)dxdy
先一后二”积分法的基本步骤:
z
1. 把Ω往xoy平面上投影,得积分区域D;
2. 确定上下曲面函数，得 z的积分限;
3. 先求关于z的定积分,得x,y的二元函数;
4. 再求关于x,y的二重积分. “先二后一”积分法的基本步骤:
z
O x
Dxy得z的积分限[a,b];
三
变
化为球坐标系下 三重积分
、 一 勿
积分区域 Ω 被积函数f (x, y, z) 体积元素 dxdydz
忘 一个勿忘 r2 sin
球坐标表示 F (r,, ) r2 sindrdd
化为累次积分
f (r sin sin , r sin cos , r cos )r2 sindrdd
积分次序：一般先r后φ再θ．
如图所示, 在柱面坐标系中体积元素为 z
d v d dd z
z
因此
f (x, y, z)dxdydz
d d dz
dz
O
y
其中
F(, , z) f ( cos , sin , z )
x d
d
d d d
适用范围:
1) 积分域表面用柱面坐标表示时方程简单 ;
2) 被积函数用柱面坐标表示时变量互相分离.
常见曲面的柱面坐标方程
曲面
半球面
圆锥面 旋转抛物面
直角坐标方程 z a2 x2 y2 z x2 y2 z x2 y2
柱面坐标方程 z a2 r2
zr z r2
圆柱面 圆柱面 圆柱面
x2 y2 a2 x2 y2 2ax x2 y2 2ay
ra
r 2a cos r 2asin
4、在 D上分别确定r、上下限（类同于平面极坐标）
柱面坐标常用于：
圆柱体和圆锥体上的三重积分。
例1. 计算三重积分
其中 由抛物面
z x2 y2 与平面 z 4 所围成 .
解: 在xOy面上的投影区域D:
z
上边界曲面为z 4 下边界曲面为z .
4
在柱面坐标系下
原式 =
2π
d
2
d
4
zd z
z
回忆用投影法（先一后二）计算三重积分
f (x, y, z)dV dxdy z2 (x,y) f (x, y, z)dz
D
z1 ( x, y )
O
Dxy
y
x
如果积分区域 在坐标面上的投影区域 D 是圆域
则二重积分应当考虑用极坐标计算.
这就等于用柱面坐标计算三重积分.
2. 利用柱坐标计算三重积分
化为累次积分
f ( cos , sin , z)dddz
积分次序：一般先z后ρ再θ
定限方法：投影、发射
计算累次积分 注意 对一个变量积分时，将其余变量 视为常数
利用球坐标计算三重积分的步骤
考虑是否用球坐标计算
Ω的球或球的一部分 f(x,y,z)中含有x2 y2 z2
f ( x, y, z)dxdydz