当前位置：文档之家 › 极坐标系中二重积分的计算

极坐标系中二重积分的计算

  • 格式：ppt
  • 大小：301.01 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

高等数学：第三讲 极坐标系下二重积分的计算

高等数学：第三讲 极坐标系下二重积分的计算

解：画出积分区域，极点 在区域 D 的外部 区域 D可表示为
D {(r, ) | 2 r 3, 0 2 }
因此Biblioteka ex2y2dxdy 2d
3 er2 rdr
D
0
2
y
2 r 3
4 x2 y2 9
O
x
0 2
例2
2 0
[
1 2
er2
] |32
d
2 ( 1 e9 1 e4 )d
D
o
i1 i
i
r ri1 r ri
x
极坐标系下计算二重积分
再由直角坐标与极坐标的关系
x r cos , y r sin
可得
D f ( x, y)dxdy D f ( x, y)d D f (r cos , r sin )rdrd
D
o
i1
i
r
ri 1
i
r ri
x
极坐标系下计算二重积分
因此
O
x
x2 y2dxdy
d
2sin
r rdr
D
0
0
例3
0
[
1 3
r
3
]
|2sin
0
d
8 sin3 d
30
32 9
y
x2 y2 2y
2 sin
•
0
O
x
谢谢
此时
D f (r cos , r sin )rdrd
r ( )
= d 0 f (r cos , r sin )rdr
r r( )
D
o x
例1
计算
D1
1 x2

利用极坐标系计算二重积分

利用极坐标系计算二重积分
π 2 π 2 a cos θ 0
f ( r , θ)dr ( a ≥ 0).
思考题解答
π π ≤θ≤ D: 2 2 , 0 ≤ r ≤ a cos θ
I = ∫ dr ∫
0 a r arccos a r arccos a
y
θ = arccos
D
r a r = a cosθ
a x
o
f ( r ,θ )dθ .
D
示为极坐标形式的二次积分为______________. 示为极坐标形式的二次积分为______________. 3 、 将 ∫ dx ∫
0 2 3x x
x2
f ( x 2 + y 2 )dy 化为极坐标形式的二
次积分为______________________. 次积分为______________________. 4 、 将 ∫ dx ∫
∫∫ e
D
x2 y2
dxdy = ∫ dθ∫ e
0 0
2π
a
r2
rdr
= π(1 e
a2
).
例3
求广义积分∫0 e
2
∞
x2
dx .
2
解 D1 = {( x , y ) | x + y ≤ R }
2
D2 S
D2 = {( x , y ) | x + y ≤ 2 R }
2 2 2
D1
D S2 D
二、利用极坐标系计算二重积分
∫∫ f ( x , y )dxdy
D
r = ri + ri
θ = θ i + θ i
ηi )xi yi
λ →0 i 1 = n

用极坐标计算二重积分

用极坐标计算二重积分


D
x 2 y 2 4 dxdy
D1 D2
o
2
x

D1

(4 x 2 y 2 )dxdy
2
D2

( x 2 y 2 4)dxdy
3

0 0
d
2
( 4 ) d d
3
2
0 2
3 3
2
( 2 4 ) d
41 2 (4 )d 2 ( 4 )d . 0 2 2


2 3a 1 a . [ sin6 ] 6 0 4 2 6
2

作变换 x u, v , y u, v , 其中 C
1
2 u , v R
,
C
1
,
且
x, y u v 0 u, v u v f x, y d x, y f u , v , u , v u, v dudv

2

例 4．球体 x 2 y 2 z 2 a 2 被圆柱面 x 2 y 2 ax (a 0) 所截得的（含在圆柱面内的部分）立体的体积.
解：由对称性，得
z
x 2 y2 z 2 a 2
V 2

D
a 2 x 2 y 2 dxdy
4
D1

a 2 x 2 y 2 dxdy
2 3
例 2．将二次积分
0 dx 1 x
1
1 x 2
f ( x , y )dy 化为极坐标
下的二次积分.

二重积分的极坐标计算方法

二重积分的极坐标计算方法
⇒ D = { ( r ,θ ) 0 ≤ θ ≤
π
y=x
4
, 0 ≤ r ≤ f (θ ) }
D
1
4
D 由直线 y = x , y = 4 , 及 x = 0 围成的平面区域。 D = D x = { ( x , y ) 0 ≤ x ≤ 4, x ≤ y ≤ 4 }
1 x = 1 ⇒ r cos θ = 1 ⇒ r = ≡ f (θ ) cos θ 1 π ⇒ D = { ( r ,θ ) 0 ≤ θ ≤ , 0 ≤ r ≤ } 4 cos θ
2
7. 用极坐标系下计算二重积分的判断原则 i) 积分区域是圆的一部分或与圆有关； 积分区域是圆的一部分或与圆有关； ii) 被积函数适合在极坐标下的定积分计算（在直角坐标 被积函数适合在极坐标下的定积分计算（ 下的定积分计算不便或根本无法计算）。 下的定积分计算不便或根本无法计算）。
计算二重积分
D = { (r,θ )
( x − 2) 2 + y 2 ≤ 4 }
−
π
-0.5
-1
2 2 (x − 2)2 + y2 = 4 ⇒ (r cosθ − 2)2 + r 2 sin2 θ = 4 2 ⇒ r − 4r cosθ = 0 ⇒ r = 4 cosθ ≡ f (θ ) π π ∴ D = { (r , θ ) − ≤ θ ≤ ，0 ≤ r ≤ 4 cosθ }
2. 二重积分在极坐标系下的形式
∫∫ f ( x, y)dσ = ∫∫ f (r cosθ , r sin θ ) ⋅ r ⋅ drdθ
D D
3. 平面曲线与平面区域在极坐标系下的表示形式
平面曲线的极坐标方程 ：r = g (θ ) , 其中 g 为已知函数。 直角坐标曲线方程转换 为极坐标曲线方程：

在极坐标系下计算二重积分

在极坐标系下计算二重积分

解: (1) 利用对称区间奇偶性，得 I x2dxdy D
Q D x 2d xdy D y 2dyd x
y
I1 (x2y2)dxdy 2D
D o 1x
1 2d 1r3dr
20 0
4
二重积分
综合题： 计算 I (x2xyex2y2)dxdy,其中: D

o
A

D
f
(x,

y)dxdy d
2()f(rcos,
1()
rsin)rdr.
二重积分
例 1 计算 x2 y2 d ， D {( x, y) | 2 x2 y2 4 2}．
D
y
解：D 在极坐标系下可表示为
{ ( r ,) |0 2 , r 2 }
O
x
x2 y2d r rdrd
D
D

2d 2r2dr
0


2
0
r3
(
3
)
|2
d

2 7 3d 1 4 4
03
3
二重积分
例2. 计算 (x2y2)dxdy, 其中D 为由圆 x2 y2 2y, D
x2 y2 4y及直线 y 3x 0, x 3y 0, 所围成的
x
x y
1 x2 y2
是关于Y的奇函数，
D
xy 1x2 y2
dxdy0
D
xy1 1x2 y2
dxdy

D
1 1x2 y2
dxdy
2

2d
0
1r 0 1r2 dr

3_二重积分的计算(极坐标)

3_二重积分的计算(极坐标)
第二节 二重积分的计算
二、利用极坐标计算二重积分
*三、二重积分的换元法
机动
目录
上页
下页
返回
结束
二 极坐标下二重积分的计算
(一)极坐标知识回顾
1定义:在平面取一点O称为原点, 从原点出发作一条射线
称为极轴. 平面上任意点P 与原点距离为 r , 向量O P与极轴为夹角为 , 则点P由数组 , r 唯一确定, 称数组 , r 是点P的极坐标.
例2续计算
其中D 为 1 x 2 y 2 4
y
0 2 解: 在极坐标系下 D : 1 r 2
D3 D1
0
D2
D
x
故
I r rdrd
2 D
D4
d
0
2

2
1
r dr
3
1 4 2 15 2 r |1 2 4
I
D1 D2 D3 D4
. .
D: =1和 =2
围成
: 0 2
0

1
D
2 x
此题用直角系算 麻烦，需使用极 坐标系！
I

D
f ( x , y )dxdy

2π
0
dθ f ( r cosθ , r sin θ )rdr
2 1
机动 目录 上页 下页 返回 结束
例 如图 直线
2 法一 r sin
y2
2
y


r

P , r
l
0
x
法二: 由直线直角坐标方程为 y 2 得 r sin 2 2 故直线极坐标方程为 r 0 sin

经济数学在极坐标系下二重积分的计算

经济数学在极坐标系下二重积分的计算

A
D
( )
d f (r cos ,r sin )rdr.
0
（4）区域如图4
0 2, 0 r ( ).
r ( ) D
o
A
f (r cos ,r sin )rdrd
D
图4
2
( )
d f (r cos ,r sin )rdr.
0
0
如果积分区域D为圆、半圆、圆环、扇形域等， 或被积函数f(x2+y2)形式，利用极坐标常能简化计算.
解 由对称性，可只考虑第一象限部分，
D1
D 4D1
注意：被积函数也要有对称性.
sin( x2 y2 )
dxdy 4
sin( x2 y2 )
dxdy
D
x2 y2
D1
x2 y2
4
2 d
2 sin r
rdr 4.
0
1r
例 5 计算 ( x2 y2 )dxdy，其中 D 为由圆
D
x2 y2 2 y， x2 y2 4 y及直线 x 3y 0，
定r的 上 下 限 ：
任意作过极点的半射线与平面区域相交， 由穿进点，穿出点的极径得到其上下限．
具体地（如图）
（1）区域如图1
r 2()
,
r 1()
D
1( ) r 2( ).
o
A
f (r cos ,r sin )rdrd
图1
D
d
2( ) f (r cos , r sin )rdr.
解 根据对称性有 D 4D1
在极坐标系下
D1
x2 y2 a2 r a,
( x2 y2 )2 2a2( x2 y2 ) r a 2cos2 ,

二重积分的极坐标计算方法

二重积分的极坐标计算方法

sin cos
转换 x , y
r 2 cos2 r 2 sin 2 1 r 1
即此曲线(圆)的极坐标方程为 r g( ) 1 .
例如 : 抛物线 y x2
r sin r2 cos2 r g( ) tan sec
平面区域的极坐标表示形式：
D { ( r, ) , g ( ) r g ( ) }
y
例 计算二重积分 I e xy d ，其中 D 由直线 x = 0 , y = 0 与
x + y = 1 所围成。 D
解：区域 D 如图所示.
y
D
易见，D { (x, y) 0 x 1 , 0 y 1 x }
{ (r, ) 0 , 0 r
1
}
2
sin cos
x
1
y
1
2
无穷条射线（段）束的组合
-2
-1
-1
-2
1
2
-2
1 0.5
2 1.5
1 0.5
-1
1
2
-0.5
0.5
1
1.5
2
-1
0.5 0.4 0.3 0.2 0.1
0.2
0.4
0.6
0.8
1
4 3 2 1
-2 -1
1
2
1 0.8 0.6 0.4 0.2
0.1
0.2
0.3
0.4
0.5
1
yx
D
1
4
D
yx
d d
4a2 x2 y2
0
r
rdr
4a2 r 2
4
2 a sin 0
r 2 asin t

二重积分在极坐标下的计算法

二重积分在极坐标下的计算法

S
14
( 1 eR 2 ) e d (x2 y2 ) ( 1 e2R 2 ).
S
e d 又
(x2 y2 )
S
从而 ( 1 eR 2 )
4
( 1 e2R 2 )
4
令R ,则 ( 1 eR 2 ) , ( 1 e2R 2 ) .
e(x2 y2 )dxdy
R2
( ex2 dx)2
4I 2.
13
作如下三个平面区域
D1 {( x, y) | x2 y2 R2 } D2 {( x, y) | x2 y2 2R2 }
D2
S
DSD1 2
S {(x, y) | R x R, R y R}
D
利用本题结论还可以来推导一个在概率统计中十分有
用的广义积分——Possion积分.
e x2 dx .
0
2
12
ex2 y2 dxdy (1 ea2 ) . e x2 dx .
x2 y2 a2
0
2
解 记 I ex2 dx ,则 0
(2)尽量少分块或不分块.
11
内容回顾
但若被积函数是不可求积函数，则需慎重选择积分 次序,否则将导致无法计算.若不小心选错了积分次序， 则需交换积分次序. 交换积分次序的一般步骤： 1、依据积分限作出积分区域D 的图形. 2、将二次积分转化为二重积分. 3、重新选择积分次序,将二重积分转化为二次积分
1 2
er2
)
a 0
(1 ea2 ) . 11
ex2 y2 dxdy (1 ea2 ) .

极坐标求二重积分公式

极坐标求二重积分公式

极坐标求二重积分公式在数学中，积分（integral）是一种非常重要的操作，它可以用来解决很多复杂的数学问题。

它是采用数学中特定的函数把一个复杂的问题转化为求解单变量函数的问题，从而获得解决方法。

其中，极坐标求二重积分是一个重要的应用，它可以用于计算曲面或者曲线的体积和面积。

极坐标求二重积分是指将极坐标表示的二维函数的计算，例如，在极坐标中表示的二重积分公式：$$ int_0^{2pi} int_0^a f(r, theta) ,dr ,dtheta$$ 其中f(r,θ)是指极坐标下的函数，a是极坐标下的半径。

在极坐标求二重积分之前，我们需要将极坐标表示的函数进行变换，也就是把极坐标下的函数f(r,θ)转换为笛卡尔坐标下的函数g(x,y)。

其中，x = r cosθ，y = r sinθ，我们可以得到下面的变换公式：$$ g(x,y) = f(r, theta)cdot r $$根据这个公式，我们可以得到极坐标求二重积分的公式：$$ int_0^{2pi} int_0^a f(r,theta) cdot r ,dr ,dtheta $$ 该公式代表着从极坐标原点到半径a的圆上的积分，积分面积在极坐标系统中表示为ΔA，则ΔA=πa。

在实际应用中，可以用极坐标求二重积分公式来计算出某个曲面或者曲线上面积的数值。

例如，求解这样一个二重积分问题：设函数z=sinθ,θ介于0到2π，求该曲线上的极坐标下的面积：根据极坐标求二重积分公式，我们可以写出：$$ int_0^{2pi} int_0^1 sin theta cdot r ,dr ,dtheta $$ 由于我们只求解该曲线上的面积，而不是体积，所以半径的上限仍然设定为1，而上限设定为2π。

将上式积分之后，我们可以得到面积的数值：$$ S = int_0^{2pi} int_0^1 sin theta cdot r ,dr ,dtheta = pi$$可见，本题求解结果为π，也就是说，在极坐标下，该曲线的面积为π。

极坐标系下的二重积分计算

极坐标系下的二重积分计算
二、利用极坐标计算二重积分 y
在极坐标系下, 用同心圆 r =常数
及射线 =常数, 分划区域D 为
k (k 1, 2, , n)
o
则除包含边界点的小区域外,小区域的面积
k k
k
k
r rk x
k
1 2
(rk
rk )2 k
1 2
rk
2
k
rk k
rk rk k
在 k 内取点(rk ,k ), 对应有
解
y
3x
0
2
3
x2 y2 4 y r 4sin
x
3y
0
1
6
x2 y2 2 y r 2sin
( x2 y2 )dxdy
3 d
r 4sin 2 rdr 15(
3).
D
6
2sin
2
前页 后页 返回
例 5 计算二重积分 sin( x2 y2 ) dxdy,
D
x2 y2
例7. 求球体
被圆柱面 x2 y2 2 ax
所截得的(含在柱面内的)立体的体积.
解: 设 D : 0 r 2 a cos , 0
2
z
由对称性可知
V 4 D 4 a2 r 2 r d r d
o
y
2 acos 0
4a2 r2 rdr
2a
x
32 a3( 2 )
3 23
前页 后页 返回
设
D
:
1
( )
r
2
(
),
则
r 2 ( )
D
f (r cos , r sin )r d r d
D
d
2 ( )

4 二重积分的计算 极坐标

4 二重积分的计算 极坐标

e
D
x2 y2
dxdy d e
0 0
a2
2
a
r 2
rdr
(1 e
).
高 等 学 校 教 学 课 件
高 等 数 学
例 4
计算
, 其中
是两圆
2 和 x D
之间的环形区域.
解 作 D 的图形(见下图 ),选用极坐标， 它可表示 为 1≤ r ≤ 2 , 0 ≤ ≤ 2 π 于是
高 等 学 校 教 学 课 件
高 等 数 学
例 2
将二重积分 ≤
化为极坐标系下的 ≥ .
累次积分，其中 :
解
画出 D 的图形(见下图), D 可表示为
D
y
r 2Rcos
π 0 ≤ ≤ , 0 ≤ r ≤ 2 R cos , 2 于是得到
f ( x, y)d
D

D
2R

π 2 0
高 等 学 校 教 学 课 件
高 等 数 学
例8
y 计 算 I arctan dxdy x D
D : x 2 y 2 4 , x 2 y 2 1, y x, y 0所围第一象限部分
y
I
y =x

π 4 0
dθ arctantan θ rdr
1
2


π 4 0
D
o
y
2
0
（ 2）
2
A
d 0 f ( r cos , r sin ) r dr .
2
x2 y2 4
2
在极坐标系中，闭区域 D 可表示为
0 ,
D

二重积分在极坐标系下的计算

二重积分在极坐标系下的计算
R
2R
{ x ≥ 0, y ≥ 0}
显然 D1 ⊂ S ⊂ D2
因为 e
所以
− x2 − y2
> 0,
− x2 − y2
∫∫ e D
1
− x2 − y2
dxdy ≤ ∫∫ e
S
dxdy ≤ ∫∫ e
D2
− x2 − y2
dxdy .
又因为 I = ∫∫ e
S
R
− x2 − y2
d xd y
R − y2
计算方法——化为二次积分 化为二次积分 计算方法
D : ρ1 (θ ) ≤ ρ ≤ ρ 2 (θ ), α ≤ θ ≤ β
其中ρ1 (θ ), ρ 2 (θ ) ∈ C [α , β ], 0 ≤ ρ1 (θ ) ≤ ρ 2 (θ ), 0 ≤ β − α ≤ 2 π.
ρ = ρ2(θ)
D
ρ = ρ1(θ) β α
所围成的图形的面积 .
解
根据对称性 S D = 4 S D1 . ( x 2 + y 2 ) 2 = 2a 2 ( x 2 − y 2 ) ⇒ ρ = a 2 cos 2θ
x2 + y2 = a2 ⇒ ρ = a
D1
ρ = a 2 cos 2θ π 得交点 (a , ). 6 ρ = a
S = ∫∫ dxdy = 4 ∫∫ dxdy
θ + dθ
ρdθ
dρ
θ
∆σ ≈ ρdρdθ
ρ ρ + dρ
ρ
dxdy = ρdρdθ
x = ρ cosθ y = ρ sinθ
θ + dθ
二重积分的变量从直角 坐标到极坐标的变换公式

二重积分极坐标计算方法

二重积分极坐标计算方法

二重积分极坐标计算方法
二重积分极坐标是用于求解多变量函数积分问题的一种重要工具。

称为
双重积分，是由两个变量决定的积分，与常规几何坐标内的双重积分不同，
二重积分极坐标完全基于角坐标系中的不同坐标理论，以及它们之间的联系。

在二重积分极坐标中，一个函数的双重积分常用如下的形式来表示：
Integral_θ_θ_θ f(r,θ)rdrdθ
其中，θ是弧度，r表示极坐标中的径向距离，整个积分处理从θ_1,
到θ_2为止，它们是θ的最小最大值。

由于在实际问题中往往存在许多复杂的多变量函数，但应用双重积分极
坐标却可以简化这类问题，从而更好地求解它们。

例如，在双重积分极坐标中，可以利用更大的角度r1与r2来表示一个新的复杂函数，从而简化双重
积分的计算。

此外，双重积分极坐标在力学和电力学计算中也有着广泛的应用，可以
帮助分析物体之间的运动以及电荷场，以及静电场。

因此，双重积分极坐标可以说是一种对解决多变量空间中较复杂的数学
问题有着重要作用的积分方法，它不仅可以帮助我们简化复杂的多变量积分，而且能够帮助我们分析物体间的力学和电力学运动状况。

极坐标系下二重积分的计算

极坐标系下二重积分的计算
所 以 圆 方 程 为 r 1 ,
直 线 方 程 为 rs i n 1 c o,s
x2 y2 1 xy1
f(x, y)dxdyf(rco,srsin)rdrd
D
D
0 2d1 sAi 1 n c ofs(rco,rsi)n rd .11 r
例 3计 算 e x2y2dx， d 其 中 yD是 由 中 心 在 原 点 ，
A
16
I1II2,
( 1 e R 2 ) (R e x 2 d ) 2 x ( 1 e 2 R 2 );
4
0
4
当 R 时 , I1
4
,
I2
4
,
故 当 R 时 ,I ,
4
即( ex2dx)2 ,
0
4
所 求 广 义 积 分ex2dx
.
0
2
A
17
例 6 计算 ( x2 y2 )dxdy，其 D 为由圆
ex2y2dxdy ex2y2dxdy ex2y2dxd.y
D1
S
D2
A
15
又 Ie x 2 y 2 dxdy
S
Rex2dxRey2dy( Rex2dx)2;
0
0
0
I 1 e x 2 y 2 dxdy
D 1
2d
Rer2rdr
(1eR2
);
00
4
同 理 I2 D 2e x 2 y 2 dx 4(d 1ey 2R2 );
D
y 1） 2 x2y24
D o 2x
2）
2
y
2
x2y2 4
D o 2x
3）
2
y
2
x2y24 4）

在极坐标系下二重积分的计算

在极坐标系下二重积分的计算

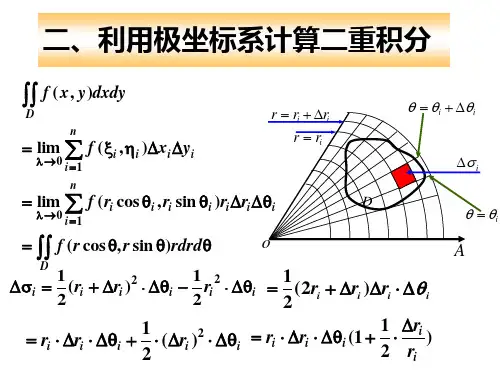
第九节 在极坐标系下二重积分的计算根据微元法可得到极坐标系下的面积微元θσr d r dd = 注意到直角坐标与极坐标之间的转换关系为,c o s θr x = ,sin θr y =从而就得到在直角坐标系与极坐标系下二重积分转换公式为⎰⎰⎰⎰=D D rdrd r r f dxdy y x f θθθ)sin ,cos (),( (9.1)内容分布图示★ 利用极坐标系计算二重积分★ 二重积分化为二次积分的公式★ 例1 ★ 例2 ★ 例3★ 例4 ★ 例5 ★ 例6★ 例7 ★ 例8★ 内容小结 ★ 课堂练习★ 习题6-9★ 返回内容提要：一、二重积分的计算1．如果积分区域D 介于两条射线βθαθ==,之间，而对D 内任一点),(θr ，其极径总是介于曲线)(),(21θϕθϕ==r r 之间（图6-9-2），则区域D 的积分限).()(,21θϕθϕβθα≤≤≤≤r于是 ⎰⎰⎰⎰=D D rdrd r r f dxdy y x f θθθ)sin ,cos (),( .)sin ,cos ()()(21⎰⎰=θϕθϕβαθθθrdr r r f d (9.2)具体计算时，内层积分的上、下限可按如下方式确定：从极点出发在区间),(βα上任意作一条极角为θ的射线穿透区域D （图6-9-2），则进入点与穿出点的极径)(),(21θϕθϕ就分别为内层积分的下限与上限.2．如果积分区域D 是如图6-9-3所示的曲边扇形，则可以把它看作是第一种情形中当)()(,0)(21θϕθϕθϕ==的特例，此时，区域D 的积分限).(0,θϕβθα≤≤≤≤r 于是.)sin ,cos (),()(0⎰⎰⎰⎰=θϕβαθθθrdr r r f d dxdy y x f D (9.3)3．如果积分区域D 如图6-9-4所示，极点位于D 的内部，则可以把它看作是第二种情形中当πβα2,0==的特例，此时，区域D 的积分限).(0,20θϕπθ≤≤≤≤r于是.)sin ,cos (),()(020⎰⎰⎰⎰=θϕπθθθrdr r r f d dxdy y x f D (9.4)注：根据二重积分的性质3，闭区域D 的面积σ在极坐标系下可表示为⎰⎰⎰⎰==DD rdrd d θσσ (9.5) 如果区域D 如图6-9-3所示，则有⎰⎰⎰⎰⎰===βαθϕβαθθϕθθσd rdr d rdrd D )(21)(0 (9.6) 例题选讲：例1（讲义例1）计算⎰⎰++D yx dxdy 221，其中D 是由122≤+y x 所确定的圆域. 例2（讲义例2） 计算⎰⎰++D dxdy y x y x 2222)sin(π, 其中积分区域D 是由4122≤+≤y x 所确定的圆环域.例3（讲义例3）计算⎰⎰D dxdy x y 22, 其中D 是由曲线x y x 222=+所围成的平面区域. 例4（讲义例4）写出在极坐标系下二重积分⎰⎰Ddxdy y x f ),(的二次积分，其中区域}.10,11|),{(2≤≤-≤≤-=x x y x y x D 例5 计算dxdy y x D)(22+⎰⎰,其中D 为由圆y y x y y x 4,22222=+=+及直线03=-y x , 03=-x y 所围成的平面闭区域.例 6 将二重积分σd y x f D⎰⎰),(化为极坐标形式的二次积分,其中D 是曲线,222a y x =+ 42222a y a x =+⎪⎭⎫ ⎝⎛-及直线0=+y x 所围成上半平面的区域.例7（讲义例5）求曲线)(2)(222222y x a y x -=+和a y x ≥+22所围成区域D 的面积.例8（讲义例6）求球体22224a z y x ≤++被圆柱面ax y x 222=+)0(>a 所截得的(含在圆柱面内的部分)立体的体积（图6-9-9）.课堂练习1.计算⎰⎰--D y x dxdy e22, 其中D 是由中心在原点, 半径为a 的圆周所围成的闭区域.2.计算,|2|22⎰⎰-+D d y x σ 其中3:22≤+y x D .。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

D
目录 上一页 下一页 退 出
(3)若极点O在区域D′内，且D′的边界曲线为连续封 闭曲线r=r(θ) (０≤θ≤2π)，如下图所示，则
D （{ r,︱) ０ 2 ,０ r r( )}，
2π
r( )
f (r cos, r sin )rdrd 0 d f (r cos, r sin)rdr
2 32 32
32
3
一般地，当二重积分的积分区域为圆域或圆域一部分，
被积函数为
f ( x 2 ，y 2 ) f或( y ) f等(x形) 式时，用
极坐标计算较方便．
x
y
目录 上一页 下一页 退 出
再根据平面上的点的直角坐标(x,y)与该点的极坐标 (r,θ)之间的关系：
目录 上一页 下一页 退 出
x=rcosθ，y=rsinθ， 得
f (x , y )dσ f (r cos θ,r sin θ)rdrdθ
D
D
其中D′是将D变换成极坐标(r,θ)所对应的区域.
D的三种情形
(1) 若极点O在区域D′之外，且D′由射线θ=α，θ=β和
x
D
D
4π
2cos θ
3 2π
dθ
1
tan θrdr
3
4π 3 2π 3
t
an
θ(
1 2
r
2
2cos 1
θ
)dθ
4π 3 2π 3
t
an
θ(2cos2
θ
1)dθ 2
目录 上一页 下一页 退 出
( 1 cos 2θ 2
1 ln 2
cos θ )
4π 3 2π 3
1 cos 8π 1 cos 4π 1 ln cos 4π 1ln cos 2π 0
)
2 0
d
1 2
2π
(1
e4 )d
π(1
e4 ).
0
目录 上一页 下一页 退 出
例2
计算二重积分
y x
dσ
，其中积分区域
D
D （{ x, y︱)1 x2 y2 2x}.
解 画出积分区域D如下图所示，D用极坐标表示为
D' {(r,︱) 4 ,1 r 2cos}，
3
3
于是
y dσ tan θ r drdθ
§8.3 极坐标系中二重积分的计算
当积分区域为圆或圆的一部分时，用极坐标计算二重 积分可能会比较简单. 如右图所示，设有极坐标系下的积分区 域D，我们用一组以极点为圆心的同心 圆(r =常数)及过极点的一组射线(θ=常 数)将区域D分割成n个小区域．易证得
rr· (r 0， 0)． 从而小区域的面积元素为 d rdrd．
两条连续曲线 则
r r1( ),围r 成r2．(如) 下图所示，
目录 上一页 下一页 退 出
D {(r, ) | , r１( ) r r2 ( )}，

dθ
r2(θ) f (r cos θ,r sin θ)rdr
D
α
r1 (θ)
(2) 若 r1( ) 0，即极点O在区域D′的边界上，且D′由
射线θ=α,θ=β和连续曲线r=r(θ)所围成，如下图所示， 则
D （{ r,｜) ,０ r r( )}，
β
r (θ)
f (r cos θ,r sin θ)rdrdθ α dθθ f (r cos θ,r sin θ)rdr
D'
目录 上一页 下一页 退 出
例1 计算 e y2 x2 dxdy，D为圆x2 y2 4所围成的区域． D
解 积分区域是一个圆域，且
D （{ r,︱) ０ 2 ,０ r 2}，
于是
ey2x2 dxdy
er2 rdrd
2π
d
2 rer2 dr
0
0
D
D'
2π ( 1 er2 02