第二节利用极坐标计算二重积分

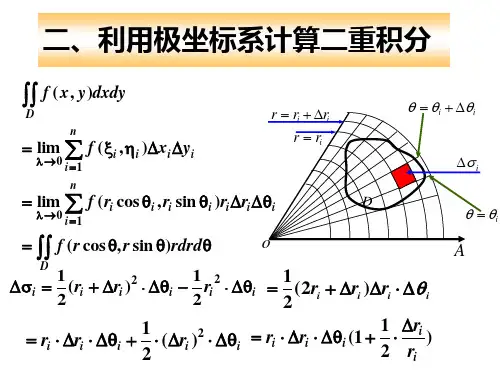
利用极坐标系计算二重积分二重积分可以用极坐标系来计算。

极坐标是一种描述平面上点位置的坐标系统，其中点的位置由距离原点的距离和与正x轴的夹角表示。

极坐标与直角坐标系之间的转换关系如下：x = r * cosθy = r * sinθ其中，x和y是直角坐标系下的坐标，r是点到原点的距离，θ是点与正x轴的夹角。

对于二重积分∬f(x, y)dA，在极坐标下可以表示为∬g(r,θ)rdrdθ，其中，g(r, θ)是将f(x, y)用极坐标来表示。

下面我们将详细介绍如何利用极坐标系计算二重积分。

首先，将被积函数f(x,y)转换为极坐标形式g(r,θ)。

具体来说，我们将x和y替换为r和θ，然后利用极坐标与直角坐标的转换关系，将f(x,y)表示为g(r,θ)。

这个转换过程需要根据具体的被积函数进行分析和计算。

接下来，我们需要确定积分区域。

在极坐标系下，积分区域可以用极坐标表示。

通常情况下，我们将极坐标的范围确定为r的区间[a,b]和θ的区间[α,β]，其中a、b、α和β都是常数。

这样，二重积分就变成了在确定的极坐标区域上的积分。

然后，我们将二重积分∬f(x, y)dA 转换为极坐标下的二重积分∬g(r, θ)rdrdθ。

这个过程需要用到雅可比行列式的公式，即 dA = r dr dθ。

最后，我们按照以下步骤来计算极坐标下的二重积分：1.确定极坐标的范围[a,b]和[α,β]。

2.将被积函数f(x,y)转换为极坐标形式g(r,θ)。

3. 利用雅可比行列式的公式，将二重积分∬f(x, y)dA 转换为∬g(r, θ)rdrdθ。

4.根据极坐标下的积分区域，确定积分范围。

5.将极坐标下的二重积分分解成两个单重积分，先对θ进行积分，再对r进行积分。

6.依次进行积分计算，最后得到结果。

需要注意的是，在进行计算时，要注意被积函数的连续性和积分区域的对称性，以便简化计算。

综上所述，利用极坐标系计算二重积分的步骤包括确定被积函数的极坐标形式、确定积分区域、转换为极坐标下的二重积分、分解为两个单重积分、依次进行积分计算。

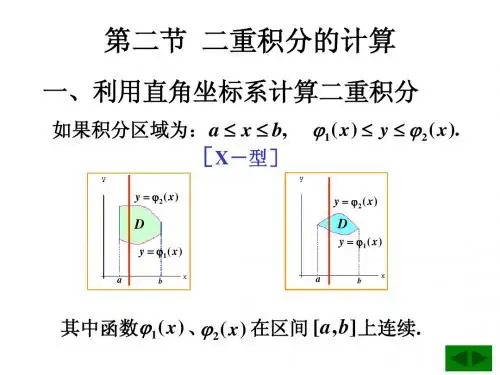
利用极坐标系计算二重积分极坐标系是一种描述平面上点位置的坐标系统，其中每个点由其到原点的距离和与正半轴的夹角来确定。

在极坐标系中，二重积分的计算可以通过转换为极坐标下的积分来简化问题。

假设我们要计算的二重积分为∬Df(x,y)dA，其中D是平面上的一个闭区域，f(x,y)是定义在D上的函数。

首先，我们需要将函数f(x,y)在极坐标下进行表示。

对于任意点(x,y)，其对应的极坐标为(r,θ)，其中r是该点到原点的距离，θ是该点与正半轴的夹角。

根据坐标转换公式，我们可以得到以下关系：x = rcosθy = rsinθ通过对x和y的偏导数运算，我们可以计算出dA在极坐标下的表示：dA = dxdy = rdrdθ将dA代入原积分式，我们可以得到对应的极坐标下的积分：∬D f(x, y) dA = ∬D f(rcosθ, rsinθ) rdrdθ注意到极坐标下的积分中，积分区域D的范围可以通过对r和θ进行适当的取值来表示。

例如，可以通过限定r的范围和θ的范围来确定D的边界。

对于给定的函数f(rcosθ, rsinθ)，我们可以将其在极坐标下展开为级数的形式。

例如，可以将f(rcosθ, rsinθ)展开为幂级数或三角级数的形式，然后通过对级数进行逐项积分来计算二重积分的结果。

在具体计算二重积分时，可以先对θ进行积分，然后再对r进行积分。

具体步骤如下：1.确定积分区域D的边界，即确定r和θ的取值范围。

2. 对θ进行积分，计算出∫f(rcosθ, rsinθ) dr。

3. 对r进行积分，计算出∫∫f(rcosθ, rsinθ) rdrdθ。

4. 根据具体函数f(rcosθ, rsinθ)的形式，可能需要进行级数展开或其他数学方法来计算积分结果。

需要注意的是，在进行极坐标下的二重积分计算时，需要根据具体问题的要求来选择合适的数值计算方法，例如数值积分、级数展开、积分换序等。

总结起来，利用极坐标系计算二重积分的步骤包括确定积分区域D的边界、将函数表示为极坐标下的形式、对θ进行积分、对r进行积分，最后根据具体函数形式计算积分结果。

利用极坐标计算二重积分极坐标是平面直角坐标系的一种描述方式，它采用极径和极角来描述点的位置。

极坐标可以方便地描述圆形和对称图形，因此在解决部分二元函数相关问题时，可以使用极坐标进行计算，本文将探讨如何利用极坐标计算二重积分。

在平面直角坐标系中，二重积分是用来计算平面上某一区域内二元函数的积分值。

在极坐标中，圆形的面积可以被完美地描述为$r^2$，因此二重积分可以用$r$和$\theta$来表示。

在极坐标中，一个二元函数$f(x,y)$可以被表示为：$f(r\cos \theta,r\sin \theta)$。

同样地，二重积分中的区域也可以用$r$和$\theta$的方式表示。

对于一般的二重积分$\iint_D f(x,y)dxdy$，我们可以将其转化为极坐标下的形式：$\iint_D f(r\cos \theta,r\sin\theta)rdrd\theta$。

对于上式中的$rdrd\theta$，在极坐标中可以被理解为区域的微小面积，它由收缩区间$d\theta$和虫蛉区间$dr$构成。

那么一个极坐标下的二重积分应该如何计算呢？下面我们来探讨一下具体步骤：Step1：确定求积区域。

首先需要确定要求的积分区域，根据具体情况，可以使用极坐标方程$r=f(\theta)$或$\theta=g(r)$来表示整个积分区域。

通常情况下，积分区域的形状和对称性都会决定使用哪一个极坐标方程。

Step2：计算微元面积。

在极坐标下，我们需要计算积分区域的微元面积，这个面积由$d\theta$和$dr$构成，可以使用微积分知识来计算。

Step3：建立积分式子。

确定了求积区域并计算微元面积之后，我们可以将积分式子建立起来，这个式子可以根据所求问题来确定。

Step4：推导积分结果。

根据积分式子，我们可以推导出中间的积分结果，这个过程通常需要使用到数学方法和公式，需要耐心和细心地推导。

Step5：计算积分值。

最后，我们需要计算出具体的积分值，这个过程可以使用计算器或者数学软件进行计算，一般需要注意精度和符号问题。