横向双力矩对约束扭转的影响分析

横向荷载下梁的静、动力学特性研究的开题报告一、研究背景和意义梁是结构工程中应用最广泛的一个构件，除受到纵向荷载作用外，还受到横向荷载作用。

横向荷载会引起梁在垂直方向上的挠曲变形和在水平方向上的侧向位移，从而影响梁的静、动力学性能。

因此，研究横向荷载下梁的静、动力学特性，对于工程结构的设计、检验和安全评估具有重要的意义。

二、研究内容和方法本研究将研究横向荷载下梁的静、动力学特性，主要包括以下内容：1. 建立横向荷载下梁的静力学模型，对其进行静力学分析，研究其挠曲变形和侧向位移规律。

2. 建立横向荷载下梁的动力学模型，对其进行动力学分析，研究其动态响应规律。

3. 通过数值仿真，验证静、动力学分析结果的正确性与有效性。

本研究采用数值分析方法进行研究，具体包括有限元法、动力学有限元法等。

三、预期结果和创新点通过本研究，预计能够得到以下结果：1. 确定横向荷载下梁的静、动力学分析方法，为工程实践提供科学的分析手段。

2. 研究横向荷载下梁的静、动力学特性，揭示横向荷载对梁的影响机理，为工程结构设计和安全评估提供参考。

3. 通过数值模拟验证分析结果的正确性与有效性，为工程实践提供可靠的数据支持。

创新点：1. 基于有限元法和动力学有限元法，建立横向荷载下梁的静、动力学模型，分析其静、动力学特性。

2. 探讨横向荷载对梁的静、动力学响应规律，为工程实践提供新的研究思路和设计参考。

3. 结合实际工程，进行数值仿真，验证分析结果的正确性与有效性。

四、研究难点和解决方案研究难点：1. 建立横向荷载下梁的静、动力学模型，考虑多种因素的综合作用。

2. 分析横向荷载下梁的静、动力学特性，揭示其规律性。

3. 通过数值仿真验证分析结果的正确性与有效性。

解决方案：1. 综合考虑梁的几何参数、材料特性、截面形状、荷载形式等因素，建立合理的横向荷载下梁的静、动力学模型。

2. 分析横向荷载下梁的静、动力学特性，采用合适的数值方法，进行详尽的参数敏感性分析和计算实验，深入探讨影响因素，揭示其规律性。

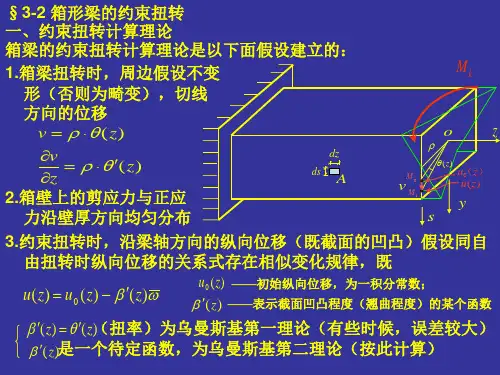
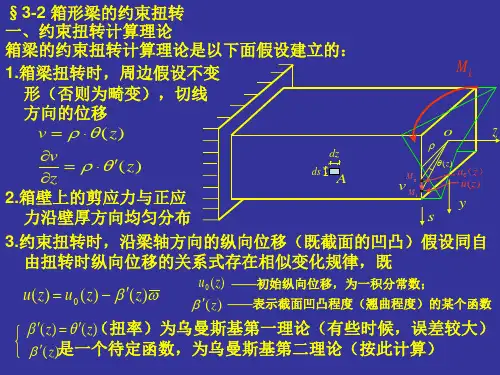
浅析铁路双线箱梁的约束扭转效应研究摘要：初参数法是对约束扭转的常用计算方法，将梁端双力矩、梁端翘曲率、梁端扭率以及梁端扭矩以边界条件计算出来，再构建表达式求出扭转内力，寻找到对箱梁界面最不利的扭转应力。

在了解箱梁约束扭转时，需要注意约束扭转位移模式、约束扭转正应力以及约束扭转剪应力。

在计算箱梁参数对扭转效应时，需要对箱梁参数对扭转效应可能产生的影响进行分析，其中包括翘曲比例系数所受到高跨比的影响、翘曲比例系数所受到壁厚与高宽比的影响、翘曲正应力比所受到悬臂板宽的影响以及剪切比例系数所受到壁厚与高宽比的影响。

关键词：铁路；双线箱梁；约束；扭转引言铁路的双线箱梁拥有抗扭刚度强、形式简洁、受力简单、外形美观以及明确的优点，因此常用与铁路桥梁建设，当双线铁路上运行单线列车，会导致箱梁受到偏心荷载力的作用而发生畸变与扭转，箱梁受到约束扭转所产生的应力影响，需要将其充分地考虑在内，从而确保列车行驶的安全性。

通常会采用有限元法与解析法对约束扭转进行计算，使用初参数法对约束扭转进行计算。

本文针对铁路双线箱梁的约束扭转效应进行研究，现报道如下。

一、箱梁约束扭转初参数法是对约束扭转的常用计算方法，将梁端双力矩、梁端翘曲率、梁端扭率以及梁端扭矩以边界条件计算出来，再构建表达式求出扭转内力，寻找到对箱梁界面最不利的扭转应力。

在了解箱梁约束扭转时，需要注意约束扭转位移模式、约束扭转正应力以及约束扭转剪应力。

1.约束扭转位移模式约束扭转是因为双线铁路承受了单线列车行驶所产生的问题，会出现剪应力与翘曲正应力问题，因此对应力使用自由扭转轴向位移模式进行计算的准确度较低，所以需要在乌曼斯基假定下的约束扭转翘曲位移模式进行计算。

2.约束扭转正应力平衡的弯矩与轴力在箱梁截面翘曲位移中可以帮助约束扭转正应力的计算，计算轴向应力与轴向应变可以通过箱梁截面翘曲位移模式进行计算，再利用平衡的弯矩与轴力和薄壁杆件结构力学计算约束扭转翘曲正应力3.约束扭转剪应力箱壁点平衡方程以弹性力学微元平衡方法构建，结合内外力矩平衡条件计算出约束扭转剪应力。

双力矩作用下薄壁梁变形的数值分析张年文【摘要】By using the solid elements of finite element methods ,the deformations of the cross-sections for thin-walled cantilever beams are analyzed by the application of bimoments at the free end .The numerical results show that :for the open thin-walled beam acted by bi-moment ,the deformation of cross-section is the rotation of the cross -section ,and the relative deformation of the cross -section is very small ,which accords with Vlasov’s rigid contour assumption ,and numerical results agree well with the Vlasov ’s theoretical results .For closed thin-walled cantilever beam acted by bimoments at the free end ,most of the deformation for cross-section is distortion of the cross-section ,and the rotation of cross-section is small ,and the assumption of rigid contour is not true from the numerical results .%采用有限元实体单元，分析了薄壁截面悬臂梁在双力矩作用下的截面内变形。

力矩力对物体旋转运动的影响力矩力是指作用在物体上的一种力，它产生的效果是使物体绕某一轴心发生旋转运动。

力矩力对物体的旋转运动具有显著的影响，本文将就这一主题进行阐述。

下文将从力矩的定义、力矩的计算公式以及力矩对物体旋转的影响三个方面进行论述。

一、力矩的定义力矩是指作用在物体上的力相对于物体某一轴心产生的转动效果。

它是由力的大小、作用点与轴心间的距离来决定的。

力矩的计算需要考虑力的大小和力臂的长度，力臂是指力作用点与轴心的距离垂直于力的方向的长度。

二、力矩的计算公式力矩的计算公式为：力矩 = 力 ×力臂。

其中，力的单位为牛顿（N），力臂的单位为米（m）。

力矩的单位为牛顿米（Nm）或者焦耳（J）。

三、力矩对物体旋转的影响1. 力矩的方向力矩的方向由力的方向和力臂的方向决定。

当力和力臂的方向垂直时，力矩的方向垂直于平面，并且遵循右手定则，即若以右手握住力臂方向，手指指向力的方向，拇指所指的方向即为力矩的方向。

根据力矩的方向不同，物体会产生不同的旋转效果。

2. 力矩的大小力矩的大小由力和力臂的乘积决定。

当力矩的大小越大，物体旋转的加速度也就越大。

3. 力矩的平衡当多个力矩对一个物体产生作用时，如果它们的总和为零，则物体处于力矩平衡状态。

在力矩平衡状态下，物体将保持静止或以匀速旋转。

4. 力矩与转动惯量力矩与物体的转动惯量有密切关系。

转动惯量是指物体抵抗转动运动的能力，它与物体的形状、质量分布以及转动轴的位置有关。

当给定力矩时，物体的转动惯量越大，其旋转加速度就越小，反之亦然。

综上所述，力矩力对物体的旋转运动具有重要的影响。

力矩的计算公式让我们能够量化地描述力矩的大小和方向。

力矩的方向决定了物体的旋转效果，而力矩的大小则决定了物体旋转的加速度。

同时，力矩与转动惯量之间的关系也决定了物体在给定力矩下的旋转速度。

深入理解力矩力对物体旋转运动的影响，对于研究物体的旋转运动以及应用于实际问题具有重要的意义。

横向地震作用下桥梁下部结构的扭转效应罗富元;赫中营;叶爱君【摘要】通过简化的力学模型,进行理论分析,得出在横向地震作用下,桥梁下部结构扭转效应的影响因素.结合一个实际桥梁工程,采用有限元分析方法,针对理论分析所得到的影响因素进行参数分析,得出各影响因素和扭矩的关系.通过两种方法所得结论的相互印证,最终确定扭转效应的影响因素.最后,通过对比计入扭转效应和忽略扭转效应时最不利单桩的受力情况,分析桥梁下部结构的扭转效应对最不利单桩受力的影响.【期刊名称】《结构工程师》【年(卷),期】2015(031)003【总页数】6页(P122-127)【关键词】横向地震作用;桥梁下部结构;扭转效应;最不利单桩【作者】罗富元;赫中营;叶爱君【作者单位】同济大学土木工程防灾国家重点实验室,上海200092;同济大学土木工程防灾国家重点实验室,上海200092;同济大学土木工程防灾国家重点实验室,上海200092【正文语种】中文1 引言由于在桥梁震害调查中，因桥梁下部结构的扭转效应而导致结构破坏的情况很少见，因此，目前针对地震作用下桥梁结构扭转效应的研究很少，而现有的研究对横向地震作用下桥梁下部结构的扭转效应的产生及影响更是没有涉及［1］，此外，现行的《公路桥梁抗震设计细则》(JTG/TB02—01—2008)［2］和《城市桥梁抗震设计规范》(CJJ 166—2011)［3］对于桥梁结构构件抗震验算的规定，也并没有考虑地震作用下产生的扭矩对桥梁结构构件的影响。

对于建筑结构，由于历次震害调查结果表明，建筑结构在地震作用下的扭转效应是造成结构抗震性能退化，导致结构破坏甚至倒塌的重要原因［4］。

所以在《建筑抗震设计规范》(GB 50011—2010)［5］和《高层建筑混凝土结构技术规程》(JGJ 3—2010)［6］中均有关于地震作用下考虑扭转效应的相关规定。

而其中主要考虑的受力构件为刚性楼板下的边缘柱、墙等抗侧力构件。

对于桥梁结构，由于在结构形式上，桥梁的承台和群桩基础的外围单桩与房屋结构的刚性楼板和边缘柱、墙等抗侧力构件有相似性，且群桩基础的外围单桩通常也是桥梁结构在地震作用下的最不利受力单桩［7］，那么，如果在地震作用下桥梁下部结构产生很大的扭转效应，则按照规范而进行的抗震验算，显然会由于忽略扭转效应而存在导致计算结果偏不安全的可能。

车辆横向约束
车辆在⾏驶道路上存在曲率变化较⼤，如果不考虑横向约束执⾏机构转动速率的限制，可能造成车辆转⾓突然变⼤，导致车辆失稳，甚⾄侧翻。

为了保证车辆的横向稳定性需要对横向加以约束[9]。

其中表⽰车辆横向加速度，表⽰车辆速度，表⽰转弯半径，与道路曲率成倒数。

本⽂不考虑车辆纵向控制，设定车辆在⼀定速度下，车道曲
率由车辆传感器给出，所以由式（7）可知当道路曲率变⼤时，车辆加速度会变⼩。

由动⼒学关系求得：
式中为车辆转⾓，L为车辆轴距。

由上⾯两个式⼦知车辆的转⾓可以随道路曲率变化，将作为车辆在道路曲率，速度给定条件下的最⼤转⾓
作为横向约束。