当前位置：文档之家 › 自动控制原理第三章3_劳斯公式

自动控制原理第三章3_劳斯公式

  • 格式：ppt
  • 大小：713.01 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

自动控制原理 第3章-电子素材

自动控制原理 第3章-电子素材

第三章线性系统的时域分析3.1 引言时域法是一种直接在时间域中对系统进行分析的方法。

在输入信号的作用下，系统的输出响应分为动态响应和稳态响应两部分，分别对应动态过程与稳态过程。

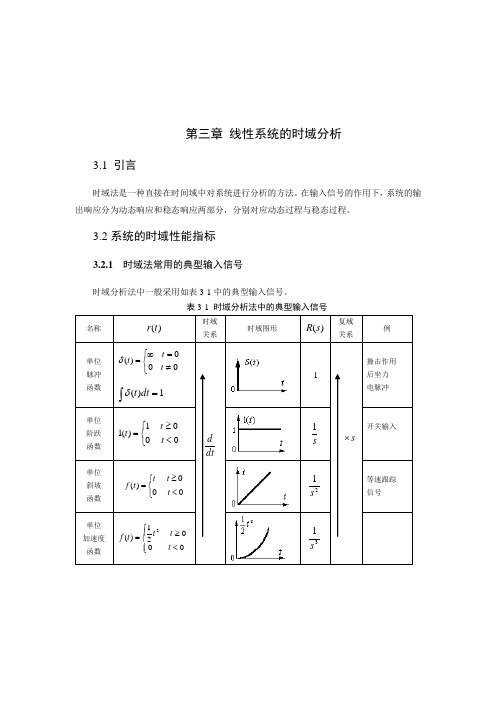
3.2系统的时域性能指标3.2.1时域法常用的典型输入信号时域分析法中一般采用如表3-1中的典型输入信号。

表3-1时域分析法中的典型输入信号3.2.2 系统的时域性能指标系统动态性能是以系统阶跃响应为基础来衡量的。

1. 随动系统的动态性能指标在零初始条件、单位阶跃响应曲线有两种基本形式，如图3-1所示。

为描述曲线的过渡过程，规定以下动态性能指标。

（1）快速性指标①延迟时间d t ：满足()0.5()d h t h =∞时t 的最小正数。

②上升时间r t对于有超调情况如曲线a ，满足()()r h t h =∞时t 的最小正数。

对于无超调情况如曲线b ，响应曲线自开始由稳态值10％上升到稳态值90％所需要的时间。

③峰值时间p t对于曲线a ，响应曲线由开始到第一次达到峰值所需要的时间。

即满足()0pt t dh t dt ==时t 的最小正数。

对于曲线b ，无峰值时间。

④调节时间（过渡过程时间）s t 阶跃响应到达并保持在终值)(∞h 5±％误差带内所需的最短时间(有时取±2％)。

即满足()()5%(2%)()h t h h -∞≤∞或。

（2）平稳性指标（振荡性能、阻尼性能） 描述系统输出跟随给定输入变化时过调或衰减情况。

①超调量%σ峰值)(p t h 超出终值)(∞h 的百分比，即图3-1 随动系统单位阶跃响应曲线%σ()()100%()p h t h h -∞=⨯∞ (3-1)②振荡次数X响应曲线在调节时间内穿过稳态值的次数的一半，称为振荡次数。

平稳性指标只用于有超调时的曲线a ，对于曲线b 则均为0。

对于随动系统,通常只采用调节时间和超调量描述其动态性能。

2. 定值系统的动态性能指标定值系统典型的响应曲线如图3-2所示。

自动控制原理第三章

自动控制原理第三章
1
P75 二阶系统的 结构图
20
2019/4/2
《自动控制原理》第三章
1、无阻尼情况 ( 0)
s 1 ct (t ) L [ 2 ] cos nt t 0 2 s n
等幅振 荡
特征方程有一对共轭虚根 s1,2 jn 2、欠阻尼情况 (0 1)
2019/4/2
《自动控制原理》第三章
7
三.劳斯稳定判据的应用
1、判断系统的稳定性 例: a3 s 3 a2 s 2 a1s a0 0 解:
判断稳定性。
s
3
a3 a2 a1a2 a3 a0 a2 a0
a1 a0 0
0 0
s2 s1 s
0
三阶系统稳定的充要条件是: ai
2019/4/2
瞬态ct (t ) e
ct (t )
t
T
, 稳态css (t ) 1(t )
css (t )
dc(t ) 1 e t /T dt t 0 T
c(t )

t 0
1 T
+
=
2019/4/2
《自动控制原理》第三章
18
二.一阶系统的动态性能指标
c(t )
t 3T
(1 e
t /T
)
t 3T
1 e
3T /T
0.95
T0 T 1 K0
ts 3T
ts 是一阶系统的动态性能指标。
增大系统的开环放大系数K0 会使T 减小，使ts 减小。
2019/4/2
《自动控制原理》第三章
19
第四节
二阶系统的动态性能指标
二阶标准型 或称典型二阶系 统传递函数

自动控制原理及应用课件(第三章)

自动控制原理及应用课件(第三章)

即 s1,2=- n 临界阻尼情况的单位阶跃响应为
C(s) n2 1 (s n )2 s
设部分分式为
C(s) A1 A2 A3
s s n (s n )2
式中，待定系数分别为A1=1，A2=-1，A3=-n
于是有
C(s) 1 1 n s s n (s n )2
取C(s)的拉普拉斯逆变换，则有
R(s) A0 s2
3．抛物线信号 抛物线信号的数学表达式为
0
r(t)
1 2
A0t
2
(t 0) (t ≥ 0)
式中，A0为常数。
当A0=1时，称为单位抛物线信 号，也称为单位加速度信号。
抛物线信号如图所示，它表示
随时间以等加速度增长的信号。
图3-3 抛物线信号
抛物线信号在零初始条件下的拉普拉斯变换为
R(s) A0 s3
4．脉冲信号 脉冲信号是一个脉宽极短的信号，其数学表达式为
0 t < 0；t >
r
(t
)
A0
0<t <
脉冲信号如图3-4（a）所示，
当A0=1时，若令脉宽 →0，则
称为单位理想脉冲函数，记作
(t)，单位脉冲函数如图3-4（
b）所示， (t)函数满足
(t)
0
(t 0) (t 0)
闭环传递函数为 系统特征根为
(s) n2 s2 n2
s1,2 jn
无阻尼情况的单位阶跃响应为
C(s) n2 1 1 s s2 n2 s s s2 n2
取C(s)的拉普拉斯逆变换，则有
c(t) 1 cosnt (t ≥ 0)
系统阶跃响应曲线为等幅振荡，超调量为100％，振荡频率为 自然振荡角频率 n 。由于曲线不收敛，系统处于临界稳定状 态。

自动控制原理第三章习题参考答案

自动控制原理第三章习题参考答案

Y (s) 1 1 600 ( s) 12 （ ） 2 R( s ) s 10 s 60 s 70 s 600
n 600 24.5
70 70 1.43 2 n 2 24 .5
3-7 简化的飞行控制系统结构图如下，试选择参数K1和Kt， 使系统的ωn=6，ξ=1
S2+5=0
S3 16/3 S2 5
S1 10 S0 25
s1, 2 5 j
有1对纯虚根，系统临界稳定。
3-13单位反馈系统的开环传递函数为：
K (0.5s 1) G( s) 2 s( s 1)(0.5s s 1)
确定使系统稳定的K值范围。 解：闭环传递函数为：
K (0.5s 1) ( s) 0.5s 4 1.5s 3 2 s 2 (1 0.5 K ) s K K ( s 2) 4 s 3s 3 4 s 2 ( 2 K ) s 2 K
K 速度误差系数： P lim sG ( s ) 10
s 0
速度误差：
1 e ss 0.1 Kp
3-11 已知系统的特征方程为：
3s 4 10 s 3 5s 2 s 2 0
用劳斯判据确定系统的稳定性 解：列劳斯列表 S4 3 5 2
S3 10
S2 4.7 S1 -3.26
1
2
S0 2 第1列符号变化两次， 说明有两个正根，系统不稳定。
3-12 已知Βιβλιοθήκη 统的特征方程如下，试求系统在S右半平面的根 数及虚根值。
（1） s 3s 12 s 24 s 32 s 48 0
5 4 3 2
S5 1 S4 3 S3 4 S2 12

自动控制原理重要公式

自动控制原理重要公式

0 Z<0A /no 0 t<0At 『200 /<01 2-At 2 f2012 0/ v0A—z、0 t>E 0 / vOA sin ear / > 0B.典型环节的传 礬歎 比例环节G(s) = U 巴=KR ⑶ r z ._c(5) 惯性环节(非周期环节)G(s)= 丽 积分环节G(S)=絆=4R(s) T t s微分环节G(s) = d = 7>R ⑶ 二阶振荡环节(二阶惯性环节)K 咸负&勞闭环传巒数0($)=——= -------- ---R(s) l +G(s)H(s) 正反馈闭环传递函数 0(沪少 34as b3C32A •阶跃函数斜坡函数「(Qi抛物线函数「⑴二正弦函数r(O = %) 2 “ 2 S ++ CO n 延迟环节G(s) =- = e~aR(s)c ・环节间的连接6 a 。

° 0 0 0 。

3 a 2 4 % 0 0a$ d 佝°2 e a o a l■ • °C 6• • • • • a? ■ ■ a2•• ■ •• • •・■ ■■ ■ ■C(y) XM)C(s)_X }(s) X 2(5) ~R U)~ R(S ) x,(5)= G 1(5)G 2(5)--G (5)G ⑶=C(s) _ C,(5)+C 2(s) + • • • + C n (5)串联G(S)=并联反馈R(s) R(s)=G](£)+ G? (s) + …+ G“ (s)开环传递函数=—= G(5)7/(5)E(s)前向通道传递函数二 —=G(5)E(s)d = 6a。

=a \ J 一 6心 A O6OA 3 =d> oa s 6sG($)/?($)1 —G(s)H(s)D ・梅逊增益公式卩=.工空土 F 苗斷驹|抿 A冷斯表中第一列所有元素均大于零aoai bi Cl 32 83b2C2 A = anAg = a a o亠=△ AOflgl hi1~b\ ~ -b、J一 S 劳斯表中某一行的第一个元素为零而该行其它元素不为零，£-0：劳斯表中某一行的元素全为零。

自动控制原理第3章

自动控制原理第3章
本方法是分析系统的最早、也是最基本的分析 方法，时域分析法直覌、物理概念清晰。
2
一、典型的输入信号
1、阶跃信号 数学表达式
r(t) A t 0
拉氏变换式
R(s) A s
当A=1时，称为单位阶跃信号！
r(t) 1
2.斜坡信号 数学表达式
r(t)
R(s) 1 s
At t 0 0 t0
3
典型的输入信号
y(tr ) 1
经整理得
tr
n
1
2
25
二阶系统分析
t tp
2、超调量 ：
暂态过程中被控量的最大值超过稳态值的百分数。
即
%
y(t
P ) y y
100
%
峰值时间 t t p
在 t 时t p刻对 求y导t，令其等于零，经整理得
tp 1 2n
将其代入超调量公式得
% e 1 2 100%
r(t)
A 0t 0 t0 t
拉氏变换式 R(s) A
5
典型的输入信号
当A=1时， 称为单位理想脉冲信号
r(t) (t) R(s) 1
5、正弦信号 数学表达式
r(t) Asin t t 0
拉氏变换式
R(s)
A s2 2
6
二、时域性能指标
以单位阶跃信号输入时，系统输出的一些特征值来表示。
系统对输入信号微分（积分）的响应，就等于该输入 信号响应的微分（积分）。
例3-1(解释)
14
第三节 二阶系统分析 一、二阶系统
用二阶微分方程描述的系统。 二、二阶系统典型的数学模型
先看例：位置跟踪系统
15
二阶系统分析 系统结构图：

自动控制理论第三章第03节分析PPT课件


2012年3月
-9 页/85
机电汽车工程学院
2．＞1（过阻尼）
2
2
2
G ( s ) s 2 2n n s n 2 ( s n ) 2 n (2 1 )n 2 ( s s 1 ) n s (s 2 )
系统闭环极点为： s 1 , 2 n n 2 1 2 1 n
Ri(t)
Ldi(t) dt
uc
ur
ur
i(t) C
uc
uc
1 C
i(t)dt
系统的微分方程为：
LC dd2u 2tcRC ddcutucur
对上式两边做拉氏变换： ( L2 C R s 1 C ) U c ( s ) s U r ( s )
1
G(s)U Ucr((ss))LC 21 sRC 1ss2R Ls C1 L LC
22 1 2 1
2012年3月
-10 页/ 85 1 21e(机2电1 汽)车nt工程学t院0
h (t) c (t) 1
1
1 e (2 1 ) n t
22 1 2 1
响应曲线：
h(t)
1
1 e(21)nt t0
21
>> 1时的近似处理：此时
2 1 2 1
可近似地等效为具有时间常数为 ( 21)n
的传递函数。其实所有的二阶系统的传递函数均可表示为：
G (s)U U c r((s s))s22n n 2 sn2
两系统之间的区别在于， n的两参数的不同。但分母中s
的最高阶次均为2。
典型二阶系统的方框图：
R(s) +
n2
C(s)
ss 2n
典型二阶系统的特征方程为：

自动控制原理(孟华)第3章习题解答

自动控制原理(孟华)第3章习题解答自动控制原理(孟华)的习题答案。

3.1.已知系统的单位阶跃响应为c(t) 1 0.2e 60t 1.2e 10t试求：（1）系统的闭环传递函数Φ(s)=？(2) 阻尼比ζ=？无自然振荡频率ωn=？解：（1）由c(t)得系统的单位脉冲响应为g(t) 12e 60t 12e 10t (t 0)(s) L[g(t)] 12__12 2 s 10s 60s 70s 6002n（2）与标准(s) 2对比得：2s 2 n nn 600 24.5，702 6001.4293.2.设图3.36 (a)所示系统的单位阶跃响应如图3.36 (b)所示。

试确定系统参数K1,K2和a。

(a) (b)图3.36 习题3.2图解：系统的传递函数为K12 nK1K2s(s a)W(s) K2 2 K2 2K1s as K1s 2 n n1s(s a)又由图可知：超调量Mp4 3133峰值时间tp 0.1 s自动控制原理(孟华)的习题答案。

代入得2n K1 1 21e30.1 2 n K K2解得：ln32；0.33，n10 2233.3，K1 n 1108.89，a 2 n 2 0.33 33.3 21.98，K2 K 3。

3.3. 给定典型二阶系统的设计性能指标：超调量p 5%，调节时间ts 3s，峰值时间tp 1s，试确定系统极点配置的区域，以获得预期的响应特性。

解：设该二阶系统的开环传递函数为2nG sss 2 n 20.05 p e33 则满足上述设计性能指标：ts nt 1 p2n得：0.69，n 1 n2由上述各不等式得系统极点配置的区域如下图阴影部分所示：自动控制原理(孟华)的习题答案。

3.4.设一系统如图3.37所示。

(a)求闭环传递函数C(s)/R(s)，并在S平面上画出零极点分布图；(b)当r(t)为单位阶跃函数时，求c(t)并做出c(t)与t的关系曲线。

图3.37 习题3.4图解：(a)系统框图化简之后有C(s)2 s2 R(s)s 0.5s 2.252 s(s35j)(s j)22z1 2,s1,2零极点分布图如下：35j 2自动控制原理(孟华)的习题答案。

自动控制原理参考答案-第3章


×100% = 35%
⇒ ξ = 0.32 ，又 t p =
π
ωn 1 − ξ 2 2 ⇒ K = ωn = 1.96 ； a = 2ξωn = 0.896
= 2.36 ⇒ ωn = 1.4 ；
题 3-5：某速度给定控制系统的动态结构图如题 3-5 图所示。在给定输入量为
r(t) = 10v 直流电压时要求期望的转速输出量为 c(t) = 1000r / min 。试问：稳态反馈
π ωn 1 − ξ
3
2
=
2 3 π = 0.73 ； 15
(∆ = 0.05) 或 ts = 4
ξωn
= 1.2
ξωn
= 1.6
(∆ = 0.02)
题 3-3： 题 3-3 图所示为一位置随动控制系统的动态结构图，输出量为电动机拖
动对象的旋转角度。将速度量反馈回输入端比较环节后构成负反馈内环，速度反 馈系数为τ。试计算：
胡尔维茨行列式 D = 0 5 0 1
10 0 6
0 − 10 10
0 0 0
D2 = 30 D3 = −300 D4 = −1800
0 0 5 0 − 10 D5 = 18000 胡尔维茨行列式非正定，系统不稳定． 题 3-7：已知三个控制系统的特征方程式如下，试应用劳斯稳定判据判定系统 的稳定性；对不稳定的系统要求指出不稳定的极点数；对存在不稳定虚根的要求
4 37
12 K − 40 100 K 70 K − 100
164 K − 1080 100 K 劳斯表： 37 11480 K 2 − 228900 K + 108000 1 s 164 K − 1080 0 s 100 K 若系统稳定则： 164 K − 1080 ⎧ >0 ⎪ 37 ⎪ 2 ⎪11480 K − 228900 K + 108000 >0 ⎨ 164 K − 1080 ⎪ 100 K > 0 ⎪ ⎪ ⎩ ⇒ k > 19.46 题 3-10：已知单位负反馈控制系统的开环传递函数为

自动控制原理第三章3_劳斯公式


3
要使系统稳定，必须 k 0 ①系数皆大于0， ②劳斯阵第一列皆大于0 120 k 0 k 120 有 8 0 k 120 k 0
所以，临界放大系数 k p 120 确定系统的相对稳定性（稳定裕度） 利用劳斯和胡尔维茨稳定性判据确定的是系统稳定或不稳 定，即绝对稳定性。在实际系统中，往往需要知道系统离临界 稳定有多少裕量，这就是相对稳定性或稳定裕量问题。
a3 a2 a2 a1 a3 a0 a2 a0 a1 a0 0 0
s2 s
1
s0
稳定的充要条件为： a3 , a2 , a1 , a0 均大于零
且a1a2 a3a0 0
劳斯判据特殊情况
特殊情况下劳斯阵列的列写及结论： 用一个正数去乘或除某整行，不会改变系统的稳定性结论； 劳斯阵第一列所有系数均不为零，但也不全为正数，则系统不 稳定。表示s右半平面上有极点，极点个数等于劳斯阵列第一列 系数符号改变的次数。 [例]：系统的特征方程为： s 5 2s 4 s 3 3s 2 4s 5 0
现以sx1代入上式得要使系统稳定必须系数皆大于0劳斯阵第一列皆大于018线性系统稳定的充要条件劳斯代数稳定性判据劳斯阵各种特殊情况下劳斯阵的排列和判稳方法劳斯稳定性判据的应用系统参数变化对稳定性的影响系统的相对稳定性
系统的稳定性和代数稳定判据
稳定的充要条件和属性
一、稳定的基本概念和线性系统稳定的充要条件 稳定是控制系统的重要性能，也是系统能够正常运行的首要条 件。控制系统在实际运行过程中，总会受到外界和内部一些因 素的扰动，例如负载和能源的波动、系统参数的变化、环境条 件的改变等。如果系统不稳定，就会在任何微小的扰动作用下 偏离原来的平衡状态，并随时间的推移而发散。因此，如何分 析系统的稳定性并提出保证系统稳定的措施，是自动控制理论 的基本任务之一。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

对于三阶或以上系统，求根是很烦琐的。于是就有了以下 描述的代数稳定性判据。
劳斯判据
二、 劳斯稳定性判据
设线性系统的特征方程为 ansn an1sn1 a1s a0 0 则该 系统稳定的充要条件为： 特征方程的全部系数为正值； 由特征方程系数组成的劳斯阵的第一列也为正。
劳斯表出现零行
设系统特征方程为： ① 有大小相等符号相反的
s4+5s3+7s2+5s+6=0
特征根时会出现零行
劳 s4 1 7 6
② 由零行的上一行构成 辅助方程:
s3 51 51
斯 s2 61 61
s2+1=0
对其求导得零行系数: 2s1
表 s1 02
继续计算劳斯表
s0 1
劳斯表出现零行
1 2
出劳系现斯统零表一何行定时怎会么不出办稳现?定零行?
s2 0( ) 1 0
s1 2 2 0 0 2 2
s0

1
00

令 0则 2 2 故

第一列不全为正，系统不稳
定，s右半平面有两个极点。





2

2,
2

2


1

劳斯判据特殊情况
劳斯阵某行系数全为零的情况。表明特征方程具有大小相等 而位置径向相反的根。至少要下述几种情况之一出现，如：大 小相等，符号相反的一对实根，或一对共轭虚根，或对称于虚 轴的两对共轭复根。
劳斯判据特殊情况
劳斯阵某一行第一项系数为零，而其余系数不全为零。
[处理办法]：用很小的正数 代替零的那一项，然后据此计算出 劳斯阵列中的其他项。若第一次零（即 ）与其上项或下项的
符号相反，计作一次符号变化。
[例]：s4 2s3 s2 2s 1 0
s4 1 1 1
s3 2 2 0
劳斯表第一列元素不变号!
若变号系统不稳定!
变号的次数为特征根在s右半平面的个数!
劳斯判据例子
[例]：特征方程为：a3s3 a2s2 a1s a0 0 ，试判断稳定性。
[解]：劳斯阵为：s3 a3
a1
s 2 a2
a0
s1 a2a1 a3a0 0 a2
s0 a0
0
稳定的充要条件为：
例如: 1 (s2 4)(s2 25)(s 2) s5 2s4 24s3 48s2 25s 50 2 (s2 4)
[处理办法]：可将不为零的最后一行的系数组成辅助方程，对 此辅助方程式对s求导所得方程的系数代替全零的行。大小相等， 位置径向相反的根可以通过求解辅助方程得到。辅助方程应为 偶次数的。
有负实部的共轭复根。或者说，特征方程的根应全部位于s平面 的左半部。
充要条件说明
如果特征方程中有一个正实根，它所对应的指数项将随时 间单调增长；
如果特征方程中有一对实部为正的共轭复根，它的对应项 是发散的周期振荡。
上述两种情况下系统是不稳定的。
如果特征方程中有一个零根，它所对应于一个常数项，系 统可在任何状态下平衡，称为随遇平衡状态；
第一列全大于零,所以系统稳定
设系统特征方程为： 劳斯表介绍
s6+2s5+3s4+4s3+5s2+6s+7=0
s6 1 3
劳
s5 2 s4 1
4 2
57
6
((61-1(064－)-/614=))//-228==1 2
77 劳斯表特点
斯 s3 0ε --88
1 右移一位降两阶
表
ε s2 2ε +8 7ε
s1 -8(2 +8) -7ε 2
a3, a2 , a1, a0 均大于零
且a1a2 a3a0 0
劳斯判据特殊情况
特殊情况下劳斯阵列的列写及结论：
用一个正数去乘或除某整行，不会改变系统的稳定性结论；
劳斯阵第一列所有系数均不为零，但也不全为正数，则系统不 稳定。表示s右半平面上有极点，极点个数等于劳斯阵列第一列 系数符号改变的次数。
点有关，与零点无关。
对于一阶系统，a1s
系统是稳定的。

a0

0, s


a0 a1

,
只要
a0 , a1 都大于零，
对于二阶系统，a2s2 a1s a0 0, s1,2 a1
a12 4a2a0 2a2
只有 a0 , a1, a2 都大于零，系统才稳定。（负实根或实部为负）
系统的稳定性和代数稳定判据
稳定的充要条件和属性
一、稳定的基本概念和线性系统稳定的充要条件
稳定是控制系统的重要性能，也是系统能够正常运行的首要条 件。控制系统在实际运行过程中，总会受到外界和内部一些因 素的扰动，例如负载和能源的波动、系统参数的变化、环境条 件的改变等。如果系统不稳定，就会在任何微小的扰动作用下 偏离原来的平衡状态，并随时间的推移而发散。因此，如何分 析系统的稳定性并提出保证系统稳定的措施，是自动控制理论 的基本任务之一。
如果特征方程中有一对共轭虚根，它的对应于等幅的周期 振荡，称为临界平衡状态（或临界稳定状态）。
从控制工程的角度认为临界稳定状态和随遇平衡状态属于
不稳定。
I m S平面
稳临 定界
不 稳
Re
区稳 定
定区
充要条件说明
注意：稳定性是线性定常系统的一个属性，只与系统本身的结
构参数有关，与输入输出信号无关，与初始条件无关；只与极
2 行列式第一列不动 3 次对角线减主对角线 4 每两行个数相等
s0 7ε
5 分母总是上一行第一个元素
6 一行可同乘以或同除以某正数
7 第一列出现零元素时，
用正无穷小量ε代替。
劳斯判据
系统稳定的必要条件: 特征方程各项系数
均大于零!
有正有负一定不稳定! 缺项一定不稳定!
稳定吗？
系统稳定的充分条件:
[例]：系统的特征方程为： s5 2s4 s3 3s2 4s 5 0
s5 1
1
s4 2
3
s 3 0.5 1.5
s2 9
5
s1 32 0
9
s0 5
0
4
5
0 -1 3 0（ 2）
0
0
1
0
0（
9 32
）
0
劳斯阵第一列有负数， 系统是不稳定的。其 符号变化两次，表示 有两个极点在s的右半 平面。
稳定的基本概念： 设系统处于某一起始的平衡状态。在外作用的影响下，离
开了该平衡状态。当外作用消失后，如果经过足够长的时间它 能回复到原来的起始平衡状态，则称这样的系统为稳定的系统 。 否则为不稳定的系统。
稳定的充要条件和属性
线性系统稳定的充要条件： 系统特征方程的根（即传递函数的极点）全为负实数或具