反比例函数的性质试题汇编

反比例函数的图像与性质训练卷一．选择题（共15小题）1．如图，正比例函数y＝k1x与反比例函数y＝的图象交于A（1，m）、B两点，当k1x ≤时，x的取值范围是（）A．﹣1≤x＜0或x≥1B．x≤﹣1或0＜x≤1C．x≤﹣1或x≥1D．﹣1≤x＜0或0＜x≤12．已知反比例函数y＝（k≠0）的图象经过点（﹣2，4），那么该反比例函数图象也一定经过点（）A．（4，2）B．（1，8）C．（﹣1，8）D．（﹣1，﹣8）3．若点A（﹣2，y1），B（﹣1，y2）都在反比例函数y＝的图象上，则y1，y2的大小关系是（）A．y1＜y2B．y1＝y2C．y1＞y2D．不能确定4．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则一次函数y＝ax+b和反比例函数y＝（c≠0）在同一直角坐标系中的图象可能是（）A．B．C．D．5．如图，等边三角形OAB，点B在x轴正半轴上，S△OAB＝4，若反比例函数y＝（k ≠0）图象的一支经过点A，则k的值是（）A．B．C．D．6．如图，矩形OABC与反比例函数y1＝（k1是非零常数，x＞0）的图象交于点M，N，与反比例函数y2＝（k2是非零常数，x＞0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则k1﹣k2＝（）A．3B．﹣3C．D．7．如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（）A．2B．1C．﹣1D．﹣28．点（1，y1），（2，y2），（3，y3），（4，y4）在反比例函数y＝图象上，则y1，y2，y3，y4中最小的是（）A．y1B．y2C．y3D．y49．如图是同一直角坐标系中函数y1＝2x和y2＝的图象．观察图象可得不等式2x＞的解集为（）A．﹣1＜x＜1B．x＜﹣1或x＞1C．x＜﹣1或0＜x＜1D．﹣1＜x＜0或x＞110．若点A（x1，2），B（x2，﹣1），C（x3，4）都在反比例函数y＝的图象上，则x1，x2，x3的大小关系是（）A．x1＜x2＜x3B．x2＜x3＜x1C．x1＜x3＜x2D．x2＜x1＜x3 11．如图是反比例函数y＝的图象，点A（x，y）是反比例函数图象上任意一点，过点A 作AB⊥x轴于点B，连接OA，则△AOB的面积是（）A．1B．C．2D．12．反比例函数y＝的图象分别位于（）A．第一、第三象限B．第一、第四象限C．第二、第三象限D．第二、第四象限13．一次函数y＝ax+1与反比例函数y＝﹣在同一坐标系中的大致图象是（）A．B．C．D．14．某市举行中学生党史知识竞赛，如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率（该校优秀人数与该校参加竞赛人数的比值）y与该校参加竞赛人数x的情况，其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上，则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是（）A．甲B．乙C．丙D．丁15．已知一次函数y＝kx+b的图象如图所示，则y＝﹣kx+b与y＝的图象为（）A．B．C．D．二．填空题（共8小题）16．如图，反比例函数y＝的图象经过矩形ABCD对角线的交点E和点A，点B、C在x 轴上，△OCE的面积为6，则k＝．17．如图，点P（x，y）在双曲线y＝的图象上，P A⊥x轴，垂足为A，若S△AOP＝2，则该反比例函数的解析式为．18．反比例函数y＝的图象分布情况如图所示，则k的值可以是（写出一个符合条件的k值即可）．19．根据物理学知识，在压力不变的情况下，某物体承受的压强p（Pa）是它的受力面积S （m2）的反比例函数，其函数图象如图所示．当S＝0.25m2时，该物体承受的压强p的值为Pa．20．如图，△OMN是边长为10的等边三角形，反比例函数y＝（x＞0）的图象与边MN、OM分别交于点A、B（点B不与点M重合）．若AB⊥OM于点B，则k的值为．21．在平面直角坐标系xOy中，若反比例函数y＝的图象位于第二、四象限，则k的取值范围是．22．如图，正比例函数y＝k1x和反比例函数y＝图象相交于A、B两点，若点A的坐标是（3，2），则点B的坐标是．23．在反比例函数y＝的图象的每一支曲线上，函数值y随自变量x的增大而增大，则m的取值范围是．三．解答题（共12小题）24．已知反比例函数y＝（k为常数，k≠0）的图象经过点A（﹣2，）．（1）求这个函数的解析式；（2）若点B（m+2，m）在这个函数的图象上，求m的值．25．如图，在平面直角坐标系中，一次函数y1＝kx+b的图象与反比例函数y2＝的图象交于A（4，1），B（﹣2，n）两点，与y轴交于点C．（1）求一次函数与反比例函数的解析式；（2）若点D在y轴上，且S△ABD＝12，求点D的坐标；（3）当y1＞y2时，自变量x的取值范围为．26．如图，一次函数y＝﹣x+3的图象与反比例函数y＝（x＞0）的图象交于A（1，a），B两点，与x轴交于点C．（1）求反比例函数的解析式和点B的坐标；（2）根据图象，直接写出关于x的不等式﹣x+3＜的解集；（3）若点P在x轴上，且S△APC＝5，求点P的坐标．27．已知一次函数y＝kx+b（k≠0）与反比例函数（m≠0）的图象交于A（2，3），B （﹣6，n）两点．（1）求一次函数和反比例函数的解析式；（2）求△AOB的面积．28．如图，一次函数y＝x+5的图象与反比例函数的图象交于A、B两点，其中A（﹣1，a）．（1）求k的值及点B的坐标；（2）请根据图象直接写出不等式的解集．29．如图，一次函数y＝ax+1（a≠0）的图象与x轴交于点A，与反比例函数y＝的图象在第一象限交于点B（1，3），过点B作BC⊥x轴于点C．（1）求一次函数和反比例函数的解析式．（2）求△ABC的面积．30．如图，在平面直角坐标系中，一次函数y＝k1x+b（k1≠0）的图象与反比例函数y＝（k2≠0）的图象相交于A（3，4），B（﹣4，m）两点．（1）求一次函数和反比例函数的解析式；（2）若点D在x轴上，位于原点右侧，且OA＝OD，求△AOD的面积．31．如图，直线AB与反比例函数y＝（k＞0，x＞0）的图象相交于点A和点C（3，2），与x轴的正半轴相交于点B．（1）求k的值；（2）连接OA，OC，若点C为线段AB的中点，求△AOC的面积．32．已知反比例函数y＝（k≠0）的图象的一支如图所示，它经过点（3，﹣2）．（1）求这个反比例函数的表达式，并补画该函数图象的另一支．（2）求当y≤5，且y≠0时自变量x的取值范围．33．如图，点A（m，4）在反比例函数y＝（x＞0）的图象上，点B在y轴上，OB＝2，将线段AB向右下方平移，得到线段CD，此时点C落在反比例函数的图象上，点D落在x轴正半轴上，且OD＝1．（1）点B的坐标为，点D的坐标为，点C的坐标为（用含m的式子表示）；（2）求k的值和直线AC的表达式．34．如图，在平面直角坐标系xOy中，一次函数y＝ax+b（a≠0）的图象与反比例函数y＝（k≠0）的图象交于P、Q两点．点P（﹣4，3），点Q的纵坐标为﹣2．（1）求反比例函数与一次函数的表达式；（2）求△POQ的面积．35．如图，一次函数y＝x+1与反比例函数y＝的图象相交于A（m，2），B两点，分别连接OA，OB．（1）求这个反比例函数的表达式；（2）求△AOB的面积；（3）在平面内是否存在一点P，使以点O，B，A，P为顶点的四边形为平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．。

反比例函数难题汇编及答案解析一、选择题1 .下列函数：①y=-x ； @y=2x ； （3） y = ~— ； （4）y=x 2.当x<0时，y 随x 的增大而减小x的函数有（）A. 1个B. 2个C. 3个D. 4个【答案】B 【解析】 【分析】分别根据一次函数、反比例函数及二次函数的性质进行逐一判断即可. 【详解】一次函数y=-x 中k<0,随x 的增大而减小，故本选项正确；・ ・,正比例函数y=2x 中，k=2,・,•当xVO 时，y 随x 的增大而增大，故本选项错误； ・ ・•反比例函数丁二一^1■中，k= -1V0,・♦.当xVO 时函数的图像在第二象限，此时y 随x 的 增大而增大，故本选项错误；・ ・,二次函数y=x2,中o=1>0,・,•此抛物线开口向上，当xVO 时，y 随x 的增大而减小， 故本选项正确. 故选B. 【点睛】本题考查的是一次函数、反比例函数及二次函数的性质，解题关键是根据题意判断出各函 数的增减性.2.如图，o/WOC 的顶点的坐标分别是4（0,-3）,8 （1, 0）,顶点C,。

在双曲线k y 二一上，边8D 交V 轴于点£,且四边形ACO 石的面积是A45石面积的3倍，则Z 的值x为：（）【答案】A 【解析】A. -6c. -3 D. -12B. -4过D作DF〃>'轴，过C作CE〃x轴，交点为厂，利用平行四边形的性质证明△DCF = AA80,利用平移写好C, D的坐标，由四边形ACDE的面积是AA8E面积的3倍，得到DB = 2BE,利用中点坐标公式求横坐标，再利用反比例函数写。

的坐标，列方程求解女.【详解】解：过D作DF〃y轴，过c作b//x轴，交点为尸，则CF ± DF,:D ABDC,・•・/CDF, /BAO的两边互相平行，AB = DC,.・.ZCDF = NBAO,・・/DFC = 404 = 90。

中考数学试题分类汇总《反比例函数的图象与性质》练习题（含答案）反比例函数的图象与性质1．反比例函数y＝﹣的图象经过点（x1，y1），（x1﹣1，y2），（x1﹣2，y3），其中x1＜0，则（）A．y1＜y2＜y3B．y3＜y2＜y1C．y2＜y1＜y3D．y3＜y1＜y2【分析】根据题意可得x1﹣2＜x1﹣1＜x1＜0，再根据反比例函数增减性即可比较y的大小．【解答】解：∵x1＜0，∴x1﹣1＜0，x1﹣2＜0，且x1﹣2＜x1﹣1＜x1＜0，∵反比例函数y＝﹣的图象经过点（x1，y1），（x1﹣1，y2），（x1﹣2，y3），又∵k＜0时，反比例函数在每一象限内，y随着x增大而增大，∴y3＜y2＜y1，2．已知反比例函数y＝（k是常数，且k≠2）的图象有一支在第三象限，那么k的取值范围是k＞2．【解答】解：∵反比例函数y＝（k是常数，且k≠2）的图象有一支在第三象限，∴k﹣2＞0，解得：k＞2．3．一元二次方程x2+m＝0有两个不相等的实数根，点A（x1，y1）、B（x2，y2）是反比例函数y＝上的两个点，若x1＜x2＜0，则y1＜y2（填“＜”或“＞”或“＝”）．【分析】由一元二次方程根的情况，求得m的值，确定反比例函数y＝图象经过的象限，然后根据反比例函数的性质即可求得结论．【解答】解：∵一元二次方程x2+m＝0有两个不相等的实数根，∴Δ＝0﹣4m＞0，解得m＜0，∵m＜0，∴反比例函数y＝图象在第二、四象限，在每个象限y随x的增大而增大，∵x1＜x2＜0，∴y1＜y2，4．若点A（1，y1），B（2，y2）在反比例函数y＝的图象上，则y1，y2的大小关系是（）A．y2＜0＜y1B．0＜y2＜y1C．y1＜0＜y2D．y1＜y2＜0反比例函数图象上点的坐标特征5．如图，等边△ABO的顶点O与原点重合，点A的坐标是（﹣4，0），点B在第二象限．反比例函数y＝的图象经过点B，则k的值是﹣4．【分析】根据等边三角形的性质结合点A的坐标即可得出点B的坐标，再由点B的坐标利用反比例函数图象上点的坐标特征即可求出k值，此题得解．【解答】解：∵△ABO为等边三角形，且点A的坐标是（﹣4，0），∴点B的坐标为（﹣2，2），∵反比例函数y＝的图象经过点B，∴k＝﹣2×2＝﹣4．6．已知一元二次方程x2﹣4x+m＝0有两个相等的实数根，点A（x1，y1）、B（x2，y2）是反比例函数y＝上的两个点，若x1＞x2＞0，则y1＜y2（填“＜”或“＞”或“＝”）．【解答】解：∵一元二次方程x2﹣4x+m＝0有两个相等的实数根，∴Δ＝16﹣4m＝0，解得m＝4，∵x1＞x2＞0，根据反比例函数的图象，在每一象限内，y的值随着x增大而减小，∴y1＜y2，7．如图，在平面直角坐标系中，点A、B在函数y＝（k＞0，x＞0）的图象上，过点A作x轴的垂线，与函数y＝﹣（x＞0）的图象交于点C，连结BC交x 轴于点D．若点A的横坐标为1，BC＝3BD，则点B的横坐标为（）A．B．2C．D．3【分析】作BE⊥x轴于E，则AC∥BE，即可得到△CDF∽△BDE，由题意得出＝＝，即可得出CF＝2BE，DF＝2DE，设B（，b），则C（1，﹣2b），代入y＝﹣（x＞0）即可求得k＝2b，从而求得B的坐标为2．【解答】解：作BE⊥x轴于E，∴AC∥BE，∴△CDF∽△BDE，∴＝＝，∵BC＝3BD，∴＝＝，∴CF＝2BE，DF＝2DE，设B（，b），∴C（1，﹣2b），∵函数y＝﹣（x＞0）的图象交于点C，∴﹣k＝1×（﹣2b）＝﹣2b，∴k＝2b，∴B的横坐标为＝＝2，8．在平面直角坐标系xOy中，直线y＝kx（k＞0）与双曲线y＝的交于M（x1，y1），N（x2，y2）两点，则x1•y2的值为﹣2．【分析】根据反比例函数和正比例函数均是中心对称图形可知x1＝﹣x2，进一步可知x1•y2的值．【解答】解：∵直线y＝kx（k＞0）与双曲线y＝的交于M（x1，y1），N（x2，y2）两点，∴x1＝﹣x2，x2y2＝2，∴x1•y2＝﹣x2y2＝﹣2．9．若点A（﹣1，a），B（1，b），C（2，c）在反比例函数y＝（k为常数）的图象上，则a，b，c的大小关系是（）A．a＜b＜c B．b＜a＜c C．c＜a＜b D．a＜c＜b【解答】解：∵k2+3＞0，∴反比例函数y＝（k为常数）的图象位于一三象限，且在每个象限内，y 随x的增大而减小，∴点A（﹣1，a）在第三象限，B（1，b），C（2，c）在第一象限，∴a＜0，b＞c＞0，∴a＜c＜b，10．如图，等腰Rt△ABC的斜边AC∥x轴，直角点B落在x轴上，将△ABC向上平移m个单位得到△A′B′C′，点C和点B′恰好在反比例函数y＝（x＞0）的图象上，则m的值是4．【解答】解：设B（a，0），∵等腰Rt△ABC的斜边AC∥x轴，直角点B落在x轴上，∴OA＝OB＝a，AC＝2a，∴C（2a，a），∵△ABC向上平移m个单位得到△A′B′C′，∴B′（a，m），∵点C和点B′恰好在反比例函数y＝（x＞0）的图象上，∴2a•a＝am＝8，解得a＝2，m＝4.11．如图，A，B两点分别在x轴正半轴，y轴正半轴上且∠BAO＝30°，AB＝4，将△AOB沿AB翻折得△ADB，反比例函数y＝（k≠0）的图象恰好经过D点，则k的值是9．【解答】解：∵∠AOB＝90°，∠BAO＝30°，AB＝4，∴AO＝AB cos30°＝4×＝6，∵将△AOB沿AB翻折得△ADB，∴∠DAB＝∠OAB＝30°，AD＝AO＝6，∴∠DAO＝60°，过D作DC⊥OA于C，∴∠ACD＝90°，∴AC＝AD＝3，CD＝AD＝3，∴D（3，3），∵反比例函数y＝（k≠0）的图象恰好经过D点，∴k＝3×3＝9，12．如图，A、B是函数y＝（x＞0）图象上两点，作PB∥y轴，P A∥x轴，PB 与P A交于点P，若S△BOP＝2，则S△ABP＝4．【解答】解：如图，延长BP交x轴于N，延长AP交y轴于M，设点M的纵坐标为m，点N的横坐标为n，∴AM⊥y轴，BN⊥x轴，又∠MON＝90°，∴四边形OMPN是矩形，∵点A，B在双曲线y＝上，∴S△AMO＝S△BNO＝3，∵S△BOP＝2，∴S△PMO＝S△PNO＝1，∴S矩形OMPN＝2，∴mn＝2，∴m＝，∴BP＝|﹣n|＝|3n﹣n|＝2|n|，AP＝|﹣m|＝||，∴S△ABP＝×2|n|×||＝4，13．若A（2，4）与B（﹣2，a）都是反比例函数y＝（k≠0）图象上的点，则a的值是（）A．4B．﹣4C．2D．﹣214．如图，点A是反比例函数y＝（x＜0）的图象上的一点，点B在x轴的负半轴上且AO＝AB，若△ABO的面积为4，则k的值为（）A．2B．4C．﹣2D．﹣4【解答】解：如图，过点A作AD⊥x轴于点D，∵AB＝AO，△ABO的面积为4，∴S△ADO＝|k|＝2，又反比例函数的图象位于第二象限，k＜0，则k＝﹣4．15．如图，A是反比例函数y＝的图象上一点，过点A作AB⊥y轴于点B，点C 在x轴上，且S△ABC＝2，则k的值为（）A．4B．﹣4C．﹣2D．2【分析】先设A点坐标，再根据点A在第二象限，则x＜0，y＞0，然后由三角形面积公式求出xy即可．【解答】解：设点A的坐标为（x，y），∵点A在第二象限，∴x＜0，y＞0，∴S△ABC＝AB•OB＝|x|•|y|＝﹣xy＝2，∴xy＝﹣4，∵A是反比例函数y＝的图象上一点，∴k＝xy＝﹣4，16．如图，在平面直角坐标系中，菱形ABCD的边BC与轴平行，A，B两点纵坐标分别为4，2，反比例函数y＝经过A，B两点，若菱形ABCD边长为4，则k值为（）A．﹣8B．﹣2C．﹣8D．﹣6解：∵四边形ABCD是菱形，∴AB=BC，AD∥BC，+4=4.解得k=±8√3.又∵菱形ABCD边长为4，∴√k216∵函数图象在第二象限，∴k＜0，即k=-8√3.17．如图，A、B是双曲线y＝上的两点，过A点作AC⊥x轴，交OB于点D，垂足为点C，若△ADO的面积为1，D为OB的中点，则k的值为（）A．B．C．3D．4【解答】解：如图，过点B作BE⊥x轴，垂足为E，∵A、B是双曲线y＝上的两点，过A点作AC⊥x轴，∴S△AOC＝S△BOE，∵AC∥BE，∴△OCD∽△OEB，∴＝（）2，又∵D是OB的中点，∴＝，∴＝，∴＝，∴＝，又∵S△AOD＝1，∴S△AOC＝＝|k|，∵k＞0，∴k＝，18．如图，点A在x轴的负半轴上，点C在反比例函数y＝（k＞0）的图象上，AC交y轴于点B，若点B是AC的中点，△AOB的面积为，则k的值为6．【解答】解：如图，过点C作CD⊥y轴于D，∴∠CDB＝∠AOB＝90°，∵点B是AC的中点，∴AB＝CB，在△ABO 和△BCD 中，，∴△CDB ≌△AOB （AAS ），∴BD ＝OB ，∴S △CDB ＝S △AOB ＝S △BCO ＝， ∴S △COD ＝3，∴|k |＝S △COD ＝3，∴|k |＝6，∵k ＞0，∴k ＝6．19．如图，点A 是反比例函数y ＝（k ≠0，x ＜0）图象上的一点，经过点A 的直线与坐标轴分别交于点C 和点D ，过点A 作AB ⊥y 轴于点B ，＝，连接BC ，若△BCD 的面积为2，则k 的值为﹣6 ． 【解答】解：连接OA ，如图所示：∵＝，△BCD 的面积为2，∴△COD 的面积为4，∵AB ⊥y 轴，∴AB ∥OC ，∴△ABD ∽△COD ，∴＝（）2＝，∴S △ABD ＝1， ∵＝，∴S △AOD ＝2，∴S △AOB ＝3，∵S △ABO ＝|k |，∴|k |＝3，∴|k |＝6，根据图象可知，k ＜0，∴k ＝﹣6．20．如图，P为反比例函数图象上一点，以点P为圆心的⊙P与两坐标轴都相切，点E为y轴负半轴上一点，过点P作PF⊥PE交x轴于F，若OF ﹣OE＝8，则k＝16．【分析】过P点作x轴、y轴的垂线，垂足为A、B，根据⊙P与两坐标轴都相切可知，P A＝PB，由∠APB＝∠EPF＝90°可证△BPE≌△APF，得BE＝AF，利用OF﹣OE＝8，求圆的半径，根据k＝OA•P A求解．【解答】解：如图，过P点作x轴、y轴的垂线，垂足为A、B，∵⊙P与两坐标轴都相切，∴P A＝PB，四边形OAPB为正方形，∵∠APB＝∠EPF＝90°，∴∠BPE＝∠APF，∴Rt△BPE≌Rt△APF，∴BE＝AF，∵OF﹣OE＝8，∴（OA+AF）﹣（BE﹣OB）＝8，即2OA＝8，解得OA＝4，∴k＝OA•P A＝4×4＝16．20．如图，点A是函数y＝（x＞0）的图象上任意一点，AB∥x轴交函数y＝（x＜0）的图象于点B，以AB为边作平行四边形ABCD，且S▱ABCD＝5，C、D 在x轴上，则k＝﹣3．【解答】解：设点A（x，），则B（，），∴AB＝x﹣，则（x﹣）＝5，k＝﹣3．21．如图，反比例函数的图象经过菱形OABD的顶点A和边BD 的一点C，且，若点D的坐标为（8，0），则k的值为3．【解答】解：作AE⊥x轴于E，CF⊥x轴于F，∵四边形OABD是菱形，点D的坐标为（8，0），∴OA∥BD，OA＝BD＝8，∴∠AOE＝∠CDF，∵∠AEO＝∠CFD＝90°，∴△AOE∽△CDF，∴＝＝，∵，∴＝＝＝3，∴OE＝3DF，AE＝3CF，设DF＝m，CF＝n，则C（8+m，n），A（3m，3n），∵点A、C在反比例函数的图象上，∴（8+m）•n＝3m•3n，∴m＝1，∴A（3，3n），∴OE＝3，AE＝3n，在Rt△AOE中，OA2＝OE2+AE2，∴82＝32+（3n）2，解得n＝，∴A（3，），∴k＝3×＝3，22．如图，在平面直角坐标系中，将直线y＝﹣3x向上平移3个单位，与y轴、x轴分别交于点A、B，以线段AB为斜边在第一象限内作等腰直角三角形ABC．若反比例函数（x＞0）的图象经过点C，则k的值为4．【解答】解：过点C作CE⊥x轴于点E，作CF⊥y轴于点F，如图所示．∵CE⊥x轴，CF⊥y轴，∴∠ECF＝90°．∵△ABC为等腰直角三角形，∴∠ACF+∠FCB＝∠FCB+∠BCE＝90°，AC＝BC，∴∠ACF＝∠BCE．在△ACF和△BCE中，，∴△ACF≌△BCE（AAS），∴S△ACF＝S△BCE，∴S矩形OECF＝S四边形OBCA＝S△AOB+S△ABC．∵将直线y＝﹣3x向上平移3个单位可得出直线AB，∴直线AB的表达式为y＝﹣3x+3，∴点A（0，3），点B（1，0），∴AB＝＝，∵△ABC为等腰直角三角形，∴AC＝BC＝，∴S矩形OECF＝S△AOB+S△ABC＝×1×3+××＝4．∵反比例函数y＝（x＞0）的图象经过点C，∴k＝4，反比例函数与一次函数的交点问题23．反比例函数y＝与一次函数y＝kx+b的交点的纵坐标如图所示，则不等式＞kx+b的解集是（）A．x＜﹣1或0＜x＜2B．x＜﹣2或0＜x＜1C．﹣1＜x＜0或x＞2D．﹣2＜x＜0或x＞1【解答】解：根据图象可知，反比例函数y＝与一次函数y＝kx+b的交点的纵坐标分别为1，﹣2，将交点纵坐标分别代入反比例函数解析式，得交点横坐标分别为2，﹣1，∴不等式＞kx+b的解集是x＜﹣1或0＜x＜2，。

三年（2021-2023）中考数学真题分项汇编【全国通用】专题12反比例函数的图象与性质（优选真题60道）一．选择题（共20小题）1．（2023•通辽）已知点A（x1，y1）B（x2，y2）在反比例函数y=−2x的图象上，且x1＜0＜x2，则下列结论一定正确的是（）A．y1+y2＜0B．y1+y2＞0C．y1﹣y2＜0D．y1﹣y2＞02．（2023•湖北）在反比例函数y=4−kx的图象上有两点A（x1，y1），B（x2，y2），当x1＜0＜x2时，有y1＜y2，则k的取值范围是（）A．k＜0B．k＞0C．k＜4D．k＞43．（2023•武汉）关于反比例函数y=3x，下列结论正确的是（）A．图象位于第二、四象限B．图象与坐标轴有公共点C．图象所在的每一个象限内，y随x的增大而减小D．图象经过点（a，a+2），则a＝14．（2023•永州）已知点M（2，a）在反比例函数y=kx的图象上，其中a，k为常数，且k＞0，则点M一定在（）A．第一象限B．第二象限C．第三象限D．第四象限5．（2023•天津）若点A（x1，﹣2），B（x2，1），C（x3，2）都在反比例函数y=−2x的图象上，则x1，x2，x3的大小关系是（）A．x3＜x2＜x1B．x2＜x1＜x3C．x1＜x3＜x2D．x2＜x3＜x16．（2023•邵阳）如图，矩形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=kx（k≠0）的图象上，点B的坐标为（2，4），则点E的坐标为（）A．（4，4）B．（2，2）C．（2，4）D．（4，2）7．（2023•上海）下列函数中，函数值y随x的增大而减小的是（）A．y＝6x B．y＝﹣6x C．y=6x D．y=−6x8．（2023•金华）如图，一次函数y＝ax+b的图象与反比例函数y=kx的图象交于点A（2，3），B（m，﹣2），则不等式ax+b＞kx的解是（）A．﹣3＜x＜0或x＞2B．x＜﹣3或0＜x＜2 C．﹣2＜x＜0或x＞2D．﹣3＜x＜0或x＞39．（2023•山西）若点A（﹣3，a），B（﹣1，b），C（2，c）都在反比例函数y=kx(k＜0)的图象上，则a，b，c的大小关系用“＜”连接的结果为（）A．b＜a＜c B．c＜b＜a C．a＜b＜c D．c＜a＜b10．（2023•株洲）下列哪个点在反比例函数y=4x的图象上？（）A．P1（1，﹣4）B．P2（4，﹣1）C．P3（2，4）D．P4(2√2，√2) 11．（2023•临沂）正在建设中的临滕高速是我省“十四五”重点建设项目．一段工程施工需要运送土石方总量为105m3，设土石方日平均运送量为V（单位：m3/天），完成运送任务所需要的时间为t（单位：天），则V与t满足（）A．反比例函数关系B．正比例函数关系C．一次函数关系D．二次函数关系12．（2023•宁波）如图，一次函数y1＝k1x+b（k1＞0）的图象与反比例函数y2=k2x（k2＞0）的图象相交于A，B两点，点A的横坐标为1，点B的横坐标为﹣2，当y1＜y2时，x的取值范围是（）A ．x ＜﹣2或x ＞1B ．x ＜﹣2或0＜x ＜1C ．﹣2＜x ＜0或x ＞1D ．﹣2＜x ＜0或0＜x ＜113．（2023•浙江）已知点A （﹣2，y 1），B （﹣1，y 2），C （1，y 3）均在反比例函数y =3x的图象上，则y 1，y 2，y 3的大小关系是（ ） A ．y 1＜y 2＜y 3B ．y 2＜y 1＜y 3C ．y 3＜y 1＜y 2D ．y 3＜y 2＜y 114．（2023•云南）若点A （1，3）是反比例函数y =kx （k ≠0）图象上一点，则常数k 的值为（ ） A ．3B ．﹣3C ．32D ．−3215．（2022•贵阳）如图，在平面直角坐标系中有P ，Q ，M ，N 四个点，其中恰有三点在反比例函数y =kx （k ＞0）的图象上．根据图中四点的位置，判断这四个点中不在函数y =kx的图象上的点是（ ）A ．点PB ．点QC ．点MD ．点N16．（2022•无锡）已知一次函数y ＝x +2的图象上存在两个点，这两个点关于y 轴的对称点恰好在反比例函数y =kx （k ＞0）的图象上，则k 的范围是（ ） A ．0＜k ＜12B ．0＜k ＜1C ．0＜k ＜2D ．0＜k ＜417．（2022•邵阳）如图是反比例函数y =1x 的图象，点A （x ，y ）是反比例函数图象上任意一点，过点A 作AB ⊥x 轴于点B ，连接OA ，则△AOB 的面积是（ ）A ．1B ．12C ．2D ．3218．（2022•东营）如图，一次函数y 1＝k 1x +b 与反比例函数y 2=k2x 的图象相交于A ，B 两点，点A 的横坐标为2，点B 的横坐标为﹣1，则不等式k 1x +b ＜k2x 的解集是（ ）A ．﹣1＜x ＜0或x ＞2B ．x ＜﹣1或0＜x ＜2C ．x ＜﹣1或x ＞2D ．﹣1＜x ＜219．（2021•荆门）在同一平面直角坐标系中，函数y ＝kx ﹣k 与y =k|x|（k ≠0）的大致图象是（ ）A．①②B．②③C．②④D．③④20．（2021•荆州）已知：如图，直线y1＝kx+1与双曲线y2=2x在第一象限交于点P（1，t），与x轴、y轴分别交于A，B两点，则下列结论错误的是（）A．t＝2B．△AOB是等腰直角三角形C．k＝1D．当x＞1时，y2＞y1二．填空题（共20小题）21．（2023•河北）如图，已知点A（3，3），B（3，1），反比例函数y=kx(k≠0)图象的一支与线段AB有交点，写出一个符合条件的k的整数值：．22．（2023•陕西）如图，在矩形OABC和正方形CDEF中，点A在y轴正半轴上，点C，F均在x轴正半轴上，点D在边BC上，BC＝2CD，AB＝3．若点B，E在同一个反比例函数的图象上，则这个反比例函数的表达式是．23．（2023•荆州）如图，点A（2，2）在双曲线y=kx（x＞0）上，将直线OA向上平移若干个单位长度交y轴于点B，交双曲线于点C．若BC＝2，则点C的坐标是．24．（2023•鄂州）如图，在平面直角坐标系中，直线y1＝k1x+b与双曲线y2=k2x（其中k1•k2≠0）相交于A（﹣2，3），B（m，﹣2）两点，过点B作BP∥x轴，交y轴于点P，则△ABP的面积是．25．（2023•无锡）已知曲线C1、C2分别是函数y=−2x（x＜0），y=kx（k＞0，x＞0）的图象，边长为6的正△ABC的顶点A在y轴正半轴上，顶点B、C在x轴上（B在C的左侧），现将△ABC绕原点O顺时针旋转，当点B在曲线C1上时，点A恰好在曲线C2上，则k的值为．26．（2023•徐州）如图，点P在反比例函数y=kx(k＞0)的图象上，P A⊥x轴于点A，PB⊥y轴于点B，P A＝PB．一次函数y＝x+1的图象与PB交于点D，若D为PB的中点，则k的值为．27．（2023•上海）函数f（x）=1x−23的定义域为．28．（2023•内江）如图，在平面直角坐标系中，O为坐标原点，MN垂直于x轴，以MN为对称轴作△ODE的轴对称图形，对称轴MN与线段DE相交于点F，点D的对应点B恰好落在反比例函数y=kx（x＜0）的图象上，点O、E的对应点分别是点C、A，若点A为OE的中点，且S△EAF=14，则k的值为．29．（2023•安徽）如图，O是坐标原点，Rt△OAB的直角顶点A在x轴的正半轴上，AB＝2，∠AOB＝30°，反比例函数y=kx（k＞0）的图象经过斜边OB的中点C．（1）k＝；（2）D为该反比例函数图象上的一点，若DB∥AC，则OB2﹣BD2的值为．30．（2023•枣庄）如图，在反比例函数y=8x（x＞0）的图象上有P1，P2，P3，…P2024等点，它们的横坐标依次为1，2，3，…，2024，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3，…，S2023，则S1+S2+S3+…+S2023＝．31．（2023•乐山）定义：若x，y满足x2＝4y+t，y2＝4x+t且x≠y（t为常数），则称点M（x，y）为“和谐点”．（1）若P（3，m）是“和谐点”，则m＝；（2）若双曲线y=kx（﹣3＜x＜﹣1）存在“和谐点”，则k的取值范围．32．（2023•连云港）如图，矩形OABC的顶点A在反比例函数y=kx（x＜0）的图象上，顶点B、C在第一象限，对角线AC∥x轴，交y轴于点D．若矩形OABC的面积是6，cos∠OAC=23，则k＝．33．（2022•乐山）如图，平行四边形ABCD的顶点A在x轴上，点D在y=kx（k＞0）上，且AD⊥x轴，CA的延长线交y轴于点E．若S△ABE=32，则k＝．34．（2022•北京）在平面直角坐标系xOy中，若点A（2，y1），B（5，y2）在反比例函数y=kx（k＞0）的图象上，则y1y2（填“＞”“＝”或“＜”）．35．（2022•包头）如图，反比例函数y=kx（k＞0）在第一象限的图象上有A（1，6），B（3，b）两点，直线AB与x轴相交于点C，D是线段OA上一点．若AD•BC＝AB•DO，连接CD，记△ADC，△DOC的面积分别为S1，S2，则S1﹣S2的值为．36．（2022•湖州）如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，tan∠ABO＝3，以AB为边向上作正方形ABCD．若图象经过点C的反比例函数的解析式是y=1x，则图象经过点D的反比例函数的解析式是．37．（2021•呼和浩特）正比例函数y＝k1x与反比例函数y=k2x的图象交于A，B两点，若A点坐标为（√3，﹣2√3），则k1+k2＝．38．（2021•阿坝州）如图，点A，B在反比例函数y=kx（k＞0）的图象上，点A的横坐标为2，点B的纵坐标为1，OA⊥AB，则k的值为．39．（2021•荆门）如图，在平面直角坐标系中，Rt△OAB斜边上的高为1，∠AOB＝30°，将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD，点A的对应点C恰好在函数y=kx（k≠0）的图象上，若在y=kx的图象上另有一点M使得∠MOC＝30°，则点M的坐标为．40．（2021•通辽）如图，△OA1B1，△A1A2B2，△A2A3B3，…，△A n﹣1A n B n都是斜边在x轴上的等腰直角三角形，点A1，A2，A3，…，A n都在x轴上，点B1，B2，B3，…，B n都在反比例函数y=1x（x＞0）的图象上，则点B n的坐标为．（用含有正整数n的式子表示）三．解答题（共20小题）41．（2023•兰州）如图，反比例函数y=kx(x＜0)与一次函数y＝﹣2x+m的图象交于点A（﹣1，4），BC⊥y轴于点D，分别交反比例函数与一次函数的图象于点B，C．（1）求反比例函数y=kx与一次函数y＝﹣2x+m的表达式；（2）当OD＝1时，求线段BC的长．42．（2023•常德）如图所示，一次函数y1＝﹣x+m与反比例函数y2=kx相交于点A和点B（3，﹣1）．（1）求m的值和反比例函数解析式；（2）当y1＞y2时，求x的取值范围．43．（2023•贵州）如图，在平面直角坐标系中，四边形OABC是矩形，反比例函数y=kx(x＞0)的图象分别与AB，BC交于点D（4，1）和点E，且点D为AB的中点．（1）求反比例函数的表达式和点E的坐标；（2）若一次函数y＝x+m与反比例函数y=kx(x＞0)的图象相交于点M，当点M在反比例函数图象上D，E之间的部分时（点M可与点D，E重合），直接写出m的取值范围．44．（2023•湘潭）如图，点A 的坐标是（﹣3，0），点B 的坐标是（0，4），点C 为OB 中点．将△ABC 绕着点B 逆时针旋转90°得到△A ′BC ′．（1）反比例函数y =kx的图象经过点C ′，求该反比例函数的表达式； （2）一次函数图象经过A 、A ′两点，求该一次函数的表达式．45．（2023•东营）如图，在平面直角坐标系中，一次函数y ＝ax +b （a ＜0）与反比例函数y =kx （k ≠0）交于A （﹣m ，3m ），B （4，﹣3）两点，与y 轴交于点C ，连接OA ，OB ． （1）求反比例函数和一次函数的表达式； （2）求△AOB 的面积；（3）请根据图象直接写出不等式kx ＜ax +b 的解集．46．（2023•菏泽）如图，已知坐标轴上两点A （0，4），B （2，0），连接AB ，过点B 作BC ⊥AB ，交反比例函数y =kx 在第一象限的图象于点C （a ，1）．（1）求反比例函数y =k x和直线OC 的表达式；（2）将直线OC 向上平移32个单位，得到直线l ，求直线l 与反比例函数图象的交点坐标．47．（2023•济宁）如图，正比例函数y 1=12x 和反比例函数y 2=kx (x ＞0)的图象交于点A （m ，2）． （1）求反比例函数的解析式；（2）将直线OA 向上平移3个单位后，与y 轴交于点B ，与y 2=kx(x ＞0)的图象交于点C ，连接AB ，AC ，求△ABC 的面积．48．（2023•河南）小军借助反比例函数图象设计“鱼形”图案，如图，在平面直角坐标系中，以反比例函数y =kx 图象上的点A(√3，1) 和点B 为顶点，分别作菱形AOCD 和菱形OBEF ，点D ，E 在x 轴上，以点O 为圆心，OA 长为半径作AC ̂，连接BF ． （1）求k 的值；（2）求扇形AOC 的半径及圆心角的度数； （3）请直接写出图中阴影部分面积之和．49．（2023•聊城）如图，一次函数y＝kx+b的图象与反比例函数y=mx的图象相交于A（﹣1，4），B（a，﹣1）两点．（1）求反比例函数和一次函数的表达式；（2）点p（n，0）在x轴负半轴上，连接AP，过点B作BQ∥AP，交y=mx的图象于点Q，连接PQ．当BQ＝AP时，若四边形APQB的面积为36，求n的值．50．（2023•岳阳）如图，反比例函数y=kx（k为常数，k≠0）与正比例函数y＝mx（m为常数，m≠0）的图象交于A（1，2），B两点．（1）求反比例函数和正比例函数的表达式；（2）若y轴上有一点C（0，n），△ABC的面积为4，求点C的坐标．51．（2023•滨州）如图，直线y＝kx+b（k，b为常数）与双曲线y=mx(m为常数）相交于A（2，a），B（﹣1，2）两点．（1）求直线y＝kx+b的解析式；（2）在双曲线y=mx上任取两点M（x1，y1）和N（x2，y2），若x1＜x2，试确定y1和y2的大小关系，并写出判断过程；（3）请直接写出关于x的不等式kx+b＞mx的解集．52．（2023•十堰）函数y=kx+a的图象可以由函数y=kx的图象左右平移得到．（1）将函数y=1x的图象向右平移4个单位得到函数y=1x+a的图象，则a＝；（2）下列关于函数y=1x+a的性质：①图象关于点（﹣a，0）对称；②y随x的增大而减小；③图象关于直线y＝﹣x+a对称；④y的取值范围为y≠0．其中说法正确的是（填写序号）；（3）根据（1）中a的值，写出不等式1x+a ＞1x的解集．53．（2023•湖北）如图，一次函数y1＝kx+b（k≠0）与函数为y2=mx(x＞0)的图象交于A(4，1)，B(12，a)两点．（1）求这两个函数的解析式；（2）根据图象，直接写出满足y1﹣y2＞0时x的取值范围；（3）点P在线段AB上，过点P作x轴的垂线，垂足为M，交函数y2的图象于点Q，若△POQ面积为3，求点P的坐标．54．（2023•内江）如图，在平面直角坐标系中，一次函数y＝mx+n与反比例函数y=kx的图象在第一象限内交于A（a，4）和B（4，2）两点，直线AB与x轴相交于点C，连接OA．（1）求一次函数与反比例函数的表达式；（2）当x＞0时，请结合函数图象，直接写出关于x的不等式mx+n≥kx的解集；（3）过点B作BD平行于x轴，交OA于点D，求梯形OCBD的面积．55．（2023•衡阳）如图，正比例函数y=43x的图象与反比例函数y=12x（x＞0）的图象相交于点A．（1）求点A的坐标．（2）分别以点O、A为圆心，大于OA一半的长为半径作圆弧，两弧相交于点B和点C，作直线BC，交x轴于点D．求线段OD的长．56．（2023•株洲）如图所示，在平面直角坐标系Oxy中，四边形OABC为正方形，其中点A、C分别在x轴负半轴，y轴负半轴上，点B在第三象限内，点A（t，0），点P（1，2）在函数y=kx(k＞0，x＞0)的图象上．（1）求k的值；（2）连接BP、CP，记△BCP的面积为S，设T＝2S﹣2t2，求T的最大值．57．（2022•营口）如图，在平面直角坐标系中，△OAC的边OC在y轴上，反比例函数y=kx（x＞0）的图象经过点A和点B（2，6），且点B为AC的中点．（1）求k的值和点C的坐标；（2）求△OAC的周长．58．（2022•兰州）如图，点A在反比例函数y=kx（x＞0）的图象上，AB⊥x轴，垂足为B（3，0），过C（5，0）作CD⊥x轴，交过B点的一次函数y=32x+b的图象于D点，交反比例函数的图象于E点，S△AOB＝3．（1）求反比例函数y=kx（x＞0）和一次函数y=32x+b的表达式；（2）求DE的长．59．（2021•内江）如图，一次函数y＝k1x+b的图象与反比例函数y=k2x的图象相交于A（1，2）、B（﹣2，n）两点．（1）求一次函数和反比例函数的解析式；（2）根据图象，直接写出满足k1x+b＞k2x的x的取值范围；（3）若点P在线段AB上，且S△AOP：S△BOP＝1：4，求点P的坐标．60．（2021•湖北）如图，反比例函数y=kx的图象与一次函数y＝mx+n的图象相交于A（a，﹣1），B（﹣1，3）两点．（1）求反比例函数和一次函数的解析式；（2）设直线AB交y轴于点C，点N（t，0）是x轴正半轴上的一个动点，过点N作NM⊥x轴交反比例函数y=kx的图象于点M，连接CN，OM．若S四边形COMN＞3，求t的取值范围．。

中考数学总复习《反比例函数的性质》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．对于反比例函数y＝2x，下列说法正确是（）A．图象经过点（2，﹣1）B．图象位于第二、四象限C．图象是中心对称图形D．当x＜0时，y随x的增大而增大2．对于反比例函数y＝2x，下列说法不正确的是（）A．当x＜0时，y随x的增大而减小B．点（-2，-1）在它的图象上C．它的图象在第一、三象限D．当x＞0时，y随x的增大而增大3．如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数y=4x和y=2x的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为（）A．3B．4C．5D．64．已知反比例函数y=k x的图象如图所示，则一次函数y=kx+k的图象经过()A．第一、二、三象限B．第二、三、四象限C．第一、二、四象限D．第一、三、四象限5．若点M（﹣3，a），N（4，﹣6）在同一个反比例函数的图象上，则a的值为（）A．8B．﹣8C．﹣7D．56．函数y=1x+√x的图象在（）A．第一象限B．第一、三象限C．第二象限D．第二、四象限7．图所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的是A．当x=3时，EC＜EM B．当y=9时，EC＞EMC．当x增大时，EC·CF的值增大。

D．当y增大时，BE·DF的值不变。

8．已知函数y=−k 2+1x的图象经过点P1(x1，y1)，P2(x2，y2)，如果x2<0<x1，那么（）A．0<y2<y1B．y1>0>y2C．y2<y1<0D．y1<0<y29．已知双曲线y=k−1x向右平移2个单位后经过点（4，1），则k的值等于（）A．1B．2C．3D．510．对于反比例函数y=k x（k≠0），下列说法正确的是（）A．当k>0时，y随x增大而增大B．当k<0时，y随x增大而增大C．当k>0时，该函数图象在二、四象限D．若点（1，2）在该函数图象上，则点（2，1）也必在该函数图象上11．下列关于反比例函数y=8x的描述，正确的是（）A．它的图象经过点（12，4）B．图象的两支分别在第二、四象限C．当x＞2时，0＜y＜4D．x＞0时，y随x的增大而增大12．反比例函数y= 1x的图象的两个分支分别位于（）象限．A．一、二B．一、三C．二、四D．一、四二、填空题13．如图，已知点A、B在双曲线y= k x（x＞0）上，AC△x轴于点C，BD△y轴于点D，AC与BD 交于点P，P是AC的中点，若△ABP的面积为3，则k=.14．如图，矩形ABCD的顶点A和对称中心在反比例函数y＝k x（k≠0，x＞0）的图象上，若矩形ABCD的面积为16，则k的值为．15．已知反比例函数y= k x（k为常数，k≠0）的图象位于第一、第三象限，写出一个符合条件的k的值为．16．若反比例函数y=﹣mx的图象经过点（﹣3，﹣2），则当x＜0时，y随x的增大而．17．若点（4，m）与点（5，n）都在反比例函数y＝8x（x≠0）的图象上，则m n（填＞，＜或＝）.18．如图，A(1，1)，B(2，2)，双曲线y= k x与线段AB有公共点，则k的取值范围是。

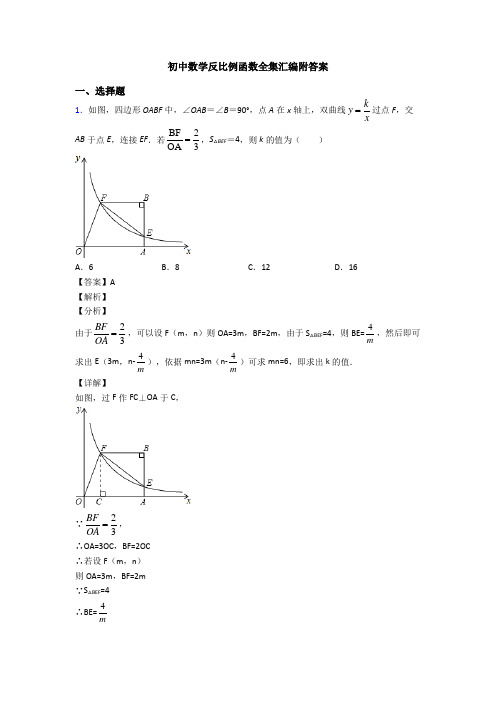
初中数学反比例函数全集汇编附答案一、选择题1．如图，四边形OABF中，∠OAB＝∠B＝90°，点A在x轴上，双曲线kyx=过点F，交AB于点E，连接EF．若BF2OA3=，S△BEF＝4，则k的值为（）A．6 B．8 C．12 D．16【答案】A【解析】【分析】由于23BFOA=，可以设F（m，n）则OA=3m，BF=2m，由于S△BEF=4，则BE=4m，然后即可求出E（3m，n-4m），依据mn=3m（n-4m）可求mn=6，即求出k的值．【详解】如图，过F作FC⊥OA于C，∵23 BFOA=，∴OA=3OC，BF=2OC ∴若设F（m，n）则OA=3m，BF=2m ∵S△BEF=4∴BE=4 m则E （3m ，n-4m ） ∵E 在双曲线y=k x 上 ∴mn=3m （n-4m） ∴mn=6即k=6．故选A ．【点睛】 此题主要考查了反比例函数的图象和性质、用坐标表示线段长和三角形面积，表示出E 点坐标是解题关键．2．如图，是反比例函数3y x =和7y x=-在x 轴上方的图象，x 轴的平行线AB 分别与这两个函数图象相交于点,A B ，点P 在x 轴上．则点P 从左到右的运动过程中，APB △的面积是（ ）A ．10B ．4C ．5D ．从小变大再变小【答案】C【解析】【分析】 连接AO 、BO ，由AB ∥x 轴，得ABP ABO S S =V V ，结合反比例函数比例系数的几何意义，即可求解．【详解】连接AO 、BO ，设AB 与y 轴交于点C ．∵AB ∥x 轴，∴ABP ABO S S =V V ，AB ⊥y 轴，∵73522ABO BOC AOC S S S -=+=+=V V V ，∴APB△的面积是：5．故选C．【点睛】本题主要考查反比例函数比例系数的几何意义，掌握反比例函数图象上的点与原点的连线，反比例函数图象上的点垂直于坐标轴的垂线段以及坐标轴所围成的三角形面积等于反比例函数比例系数绝对值的一半，是解题的关键．3．如图, 在同一坐标系中（水平方向是x轴），函数kyx=和3y kx=+的图象大致是（）A．B．C．D ．【答案】A【解析】【分析】根据一次函数及反比例函数的图象与系数的关系作答．【详解】解：A 、由函数y=k x 的图象可知k ＞0与y=kx+3的图象k ＞0一致，正确； B 、由函数y=k x 的图象可知k ＞0与y=kx+3的图象k ＞0，与3＞0矛盾，错误； C 、由函数y=k x 的图象可知k ＜0与y=kx+3的图象k ＜0矛盾，错误； D 、由函数y=k x的图象可知k ＞0与y=kx+3的图象k ＜0矛盾，错误． 故选A ．【点睛】本题主要考查了反比例函数的图象性质和一次函数的图象性质，要掌握它们的性质才能灵活解题．4．在平面直角坐标系中，分别过点(),0A m ,()2,0B m﹢作x 轴的垂线1l 和2l ,探究直线1l 和2l 与双曲线 3y x= 的关系，下列结论中错误．．的是 A ．两直线中总有一条与双曲线相交B ．当m =1时，两条直线与双曲线的交点到原点的距离相等C ．当20m -﹤﹤ 时，两条直线与双曲线的交点在y 轴两侧D ．当两直线与双曲线都有交点时，这两交点的最短距离是2【答案】D【解析】【分析】根据题意给定m 特定值、非特定值分别进行讨论即可得.【详解】当m =0时，2l 与双曲线有交点，当m =-2时，1l 与双曲线有交点，当m 0m 2≠≠，﹣时，12l l 与和双曲线都有交点，所以A 正确，不符合题意；当m 1=时，两交点分别是(1，3)，(3，1)，到原点的距离都是10，所以B 正确，不符合题意；当2m 0-﹤﹤ 时，1l 在y 轴的左侧，2l 在y 轴的右侧，所以C 正确，不符合题意；两交点分别是33m (m 2m m 2++，和，)，两交点的距离是()2364m m 2+⎡⎤+⎣⎦，当m 无限大时，两交点的距离趋近于2，所以D 不正确，符合题意，故选D.【点睛】本题考查了垂直于x 轴的直线与反比例函数图象之间的关系，利用特定值，分情况进行讨论是解本题的关键，本题有一定的难度.5．如图，点P 是反比例函数(0)k y k x=≠的图象上任意一点，过点P 作PM x ⊥轴，垂足为M . 连接OP . 若POM ∆的面积等于2. 5，则k 的值等于 （ ）A ．5-B ．5C ． 2.5-D ．2. 5【答案】A【解析】【分析】 利用反比例函数k 的几何意义得到12|k|=2，然后根据反比例函数的性质和绝对值的意义确定k 的值．【详解】解：∵△POM 的面积等于2.5，∴12|k|=2.5， 而k ＜0，∴k=-5，故选：A ．【点睛】本题考查了反比例函数系数k 的几何意义：在反比例函数y=k x图象中任取一点，过这一个点向x 轴和y 轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．也考查了反比例函数的性质．6．如图，反比例函数11k y x=的图象与正比例函数22y k x =的图象交于点（2，1），则使y 1＞y 2的x 的取值范围是（ ）A ．0＜x ＜2B ．x ＞2C ．x ＞2或-2＜x ＜0D ．x ＜－2或0＜x ＜2【答案】D【解析】【分析】 先根据反比例函数与正比例函数的性质求出B 点坐标，由函数图象即可得出结论.【详解】∵反比例函数与正比例函数的图象均关于原点对称，∴A 、B 两点关于原点对称.∵A （2，1），∴B （－2，－1）.∵由函数图象可知，当0＜x ＜2或x ＜－2时函数y 1的图象在y 2的上方，∴使y 1＞y 2的x 的取值范围是x ＜－2或0＜x ＜2.故选D.7．一次函数y=ax+b 与反比例函数a b y x-=，其中ab ＜0，a 、b 为常数，它们在同一坐标系中的图象可以是（ ） A ． B ．C ．D ．【答案】C【解析】【分析】根据一次函数的位置确定a 、b 的大小，看是否符合ab<0，计算a-b 确定符号，确定双曲线的位置．【详解】A. 由一次函数图象过一、三象限，得a>0，交y 轴负半轴，则b<0，满足ab<0，∴a −b>0，∴反比例函数y=a b x- 的图象过一、三象限， 所以此选项不正确； B. 由一次函数图象过二、四象限，得a<0，交y 轴正半轴，则b>0，满足ab<0，∴a −b<0，∴反比例函数y=a b x-的图象过二、四象限， 所以此选项不正确； C. 由一次函数图象过一、三象限，得a>0，交y 轴负半轴，则b<0，满足ab<0，∴a −b>0，∴反比例函数y=a b x-的图象过一、三象限， 所以此选项正确； D. 由一次函数图象过二、四象限，得a<0，交y 轴负半轴，则b<0，满足ab>0，与已知相矛盾所以此选项不正确；故选C.【点睛】此题考查反比例函数的图象，一次函数的图象，解题关键在于确定a 、b 的大小8．在平面直角坐标系xoy 中，函数()20y x x =<的图象与直线1l ：()103y x b b =+<交于点A ，与直线2l ：x b =交于点B ，直线1l 与2l 交于点C ，记函数()20y x x =<的图象在点A 、B 之间的部分与线段AC ，线段BC 围城的区域（不含边界）为W ，当4233b -≤≤-时，区域W 的整点个数为（ ） A ．3个 B ．2个 C ．1个D ．没有【答案】D【解析】【分析】根据解析式画出函数图象，根据图形W 得到整点个数进行选择.【详解】∵()20y x x=<，过整点（-1，-2），（-2，-1）， 当b=43-时，如图：区域W 内没有整点，当b=23-时，区域W 内没有整点，∴4233b -≤≤-时图形W 增大过程中，图形内没有整点， 故选：D.【点睛】 此题考查函数图象，根据函数解析式正确画出图象是解题的关键.9．如图，点P是反比例函数y=kx（x<0）图象上一点，过P向x轴作垂线，垂足为M，连接OP．若Rt△POM的面积为2，则k的值为（）A．4 B．2 C．-4 D．-2【答案】C【解析】【分析】根据反比例函数的比例系数k的几何意义得到S△POD=12|k|=2，然后去绝对值确定满足条件的k的值．【详解】解：根据题意得S△POD=12|k|，所以12|k||=2，而k＜0，所以k=-4．故选：C．【点睛】本题考查了反比例函数的比例系数k的几何意义：在反比例函数y=kx图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．10．函数kyx=与y kx k=-（0k≠）在同一平面直角坐标系中的大致图象是（）A ．B ．C ．D ．【答案】C【解析】【分析】分k>0和k<0两种情况确定正确的选项即可.【详解】当k:>0时，反比例函数的图象位于第一、三象限，一次函数的图象交 y 轴于负半轴，y 随着x 的增大而增大，A 选项错误，C 选项符合；当k<0时，反比例函数的图象位于第二、四象限，一次函数的图象交y 轴于正半轴，y 随着x 的增大而增减小，B. D 均错误，故选：C.【点睛】此题考查反比例函数的图象，一次函数的图象，熟记函数的性质是解题的关键.11．若点()11,A y -，()22,B y -，()33,C y 在反比例函数8y x =-的图象上，则y 1，y 2，y 3的大小关系是（ ）A ．123y y y <<B ．213y y y <<C ．132y y y <<D ．321y y y << 【答案】D【解析】【分析】由于反比例函数的系数是－8，故把点A 、B 、C 的坐标依次代入反比例函数的解析式，求出123,,y y y 的值即可进行比较.【详解】解：∵点()11,A y -、()22,B y -、()33,C y 在反比例函数8y x =-的图象上， ∴1881y =-=-，2842y =-=-，383y =-， 又∵8483-<<， ∴321y y y <<．故选：D ．【点睛】本题考查的是反比例函数的图象和性质，难度不大，理解点的坐标与函数图象的关系是解题的关键.12．如图，在平面直角坐标系中，将△OAB（顶点为网格线交点）绕原点O顺时针旋转90°，得到△OA′B′，若反比例函数y=kx的图象经过点A的对应点A′，则k的值为（）A．6 B．﹣3 C．3 D．6【答案】C【解析】【分析】直接利用旋转的性质得出A′点坐标，再利用反比例函数的性质得出答案．【详解】如图所示：∵将△OAB（顶点为网格线交点）绕原点O顺时针旋转90°，得到△OA′B′，反比例函数y=kx的图象经过点A的对应点A′，∴A′（3，1），则把A′代入y=kx，解得：k=3．故选C．【点睛】此题主要考查了反比例函数图象上点的坐标特征，正确得出A′点坐标是解题关键．13．如图,二次函数2y ax bx c =++的图象如图所示,则一次函数y ax c =+和反比例函数b y x=在同平面直角坐标系中的图象大致是（ ）A ．B ．C ．D ．【答案】D【解析】【分析】直接利用二次函数图象经过的象限得出a ，b ，c 的值取值范围，进而利用一次函数与反比例函数的性质得出答案．【详解】∵二次函数y=ax 2+bx+c 的图象开口向下，∴a ＜0，∵二次函数y=ax 2+bx+c 的图象经过原点，∴c=0，∵二次函数y=ax 2+bx+c 的图象对称轴在y 轴左侧，∴a ，b 同号，∴b ＜0，∴一次函数y=ax+c ，图象经过第二、四象限，反比例函数y=b x图象分布在第二、四象限， 故选D ．【点睛】此题主要考查了反比例函数、一次函数、二次函数的图象，正确把握相关性质是解题关键．14．反比例函数k y x=在第一象限的图象如图所示，则k 的值可能是（ ）A ．3B ．5C ．6D ．8【答案】B【解析】【分析】 根据点（1，3）在反比例函数图象下方，点（3，2）在反比例函数图象上方可得出k 的取值范围，即可得答案.【详解】∵点（1，3）在反比例函数图象下方，∴k>3，∵点（3，2）在反比例函数图象上方， ∴3k<2，即k<6， ∴3<k<6，故选：B.【点睛】 本题考查了反比例函数的图象的性质，熟记k=xy 是解题关键.15．如图，若点M 是x 轴正半轴上任意一点，过点M 作PQ ∥y 轴，分别交函数1(0)k y x x =>和2(0)k y x x=>的图象于点P 和Q ，连接OP 和OQ ．则下列结论正确的是（ ）A ．∠POQ 不可能等于90°B ．12PM QM k k =C ．这两个函数的图象一定关于x 轴对称D ．△POQ 的面积是()1212k k + 【答案】D【解析】【分析】【详解】解：根据反比例函数的性质逐一作出判断：A ．∵当PM=MO=MQ 时，∠POQ=90°，故此选项错误；B ．根据反比例函数的性质，由图形可得：1k ＞0，2k ＜0，而PM ，QM 为线段一定为正值，故12PM QM k k =，故此选项错误； C ．根据1k ，2k 的值不确定，得出这两个函数的图象不一定关于x 轴对称，故此选项错误；D ．∵|1k |=PM•MO ，|2k |=MQ•MO ，∴△POQ 的面积=12MO•PQ=12MO （PM+MQ ）=12MO•PM+12MO•MQ=()1212k k +． 故此选项正确．故选D ．16．在函数()0k y k x=<的图象上有()11,A y ，()21,B y -，()32,B y -三个点，则下列各式中正确的是（ ） A ．123y y y <<B ．132y y y <<C ．321y y y <<D ．231y y y <<【答案】B【解析】【分析】根据反比例函数图象上点的坐标特征得到11y k ⨯=，21y k -⨯=，32y k -⨯=，然后计算出1y 、2y 、3y 的值再比较大小即可．【详解】 解：(0)k y k x=<Q 的图象上有1(1,)A y 、2(1,)B y -、3(2,)C y -三个点， 11y k ∴⨯=，21y k -⨯=，32y k -⨯=， 1y k ∴=，2y k =-，312y k =-， 而k 0<，132y y y ∴<<．故选：B ．【点睛】 本题考查了反比例函数图象上点的坐标特征：反比例函数k y x=（k 为常数，且0k ≠）的图象是双曲线，图象上的点(),x y 的横纵坐标的积是定值k ，即xy k =．17．如图，矩形ABCD 的边AB 在x 轴上，反比例函数(0)k y k x =≠的图象过D 点和边BC 的中点E ，连接DE ，若△CDE 的面积是1，则k 的值是（ ）A ．3B ．4C ．25D ．6【答案】B【解析】【分析】 设E 的坐标是m n k mn =（，），， 则C 的坐标是2m n （，），求得D 的坐标，然后根据三角形的面积公式求得mn 的值，即k 的值．【详解】设E 的坐标是m n k mn =（，），，， 则C 的坐标是（m ，2n ），在mn y x = 中，令2y n =，解得：2m x =， ∵1CDE S =V ，∴111,12222m m n m n -=⨯=g 即 ∴4mn =∴4k =故选：B【点睛】本题考查了待定系数法求函数的解析式，利用mn 表示出三角形的面积是关键．18．如图，△AOB 是直角三角形，∠AOB ＝90°，△AOB 的两边分别与函数12,y y x x=-=的图象交于B 、A 两点，则等于（ ）A ．22B ．12C ．14D ．3 【答案】A【解析】【分析】过点A,B 作AC ⊥x 轴,BD ⊥x 轴,垂足分别为C,D.根据条件得到△ACO ∽△ODB.根据反比例函数比例系数k 的几何意义得出2()S OBD OB S AOC OA ∆=∆＝121＝12利用相似三角形面积比等于相似比的平方得出2OB OA = 【详解】 ∵∠AOB ＝90°，∴∠AOC +∠BOD ＝∠AOC +∠CAO ＝90°，∠CAO ＝∠BOD ，∴△ACO ∽△BDO ，∴2()S OBD OB S AOC OA∆=∆ , ∵S △AOC ＝12 ×2＝1，S △BOD ＝12×1＝12， ∴2()OB OA ＝121＝12 ， ∴2OB OA =， 故选A ．【点睛】此题考查了反比例函数图象上点的坐标特征和相似三角形的判定与性质，解题关键在于做辅助线，然后得到相似三角形再进行求解19．如图，A 、C 是函数1y x=的图象上任意两点，过点A 作y 轴的垂线，垂足为B ，过点C 作y 轴的垂线，垂足为D ．记Rt AOB ∆的面积为1S ，Rt COD ∆的面积为2S ，则1S 和2S 的大小关系是（ ）A ．12S S >B ．12S S <C ．12=S SD ．由A 、C 两点的位置确定【答案】C【解析】【分析】 根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=12k|． 【详解】由题意得：S 1=S 2=12|k|=12． 故选：C ．【点睛】本题主要考查了反比例函数y ＝k x中k 的几何意义，即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=12|k|，是经常考查的一个知识点；这里体现了数形结合的思想．20．如图，直线y 1＝x +b 与x 轴、y 轴分别交于A ，B 两点，与反比例函数y 2＝﹣5x （x ＜0）的图象交于C ，D 两点，点C 的横坐标为﹣1，过点C 作CE ⊥y 轴于点E ，过点D 作DF ⊥x 轴于点F ．下列说法正确的是（ ）A ．b ＝5B ．BC ＝ADC ．五边形CDFOE 的面积为35D ．当x ＜﹣2时，y 1＞y 2【答案】B【解析】【分析】根据函数值与相应自变量的关系，可得C 点坐标，根据待定系数法，可得一次函数解析式，可判断A 选项；根据解方程组，可得C 、D 点的坐标，根据全等三角形的判定与性质，可判断B 选项； 根据图形的分割，可得梯形、矩形，根据面积的和差，可判断C 选项；根据函数与不等式的关系：函数图象在上方的函数值大，可判断D 选项．【详解】解：由反比例函数y 2＝﹣5x （x ＜0）经过C ，点C 的横坐标为﹣1，得 y ＝﹣51-＝5，即C （﹣1，5）． 反比例函数与一次函数交于C 、D 点，5＝﹣1+b ，解得b ＝6，故A 错误；CE ⊥y 轴于E 点，E （0，﹣5），BE ＝6﹣5＝1．反比例函数与一次函数交于C 、D 点，联立65y x y x =+⎧⎪⎨=-⎪⎩， x 2+6x +5＝0解得x 1＝﹣5，x 2＝﹣1，当x ＝﹣5时，y ＝﹣5+6＝1，即D （﹣5，1），即DF ＝1，在△ADF 和△CBE 中，DAF BCE AFD CEB DF BE ∠=∠⎧⎪∠=∠⎨⎪=⎩，△ADF ≌△CBE （AAS ），AD＝BC，故B正确；作CG⊥x轴，S△CDFOE＝S梯形DFGC+S矩形CGOE＝()(15)422DF CG FGOG CG++⨯+g+1×5＝17，故C错误；由一次函数图象在反比例函数图象上方的部分，得﹣5＜x＜﹣1，即当﹣5＜x＜﹣1时，y1＞y2，故D错误；故选：B．【点睛】本题考查了反比例函数综合题，利用了自变量与函数值的对应关系，点的坐标与函数解析式的关系，全等三角形的判定与性质，图形分割法求图形的面积，函数图象与不等式的关系．。

北师大版数学九年级上册第六章反比例函数6・2反比例函数的图象与性质反比例函数的性质专题训练题1•下列说法中不正确的是（）A・函数y = 2x的图象经过原点B・函数的图象位于第一、三象限X3C・函数y = 3x—l的图象不经过第二彖限D・函数y=—三的值随X的值的增大而增大3 .・一2•反比例函数y=—：的图象上有P|（X] »—2），P2（X2 '一3）两点‘则X]与X2的大小关系是（）A.A ・ X|>X2 B・ X1=X2 C • X|<X2D・不确定33•若点A（-5，yi），B（—3 »），C（2，y?）在反比例函数y=;的图象上，则yi y y的大小关系是（）A ・ yi<y3<y2 B. yi<y2<y3 C ・ y3<y2<yi D. y2<yi<y34•已知函数y=乎的图象如图所示，则以下结论：®m<0；②在每个分支上y随x的增大而增大；③若点A（-l，a），点B（2，b）在图象上，则a <b；④若点P（x，y）在图象上，则点Pi（-x，y）也在图象上.其中正确的个数为（）A - 4 B. 3 C・ 2 D・ 12 —k5在反比例函数y= 丁的图象的每一条曲线上y都随着x的增大而减小则k的取值范围是_______________ 6•如图，直线y=kix+b与双曲线y=¥相交于点A d ' 2），B（m，— 1）两点.A（1）分别求直线和双曲线的表达式；⑵若Ai（xi，yj，A2（X2，y2），A3（x3，y3）为双曲线上的三点，且X]<x2<O<x3，请直接写出y「y2，y3的大小关系.47•如图，点P在反比例函数y=—；的图象上，PB丄y轴于点B，点A在x轴上^'JAPAB的而积是（）x48•如图，在平面直角坐标系中，过点M（-3，2）分别作x轴、y轴的垂线与反比例函数y=;的图象交于A，B两点，则四边形MAOB的面积为 ____________ ・9•如图，点A在双曲线y=;上，AB丄x轴于点B，且AAOB的面积为4，则双曲线的表达式为______—a — J10•在函数y= - （a为常数）的图象上有三点（一3，yi厂L1 '月A（2 y3）则函数值y「y2，y3x的大小关系为____________ .k11•已知A（x「yi），B（X2‘ y2）是反比例函数y=；（kH0）图象上的两个点‘当xi<x2<0时‘ yi>y2 '那X么一次函数y=kx—k的图象不经过（）A・第一象限B.第二象限C・第三象限D.第四象限?12•已知A（x「yi） ' B（X2 tA C（X3，y3）是反比例函数y=；上的三点‘若xi<x2<x3‘ y2<yi<y3 '则X下列关系式不正确的是（）A • X| • X2<0 B・X| • X3<0 C ・X2 • X3<0D・ X|+x2<013•如图，直线1丄X轴于点P，II与反比例函数yi=¥（x>0）及y2=¥（x>0）的图彖分别交于点A ‘ B，A A连接OA，OB，已知AOAB的面积为2，则k]-k2= __________ .V14•已知反比例函数yi=~的图象与一次函数y2=ax + b的图象交于点A（1，4）和点B（m ‘ ~2）.(1) 求这两个函数的表达式；(2) 观察图象，当x>0时，直接写出力>力时自变量x 的取值范围;(3) 如果点C 与点A 关于x 轴对称‘求AABC 的面积.15 •如图，在平面直角坐标系中，点P(1 ‘ 4)，Q(m ，n)在函数y =g(x>0)的图象上，当m>l 吋，过点 X P 分别作X 轴、y 轴的垂线‘垂足为点A ，B ；过点Q 分别作x 轴、y 轴的垂线，垂足为点C ，D.QD 交PA 于点E ‘随着m 的增大‘四边形ACQE 的面积(16・如图，在平面直角坐标系屮，正方形OABC 的顶点O 与坐标原点重合，点C 的坐标为(0，3)，点A 在x 轴的负半轴上，点D ，M 分别在边AB ，OA 上，且AD=2DB ，AM=2MO ，—次函数y=kx+b 的 图象过点D 和M ，反比例函数丫=弓的图象经过点D ，与BC 的交点为N. A(1) 求反比例函数和一次函数的表达式；(2) 若点P 在直线DM 上，且使AOPM 的面积与四边形OMNC 的面枳相等，求点P 的坐标.C ・先减小后增大 D. 先增大后减小A A/\ O v答案：1—4 DADC5.k<21 c6.（l）Vy=-^ii点A（1，2），・・.k2=2，・・.y=;，当y= —1 时，m=—2 ? /.y=k|x + b 过点A（1，2），X XB（—2，—1），.•.ki = l，b= 1 ? Ay = x4-1. （2） y2<yi<y3.7. B& 1010・ Y3<yi<Y211. B12. A13. 4k 414.（1）・・・点A（1，4）在上，・・・k=4，yi=;，・••点B在力上，.-.m=-2.A点B（-2 ‘一2），T点A，X X• 4B 在y2=ax+b 上，「•求得a=2、b=2，•；y2=2x+2，•:这两个函数的表达式为yi=—，y2=2x+2.x（2）由图象可知，当0<x<l时，yi>y2・⑶・・•点C与点A关于x轴对称，・・・C（1，一4），过B点作BD丄AC于点D，图略，则D（1，—2），.・.△ ABC 的咼为BD= 1 —（—2） = 3，底AC=8，S AABC =12.15. B16.（I）：正方形OABC 的顶点C（0，3），AOA = AB = BC = OC = 3，ZOAB= ZB= ZBCO = 90°，T AD = 2DB，・・.AD=£A B=2 » AD（—3，2）.把D点坐标代入y=^，得m=—6，・••反比例函数的表达式为y=—£，TAM = 2MO，.•.MO=*OA=1，即Me—1 » 0），把点M 与点D 的坐标代入y=kx+b 中»-k+b=0、_3k + b=2，k=_l， 6解得1 1则一次函数的表达式为y=—x—l.⑵把y = 3代入y=—：'得x = —2，b= —l，x・・・N（— 2，3），即NC = 2，设P（x，y），•••△OPM的而积与四边形OMNC的而积相等，.\|oM|y|=|（OM +NC） OC，即|y|=9，解得y=±9，当y=9 时，x= —10，当y=—9 时，x=8，则点P 的坐标为（一10，9）或（8 ‘一9）・。

2011-2023北京中考真题数学汇编反比例函数7．（2014北京中考真题）如图，在平面直角坐标系(0)ky k x=≠，使它的图象与正方形9．（2011北京中考真题）如图，在平面直角坐标系图象的一个交点为A（﹣（1）求反比例函数y=（2）若P是坐标轴上一点，且满足10．（2018北京中考真题）在平面直角坐标系线14l y x b=+∶与图象G（1）求k的值；∴由上述结果可知，分母不能为，故【点睛】本题考查反比例函数与一次函数的交点问题，曲线上点的坐标与方程的关系．9．（1）y=﹣2x；（2）（【详解】解：（1）∵点∴n=﹣2×（﹣1）=2∴点A的坐标为（﹣1∵点A在反比例函数的图象上．∴k=﹣210．（1）4；（2）①3个．【详解】分析：（1）根据点（2）①当1b =-时，根据整点的概念，直接写出区域②分a ．当直线过（4，0时四种情况进行讨论即可详解：（1）解：∵点A （∴14k=，∴4k =．（2）①3个．（1，0），（②a ．当直线过（4，0）时：b ．当直线过（5，0）时：c ．当直线过（1，2）时：1124b ⨯+=，解得74b =d ．当直线过（1，3）时：1134b ⨯+=，解得114b =∴综上所述：514b -≤<-或71144b <≤．点睛：属于反比例函数和一次函数的综合题，考查待定系数法求反比例函数解析式，一次函数的图象与性质，掌握整点的概念是解题的关键,注意分类讨论思想在解题中的应用.11．（1）1(0)y x x =>不是有界函数，y=x+1(-4<x ≤2)是有界函数，边界值是3；（2）-1＜b≤3；（3）0≤m≤14或34≤m≤1．【分析】（1）分析题意，结合已知中有界函数的定义可进行判断；（2）根据一次函数的性质可得1y x =-+的增加性，再结合自变量的取值范围和题意可得此不等式组可得b 的取值范围；（3）要分情况讨论，易判断1m >不符合题意，故1m；结合已知函数解析式可得函数过点以此求得其平移后的点坐标，进而可得34≤1-m≤1或-1≤-m≤34，由此即可求得m 【详解】解：（1）结合已知根据有界函数的定义可知1(0)y x x=>不是有界函数，数，边界值是3；（2）1y x =-+Q 中10-<，y 随x 的增大而减小，∴当x a =时，12=-+=y a ，故1a =-．当x b =时，1=-+y b ，根据题意可得：212b b a--+<⎧⎨>⎩ ，31b ∴>- ；（3）若1m >，函数向下平移m 个单位后，0x =时，函数值小于1-，此时函数的边界值不符，故1m．当=1x -时，1y =，即过(1,1)-，当0x =时，0min y =，即过(0,0)，将(1,1)-，(0,0)都向下平移m 个单位，得到(1,1)m --，(0,)m -，根据题意可得：1m t -=或m t -=，∴34≤1-m≤1或-1≤-m≤34，0≤m≤14或34≤m≤1．【点睛】本题考查了二次函数综合题，解题的关键是结合新定义，弄清函数边界值的定义，同时要熟悉平移变换的性质．。

反比例函数》测试题(含答案)1、选择题（每小题5分，共50分）1、若点（x1.-1）、(x2.-2)、(x3.1)都在反比例函数y= k/x 上，则它们之间的大小关系是（）A．x1<x3<x2B．x2<x1<x3C．x1<x2<x3D．x2<x3<x12、若反比例函数y=k/x的图象经过点(m，3m)，其中m≠0，则此反比例函数的图象在（）A．第一、二象限；B．第一、三象限；C．第二、四象限；D．第三、四象限3、在直角坐标系中，点A是x轴正半轴上的一个定点，点B是双曲线y=3/x上的一个动点，当点B的横坐标逐渐增大时，△OAB的面积将会（）A．逐渐增大B．不变C．逐渐减小D．先增大后减小4、函数y=-kx与函数y=k/x的图象的交点个数是（）A。

0B。

1C。

2D.不确定5、函数y=6-x与函数y=k/x的图象交于A、B两点，设点A的坐标为（x1,y1），则边长分别为x1、y1的矩形面积和周长分别为（）A。

4，12B。

4，6C。

8，12D。

8，66、已知y1+y2=y，其中y1与x成反比例,且比例系数为k1，而y2与x2成正比例,且比例系数为k2，若x=-1时,y=0，则k1,k2的关系是( )A.k1+k2=0B.k1k2=1C.k1-k2=0D.k1k2=-17、正比例函数y=2kx与反比例函数y=k/(x-1)在同一坐标系中的图象不可能是（）18、如图，直线y=mx与双曲线y=k/(x-1)交与A、B两点，过点A作AM⊥x轴，垂足为M，连接BM，若S△ABM=2，则k的值是（）A、2B、m-2C、mD、49、如图，点A在双曲线y=6/x上，且OA＝4，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为( )A.47B.5C.27D.2210、如图，反比例函数y= k/x的图象经过点(1,2)，则k=（）。

二、填空题（每小题5分，共20分）11、若y=k/x是反比例函数，且x1y1=x2y2，则k=______。

反比例函数练习题集锦（含答案）1、综合题1、如图，已知直线与双曲线交于两点，且点的横坐标为．（1）求的值；（2）若双曲线上一点的纵坐标为8，求的面积；（3）过原点的另一条直线交双曲线于两点（点在第一象限），若由点为顶点组成的四边形面积为，求点的坐标．2、已知一次函数与双曲线在第一象限交于A、Ｂ两点，A点横坐标为1．B点横坐标为４(1)求一次函数的解析式;(2)根据图象指出不等式的解集；(2) 点P是x轴正半轴上一个动点，过P点作x轴的垂线分别交直线和双曲线于M、N，设P点的横坐标是t(t>0),△OMN的面积为S,求S和t的函数关系式，并指出t的取值范围。

二、简答题3、．已知：如图，在平面直角坐标系中，直线AB 分别与轴交于点B、A，与反比例函数的图象分别交（1）求该反比例函数的解析式；（2）求直线AB的解析式．4、如图，已知正比例函数与反比例函数的图象交于两点．（1）求出两点的坐标；的范围；（2）根据图象求使正比例函数值大于反比例函数值的三、计算题5、为了预防流感，某学校在休息天用药熏消毒法对教室进行消毒。

已知药物释放过程中，室内每立方米空气中含药量y（毫克）与时间t（小时）成正比；药物释放完毕后，y与t 的函数关系为（为常数）。

如下图所示，据图中提供的信息，解答下列问题：（1）写出从药物释放开始，y与t之间的两个函数关系式及相应的自变量取值范围；（2）据测定，当空气中每立方米和含药量降低到0.25毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室？6、如图，在直角坐标系xOy中，一次函数y＝k1x＋b 的图象与反比例函数的图象交于A(1，4).B(3，m)两点。

(1)求一次函数的解析式；的面积。

(2)求△AOB7、如图,一次函数y=kx+b的图象与反比例函数y=图象交于A(－2,1)、B(1,n)两点.(1) 求反比例函数和一次函数的解析式.(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.（1）试确定上述反比例函数和一次函数的表达式；（2）求△AOB的面积。