棱柱棱锥
- 格式:ppt
- 大小:1.16 MB
- 文档页数:29



棱柱和棱锥知识点归纳总结### 棱柱知识点归纳总结一、定义与分类- 棱柱:由两个平行的多边形面和若干个平行四边形侧面组成的几何体。
- 分类:- 按多边形面的形状:三棱柱、四棱柱(长方体)、五棱柱、六棱柱等。
- 按侧面的形状:直棱柱(侧面与底面垂直)、斜棱柱(侧面与底面不垂直)。
二、几何特性- 所有侧棱相互平行。
- 相邻两个侧面的交线是一条直线,称为棱。
- 两个平行多边形面称为底面,其余的面称为侧面。
三、体积计算- 体积公式:V = 底面积× 高。
- 其中,高指的是两个平行多边形面之间的距离。
四、表面积计算- 表面积公式:S = 2 × 底面积 + 侧面积。
- 侧面积 = 底面周长× 高。
五、特殊棱柱- 正棱柱:所有侧面都是全等的矩形。
- 长方体:底面为矩形的四棱柱。
- 正方体:底面为正方形的长方体。
六、易错点- 容易混淆棱柱的高与侧面的边长。
- 计算体积时忘记乘以高。
- 计算表面积时漏掉底面积或侧面积。
经典例题及解题步骤1. 例题:求一个底面为正方形,边长为2,高为3的正方体的体积。
- 解题步骤:1. 确定底面为正方形,边长a=2。
2. 确定高h=3。
3. 应用体积公式:V = a^2 × h。
4. 计算:V = 2^2 × 3 = 12。
2. 例题:求一个底面为等边三角形,高为4的正三棱柱的表面积。
- 解题步骤:1. 确定底面为等边三角形,边长a。
2. 应用等边三角形面积公式:A = (sqrt(3)/4) × a^2。
3. 确定高h=4。
4. 计算侧面积:S_side = 3 × (sqrt(3)/2) × a × h。
5. 应用表面积公式:S = 2 × A + S_side。
6. 计算:S = 2 × (sqrt(3)/4) × a^2 + 3 × (sqrt(3)/2) × a × 4。
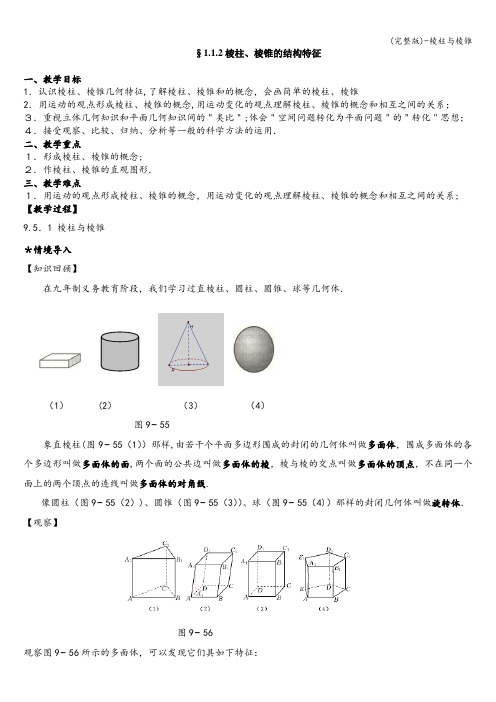
§1.1.2棱柱、棱锥的结构特征一、教学目标1.认识棱柱、棱锥几何特征,了解棱柱、棱锥和的概念,会画简单的棱柱、棱锥2.用运动的观点形成棱柱、棱锥的概念,用运动变化的观点理解棱柱、棱锥的概念和相互之间的关系;3.重视立体几何知识和平面几何知识间的"类比";体会"空间问题转化为平面问题"的"转化"思想;4.接受观察、比较、归纳、分析等一般的科学方法的运用.二、教学重点1.形成棱柱、棱锥的概念;2.作棱柱、棱锥的直观图形.三、教学难点1.用运动的观点形成棱柱、棱锥的概念,用运动变化的观点理解棱柱、棱锥的概念和相互之间的关系;【教学过程】9.5.1 棱柱与棱锥*情境导入【知识回顾】在九年制义务教育阶段,我们学习过直棱柱、圆柱、圆锥、球等几何体.(1) (2)(3)(4)图9−55象直棱柱(图9−55(1))那样,由若干个平面多边形围成的封闭的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱与棱的交点叫做多面体的顶点,不在同一个面上的两个顶点的连线叫做多面体的对角线.像圆柱(图9−55(2))、圆锥(图9−55(3))、球(图9−55(4))那样的封闭几何体叫做旋转体.【观察】图9−56观察图9−56所示的多面体,可以发现它们具如下特征:(1)有两个面互相平行,其余各面都是四边形;(2)每相邻两个四边形的公共边互相平行.*引入新知有两个面互相平行,其余每相邻两个面的交线都互相平行的多面体叫做棱柱,互相平行的两个面,叫做棱柱的底面,其余各面叫做棱柱的侧面.相邻两个侧面的公共边叫做棱柱的侧棱.两个底面间的距离,叫做棱柱的高.根据棱柱的底面可以是三角形、四边形、五边形等这样的棱柱叫做三棱柱、四棱柱、五棱柱等图9−56所示的四个多面体都是棱柱.表示棱柱时,通常分别顺次写出两个底面各个顶点的字母,中间用一条短横线隔开,例如,图9−56(2)所示的棱柱,可以记作棱柱1111ABCD A B C D -,或简记作棱柱1AC .经常以棱柱底面多边形的边数来命名棱柱,如图9−56所示的棱柱依次为三棱柱、四棱柱、五棱柱. 侧棱与底面斜交的棱柱叫做斜棱柱,如图9−56(2);侧棱与底面垂直的棱柱叫做直棱柱,如图9−56(1);底面是正多边形的直棱柱叫做正棱柱,如图9−56(3)和(4),分别为正四棱柱和正五棱柱.正棱柱有下列性质:(1)侧棱垂直于底面,各侧棱长都相等,并且等于正棱柱的高;(2)两个底面中心的连线是正棱柱的高.例1。

