棱柱、棱锥和棱台的结构特征资料讲解
- 格式:doc
- 大小:111.50 KB
- 文档页数:10

棱柱棱台棱锥知识点总结一、棱柱的定义和性质1. 棱柱的定义:棱柱是一个多边形和一个平行于它的平面所围成的几何图形。
2. 棱柱的特征:(1)棱柱的底面是一个多边形,顶面与底面平行,并且顶面的每个点和底面的对应点之间的连线都垂直于底面。
(2)如果底面是正多边形,棱柱就称为正棱柱;如果底面是不规则多边形,棱柱就称为斜棱柱。
(3)棱柱的高等于顶面到底面的距离,底面的面积乘以高就是棱柱的体积。
二、棱台的定义和性质1. 棱台的定义:棱台是由平行多边形和连通它们的矩形棱所围成的空间图形。
2. 棱台的特征:(1)如果底面和顶面都是正多边形,且它们的对边平行,那么这个棱台称为正棱台;如果底面和顶面是正多边形,但它们不一定平行,那么这个棱台称为斜棱台。
(2)棱台的体积等于底面积与高的乘积,而斜棱台的体积还需要乘以一个高与底面中较大边的比值。
三、棱锥的定义和性质1. 棱锥的定义:棱锥是由一个多边形和以它为底的三棱锥棱所围成的几何图形。
2. 棱锥的特征:(1)如果底面是正多边形,棱锥称为正棱锥;如果底面不是正多边形,那么棱锥就称为斜棱锥。
(2)棱锥的体积等于底面积与高的乘积,并除以3。
(3)棱锥的侧棱的延长线与底面平面的交点称为顶点。
四、棱柱、棱台、棱锥的计算公式1. 棱柱的体积公式:V=Sh,其中V表示棱柱的体积,S表示底面的面积,h表示高。
2. 棱台的体积公式:V=(S1+S2+√S1S2)h/3,其中V表示棱台的体积,S1和S2表示底面和顶面的面积,h表示高。
3. 棱锥的体积公式:V=Sh/3,其中V表示棱锥的体积,S表示底面的面积,h表示高。
以上就是关于棱柱、棱台、棱锥的知识点总结,希望对你有所帮助。
如果还有其他问题,欢迎继续提问。









理解立体几何中的棱柱棱锥和棱台的特点在立体几何学中,棱柱、棱锥和棱台是常见的几何体。
它们都是由多个多边形组成,具有不同的特点和性质。
本文将详细介绍棱柱、棱锥和棱台的特点,以及它们在日常生活中的应用。
一、棱柱的特点1.1 定义棱柱是由两个平行且相等多边形底面和连接底面的矩形侧面构成的几何体。
棱柱的底面可以是任意多边形,而矩形侧面的长度等于底面的周长。
1.2 特点(1)棱柱有两个底面,它们是平行且相等的多边形。
(2)棱柱的侧面是矩形,长宽分别等于底面周长和底面之间的距离。
(3)棱柱的顶点连接两个底面的对应顶点,顶点与底面的连接线段被称为棱柱的高。
(4)面的个数:侧 + 2个底面,其中侧面个数等于底面的边数。
(5)棱柱的体积可以通过底面积乘以高来计算,公式为V = 底面积 ×高。
1.3 应用棱柱在日常生活中有很多应用,例如:(1)建筑工程中的柱子、电线杆等都是棱柱的形状。
(2)常见的马克杯、鼓棒等也是棱柱的形状。
二、棱锥的特点2.1 定义棱锥是由一个多边形底面和连接底面的三角形侧面构成的几何体。
棱锥的底面可以是任意多边形,而三角形侧面的高等于棱锥的高,并与底面相交于一个顶点。
2.2 特点(1)棱锥有一个底面,其他面都是三角形。
(2)棱锥的底面可以是任意多边形,而三角形侧面的高等于棱锥的高。
(3)棱锥的顶点连接底面的每个顶点,顶点与底面的连接线段被称为棱锥的高。
(4)面的个数:侧 + 1个底面,其中侧面个数等于底面的边数。
(5)棱锥的体积可以通过底面积乘以高再除以3来计算,公式为V = 底面积 ×高 / 3。
2.3 应用棱锥在日常生活中也有很多应用,例如:(1)常见的路灯、红绿灯、教师讲台等都是棱锥的形状。
(2)糖果塔、圆锥形帽子等也是棱锥的形状。
三、棱台的特点3.1 定义棱台是由两个平行且相等多边形底面和连接底面的梯形侧面构成的几何体。
棱台的底面可以是任意多边形,而底面和梯形侧面的高度相等。
棱柱、棱锥和棱台的
结构特征
教案
主编:林鹤审核人:备课人:林鹤备课时间:使用时间:
(2)棱柱的这两个互相平行的面叫做棱柱的底面,其余各面叫做棱柱的侧面,两侧面的公共边叫做棱柱的侧棱,两底面之间的距离叫做棱柱的高.
(3)棱柱按底面是三角形、四边形、五边形……分别叫做三棱柱、四棱柱、五棱柱……
(4)侧棱与底面不垂直的棱柱叫做斜棱柱,侧棱与底面垂直的棱柱叫做直棱柱,底面是正多边形的直棱柱叫做正棱柱.
(5)底面是平行四边形的棱柱叫做平行六面体,侧棱与底面垂直的平行六面体叫做直平行六面体,底面是矩形的直平行六面体是长方体,棱长都相等的长方体是正方体.
例1下列命题中正确的是()
A.棱柱的面中,至少有两个面互相平行
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.在平行六面体中,任意两个相对的面均互相平行,但平行六面体的任意两个相对的面不一定可当作它的底面
D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形
7.正三棱柱ABC—A′B′C′的底面边长是4 cm,过BC的一个平面交侧棱AA′于D,若AD的长是2 cm,试求截面BCD的面积.
解如图,取BC的中点E,
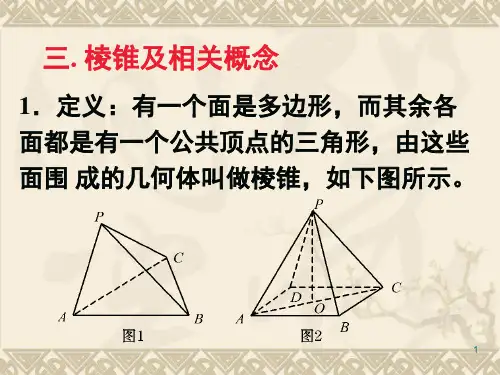
探究点三棱锥的结构特征
思考1我们把下面的多面体取名为棱锥,据此你能给棱锥下一个定义吗?棱锥的底面、侧面、侧棱、顶点分别是什么含义?你能作图加以说明吗?
解设VO为正四棱锥V—ABCD的高,作OM⊥BC于点M,则M 为BC中点.
13.已知正四棱锥S-ABCD的高为3,侧棱长为7.
(1)求侧面上的斜高;
(2)求一个侧面的面积;
(3)求底面的面积.
.
4.棱台
(1)棱锥被平行于底面的平面所截,截面和底面间的部分叫做棱台.原棱锥的底面和截面分别叫做棱台的下底面、上底面;其他各面叫做棱台的侧面;相邻两侧面的公共边叫做棱台的侧棱;两底面间的距离叫做棱台的高.
(2)由正棱锥截得的棱台叫做正棱台.
(3)正棱台各侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高.
例:已知正四棱台的上、下底面面积分别为4、16,一侧面面积为12,分别求该棱台的斜高、高、侧棱长.
解如图,设O′,O分别为上、下底面的中心,即OO′为正四棱台的高,E,F分别为B′C′,BC的中点,。