摩尔电导率

§7.2 电解质溶液的电导率和摩尔电导率1. 电导和电导率通过溶液的电流强度I 与溶液电阻R 和外加电压V 服从欧姆定律R ＝V/I ；而溶液的电阻率ρ可根据(/)R A l ρ=计算。

通过测量电阻（resistance, R ）和电阻率（resistivity, ρ）即可评价电解质溶液的导电能力，不同的是l 为两电极间的距离，而A 则取浸入溶液的电极面积。

习惯上多用电导（conductance ，G ）和电导率（conductivity, κ）来表示溶液的导电能力，定义：G ＝1/R κ=1/ρ电导G 的单位是Ω-1，也记为S(西门子)，κ的单位是S·m -1。

电导和电导率间的关系：l G A κ⎛⎫=⎪⎝⎭(7.3)2. 电导的测量通常采用电导率仪（conductometer ）来测量电解质溶液的电导，其原理如图7.2。

测量时将电导电极（conductance electrode ）插入待测溶液或将待测溶液充入具有两个固定Pt 电极的电导池（conductance cell ）M 中，而后将M 连入惠斯登(Wheatstone)电桥的一臂。

测量方法与测定金属的电阻相同但技术上需做一些改进，如测量时不用直流电源而改用1000 Hz 的高频交流电源S ；以耳机或示波器T 来指示桥中零电流；在电桥另一臂的可变电阻R 1上需串联一个可变电容器K 以补偿电导池的电容。

电桥平衡时有314R R R R = 3141R G R R R ==（7.4） 溶液的电导率可按(7.3)式求算。

式中(l ／A)称为电导池常数（conductance cell constant ）。

不同的电导池具有不同的电导池常数，即使是同一电导池，其电导池常数也会随时间而改变。

实际测量时多用标准溶液（standard solution ）法，即先将一精确已知电导率（κs ）的标准溶液充入电导池，在指定温度下测定其电导（G s ），而后再将待测溶液充入该电导池测量其电导（G ），分别带入(7.3)式比较可得：ssGG κκ= (7.5) 式中不再出现电导池常数。

无限稀释摩尔电导率和电导率的关系下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!关于无限稀释摩尔电导率和电导率的关系,可以从以下几个方面进行阐述:1. 无限稀释摩尔电导率的定义。

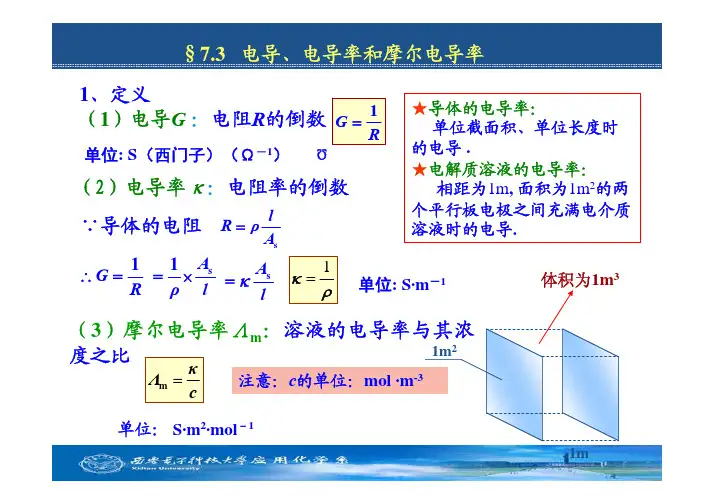
§7.3 电导、电导率和摩尔电导率1、定义（1）电导G ：电阻R 的倒数（2）电导率κ：电阻率的倒数（3）摩尔电导率Λm ：溶液的电导率与其浓度之比单位：S·m 2·mol －1单位: S （西门子）（Ω－1）Ω★导体的电导率：单位截面积、单位长度时的电导.★电解质溶液的电导率：相距为1m , 面积为1m 2的两个平行板电极之间充满电介质溶液时的电导.1m 21m c κΛ=m s l R ρA =ρκ1=单位: S·m －1∵导体的电阻1G R =1G R ∴=s A l κ=s 1A ρl =×体积为1m 3注意：c 的单位：mol ·m -3（1）电导的测定—惠斯通电桥采用适当频率的交流电源接通电源，移动接触点C ，使CD 间的电流为零。

此时，电桥平衡：431=R R R R x 溶液的电导溶液的电导率电导池系数（2）电导率、摩尔电导率的计算◆测定已知电导率为κ的溶液电阻（电导），求电导池系数K cell 。

◆同法测待测溶液电阻（电导），可计算电导率◆当待测溶液浓度c 已知时，可计算摩尔电导率待测电阻可变电容（抵消电导池电容）交流电源检零器电阻箱电阻R 3、R 4为AC 与CB 的电阻cκΛ=m 2、电导的测定4例：25℃时在一电导池中盛以c 为0.02 mol ⋅dm −3的KCl 溶液，测得其电阻为82.4 Ω。

若在同一电导池中盛以c 为0.025 mol ⋅dm −3的K 2SO 4溶液,测得其电阻为326.0 Ω。

已知25℃时0.02 mol ⋅dm −3的KCl 溶液的电导率为0.2768 S ⋅m -1。

试求：(1)电导池系数K cell ；(2) 0.0025 mol ⋅dm −3K 2SO 4溶液的电导率和摩尔电导率。

解：（1）电导池系数K cell =l /A s =κ(KCl).R (KCl)=(0.2768×82.4)m -1=22.81m -1（2）0.0025 mol/dm 3的K 2SO 4 溶液的电导率κ(K 2SO 4)= K cell /R (K 2SO 4)=(22.81/326.0) S ·m -1=0.06997S ·m -10.0025 mol/dm 3的K 2SO 4的溶液的摩尔电导率Λm (K 2SO 4) = κ(K 2SO 4)/c = (0.06997/2.5) S·m 2 ·mol -1= 0 .02799 S·m 2 ·mol -13．摩尔电导率与浓度的关系＃强电解质①溶液浓度↓，摩尔电导率↑②溶液浓度→零，曲线→直线，摩尔电导率趋于极限值，称无限稀释时的摩尔电导率，也称极限摩尔电导率由图可知：无论是强或弱电解质，摩尔电导率均随溶液的稀释而增大。

35℃时醋酸的极限摩尔电导率
我们要找出35℃时醋酸的极限摩尔电导率。

首先，我们需要了解什么是极限摩尔电导率。

极限摩尔电导率（Λ∞）是指在无限稀释的溶液中，每摩尔离子所具有的电导率。

它与溶液的离子浓度和离子迁移率有关。

对于一个特定的电解质，极限摩尔电导率是一个常数，它不依赖于溶液的浓度。

数学公式表示为：
Λ∞= k ×(1 + 0.5×z^2/RT)
其中，k是离子迁移率，z是离子的化合价，R是气体常数，T 是绝对温度。

对于醋酸（HAc），它是一个弱电解质，在35℃时的离子化合价z=1，k值约为0.02S·m^2/mol。

我们可以使用上述公式来计算极限摩尔电导率。

计算结果为：35℃时醋酸的极限摩尔电导率为0.020004 S·m^2/mol。

摩尔电导率表摩尔电导率表名称：摩尔电导率表。

摩尔电导率表是以各元素的电子在物质中所占的相对百分数而得到的比例。

摩尔电导率表可以将两种不同物质的分界线或混合物中各组成成分的相对含量变化状况一目了然地显示出来。

本实验主要用于测定溶液的电导率，制作电导率表等方面的应用。

下面请大家跟随我做这个实验吧！它可以把两种不同物质的分界线或混合物中各组成成分的相对含量变化状况一目了然地显示出来。

通过读取电导率值，就可以计算出被测液体中某种离子的百分含量。

用的工具很简单，那就是一支试剂瓶、一张玻璃板和一些蒸馏水。

首先我们需要准备好所需材料：试剂瓶一个、橡胶管两根、烧杯若干、玻璃板一块、蒸馏水少许。

好，准备好之后我们开始进行实验吧！首先，在一张玻璃板上用铅笔画好直角三角形，以此作为摩尔电导率表的底座，也可以称其为定标点，然后将另一张玻璃板倒扣在底座上，用小刀切掉多余部分。

第二步，用酒精棉球擦拭底座，以使其保持清洁。

接着，我们用清水清洗底座及玻璃板，再用自来水冲洗干净。

第三步，在一个新的烧杯里放入适量的蒸馏水，并注入足够量的蒸馏水，放置在底座的中心位置。

然后，在另一个新的烧杯里装入1/10体积的自来水，并注入适量的蒸馏水。

这样，当然是为了确保每个摩尔电导率表的电导率范围都是一样的。

第四步，在第三个烧杯里放入准备好的待测液，液面与底座上的切点齐平。

注意，因为水会蒸发，所以水位高度应高于底座上的切点0.5厘米。

第五步，拿出带有刻度的量筒，量出体积为100毫升的待测液在这个烧杯中的体积。

(1)极谱图的制作(2)基线图的制作(3)光谱图的制作，我们先观察第一张电导率表的标准曲线。

虽然实验中没有使用玻璃棒，但是由于定标点和量筒的原因，当然也包括在空气中，电导率值是不断减小的。

但是，如果再往量筒里加水，再观察电导率表的曲线就会发现，电导率值是不断增加的。

因为，电解时要有自由移动的电子参加反应，而电子运动会消耗能量，在减小的过程中，电子的能量变得越来越少，因而也就越来越难以到达测量电导率的点，所以曲线的斜率也就越来越大。

电导率和摩尔电导率与浓度关系的教学讨论
《电导率和摩尔电导率与浓度关系的教学讨论》
电导率是指电流密度与电势差的比值，它可以用来衡量溶液中电荷的传输能力。

摩尔电导率是指电导率与溶液的浓度的比值。

电导率和摩尔电导率与浓度有着密切的关系，随着溶液浓度的增加，电导率和摩尔电导率也会增加。

在教学中，我们可以用实验来说明电导率和摩尔电导率与浓度的关系。

可以让学生使用同种溶液，分别以不同的浓度制作几组样品，用电导仪测量每组样品的电导率，并记录下浓度和电导率的数据，用曲线图表示出来。

学生可以通过实验结果，直观地看出电导率和摩尔电导率与浓度的关系。

此外，还可以通过理论分析来说明电导率和摩尔电导率与浓度的关系。

因为溶液中的电荷随着浓度的增加而增加，所以电导率也会随之增加。

而摩尔电导率是电导率与浓度的比值，所以随着浓度的增加，摩尔电导率也会增加。

从实验和理论分析两个方面，我们可以清楚地看出电导率和摩尔电导率与浓度之间的关系，这有助于加深学生对电导率和摩尔电导率的理解。

无限稀溶液的摩尔电导
无限稀溶液是指溶液中溶质的浓度非常低，可以近似看作是无限小的溶液。

在这种情况下，溶液的电导率与溶质的浓度成正比，即溶质浓度越低，电导率越小。

而摩尔电导是指单位浓度的溶液的电导率，因此在无限稀溶液中，摩尔电导可以用来描述溶液的电导性质。

一、摩尔电导的定义
摩尔电导是指单位浓度的溶液的电导率，通常用符号Λ表示。

在国际单位制中，摩尔电导的单位是西门子·米/摩尔（S·m²/mol），其中西门子是电导率的单位，米是长度的单位，摩尔是物质的量的单位。

摩尔电导的计算公式为Λ = κ/c，其中κ是电导率，c是溶液的浓度。

二、在无限稀溶液中，溶质的浓度非常低，可以近似看作是无限小的溶液。

在这种情况下，溶液的电导率与溶质的浓度成正比，即溶质浓度越低，电导率越小。

因此，在无限稀溶液中，摩尔电导可以用来描述溶液的电导性质。

三、摩尔电导的应用
摩尔电导是描述溶液电导性质的重要参数，广泛应用于化学、生物、医学等领域。

在化学中，摩尔电导可以用来确定电解质的浓度和电离度，从而推断化学反应的平衡常数和反应机理。

在生物和医学中，摩尔电导可以用来测定生物体内的电解质浓度和离子交换，从而研究生
物体内的代谢和生理功能。

四、结论
无限稀溶液的摩尔电导是描述溶液电导性质的重要参数，可以用来推
断化学反应的平衡常数和反应机理，以及研究生物体内的代谢和生理
功能。

在实际应用中，需要注意溶液的浓度和温度对摩尔电导的影响，以保证测量结果的准确性。

外推法求极限摩尔电导率摩尔电导率是描述溶液中电导性的物理量，表示单位体积的溶液中的电导率。

摩尔电导率可以通过外推法来求解，外推法是一种数值计算方法，通过利用已知浓度范围内的电导率数据，预测未知浓度下的电导率。

在使用外推法求解摩尔电导率时，首先需要收集已知浓度范围内的电导率数据。

这些数据可以通过实验测量获得，或者是从文献中查找得到。

收集到的数据应该包括不同浓度下的电导率值，可以根据需要选择合适的浓度范围。

接下来，需要对收集到的电导率数据进行处理。

一种常用的处理方法是将浓度和对数电导率之间的关系进行线性化处理。

可以采用如下公式进行线性化处理：lg(κ) = a + b·lg(c)其中，κ表示电导率，c表示浓度，a和b为待求参数。

在数学上，可以使用最小二乘法来拟合出a和b的值，从而得到线性化的关系。

在得到线性化的关系后，就可以利用外推法进行计算了。

外推法是一种利用已知数据点外的数据点进行预测的方法。

在求解摩尔电导率时，我们可以利用线性化后的关系，通过已知的浓度范围外的浓度值，来预测对应的电导率值。

具体来说，我们可以选择一个较小的浓度值，通过线性化的关系计算出对应的对数电导率值。

然后，再通过反向计算，得到对应浓度下的摩尔电导率值。

需要注意的是，外推法的准确性和可靠性取决于所采用的线性化关系的合理性。

因此，在选择浓度范围和拟合参数时，需要进行合理的判断和选择，以保证外推结果的准确性。

总结起来，外推法是一种用于求解摩尔电导率的数值计算方法。

通过收集已知浓度范围内的电导率数据，进行线性化处理，并利用外推法进行预测，可以得到未知浓度下的摩尔电导率值。

在实际应用中，外推法可以用于溶液浓度的测定和溶解度的计算等领域。

第15卷　第3期大学化学2000年6月关于摩尔电导率的数学定义式孙　振　范(海南师范学院化学系　海口571158) 摩尔电导率Λm 是物理化学中的一个比较重要的概念。

I UPAC 建议的Λm 数学定义式不能完全反映Λm 的物理含义。

在使用过程中,特别是在不同的单位制一起使用时,Λm 的计算结果和单位与Λm 原始定义相背。

本文提出了一种新的Λm 数学定义式,该式更贴近Λm 原始定义,更能反映Λm 的物理含义。

1　电导和摩尔电导率 在物理化学中把电解质溶液的导电能力定义为: 定义1[1]:电导G =κ(A l )(1) G :电导(S ) κ:电导率(S ・cm -1或S ・m -1) A :电极的面积(cm 2或m 2) l :两电极间的距离(cm 或m ) 定义2[1]:摩尔电导率Λm 。

把含1m ol 电解质的溶液置于由相距为单位距离(SI 制用1m ,CG S 制用1cm )的两个平行电极板构成的电导池中,溶液所具有的电导称为该溶液的摩尔电导率。

如图1所示。

图1　摩尔电导率物理含义 由上面定义可知,Λm 实际上是特定条件下的G ,由于在定义Λm 时规定了电极板的距离为单位距离,因此在SI 单位制时的摩尔电导率(Λm )和CG S 单位制时的摩尔电导率(Λm ′)应是两个不同的物理量,它们应具有不同的值,也就是说,同是相同电解质相同浓度的含1m ol 电解质的溶液,在不同的极板距离时其导电能力是不一样的。

2　I UPAC 建议的Λm 数学定义式及其不足 I UPAC 所推荐的SI 单位制下Λm 的定义式为[1]: Λm =κ(1c )(2) (2)式的推导如下: Λm =κ(A m 1m )=κA m =κ(V m 1m )=κV m =κ(1c )25 在上面的推导过程中,两次把1略去不写的同时把其单位也略去不写。

如果使用CG S单位制同样也可做类似推导: Λm′=κ(A m1cm)=κA m=κ(V m1cm)=κV m=κ(1c)(2)′ 根据上述定义,Λm的单位为(S・m2・m ol-1或S・cm2・m ol-1),单位中的m2(或cm2)的物理含义不清楚,而且采用不同的单位制算出的Λm与Λm′相等,这与其原始定义不符,下面通过具体例子说明。