材料力学第7章-组合变形4+第9章-压杆稳定1-机械

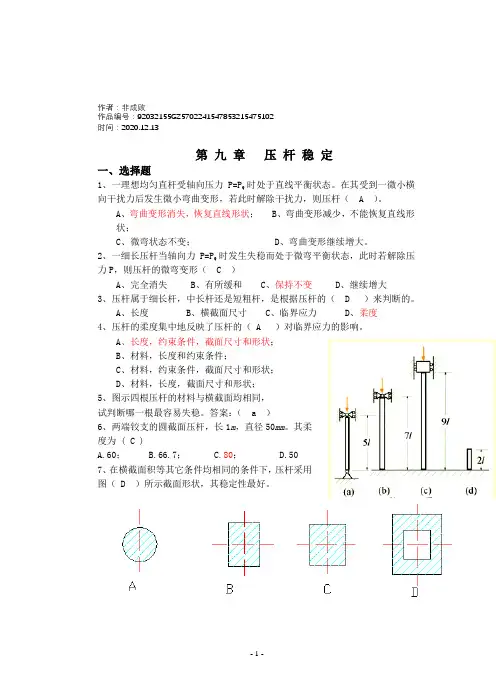
作者：非成败作品编号：92032155GZ5702241547853215475102时间：2020.12.13第九章压杆稳定一、选择题1、一理想均匀直杆受轴向压力P=P Q时处于直线平衡状态。

在其受到一微小横向干扰力后发生微小弯曲变形，若此时解除干扰力，则压杆（ A ）。

A、弯曲变形消失，恢复直线形状；B、弯曲变形减少，不能恢复直线形状；C、微弯状态不变；D、弯曲变形继续增大。

2、一细长压杆当轴向力P=P Q时发生失稳而处于微弯平衡状态，此时若解除压力P，则压杆的微弯变形（ C ）A、完全消失B、有所缓和C、保持不变D、继续增大3、压杆属于细长杆，中长杆还是短粗杆，是根据压杆的（ D ）来判断的。

A、长度B、横截面尺寸C、临界应力D、柔度4、压杆的柔度集中地反映了压杆的（ A ）对临界应力的影响。

A、长度，约束条件，截面尺寸和形状；B、材料，长度和约束条件；C、材料，约束条件，截面尺寸和形状；D、材料，长度，截面尺寸和形状；5、图示四根压杆的材料与横截面均相同，试判断哪一根最容易失稳。

答案：（ a ）6、两端铰支的圆截面压杆，长1m，直径50mm。

其柔度为 ( C )A.60；B.66.7；C.80；D.507、在横截面积等其它条件均相同的条件下，压杆采用图（ D ）所示截面形状，其稳定性最好。

8、细长压杆的（ A ），则其临界应力σ越大。

A 、弹性模量E 越大或柔度λ越小；B 、弹性模量E 越大或柔度λ越大；C 、弹性模量E 越小或柔度λ越大；D 、弹性模量E 越小或柔度λ越小； 9、欧拉公式适用的条件是，压杆的柔度（ C ）A 、λ≤、λ≤C 、λ≥π D、λ≥10、在材料相同的条件下，随着柔度的增大（ C ）A 、细长杆的临界应力是减小的，中长杆不是；B 、中长杆的临界应力是减小的，细长杆不是；C 、细长杆和中长杆的临界应力均是减小的；D 、细长杆和中长杆的临界应力均不是减小的； 11、两根材料和柔度都相同的压杆（ A ）A. 临界应力一定相等，临界压力不一定相等；B. 临界应力不一定相等，临界压力一定相等；C. 临界应力和临界压力一定相等；D. 临界应力和临界压力不一定相等；12、在下列有关压杆临界应力σe 的结论中，（ D ）是正确的。

材料力学章节重点和难点第一章绪论1．主要内容：材料力学的任务；强度、刚度和稳定性的概念；截面法、内力、应力，变形和应变的基本概念；变形固体的基本假设；杆件的四种基本变形。

2．重点：强度、刚度、稳定性的概念；变形固体的基本假设、内力、应力、应变的概念。

3．难点：第二章杆件的内力1．主要内容：杆件在拉压、扭转和弯曲时的内力计算；杆件在拉压、扭转和弯曲时的内力图绘制；平面弯曲的概念。

2．重点：剪力方程和弯矩方程、剪力图和弯矩图。

3. 难点：绘制剪力图和弯矩图、剪力和弯矩间的关系。

第三章杆件的应力与强度计算1．主要内容：拉压杆的应力和强度计算；材料拉伸和压缩时的力学性能；圆轴扭转时切应力和强度计算；梁弯曲时正应力和强度计算；梁弯曲时切应力和强度计算；剪切和挤压的实用计算方法；胡克定律和剪切胡克定律。

2．重点：拉压杆的应力和强度计算；材料拉伸和压缩时的力学性能；圆轴扭转时切应力和强度计算；梁弯曲时正应力和强度计算。

3．难点：圆轴扭转时切应力公式推导和应力分布；梁弯曲时应力公式推导和应力分布；第四章杆件的变形简单超静定问题1．主要内容：拉（压）杆的变形计算及单超静定问题的求解方法；圆轴扭转的变形和刚度计算；积分法和叠加法求弯曲变形；用变形比较法解超静定梁。

2．重点：拉（压）杆的变形计算；；圆轴扭转的变形和刚度计算；叠加法求弯曲变形；用变形比较法解超静定梁。

3．难点：积分法和叠加法求弯曲变形；用变形比较法解超静定结构。

第五章应力状态分析? 强度理论1．主要内容：应力状态的概念；平面应力状态分析的解析法和图解法；广义胡克定律；强度理论的概念及常用的四种强度理论。

2．重点：平面应力状态分析的解析法和图解法；广义虎克定律；常用的四种强度理论。

3．难点：主应力方位确定。

第六章组合变形1．主要内容：拉伸(压缩)与弯曲、斜弯曲、扭转与弯曲组合变形的强度计算；2．重点: 弯扭组合变形。

3．难点：截面核心的概念第七章压杆稳定1．主要内容：压杆稳定的概念；各种支座条件下细长压杆的临界载荷；欧拉公式的适用范围和经验公式；压杆的稳定性校核。

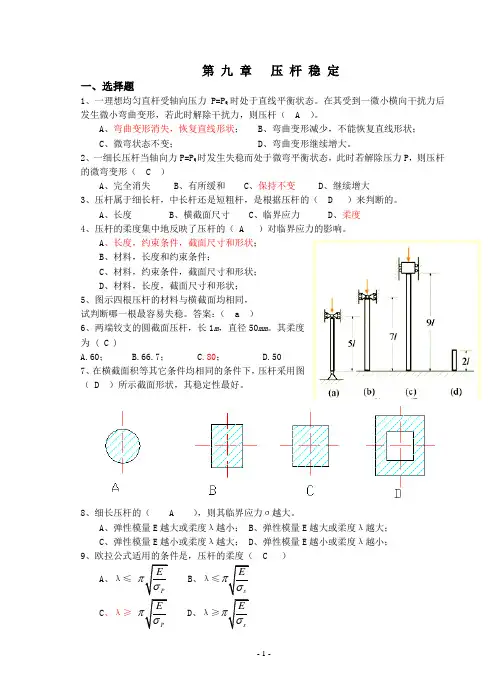
第 九 章 压 杆 稳 定一、选择题1、一理想均匀直杆受轴向压力P=P Q 时处于直线平衡状态。

在其受到一微小横向干扰力后发生微小弯曲变形，若此时解除干扰力，则压杆（ A ）。

A 、弯曲变形消失，恢复直线形状；B 、弯曲变形减少，不能恢复直线形状；C 、微弯状态不变；D 、弯曲变形继续增大。

2、一细长压杆当轴向力P=P Q 时发生失稳而处于微弯平衡状态，此时若解除压力P ，则压杆的微弯变形（ C ）A 、完全消失B 、有所缓和C 、保持不变D 、继续增大 3、压杆属于细长杆，中长杆还是短粗杆，是根据压杆的（ D ）来判断的。

A 、长度B 、横截面尺寸C 、临界应力D 、柔度 4、压杆的柔度集中地反映了压杆的（ A ）对临界应力的影响。

A 、长度，约束条件，截面尺寸和形状；B 、材料，长度和约束条件；C 、材料，约束条件，截面尺寸和形状；D 、材料，长度，截面尺寸和形状； 5、图示四根压杆的材料与横截面均相同， 试判断哪一根最容易失稳。

答案：（ a ）6、两端铰支的圆截面压杆，长1m ，直径50mm 。

其柔度为 ( C )A.60；B.66.7； C .80； D.50 7、在横截面积等其它条件均相同的条件下，压杆采用图（ D ）所示截面形状，其稳定性最好。

8、细长压杆的（ A ），则其临界应力σ越大。

A 、弹性模量E 越大或柔度λ越小；B 、弹性模量E 越大或柔度λ越大；C 、弹性模量E 越小或柔度λ越大；D 、弹性模量E 越小或柔度λ越小； 9、欧拉公式适用的条件是，压杆的柔度（ C ）A 、λ≤ PEπσ B 、λ≤sEπσC 、λ≥ P Eπσ D 、λ≥sEπσ10、在材料相同的条件下，随着柔度的增大（ C ）A 、细长杆的临界应力是减小的，中长杆不是；B 、中长杆的临界应力是减小的，细长杆不是；C 、细长杆和中长杆的临界应力均是减小的；D 、细长杆和中长杆的临界应力均不是减小的； 11、两根材料和柔度都相同的压杆（ A ）A. 临界应力一定相等，临界压力不一定相等；B. 临界应力不一定相等，临界压力一定相等；C. 临界应力和临界压力一定相等；D. 临界应力和临界压力不一定相等；12、在下列有关压杆临界应力σe 的结论中，（ D ）是正确的。

第九章 压杆稳定§9-1 压杆稳定性的概念一、引言工程中有许多细长的轴向压缩杆件，例如，气缸或油缸中的活塞杆、内燃机连件、建筑结构中的立柱、火箭的级间连接支杆等。

材料力学中统称为压杆或柱。

前面研究直杆轴向压缩时，认为杆是在直线形态下维持平衡，杆的失效是由于强度不足而引起的。

事实上，这样考虑，只对短粗的压杆才有意义，而对细长的压杆，当它们所受到的轴向外力远未达到其发生强度失效时的数值，可能会突然变弯而丧失了原有直线形态下的平衡而引起失效。

它是不同于强度失效的又一种失效形式。

受压变弯的原因：（1）压秆在制造时其轴线存在初曲率。

（2）合外力作用线与杆轴线没有重合。

（3）材料的不均匀性。

二、“中心受压理想直杆”力学模型及稳定的概念力学模型：材料绝对理想；轴线绝对直；压力绝对沿轴线作用 试验：取如图所示两端铰支均质等直细长杆，加轴向压力F ，压杆呈直线形态平衡。

现在，若此压杆受到一很小的横向干扰力。

(例如，轻轻地推一下)，则压杆弯曲，如图 a 中虚线所示。

当横向干扰力解除后，会出现下述两种情况：1) 当轴向压力F 小于某一数值时，压杆又恢复到原来的直线平衡形态，如图 b 所示。

（稳定平衡） 2) 当轴向压力F 增加到这一数值时，虽然干扰力已解除，但压杆不再恢复到原来的直线平衡形态，而在微弯曲的形态下平衡，如图 c 所示。

（不稳定平衡）可见，压杆的原来直线形态平衡是否稳定，与所受轴向压力F 的大小有关；当轴向压力F 由小逐渐增加到某一个数值时，压杆的直线形态平衡由稳定过渡到不稳定。

压杆的直线形态平衡由稳定过渡到不稳定所受的轴向压力的界限值，称为压杆的临界力，用F cr 表示。

当压杆所受的轴向压力F 达到临界力F cr 时，其直线形态的平衡开始丧失，我们称压杆丧失了稳定性，简称失稳。

研究压杆稳定性的关键是寻求其临界力的值。

§9-2细长中心受压直杆临界力的欧拉公式假设两端球形铰支的等直细长压杆所受的轴向压力刚好等于其临界力，并且已经失稳而在微弯曲状态下保持平衡，如图所示。

【陆工总结材料力学考试重点】之（第7章）压杆的稳定性问题1、压杆稳定性的特点？答：1）杆件两端受轴向压缩载荷作用；2）杆子比较细长；3）产生弯曲变形。

2、细长压杆的平衡状态？答：在F的作用下，压杆存在两种平衡状态：直线平衡状态，弯曲平衡状态。

F cr称为临界载荷，即使杆件恰好由直杆变为曲杆的压缩载荷。

压杆稳定性问题的关键就是求临界载荷F cr。

3、细长压杆的临界载荷——欧拉公式？答：细长压杆的临界载荷公式（欧拉公式）：F cr=π2EI (μL)2式中：L为压杆的实际长度，μ为长度系数，μL为压杆的相当长度（有效长度），I为压杆横截面对中性轴的惯性矩，E为弹性模量。

注意：对于上图所示矩形截面压杆，有两种弯曲可能，在xz面弯曲，或yx面弯曲，具体在哪个面弯曲，取决于惯性矩I z=bℎ312和I y=ℎb312的大小。

若I y>I z，则在xz平面内弯曲；若I z>I y，则在xy平面内弯曲；即采用F cr=π2EI(μL)2计算细长压杆的临界载荷时，I取I y、I z里面的较小值。

4、不同约束的长度系数μ值？1）对于图a）：细长压杆的一端为固定端约束，一端为自由端，μ=2 2）对于图b）：细长压杆的两端均为铰链约束，μ=13）对于图c）：细长压杆的一端为固定端约束，一端为铰链约束，μ=0.7 4）对于图d）：细长压杆的两端均为固定端约束， μ=0.5约束的强弱程度顺序：固定端约束>铰链约束>自由端约束可知：约束程度越强，则μ值越小。

5、临界正应力总图？答：根据不同压杆临界正应力σcr与长细比λ之间的关系绘成图，即可得到压杆的临界正应力总图：结论：杆子长细比λ越大，临界正应力σcr（临界载荷F cr=σcr A）越小，则杆子越容易弯曲（实际经验也可知道，杆子越细越长，则越容易被压弯）。

6、压杆的稳定性计算？答：设压杆的临界载荷为F cr，压杆实际承受的工作载荷为F，定义安全系数：n=F crF（可知，对于固定的压杆，其临界载荷为一固定值，则实际承受的工作载荷越小，安全系数就越大，压杆也就越安全），出于工程安全的考虑，假设压杆所允许的工作安全系数为[n]st（大于1的数），则实际操作中就必须满足：n=F crF≥[n]st。