第五章傅里叶变换光学
- 格式:pdf
- 大小:1.32 MB
- 文档页数:25

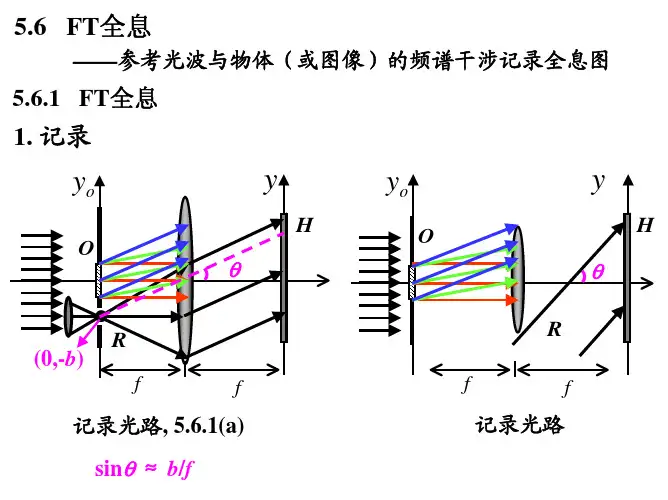

傅里叶变换光学LT22012111(,)()()2D x y D x y R R =-+-(4)其中1R 、2R 是构成透镜的两个球面的曲率半径。
公式(4)对双凹、双凸、或凹凸透镜都成立。
引入焦距f ,其定义为:12111(1)()n f R R=-- (5)代入(3)得: 220(,)exp()exp[()]2k t x y jknD j xy f =-+(6)式(6)即是透镜位相调制的表达式,它表明复振幅(,)LU x y 通过透镜时,透镜各点都发生位相延迟。
从式(6)容易看出第一项位相因子0exp()jknD 仅表示入射光波的常量位相延迟,不影响位相的空间分布,即波面形状,所以在运算过程中可以略去。
第二项22exp[()]2k j xy f -+是具有调制作用的因子,它表明光波通过透镜的位相延迟与该点到透镜中心的距离的平方成正比。
而且与透镜的焦距有关。
当考虑透镜孔径后,有:22(,)exp[()](,)2kt x y jx y p x y f=-+(7)其中的(,)p x y 为透镜的光瞳函数,表达式为: 1(,)0p x y ⎧=⎨⎩ 孔径内其 它(8)2、透镜的傅里叶变换性质在单色平面波垂直照射下,夫琅和斐衍射光场的复振幅分布正比于衍射屏透射系数的傅里叶变换。
衍射图像的强度分布正比于衍射屏的功率谱分布。
一般情况下,我们是将夫朗和斐衍射图像成像到透镜的像方焦平面出,这就是说,作为成像元件的透镜,就相当于傅里叶变换器。
如图2所示,设单位振幅的单色平面光垂直照射一透射系数为(,)t x y 的衍射屏,与衍射屏相距Z 处放置一焦距为f 的薄透镜L ,先观察其像方平面L 的光场分布。
为了讨论方便,这里我们忽略透镜材料的吸收、散射、透镜表面的反射以及透镜孔径大小等因素的影响。
图2 透镜的傅里叶变换性质设(,)E x y 、11E(,)x y 、11E (,)x y '、(,)ffE x y 分别表示衍射屏后、透镜输入平面、输出平面以及像方平面出光波场的复振幅分布。

光学傅里叶变换原理傅里叶变换是一种数学工具,用于将一个函数( 或信号)从时间 或空间)域转换到频率域。
在光学中,傅里叶变换也具有重要的应用,尤其是在描述光波传播、光学系统和图像处理等方面。
傅里叶变换原理涉及到以下重要概念和原则:1.(傅里叶级数:傅里叶级数指的是将周期性函数分解为一系列正弦和余弦函数的和的过程。
它表明任何周期性函数都可以表示为不同频率的正弦和余弦函数的叠加。
2.(连续傅里叶变换 Continuous(Fourier(Transform):对于连续信号,傅里叶变换将信号从时域转换到频域。
它描述了信号在频率空间中的频谱特性,展示了信号由哪些频率分量组成。
3.(离散傅里叶变换 Discrete(Fourier(Transform):对于离散数据集合,比如数字图像或采样信号,离散傅里叶变换用于将这些离散数据从时域转换到频域。
它在数字信号处理和图像处理中得到广泛应用,用于分析和处理频率特性。
4.(光学中的应用:在光学中,傅里叶变换可以描述光的传播和衍射现象。
例如,傅里叶光学理论表明,光学系统(如透镜、光栅等)可以看作是对光波进行空间域的傅里叶变换。
这种理论有助于理解光的传播特性,并在光学系统设计和成像技术中发挥重要作用。
5.(变换原理:傅里叶变换原理表明,任何一个信号都可以通过傅里叶变换分解成一系列不同频率的正弦和余弦函数。
这种变换可以帮助我们理解信号的频率成分,并对信号进行处理、滤波或合成。
总的来说,傅里叶变换原理提供了一种从时域到频域的转换方法,在光学中,它被广泛应用于光波传播、光学系统设计和图像处理等领域,为我们理解和处理光学现象提供了重要的工具。

第5章广义傅里叶变换及其光学实现广义傅里叶变换(Generalized Fourier Transform)是一种在信号处理和光学领域中广泛使用的数学工具,它能够将一个信号从时域(时间域)转换到频域(频率域),或者反之。
广义傅里叶变换不仅可以用于分析信号的频谱特性,还可以用于信号的滤波、去噪、编码等方面。
广义傅里叶变换可以看作是傅里叶级数的推广。
在傅里叶级数中,我们将周期信号表示为一系列正弦和余弦函数的和,其中每个正弦和余弦函数的频率是信号频谱中的一个成分。
而在广义傅里叶变换中,我们可以处理非周期信号,将其转换为连续的频谱函数。
广义傅里叶变换的公式如下:\begin{gather*}F(k) = \int_{-\infty}^{+\infty} f(x) \cdot e^{-2\pi j k x}dx \\f(x) = \int_{-\infty}^{+\infty} F(k) \cdot e^{2\pi j k x} dk \end{gather*}其中,$f(x)$是信号在时域中的函数,$F(k)$是信号在频域中的函数,$j$是虚数单位。
广义傅里叶变换通过对信号在时域和频域中的函数进行积分,将信号在两个域之间进行转换。
广义傅里叶变换在光学实现中也有广泛应用。
例如,光的干涉实验中,我们可以将光通过一个透镜汇聚到光阑上,并在光阑上形成一个干涉图样。
通过对这个干涉图样进行广义傅里叶变换可以得到光的频谱特性,进而分析光的波长、频率等参数。
另外,广义傅里叶变换还可以用于光信号的编码和解码,例如光通信领域中的光码分复用技术(Optical Code Division Multiple Access,OCDMA)。
广义傅里叶变换的光学实现通常采用光学透镜、空间光调制器等光学元件。
通过光学透镜,我们可以将光信号汇聚到光阑上,在光阑上形成干涉图样;而空间光调制器可以用于调制干涉图样中的光场,实现对干涉信号的频域处理。
第五章 光学成像系统的频率特性传统的光学系统像质评价方法是星点法和分辨率法。
光学成像系统是信息传递的系统。
输出像的质量完全取决于光学系统的传递特性。
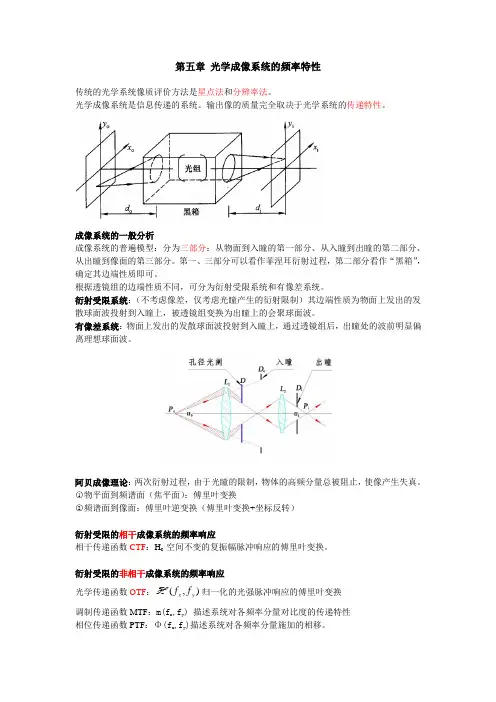
成像系统的一般分析成像系统的普遍模型:分为三部分:从物面到入瞳的第一部分、从入瞳到出瞳的第二部分、从出瞳到像面的第三部分。
第一、三部分可以看作菲涅耳衍射过程,第二部分看作“黑箱”,确定其边端性质即可。
根据透镜组的边端性质不同,可分为衍射受限系统和有像差系统。
衍射受限系统:(不考虑像差,仅考虑光瞳产生的衍射限制)其边端性质为物面上发出的发散球面波投射到入瞳上,被透镜组变换为出瞳上的会聚球面波。
有像差系统:物面上发出的发散球面波投射到入瞳上,通过透镜组后,出瞳处的波前明显偏离理想球面波。
阿贝成像理论:两次衍射过程,由于光瞳的限制,物体的高频分量总被阻止,使像产生失真。
○1物平面到频谱面(焦平面):傅里叶变换○2频谱面到像面:傅里叶逆变换(傅里叶变换+坐标反转)衍射受限的相干成像系统的频率响应相干传递函数CTF :H c 空间不变的复振幅脉冲响应的傅里叶变换。
衍射受限的非相干成像系统的频率响应光学传递函数OTF :),(y x f f H 归一化的光强脉冲响应的傅里叶变换调制传递函数MTF :m(f x ,f y ) 描述系统对各频率分量对比度的传递特性相位传递函数PTF :Φ(f x ,f y )描述系统对各频率分量施加的相移。
()()()y x y x y x f f j f f m f f ,ex p ,),(Φ=H光曈总面积重叠面积=),(y x f f H H 的几何解释为两个错开光瞳函数相互重叠面积占光瞳总面积的比例。
像差对成像系统传递函数的影响广义光瞳函数()()(),exp ,,P jkW P ξηξηξη=⎡⎤⎣⎦%像差对CTF 的影响:通频带内引入位相畸变,使像质变坏。
像差对OTF 的影响:使各空间频率余弦分量的调制度进一步下降,各频率分量有相对相移,使成像质量下降。
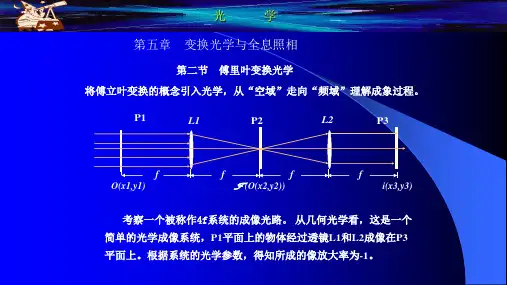



第五章傅里叶变换光学与相因子分析方法5.1 衍射系统 波前变换◆引言现代光学的重大进展之一,是引入“光学变换”概念,由此发展而形成了光学领域的一个新分支——傅里叶变换光学,泛称为变换光学(transform optics),也简称为博里叶光学,它导致了光学信息处理技术的兴起.现代变换光学是以经典波动光学的基本原理为基础,是干涉、衍射理论的综合和提高,它与衍射、尤其与夫琅禾费衍射息息相关.对于熟悉经典波动光学的人们来说,由于他们有着较充分的概念储备和较充实的物理图像,因而具备更为有利的条件,去深刻而灵活地掌握现代变换光学. ◆衍射系统及其三个波前如图所示,一个衍射系统以衍射屏为界被分为前后两个空间.前场为照明空间,充满照明光波;后场为衍射空间,充满衍射光波.照明光波比较简单、常为球面波或平面波,这两种典型波的等幅面与等相面是重合的,属于均匀波,其波场中没有因光强起伏而出现的图样.衍射波较为复杂,它不是单纯的一列球面波或一列平面波,其等幅面与等相面—般地不重合,属于非均匀波,其波场中常有光强起伏而形成的衍射图样.在衍射系统的分析中,人们关注三个场分布:其中,入射场),(~1y x U 是照明光波到达衍射屏的波前函数;出射场),(~2y x U 是衍射屏的透射场或反射场,它是衍射空间初端的波前函数,它决定了整个衍射空间的光场分布;而衍射场),(~y x U ''是纵向特定位置的波前函数。
由此可见,整个衍射系统贯穿着波前变换:波前),(~),(~21y x U y x U →这是衍射屏的作用: 波前),(~),(~2y x U y x U ''→这是波的传播行为.由一个波前导出前方任意处的另一个波前,这是波衍射问题的基本提法,亦即波传播问 题的基本提法.标量波的传播规律己由惠更斯—菲涅耳—基尔霍夫理论(HFK 理论)给出.在 常见的傍轴情形下,其表达式为其积分核为ikre,这是一个球面波的相因子形式.换言之HFK 理论是—个关于衍射的球面波理论——衍射场是衍射屏上大量次波点源所发射的球面被的相干叠加.◆衍射屏函数及其三种类型我们已经同多种衍射屏有过交道,现在给山衍射屏函数的一般性定义,以定量地描述衍射屏的自身特征:),(12),(),(~),(~),(~y x i ey x t y x U y x U y x t ϕ== 即,屏函数(screen function)等于出射波前函数与入射波前函数之比.对于透射屏,t ~可称作复振幅透过率函数;对于反射屏,t ~可称作复振幅反射率函数.无疑,屏函数通常也是复函数,含模函数),(y x t 和辐角函数),(y x ϕ.唯象地看,实际上的衍射屏可分为三种类型,振幅型、相位型和相幅型.若),(y x ϕ为常数,仅有函数),(y x t ,则该衍射屏为振幅型,凡孔型衍射屏均系振幅型.若),(y x t 为常数,仅有函数),(y x ϕ,则该衍射屏为相位型,这在此之前似乎少见,其实,闪耀光栅不论其为透射的或反射的,均是一个相位型衍射屏,下一节即将研究的透镜相位衍射元件.当然,更为一般的情况是相幅型衍射屏,),(y x t 、),(y x ϕ皆为函数形式,即不仅出射场的振幅分布),(2y x A 有别于入射场的),(1y x A ,而且出射场的相位分布),(2y x ϕ也有别于入射场的),(1y x ϕ。
傅里叶光学变换
傅里叶光学变换是一种将光学信号从时域转换到频域的数学工具。
它通过将光学信号分解为不同的频率成分,可以帮助我们更好地理解和分析光学现象。
傅里叶光学变换基于傅里叶变换的原理,在光学领域广泛应用于光波的传播、衍射和成像等问题。
通过傅里叶光学变换,我们可以把一个光学信号表示为一系列不同频率的正弦波的叠加,这些正弦波的振幅和相位信息可以提供有关原始信号的详细特征。
傅里叶光学变换的数学公式如下:
F(ν) = ∫f(t)e^(-2πiνt)dt
其中,F(ν)表示频率为ν的光学信号的傅里叶变换结果,f(t)表示原始光学信号,e为自然对数的底。
傅里叶光学变换的一个重要应用是光学成像。
通过将光场的复振幅进行傅里叶变换,可以获得物体的光学频谱信息,从而实现对物体的高分辨率成像。
此外,傅里叶光学变换还可以应用于光衍射、光波前传播和信号处理等方面。
通过分析不同频率成分的振幅和相位信息,我们可以了解光场在不同空间位置和时间点的变化规律,从而对光学现象进行更深入的研究。
总之,傅里叶光学变换是光学领域中一种重要的数学工具,它能够帮助我们从频域的角度来理解和分析光学信号的特性和行为,为光学研究和应用提供了有力的支持。