光信息专业实验：傅里叶光学变换系统 1 中山大学光信息专业实验报告：傅里叶光学变换系统 实验人：何杰勇（11343022） 合作人：徐艺灵 组号B13 一、实验目的和内容 1、了解透镜对入射波前的相位调制原理。 2、加深对透镜复振幅、传递函数、透过率等参量的物理意义的认识。 3、观察透镜的傅氏变换（FT）图像，观察4f系统的反傅氏变换（IFT）图像，并进行比较。 4、在4f系统的变换平面（T）插入各种空间滤波器，观察各种试件相应的频谱处理图像。
二、实验原理 1、透镜的FT性质及常用函数与图形的关学频谱分析 透镜由于本身厚度的不同，使得入射光在通过透镜时，各处走过的光程差不同，即所受时间延迟不同，因而具有相位调制能力。图1 为简化分析，假设任意点入射光线在透镜中的传播距离等于改点沿光轴方向透镜的厚度，并忽略光强损失，即通过透镜的光波振幅分布不变，仅产生位相的变化，且其大小正比于透镜在该
点的厚度。设原复振幅分布为(,)LUxy的光通过透镜后，其复振
幅分布受到透镜的位相调制，附加了一个位相因子(,)xy后变为(,)LUxy： 图1 (,)(,)exp[(,)]LLUxyUxyjxy
（1）
若对于任意一点（x，y）透镜的厚度为(,)Dxy，透镜的中心厚度为0D
。光线由该点通
过透镜时在透镜中的距离为(,)Dxy，空气空的距离为0D－(,)Dxy，透镜折射率为n，则该点的总的位相差为： 00(,)[(,)](,)(1)(,)xykDDxyknDxykDknDxy （2）
（2）中的k＝2π/λ，为入射光波波数。 用位相延迟因子(,)txy来表示即为：
0(,)exp()exp[(1)(,)]txyjkDjknDxy （3）
由此可见只要知道透镜的厚度函数(,)Dxy就可得出其相位调制。在球面镜傍轴区域，用抛物面近似球面，可以得到球面透镜的厚度函数为：
Q1 D(x,y) M N Q2
D0 光信息专业实验：傅里叶光学变换系统
2 22012
111(,)()()2DxyDxyRR （4）
其中1R、2R是构成透镜的两个球面的曲率半径。公式（4）对双凹、双凸、或凹凸透镜都成立。引入焦距f，其定义为：
12111(1)()nfRR （5）
代入（3）得： 220(,)exp()exp[()]2ktxyjknDjxyf （6） 式（6）即是透镜位相调制的表达式，它表明复振幅(,)LUxy通过透镜时，透镜各点都发生位相延迟。 从式（6）容易看出第一项位相因子0exp()jknD
仅表示入射光波的常量位相延迟，不影
响位相的空间分布，即波面形状，所以在运算过程中可以略去。第二项22exp[()]2kjxyf
是具有调制作用的因子，它表明光波通过透镜的位相延迟与该点到透镜中心的距离的平方成正比。而且与透镜的焦距有关。当考虑透镜孔径后，有：
22(,)exp[()](,)2ktxyjxypxyf
（7）
其中的(,)pxy为透镜的光瞳函数，表达式为： 1(,)0pxy 孔径内 其 它 （8）
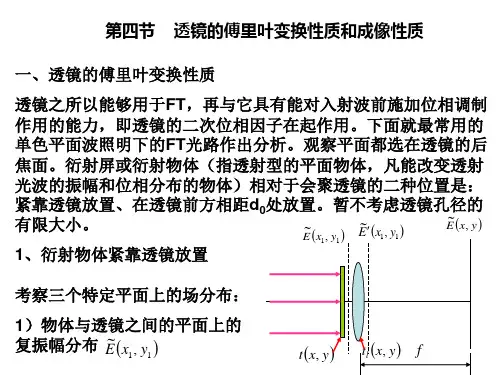
2、透镜的傅里叶变换性质 在单色平面波垂直照射下，夫琅和斐衍射光场的复振幅分布正比于衍射屏透射系数的傅里叶变换。衍射图像的强度分布正比于衍射屏的功率谱分布。一般情况下，我们是将夫朗和斐衍射图像成像到透镜的像方焦平面出，这就是说，作为成像元件的透镜，就相当于傅里叶变换器。 如图2所示，设单位振幅的单色平面光垂直照射一透射系数为(,)txy的衍射屏，与衍射屏相距Z处放置一焦距为f的薄透镜L，先观察其像方平面L的光场分布。为了讨论方便，这里我们忽略透镜材料的吸收、散射、透镜表面的反射以及透镜孔径大小等因素的影响。 光信息专业实验：傅里叶光学变换系统 3 图2 透镜的傅里叶变换性质 设(,)Exy、11E(,)xy、11E(,)xy、(,)ffExy分别表示衍射屏后、透镜输入平面、输出平面以及像方平面出光波场的复振幅分布。由于透镜的相位调制特性，输出平面与输入平面出光波场之间的关系由下式决定：
221111E(,)E(,)exp[()]2kxyxyixyf
（9）
而从透镜输出平面到像方焦平面，光波相当于经历一次菲涅耳衍射。夫朗和斐近似下观察到平面上的衍射光场复振幅 ：
222210011
1111
()()2()0011111(,)E(,)izizikzxyxyzzizuxvyeExyexyeedxdyiz
＝22100
1
()22111111{E(,)exp[()]}izikzxyzeeFxyixyizz
（10）
式中u和v分别表示1x和1y
方向的空间频率。于是由（9）和（10）式，透镜像方焦平
面上的光波场复振幅(,)ffExy分布应具有如下形式： 2222
21111(,){E(,)exp()}2ffxyikfikfff
xyeExyeFxyikiff
＝22211{E(,)}ffxyikfikfeeFxyif （ ,ffxyuvff ） （11）
在单位振幅的平面波垂直照射下，透镜衍射屏的光波场复振幅分布(,)Exy即等于衍射屏的透射系数(,)txy，故其频谱分布为： {(,)}{(,)}(,)FExyFtxyTuv （12） 光信息专业实验：傅里叶光学变换系统 4 该频谱分量从衍射屏传播到透镜的输入平面处，产生一个相位延迟(,,)uvz，即有： (,)(,)exp[(,,)]EuvTuviuvz （13）
在傍轴条件下(,,)uvz具有如下的形式： 222(,,)()2kuvzkzzuv （14）
由此可以得到透镜输入平面处光波场的频谱分布为：
22211{(,)}(,)(,)exp[()]2kFExyEuvTuvikzizuv
（15）
代入（11）得透镜像方焦平面处的广场分布为： 222222(,)exp[()](,)2ffxyikfikf
ff
ekExyeikzizuvTuvif
＝22()(1)2(,)ffxyzikzfikffeeTuvif （,ffxyuvff） （16）
从上式可以看到，在单色平面波垂直照射下，透镜像方焦平面处的光场除了一个常数因子外和一个二次因子外，其余的反应了衍射屏透射系数得傅里叶变换。经过进一步的分析我们可以得到在用透镜对二维关学图像进行傅里叶变换时，若将图像放置在透镜的物方焦平面上，则在透镜的像方焦平面上得到输入图像准确的傅里叶变换。若将输入图像放置在透镜与其像方焦平面之间，则像方焦平面上频谱图样的大小可随衍射屏到像方焦平面的距离的变化而改变；并且当输入图像紧贴透镜后放置时可获得最大的频谱图样。而对于球面波照射时，傅里叶变换平面将不是在透镜的像方平面。而是光源的共轭像平面上。
3．透镜孔径的衍射与滤波特性 由于孔径的衍射效应，任何具有有限大小通过光孔径的光学成像系统，均不存在如几何光学中所说的理想像点。所谓共轭像点，实际上是由系统孔径引起的，以物点的几何像点为中心的夫琅和斐衍射图样的中央亮斑——艾里斑。其次，透镜有限大小的通光孔径，也限制了衍射屏函数的较高频率成分（具有较大入射倾角的平面波分量）的传播。这可以从图3可以看出：
图3：透镜孔径引起渐晕效应 光信息专业实验：傅里叶光学变换系统
5 透过衍射屏的基频平面波分量1可以全部通过透镜，具有较高（空间）频率的平面波分量2只能部分通过，而高频平面波分量3则完全不能通过。这样，在透镜像方焦平面上的光波场中就缺少了衍射屏透射光场中部分高频成分，因此，所得衍射屏函数的频谱将不完整。这种现象称为衍射的渐晕效应。由此可将，从光信息处理角度来讲，透镜孔径的有限大小，使得系统存在着有限大小的通频宽带和截止频率；从光学成像的角度来讲，则使得系统存在着一个分辨极限。 4．相干光学图像处理系统（4f系统） 用夫琅和斐衍射来实现图像的频谱分解，最重要的意义是为空间滤波创造了条件，由
于衍射场就是屏函数的傅里叶频谱面，空间频率（u，v）与衍射场点位置（,）一一对应，使得人们可见从改变频谱入手来改造图像，进行信息处理。为此，设计了图4所示的图像处理系统。
图4 4f图像处理系统 在此系统中，两个透镜1L、2L成共焦组合，1L的前焦面（x，y）为物平面O，图像由
此输入，2L的后焦面(',')xy为像平面I，图像在此输出。共焦平面（,）称为变换平面T，在此可以安插各种结构和性能的屏（即空间滤波器）。 当平行光照射在物平面上时，整个OTI系统成为相干成像系统。由于变换平面上空间滤波器的作用，使输出图像得以改造，所以OTI系统又是一个相干光学信息处理系统。这里先研究它的成像问题。 我们将相干光学系统的成像过程看作两步：第一步，从O面到T面，使第一次夫琅和斐衍射，它起分频作用。第二步，从T面到I面，再次夫琅和斐衍射，起合成作用，即综合频谱输出图像。在这样的两步中，变换平面T处于关键地位，若在此处设置光学滤波器，就能起到选频作用。要想作到图像的严格复原，T面必须完全畅通无阻。此处的4f系统每次衍射都是从焦面到焦面，这就保证了复振幅的变换是纯粹的傅里叶变换。如果光波能够自由通过变换平面，即连续两次的傅里叶变换，函数的形式基本复原，只是自变量变号,
),(),(01yxUyxU即图像倒置。在有源滤波器的情况下,001UtUUT这里为滤波
器的透过率函数，这也是我们进行滤波实验的依据。
