数学分析课件 平面点集与多元函数

数学分析16.1平面点集与多元函数第十六章多元函数的极限与连续1平面点集与多元函数一、平面点集概念1：在平面上确定一个坐标系(一般指平面直角坐标系)，所有有序实数对(x,y)与平面上所有的点之间建立了一一对应，因此“数对”可等同于“平面上的点”，这种确定了坐标系的平面称为坐标平面. 坐标平面上满足某种条件P的点的集合称为平面点集，记作：E={(x,y)|(x,y)满足条件P}.如R2={(x,y)|-∞<x<+∞,-∞<=""></x<+∞,-∞以原点为中心，r为半径的圆内所有点的集合是C={(x,y)|x2+y2<="" p="">一般地，对于任意两个数集A, B，记A×B={(x,y)|x∈A,y∈B }，称为A 与B的直积. 如：A={(u,v)|u2+v2<1}，B=[0,1]，则A×B={(u,v,w)|u2+v2<1, 0≤w≤1 }.平面点集{(x,y)|(x-x0)2+(y-y0)2<δ2}与{(x,y)||x-x0|<δ,|y-y0|<δ}分别称为以点A(x0,y0)为中心的δ圆邻域与δ方邻域.点A的任一圆邻域可包含在点A的某一方邻域之内(反之亦然)，所以通常用“点A的δ邻域”或“点A的邻域”泛指这两种形状的邻域，并记为U(A;δ)或U(A). 而点A的空心邻域是指：(记为U?(A;δ)或U?(A)) {(x,y)|0<(x-x0)2+(y-y0)2<δ2}或{(x,y)||x-x0|<δ,|y-y0|<δ, (x,y)≠(x0,y0)}.任一点A∈R2与任意一个点集E?R2之间必有以下三种关系之一：1、内点：若存在点A的某邻域U(A)，使得U(A)?E，则称A是点集E 的内点. E的全体内点构成的集合称为E的内部，记作int E.2、外点：若存在点A的某邻域U(A)，使得U(A)∩E=?，则称A 是点集E的外点.3、界点：若点A的任何邻域内既含有属于E的点，又含有不属于E 的点，则称A是集合E的界点. 即对任何正数δ，恒有U(A;δ)∩E≠?且U(A;δ)∩E c≠?，其中E c=R2\E是E关于全平面的余集. E的全体界点构成E的边界，记作?E.内点属于E，外点不属于E，界点不能确定.按点A的近旁是否密集着E中无穷多个点而构成的关系：1、聚点：若在点A的任何空心邻域U?(A)内都含有E中的点，则称A 是E的聚点. 聚点不一定属于E. A是点集E的聚点的定义等价于“点A的任何邻域U(A)内包含有E的无穷多个点”.2、孤立点：若点A∈E, 但不是E的聚点，即存在某一正数δ，使得U?(A;δ)∩E=?，则称点A是E的孤立点. 孤立点一定是界点，内点和非孤立的界点一定是聚点，即不是聚点，又不是孤立点，必为外点.例1：设平面点集D={(x,y)|1≤x2+y2<4}，分别指出它的内点、界点和聚点，并指出界点是否属于点集D.解：满足1<x2+y2<4的一切点都是d的内点；< bdsfid="88" p=""></x2+y2<4的一切点都是d的内点；<>满足x2+y2=1的一切点是D的界点且属于D；满足x2+y2=4的一切点是D的界点且不属于D；点集D连同它外圆边界上的所有点都是D的聚点.概念2：重要的平面点集：1、开集：若平面点集所属的每一点都是E的内点(即intE=E)，则称E 为开集.2、闭集：若平面点集E的所有集点都属于E，则称E为闭集. 没有聚点的点集也称为闭集.注：例1中的点集D即不是开集也不是闭集；R2和?既开又闭.3、开域：若非空开集E具有连通性，即E中任意两点之间都可用一条完全包含于E的有限折线相连接，则称E为开域(非空连通开集).4、闭域：开域连同其边界所成的点集称为闭域.5、区域：开域、闭域，或者开域连同其一部分界点所成的点集，统称为区域. 反例：开集E={(x,y)|xy>0}在I,III象限之间不具有连通性，所以它不是区域.6、有界点集：对于平面点集E，若存在某一正数r ，使得E?U(O,r)，其中O 为坐标原点(也可为其它固定点)，则称E 为有界点集. 反之则为无界点集. E 为有界点集等价于：存在矩形区域D=[a,b]×[c,d]?E.点集的有界性可用点集的直径来反映，即d(E)=EP ,P 21sup ∈ρ(P 1,P 2)，其中ρ(P 1,P 2)表示P 1与P 2两点之间的距离，当P 1,P 2的坐标分别为(x 1,y 1)和(x 2,y 2)时，则ρ(P 1,P 2)=221221)-y (y )x -(x +，于是当d(E)为有限值时，E 为有界点集.根据距离的概念，对R 2上的任意三点P 1,P 2,P 3，有以下三角不等式：ρ(P1,P 2)≤ρ(P 1,P 3)+ ρ(P 2,P 3).例2：证明：对任何S ?R 2，?S 恒为闭集.证：如图：设x 0为?S 的任一聚点，ε>0，由聚点的定义，?γ∈U ?(x 0;ε)∩?S. 又γ是S 的界点，∴对任意U(γ;δ)?U ?(x 0;ε), U(γ;δ)上既有S 的点，又有非S 的点. ∴U(x 0;ε)上也既有S 的点，又有非S 的点，即x 0∈?S ，∴?S 恒为闭集.二、R 2上的完备性定理定义1：设{P n }?R 2为平面点列，P 0∈R 2为一固定点. 若对任给的正数ε，存在正整数N ，使得当n>N 时，有P n ∈(P 0;ε)，则称点列{P n }收敛于点P 0，记作：∞→n lim P n =P 0或P n →P 0, n →∞.注：分别以(x n ,y n )与(x 0,y 0)表示P n 与P 0时，∞→n lim P n =P 0等价于∞→n lim x n =x 0，∞→n lim y n =y 0. 以ρ(P 1,P 2)表示P n 与P 0之间距离时，∞→n lim P n =P 0又等价于，∞→n lim ρ=0.定理16.1：(柯西准则)平面点列{P n }收敛的充要条件是：任给正数ε，存在正整数N ，使得当n>N 时，对一切正整数p ，都有ρ(P n ,P n+p )<ε. 证：[必要性]设∞→n lim P n =P 0, 则由三角不等式有ρ(P n ,P n+p )≤ρ(P n ,P 0)+ρ(P n+p ,P 0)，由点列收敛定义，?ε>0，?正整数N ，当n+p>n>N 时，恒有ρ(P n ,P 0n+p ,P 0)<2ε；∴ρ(P n ,P n+p )<ε.[充分性]若ρ(P n ,P n+p )<ε，则同时有|x n+p -x n |≤ρ(P n ,P n+p ) <ε，|y n+p -y n |≤ρ(P n ,P n+p ) <ε，∴∞→n lim x n =x 0，∞→n lim y n =y 0，∴∞→n lim P n =P 0，即{P n }收敛于P 0.定理16.2：(闭域套定理)设{D n }是R 2中的闭域列，它满足：(1)D n ?D n+1, n=1,2,…；(2)d n =d(D n ), ∞→n lim d n =0，则存在唯一的点P 0∈D n , n=1,2,….证：任取点列P n ∈D n , n=1,2,….∵D n+p ?D n , ∴P n ,P n+p ∈D n , 如图有ρ(P n ,P n+p )≤d n →0, n →∞. 由定理16.1知，存在P 0∈R 2，使∞→n lim P n =P 0. 任取n ，对任何正整数p ，有P n+p ∈D n+p ?D n .令p →∞，∵D n 是闭域，从而必为闭集. ∴D n 的聚点P 0∈D n ,即P0=lim P n+p∈D n, n=1,2,…. 若有P0’∈D n, n=1,2,….n→∞由ρ(P0,P0’)≤ρ(P n,P0)+ρ(P n,P0’)≤2d n→0, n→∞. 得ρ(P0,P0’)=0，∴P0=P0’. 即P0是唯一的，得证！推论：对上述闭域套{D n}，任给ε>0，存在正整数N，当n>N 时，有D n?U(P0;ε).定理16.3：(聚点定理)设E?R2为有界无限点集，则E在R2中至少有一个聚点.证法一：∵E是平面有界无限点集，∴存在一个闭正方形D1包含它. 连接正方形对边中点，把D1分成四个小的闭正方形，则在这个四个小闭正方形中，至少有一个含有E的无限个点，记为D2，同样的将D2分成四个小的闭正方形，得到D3含有E的无限个点，如此下去得到一个闭正方形序列：D1?D2?D3?…，则闭正方形序列{D n}的边长随着n趋向于无限而趋向于0，于是由闭域套定理，存在一点M0∈D n, n=1,2,….ε，任取M0的ε邻域U(M0;ε)，当n充分大时，正方形的边长小于2即D n?U(M0;ε). 又由D n的取法知U(M0;ε)含有E的无限多个点，即M0是E的聚点.证法二：若点集E不存在任何聚点，则对任意点P∈E，∵E有界，∴存在某一正数r ，使得E?U(P;r)，且U(P;r)中只包含E的有限个点. 而E的所有点都包含于U(P;r)，即E 只包含有限个点，与E 为无限点集矛盾；∴E 在R 2中至少有一个聚点.定理16.3’：有界无限点列{P n }?R 2必存在收敛子列{kn P }.定理16.4：(有限覆盖定理)设D ?R 2为一有界闭域(集)，{△α}为一开域(集)族，它覆盖了D(即D ?αα)，则{△α}中必存在有限个开域(集)△1,△2,…,△n ，它们同样覆盖了D(即D ?i n1i ?= ). 证：设有界闭域D 含在矩形[a,b]×[c,d]之中，并假设D 不能被{△α}中有限个开域所覆盖.用直线x=2b a +，y=2d c +把矩形[a,b]×[c,d]分成四个相等的闭矩形，则至少有一个闭矩形所含的D 的部分不能被{△α}中有限个开域所覆盖. 类似的，把这个矩形(或几个的其中任一)再分成四个相等的闭矩形. 按此法继续下去，可得一闭矩形套{[a n ,b n ]×[c n ,d n ]}. 其中每一个闭矩形所含的D 的部分都不能为{△α}中有限个开域所覆盖，于是每个闭矩形[a n ,b n ]×[c n ,d n ]中都至少含有D 的一点，任取其中一点(x n ,y n ), 则(x n ,y n )∈D, 且a n <x n="" <b="" ,="" c="" <y="" <d="" (n="1,2,…)." 由闭矩形套定理可知：="" 存在一点(x="" 0,y=""0)，满足对任意自然数n="" ，都有a="" ≤x="" 0≤b="" ≤y="" 0≤d="" .="" ∵∞→n="" lim="" (b="" -a="" )="n" 2a="" -b="" ∞→="0;" ∞→n="" (d="" -c="" 2<="" p="" bdsfid="171">。

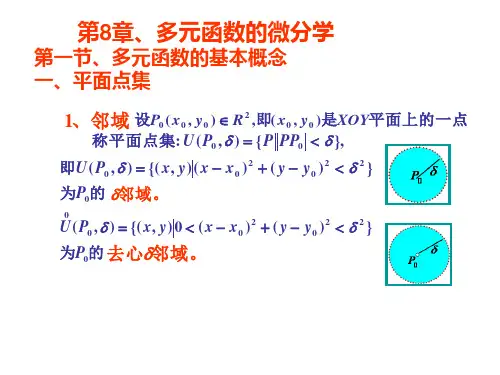
多元函数的基本概念平面点集多元函数的概念多元函数的极限多元函数的连续性平面点集建立了直角坐标系的平面称为坐标平面，记作2R =R R ⨯{}(,)|,R .x y x y =∈ 坐标平面上具有某种性质P 的点的集合，称为平面点集. 记作E (){}(,)|,.x y x y P =具有性质设000(,)P x y 是xoy 平面上的一个点， δ是某一正数，与点000(,)P x y 距离小于δ的点(,)P x y 的全体，称为 点0P 的δ邻域，记为0(,)U P δ.{}2200(,)|()().x y x x y y δ=-+-< {}0||P PP δ=<0(,)U P δ 0P δ∙（1）内点：设E 是平面上的一个点集，P 是平面上的一个点，如果存在点P 的某一个邻域()U P E ⊂， 则P 称为E 的内点.（2）外点：如果存在点P 的某一个邻域()U P E ⋂=∅，则P 称为E 的外点.EP∙EP∙ （3）边界点：如果点P 的任一邻域既含有属于E 的点，又含有不属于E 的点，则P 称为E 的边界点.E 的边界点全体称为E 的边界，记作E ∂.如果对于任意给定的0δ>，点P 的去心邻域(,)U P δ 内总含有属于E 的点，则P 称为E 的聚点.点集E 的聚点可能属于E ，也可能不属于E .（1）如果点集E的点都是E的内点，则称E为开集.（2）如果点集E的边界E E∂⊂，则称E为闭集.（3）如果点集E内任何两点，都可用折线联接起来，且该折线上的点都属于E，则称E为连通集.（4）连通的开集称为区域或开区域.∙∙重要的平面点集（5）开区域连同它的边界一起构成的点集称为闭区域.（6）如果存在某一个正数r ，使得(),E U O r ⊂，其中 O 是坐标原点，则称E 为有界集.否则，称之为无界集.例如 点集22{(,)|14}x y x y ≤+≤是有界集.Oxy点集{(,)|0}x y x y +>是无界集.Oxy多元函数的概念R的一个非空子集,如果对于D内的任一点定义设D是2x y，按照某种法则都有唯一确定的实数z与之对应，(,)则称f是D上的二元函数，记作∈z f P=，P D∈或()=，(,)x y D(,)z f x y点集D称为该函数的定义域,x和y称为自变量,z称为因变量.f x y的全体所构成的集合称为函数f的值域，数值(,)f D，即记作()z z f x y x y D=∈f D={|(,),(,)}()约定如果一个用算式表示的函数没有明确指出定义域，则x y 则该函数的定义域理解为使算式有意义的所有点(,)所成的集合,称为自然定义域.例 求二元函数222arcsin(3)(,)x y f x y x y--=-的定义域.所求定义域为222{(,)|24,}.D x y x y x y =≤+≤>22224x y x y⎧≤+≤⎨>⎩ 222310x y x y ⎧--≤⎪⎨->⎪⎩解2Oxy2设函数(,)z f x y =的定义域为D ，对于任意取定的(,)P x y D ∈，对应的函数值为(,)z f x y =，这样，以x为横坐标、y 为纵坐标、z 为竖坐标在空间就确定一点(,,)M x y z ，当(),x y 取遍D 上一切点时，得一个空间点集{(,,)|(,),(,)}x y z z f x y x y D =∈，这个点集称为二元函数(,)z f x y =的图形.二元函数的图形通常是一张曲面.类似地,可定义三元及三元以上的函数.n 时,n元函数统称为多元函数.当2多元函数的极限定义 设函数()(,)f P f x y =的定义域为D ，000(,)P x y 是D 的聚点，如果存在常数A ，对于任意给定的正数ε，|()||(,)|f P A f x y A ε-=-<成立，则称A 为函数总存在正数δ，使得当点()()0,,P x y D U P δ∈⋂时，(,)f x y 当()()00,,x y x y →时的极限， 记作()()00,,lim (,)x y x y f x y A →=，或00(,)((,)(,))f x y Ax y x y →→.也记作0lim ()P P f P A →=，或0()()f P AP P →→.我们把二元函数的极限叫做二重极限.类似地,可定义n 元函数的极限概念.例 求极限()()2222,0,01lim ()sin .x y x y x y→++ 解 令22u x y =+，则()()2222,0,01lim ()sin x y x y x y→++ 01lim sin u u u→= 0.=注意 二重极限存在是指(),P x y 以任何方式趋于000(,)P x y时，(,)f x y 都无限接近于A .确定极限不存在的常用方法：找两种不同趋近方式，使()()00,,lim (,)x y x y f x y →存在，但两者不相等，此时可断言(,)f x y 在点000(,)P x y 处极限不存在．解 例 证明()()22,0,0limx y xyx y→+不存在． 取(y kx k =为常数),则()()22,0,0limx y xy x y →+ 2220lim x y kxx kx x k x →=⋅=+ 极限的值随k 的变化而变化 , 故极限不存在.21k k=+多元函数的连续性定义 设函数()(,)f P f x y =的定义域为D ，000(,)P x y 是D 的聚点，且0P D ∈.如果()()0000,,lim(,)(,)x y x y f x y f x y →=则称函数(,)f x y 在点000(,)P x y 处的连续. 如果函数(,)f x y 在点000(,)P x y 处不连续，则称点000(,)P x y是(,)f x y 间断点.解 例 讨论二元函数(,)f x y 在(0,0)处的连续性.令cos x ρθ=，sin y ρθ=，()(),0,0lim(,)x y f x y → 33lim (sin cos )ρρθθ→=+0(0,0)f ==3322,(,)(0,0)(,)0,(,)(0,0)x yx y f x y x y x y ⎧+≠⎪=+⎨⎪=⎩注意多元连续函数经过四则运算和复合运算后仍为连续函数.由常数及具有不同自变量的一元基本初等函数经过有限次的四则运算和复合所构成的可用一个式子表示的多元函数称为多元初等函数.一切多元初等函数在其定义区域内是连续的.所谓定义区域是指包含在定义域内的区域或闭区域.解例 求()(),0,011lim.x y xy xy→+-()(),0,011limx y xy xy→+-()(),0,01lim11x y xy →=++1.2=定理1(最大值和最小值定理)在有界闭区域D上的多元连续函数，必定在D上有界，且能取得它的最大值和最小值.定理2(介值定理)在有界闭区域D上的多元连续函数，必取得介于最大值和最小值之间的任何值.定理3(一致连续性定理) 在有界闭区域D 上的多元连续函数必定在D 上一致连续.即 若()f P 在有界闭区域D 上连续，则对于任意给定的正数 ε，总存在正数δ，使得对于D 上的任意两点1P 、2P ， 只要12||P P δ<时，都有12|()()|f P f P ε-<.。