Tobit模型、泊松模型

Tobit模型估计方法与应用（一）周华林李雪松2012-10-25 10:01:28 来源：《经济学动态》(京)2012年5期第105～119页内容提要：Tobit模型从最初的结构式模型扩展到时间序列模型、面板数据模型以及非参数模型等形式，无论Tobit模型的结构形式如何变化，现有的估计方法基本上都是在Heckman(1976)两步法的基础上扩展的。

本文结合一些经典文献，介绍了不同类型的Tobit 模型的结构形式、估计方法、估计结果的性质等，为做实证分析的研究者们提供一个分析此类问题的基本方法。

关键词：Tobit模型 Heckman两步法面板Tobit模型 Tobit GARCH ARCH模型作者简介：周华林，中国社会科学院研究生院，电子邮箱：zhimadexin009@16一、引言自从Tobin(1958)研究了被解释变量有上限、下限或者存在极值等问题以来，这类研究受到学者们的广泛关注。

人们为了纪念Tobin对这类模型的贡献，把被解释变量取值有限制、存在选择行为的这类模型称之为Tobit模型。

这类模型实际上包含两种方程，一种是反映选择问题的离散数据模型；一种是受限制的连续变量模型。

第二种模型往往是文献中人们更感兴趣的部分。

Tobit模型不同于离散选择模型和一般的连续变量选择模型，它的特点在于因变量是受限变量，模型实际上由两类方程组成，主要研究在某些选择行为下，连续变量如何变化的问题。

当前，这种模型已经引入了更复杂的形式，面板数据、半参数等形式的Tobit模型在研究中广泛应用。

国外这种模型已经陆续在各领域内广泛使用，国内也有一些实证分析的论文用到了这种模型。

但是人们在应用这些模型分析问题时还存在一些误区，如误认为离散选择模型就是Tobit模型，无法解释样本选择性偏差的经济含义，不区分所建立的模型是否是联立方程，对估计结果的性质不进行检验等。

本文所介绍的经典文献，概括了Tobit模型的起源、结构形式、估计方法、适用的研究问题、自身缺陷等方面，这些经典文献中提到的一些细节问题在实证分析中很重要，然而现在已有的教材或者引文并没有摘录出来，可能导致一些作者在实证分析中对该模型有种种误解。

tobit模型公式(一)Tobit模型公式Tobit模型是一种常用的统计模型，用于处理有截断取值的数据。

在该模型中，有些观测值可能无法被观测到，只能观测到其上限或下限。

下面列举了Tobit模型的相关公式，并通过示例进行解释说明。

Tobit模型Tobit模型是由Tobin于1958年提出的，用于处理存在自我选择（指对于某些观测值可能不可观测）的取值。

在Tobit模型中，存在两个阶段的生成过程：一个线性回归方程用于预测变量取值的期望，以及一个二项分布模型来描述观测值的可能取值范围。

Tobit模型公式Tobit模型可以表示为以下公式：1.观测方程： [观测方程]( [观测方程](其中，[观测方程](2.似然函数： [似然函数](其中，[似然函数](3.最大似然估计：最大似然估计的目标是最大化似然函数，从而找到最优的回归系数和误差项方差。

示例解释假设我们想研究商品房的售价与面积之间的关系，但房价数据存在下限（价格为0），无法观测到低于该下限的房价。

我们可以使用Tobit模型来估计房价与面积之间的线性关系。

首先，我们根据样本数据拟合Tobit模型，得到回归系数和误差项方差的最大似然估计。

然后，我们可以根据估计的回归系数，计算面积对房价的影响。

最后，我们可以使用模型进行预测，根据不同的面积值估计对应的房价。

通过Tobit模型，我们可以得出结论，面积与房价呈正相关关系，面积越大，房价越高。

这可以帮助我们了解房价的形成机制，并为房地产市场的决策提供参考。

总结Tobit模型是一种用于处理有截断取值的数据的统计模型。

通过估计回归系数和误差项方差，Tobit模型可以帮助我们理解变量之间的关系，并进行预测。

在实际应用中，Tobit模型在经济学、金融学等领域被广泛使用。

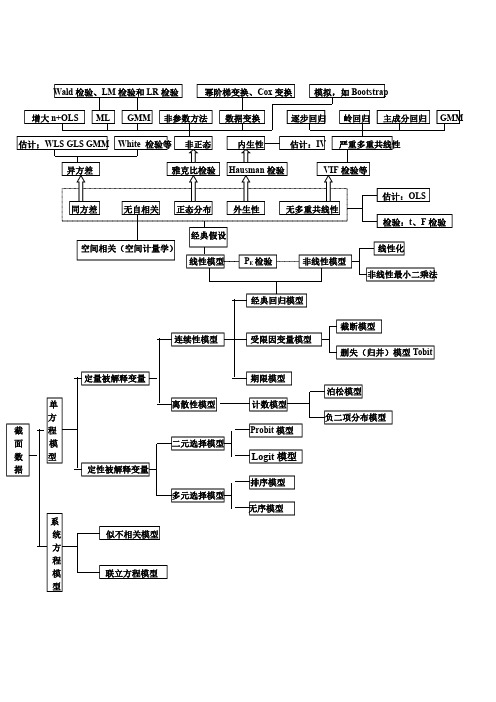
二元选择摸型如果回归模型的解释变量中含有定性变量，则可以用虚拟变量处理之。

在实际经济问题中，被解释变量也可能是定性变量。

如通过一系列解释变量的观测值观察人们对某项动议的态度，某件事情的成功和失败等。

当被解释变量为定性变量时怎样建立模型呢？这就是要介绍的二元选择模型或多元选择模型，统称离散选择模型。

这里主要介绍Tobit （线性概率）模型，Probit （概率单位）模型和Logit 模型。

1．Tobit （线性概率）模型 Tobit 模型的形式如下，y i = α + β x i + u i (1) 其中u i 为随机误差项，x i 为定量解释变量。

y i 为二元选择变量。

此模型由James Tobin 1958年提出，因此得名。

如利息税、机动车的费改税问题等。

设 1 （若是第一种选择） y i =0 （若是第二种选择）-0.20.00.20.40.60.81.01.2330340350360370380XY对y i 取期望，E(y i ) = α + β x i (2) 下面研究y i 的分布。

因为y i 只能取两个值，0和1，所以y i 服从两点分布。

把y i 的分布记为， P ( y i = 1) = p i P ( y i = 0) = 1 - p i 则E(y i ) = 1 (p i ) + 0 (1 - p i ) = p i (3) 由（2）和（3）式有p i = α + β x i （y i 的样本值是0或1，而预测值是概率。

） (4)以p i = - 0.2 + 0.05 x i 为例，说明x i 每增加一个单位，则采用第一种选择的概率增加0.05。

现在分析Tobit 模型误差的分布。

由Tobit 模型（1）有，u i = y i - α - β x i =⎩⎨⎧=--=--0,1,1i i i i y x y x βαβαE(u i ) = (1- α - β x i ) p i + (- α - β x i ) (1 - p i ) = p i - α - β x i 由（4）式，有E(u i ) = p i - α - β x i = 0因为y i 只能取0, 1两个值，所以，E(u i 2) = (1- α - β x i )2 p i + (- α - β x i )2 (1 - p i )= (1- α - β x i )2 (α + β x i ) + (α +β x i )2 (1 - α - β x i ), （依据(4)式） = (1- α - β x i ) (α + β x i ) = p i (1 - p i ) , （依据(4)式） = E(y i ) [1- E(y i ) ]上两式说明，误差项的期望为零，方差具有异方差。

Tobit模型估计方法与应用一、本文概述本文旨在全面探讨Tobit模型估计方法及其应用。

Tobit模型，也称为截取回归模型或受限因变量模型，是一种广泛应用于经济学、社会学、生物医学等领域的统计模型。

该模型主要处理因变量在某一范围内被截取或受限的情况，例如，当因变量只能取正值或只能在某一特定区间内变动时。

本文首先将对Tobit模型的基本理论进行阐述，包括模型的设定、参数的估计方法以及模型的检验等方面。

随后，文章将详细介绍Tobit模型在各个领域中的应用案例，包括工资水平、耐用消费品需求、医疗支出等方面的研究。

通过这些案例，我们将展示Tobit模型在处理受限因变量问题时的独特优势和应用价值。

文章还将对Tobit模型的发展趋势和前景进行展望，以期为相关领域的研究提供有益的参考和启示。

二、Tobit模型的基本原理Tobit模型，也称为受限因变量模型或截取回归模型，是一种广泛应用于经济学、社会学、生物医学等领域的统计模型。

该模型主要处理因变量受到某种限制或截取的情况，例如因变量只能取正值、只能在某个区间内取值等。

Tobit模型的基本原理基于最大似然估计法，通过构建似然函数来估计模型的参数。

截取机制：在Tobit模型中，因变量的取值受到某种截取机制的限制。

这种截取机制可以是左截取、右截取或双侧截取。

左截取意味着因变量只能取大于某个阈值的值，右截取则意味着因变量只能取小于某个阈值的值，而双侧截取则限制了因变量的取值范围在两个阈值之间。

潜在变量：在Tobit模型中，通常假设存在一个潜在变量（latent variable），它是没有受到截取限制的因变量。

潜在变量与观察到的因变量之间的关系由截取机制决定。

潜在变量通常假设服从某种分布，如正态分布。

最大似然估计：在给定截取机制和潜在变量分布的假设下，可以通过构建似然函数来估计Tobit模型的参数。

似然函数反映了观察到的数据与模型参数之间的匹配程度。

通过最大化似然函数，可以得到模型参数的估计值。

泊松扩散模型基本思路泊松扩散模型是一种常用的数学模型，用于描述随机过程中的粒子扩散行为。

它由法国数学家西蒙·泊松于19世纪中叶提出，被广泛应用于物理、化学、生物、金融等领域的研究中。

本文将从泊松扩散模型的基本思路入手，介绍该模型的原理和应用。

泊松扩散模型的基本思路是将扩散的粒子视为泊松过程，即粒子在时间和空间上的分布服从泊松分布。

泊松分布是一种概率分布，描述了在一个固定时间或空间区间内，事件发生的次数的概率。

在泊松扩散模型中，将粒子的扩散视为一系列独立的随机事件，每个事件表示粒子从一个位置跳到另一个位置的概率。

这些跳跃事件之间的时间间隔服从指数分布，描述了粒子在不同位置之间扩散的速率。

泊松扩散模型的数学表达是通过偏微分方程来描述的。

该方程称为扩散方程，形式上是一个二阶偏导数方程，描述了粒子浓度随时间和空间变化的规律。

扩散方程的解可以通过数值方法或解析方法求得，从而得到粒子的扩散行为。

泊松扩散模型的应用十分广泛。

在物理学中，它被用于描述热传导、电子扩散等过程。

在化学反应动力学中，泊松扩散模型可以用于描述反应物在溶液中的扩散行为。

在生物学中，它被应用于描述细胞内物质的扩散和传输。

在金融学中，泊松扩散模型可以用于描述股票价格的随机波动。

泊松扩散模型的优点是简单易用，适用于描述一些简单的扩散过程。

它可以通过调整模型参数来适应实际情况，从而得到更准确的结果。

然而，泊松扩散模型也有一些局限性。

它假设粒子之间的相互作用是弱的，忽略了粒子之间的相互作用对扩散行为的影响。

对于复杂的扩散过程，泊松扩散模型可能无法给出准确的结果。

泊松扩散模型是一种常用的数学模型，可以描述随机过程中的粒子扩散行为。

它的基本思路是将扩散的粒子视为泊松过程，通过偏微分方程来描述粒子的扩散行为。

泊松扩散模型具有简单易用、适应性强的优点，被广泛应用于物理、化学、生物、金融等领域的研究中。

然而，它也存在一些局限性，对于复杂的扩散过程可能无法给出准确的结果。