计算机中的讲义数制表示

七年级上册信息技术第2课计算机中的数制说课稿尊敬的各位专家、评委你们好！我是号考生，今天我要和大家分享的说课题目是《计算机中的数制》，在说课的过程中希望得到专家的批评和指导：一、说教材：通过本课的学习，不仅要让学生知道什么是二进制，而且要让学生能对二进制进行简单的运算，为学生以后的信息技术的学习打下坚实的基础！二、说学生:我们的学生大多家中有电脑，他们也大都接触过电脑，所以他们对电脑并不陌生。

再加上本节课内容比较简单，所以他们学习起本课来应当比较容易。

三、说教学目标根据学生的基本情况和教材的基本要求我确定本课的目标为：知识目标：知道什么是二进制；技能目标：能对二进制进行简单的运算；情感目标：培养学生对电脑的兴趣；四、说重难点：根据教学目标和学生的情况我确定本课的重难点为：教学重点：了解计算机的常用数制；教学难点：会对计算机常用数制进行转换；五、说教学准备：老师准备：多媒体课件；六、教学过程：一、激趣导入：师：同学们你们知道计算机的常用数制有哪些？它们是如何进行转换的？师：下面就让我们一起学习今天的内容（板书）《计算机中的数值》。

二、认识数制：师：课件出示课本几幅关于计算机的图片，请同学们认真观看后，结合课文内容想一想，什么是数制？生活中都有哪些数制？生：仔细观察后，结合课文积极分组讨论；师：巡视指导；生：积极举手回答；师：大家说的很好，看来同学们已经基本了解了数制；三、数制之间的相互转换：师：刚才我们了解了数制，现在请同学们结合课文内容想一想，不同数制之间是怎样相互转换的？生：结合课文积极进行讨论；师：巡视指导；师：大家说的都很好，说明大家已经学会了数制之间的相互转换！师：下课同学们再见！以上是我在预设教学《计算机中的数制》一课时一些不成熟的想法,敬请各位评委老师点评,指导。

谢谢大家！。

计算机中的数制与数制转换一、引言计算机中的数制是指用来表示和处理数字的方式，常见的数制包括二进制、八进制、十进制和十六进制。

数制转换是指在不同数制之间进行转换，其中二进制和十六进制在计算机中应用较为广泛。

本文将详细介绍计算机中的数制及其转换方法。

二、二进制1. 二进制概述二进制是计算机中最基本的数制，由0和1组成。

计算机内部的所有数据都以二进制形式存储和处理。

二进制数的每一位称为一个比特（bit），8个比特组成一个字节（byte）。

2. 二进制转换为十进制二进制数转换为十进制数的方法是将每个位上的数与对应的权相乘，然后求和。

例如，二进制数1101转换为十进制数的计算过程为：1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 133. 二进制转换为八进制和十六进制二进制数转换为八进制数和十六进制数的方法是先将二进制数按照每3位或4位分组，然后将每组转换为对应的八进制数或十六进制数。

例如，二进制数101101转换为八进制数和十六进制数的过程为：（1）将二进制数按照每3位分组，得到001和011，分别对应于八进制数1和3，因此八进制数为13；（2）将二进制数按照每4位分组，得到0010和1101，分别对应于十六进制数2和D，因此十六进制数为2D。

三、八进制1. 八进制概述八进制是一种基数为8的数制，由0、1、2、3、4、5、6、7组成。

在计算机中，八进制数常用于表示文件权限等信息。

2. 八进制转换为二进制和十六进制八进制数转换为二进制数和十六进制数的方法是将每个八进制位转换为对应的3位二进制数或1位十六进制数。

例如，八进制数17转换为二进制数和十六进制数的过程为：（1）将八进制数按照每位转换为对应的3位二进制数，得到001和111，因此二进制数为111；（2）将八进制数按照每位转换为对应的1位十六进制数，得到F，因此十六进制数为F。

四、十进制1. 十进制概述十进制是人类常用的数制，由0、1、2、3、4、5、6、7、8、9组成。

计算机中数制的基本概念数制的三个基本概念数制：记数的方法，指用一组固定的符号和统一的规则来表示数值的方法，如在计数的过程中采用进位的方法则称为进位计数制。

进位计数制有数位、基数、位权3个要素。

数位:指数字符号在一个数中所处的位置。

基数：指在某种进位计数制中数位上所能使用的数字符号的个数，例如，十进制数的基数是10，八进制的基数是8,二进制的基数是2。

不同的数制，可以给数字加上括号，使用下标来表示该数字的数制（当没有下标时默认为十进制）。

C/C++中整数有三种表示形式：1）十进制形式。

如99、-1。

2）八进制形式。

以数字0打头，由0-7构成，如012表示八进制整数12，即12(8)。

3）十六进制形式。

以0x打头，如0x12A，表示十六进制整数12A，即12A(16)。

在数制中，还有一个规则，这就是，N进制必须是逢N进一。

计算机中常用的数制是十进制。

二进制与十进制类似，但是其基数是2，只有两个数字0和1，每超过2时就需要进位。

十进制数的特点是逢十进一。

如下图所示：2.二进制数的特点是逢二进一。

如下图所示：3.八进制数的特点是逢八进一。

如下图所示：4. 十六进制数的特点是逢十六进一。

如下图所示：二进制与十进制之间的转换•十进制转二进制方法为：十进制数除2取余法，即十进制数除2，余数为权位上的数，得到的商值继续除2，依此步骤继续向下运算直到商为0为止。

（具体用法如下图）二进制转十进制方法为：把二进制数按权展开、相加即得十进制数。

具体用法如下图：二进制与十六进制之间的转换二进制转十六进制方法为：与二进制转八进制方法近似，八进制是取三合一，十六进制是取四合一。

（注意事项，4位二进制转成十六进制是从右到左开始转换，不足时补0）。

具体用法如下图：十六进制转二进制方法为：十六进制数通过除2取余法，得到二进制数，对每个十六进制为4个二进制，不足时在最左边补零。

具体用法如下图：。

计算机基础知识之数制与编码数制是计算机基础知识中非常重要的一部分，它涉及到了计算机中数字的表示和存储方式。

编码则是将数字和字符等信息转换成计算机能够识别和处理的形式。

在计算机领域中，常用的数制有二进制、十进制、十六进制等，而编码方式常见的有ASCII、Unicode、UTF-8等。

接下来，我们将详细介绍数制与编码的概念、特性以及在计算机中的运用。

一、数制1.二进制二进制是计算机中最基本的数制。

它使用了 0 和 1 两个数字，表示任何一个二进制位(bit)的状态。

二进制的每一位表示2的幂，从右到左依次是1、2、4、8、16、32...二进制数的转换和计算相对复杂，因此在计算机中常用于存储和处理数据。

2.十进制十进制是人类最常用的数制。

它使用了0-9十个数字，每一位表示10的幂。

十进制数的转换和计算相对简单，因此在日常生活和大多数计算中都使用十进制。

3.十六进制十六进制是二进制的一种表示方式，它使用了0-9和A-F十六个数字，每一位表示16的幂。

十六进制数比较紧凑且易于理解，因此在计算机领域中经常用于表示二进制值，尤其是内存地址和寄存器的值。

4.八进制八进制使用了0-7八个数字，每一位表示8的幂。

八进制在计算机领域中应用较少，通常仅用于一些特定的场景。

5.其他进制除了二进制、十进制、十六进制和八进制外，还有其他一些进制，如二十四进制、三十六进制等。

但它们在计算机领域中使用相对较少。

二、编码编码是将数字、字符和其他信息转换成计算机能够理解和处理的形式。

常见的编码方式有ASCII、Unicode、UTF-8等。

1.ASCII码ASCII (American Standard Code for Information Interchange)是计算机中最早使用的编码方式，它共定义了128个字符，包括数字、字母、符号和控制字符等。

每个字符用一个字节(8位）来表示，其中的 7位用于字符的编码，最高位用于保持数据的完整性。

计算机常用数制及其特点计算机常用的数制有二进制、八进制、十进制和十六进制。

每种数制都有自己的特点和应用场景。

一、二进制（Binary）二进制是计算机中最基本的数制，也是计算机内部数值表示的方式。

二进制只使用两个数字0和1来表示数值，是一种离散的数制。

在二进制中，每一位被称为一个"bit"（比特），它是计算机中最小的存储单位。

二进制的特点：1. 简单易懂：只有两个数字0和1，容易理解和使用。

2. 易于计算：二进制的计算规则与十进制相似，只需要掌握简单的加法和乘法规则即可。

3. 适合电子电路实现：计算机内部的逻辑电路使用二进制信号进行控制和传输，二进制数制可以直接反映电路的状态。

二、八进制（Octal）八进制使用8个数字（0-7）来表示数值，每一位相当于二进制的3位。

八进制一般用于计算机领域的权限管理、文件访问等场景，以及在Unix/Linux系统中的文件权限设置。

八进制的特点：1. 简洁表示：用较少的数字表示相同的数值，比二进制和十六进制更节省空间。

2. 易于转换：八进制数可以直接转换为二进制数，每一位转换为对应的三位二进制数即可。

3. 权限管理：八进制数可用于表示文件的读、写、执行权限，通过三位八进制数可以表示8种权限组合。

三、十进制（Decimal）十进制是我们最常用的数制，使用10个数字（0-9）来表示数值。

十进制数制适用于日常生活中的数值表示和计算，以及大部分编程语言中的数值表示方式。

十进制的特点：1. 直观易懂：十进制是人们最熟悉的数制，可以直接表示日常生活中的数值。

2. 便于计算：十进制的计算规则较为简单，适合进行常规的算术运算。

3. 适用广泛：大部分编程语言和软件都使用十进制来表示数值，具有较好的兼容性。

四、十六进制（Hexadecimal）十六进制使用16个数字（0-9以及A-F）来表示数值，每一位相当于二进制的4位。

十六进制广泛应用于计算机领域，特别是在底层编程、存储器地址和网络通信等方面。

数制的表示方法一、二进制表示方法二进制是一种以2为基数的数制，只包含两个数字0和1。

在计算机科学和信息技术领域，二进制表示方法被广泛使用。

在二进制表示方法中，每一位的权重是2的幂次方。

比如，二进制数1101表示的是1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 13。

在计算机系统中，所有的数据和指令都是以二进制形式存储和处理的。

计算机中的逻辑电路和逻辑门也是基于二进制的，通过开关电路的开和关来表示0和1。

因此，二进制表示方法是计算机科学的基础。

二、八进制表示方法八进制是一种以8为基数的数制，使用8个数字0-7来表示。

八进制是在二进制表示方法的基础上发展起来的，每一位的权重是8的幂次方。

比如，八进制数37表示的是3 * 8^1 + 7 * 8^0 = 31。

八进制表示方法在计算机科学中的应用相对较少，但在某些领域仍然有一定的作用。

比如，在UNIX操作系统中，文件和目录的权限通常使用八进制表示，分别代表所有者、组和其他用户的读、写和执行权限。

三、十进制表示方法十进制是一种以10为基数的数制，使用10个数字0-9来表示。

十进制表示方法是人类日常生活中最常用的表示方法。

在十进制表示方法中，每一位的权重是10的幂次方。

比如，十进制数256表示的是2 * 10^2 + 5 * 10^1 + 6 * 10^0 = 256。

十进制表示方法在数学和商业领域得到广泛应用。

人们使用十进制进行数学运算、计算货币、计算时间等。

在计算机科学中，十进制表示方法通常用于人机交互，方便人们理解和输入数据。

四、十六进制表示方法十六进制是一种以16为基数的数制，使用16个数字0-9和字母A-F来表示。

十六进制表示方法是在二进制表示方法的基础上发展起来的，每一位的权重是16的幂次方。

比如，十六进制数3F表示的是3 * 16^1 + 15 * 16^0 = 63。

十六进制表示方法在计算机科学和信息技术领域被广泛使用。

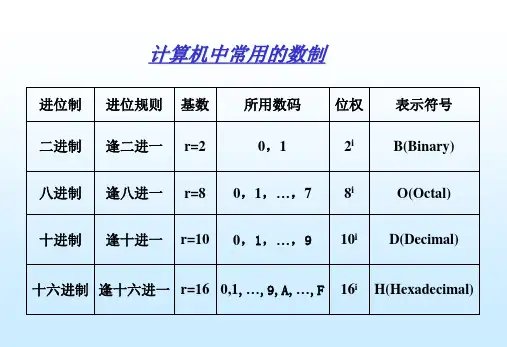
第一讲计算机中的数制及其转换计算机中常用的数制有二进制（Binary）、十进制（Decimal）、八进制（Octal）和十六进制（Hexadecimal）等。

在计算机内部，所有的数据都是以二进制方式表示和处理的。

因此，了解不同数制之间的转换对于理解计算机运行原理和进行数据处理至关重要。

1.二进制数制二进制数制只包含两个数字：0和1、在计算机中，一个二进制位（bit）是最小的数据单位，可以表示这两个数字中的任意一个。

因此，一个8位二进制数就能表示256种不同的状态（2^8=256）。

2.十进制数制十进制数制是我们平常生活中最常用的数制，包含10个数字：0-9、每一位上的数字代表相应的权值，从右往左依次为个位、十位、百位等。

例如，数字1234可以表示为1*10^3+2*10^2+3*10^1+4*10^0。

3.八进制数制八进制数制包含8个数字：0-7、每一位上的数字代表相应的权值，从右往左依次为个位、八位、六十四位等。

与十进制类似，例如数字3462可以表示为3*8^3+4*8^2+6*8^1+2*8^0。

4.十六进制数制十六进制数制包含16个数字：0-9以及A-F（分别表示十进制的10-15）。

每一位上的数字代表相应的权值，从右往左依次为个位、十六位、二百五十六位等。

与十进制类似，例如数字A3F可以表示为10*16^2+3*16^1+15*16^0。

在计算机中，不同数制之间的转换非常常见。

以下是各种数制之间的转换方法：二进制到十进制转换：按权展开法，将二进制数的每一位与对应的权值相乘再求和即可得到该二进制数对应的十进制数。

十进制到二进制转换：除以2取余数，将余数从底向上排列，就得到该十进制数对应的二进制数。

二进制到八进制转换：从右向左每三位分组，将每组二进制数转换为对应的八进制数。

八进制到二进制转换：将每一位的八进制数转换为对应的三位二进制数。

二进制到十六进制转换：从右向左每四位分组，将每组二进制数转换为对应的十六进制数。

计算机中的数制及其编码1.数制的定义：数制是用来表示和运算数字的一种符号系统。

常见的数制包括二进制、八进制、十进制和十六进制。

2.二进制：二进制是数字系统的一种数制，只包含两个数字0和1、在计算机中，所有的信息都被转换为二进制形式进行存储和处理。

3.八进制：八进制是一种数制，基数为8、它使用了8个数字0-7，通过每一位上的数来表示数值。

4.十进制：十进制是我们日常生活中最常用的数制，基数为10。

它使用了10个数字0-9来表示数值。

5.十六进制：十六进制也是一种常见的数制，基数为16、它使用了16个数字0-9和字母A-F来表示数值。

十六进制常用于计算机科学和工程领域，特别是在内存地址和颜色编码中。

6.数制之间的转换：在计算机中，不同的数制之间可以进行相互转换。

例如，将十进制数转换为二进制数可以使用除2取余的方法，将十进制数一直除以2，直到商为0，然后将每次的余数倒序排列即可得到二进制数。

而将二进制数转换为十进制数，则可以通过每一位数乘以2的幂次方后相加得到结果。

7.数制的编码：在计算机中，数制的编码主要指对不同的字符和数字进行表示和存储的方式。

常见的编码方式包括ASCII码、Unicode、UTF-8等。

-ASCII码：ASCII码是一种基于拉丁字母的字符编码标准，使用7位或8位二进制（0-127或0-255）表示128个不同的字符。

它包括英文字母、数字、标点符号和控制字符等。

- Unicode：-UTF-8：UTF-8是一种可变长度的Unicode编码，使用8位二进制（0-255）表示字符。

它通过对不同的字符使用不同长度的编码，实现了用较少的存储空间表示更多的字符。

总结：数制是用来表示和运算数字的一种符号系统，常见的数制包括二进制、八进制、十进制和十六进制。

数制之间可以进行相互转换，常见的编码方式包括ASCII码、Unicode和UTF-8、这些数制和编码在计算机中起着重要的作用，帮助实现了数字的存储、处理和通信。

全国计算机一级考试MSOffice考点：数制2015全国计算机一级考试MSOffice考点：数制1.十进制计欺制其加法规则是“逢十进一”，任意一个十进制数值都可用0. 1.2 .3 .4 .5 .6 .7 .8 .9共10个数字符号组成的字符串来表示，这些数字符号称为数码;数码处于不同的位置代表不的数值。

例如720.30可以写成7x102+2x101+0x100+3 x10 1+0x10 2，此式称为按权展开表示式2. R进制计数制从十进制计数制的分析得出，任意R进制计数制同样有基数N、和Ri按权展开的表示式。

R可以是任意正整数如二进制R为2。

(1)基数(Radix)一个计数所包含的数字符号的个数称为该数的基，.用R表示。

例如，对二进制来说，任意一个二进制数可以用0，1两个数字符表示，其基数R等于2。

(2)位值(权)任何一个R进制数都是由一串数码表示的，其中每一位数码所表示的实际值都大小，除数码本身的数值外，还与它所处的位置有关，由位置决定的值就称为位置(或位权)。

位置用基数R的I次幂Ri表示。

假设一个R进制数具有n为整数，m位小数，那么其位权为Ri，其中i=-m~n-1。

(3)数值的.按权展开任一R进制数的数值都可以表示为：各个数码本身的值与其权的乘积之和。

例如，二进制数101.01的按权展开为：101.01B=1×22+0×21+1×20+0×2-1+1×2-2=5.25D任意一个具有n位整数和m位小数的R进制数的按权展开为：(N)R=dn-1×RN-1+dn-2×RN-2+…+d2×R2+d1×R1+d0×R0+d-1×R-1+…+d-M×R-M其中di为R进制的数码。