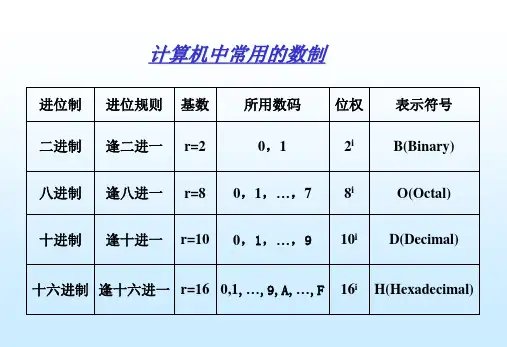
计算机中常用的数制
- 格式:ppt
- 大小:914.00 KB
- 文档页数:36

一、常用数制及其相互转换在我们的日常生活中计数采用了多种记数制,比如:十进制,六十进制(六十秒为一分,六十分为一小时,即基数为60,运算规则是逢六十进一),……。
在计算机中常用到十进制数、二进制数、八进制数、十六进制数等,下面就这几种在计算机中常用的数制来介绍一下。
1.十进制数我们平时数数采用的是十进制数,这种数据是由十个不同的数字0、1、2、3、4、5、6、7、8、9任意组合构成,其特点是逢十进一。
任何一个十进制数均可拆分成由各位数字与其对应的权的乘积的总和。
例如:???这里的10为基数,各位数对应的权是以10为基数的整数次幂。
为了和其它的数制区别开来,我们在十进制数的外面加括号,且在其右下方加注10。
2.二进制数在计算机中,由于其物理特性(只有两种状态:有电、无电)的原因,所以在计算机的物理设备中获取、存储、传递、加工信息时只能采用二进制数。
二进制数是由两个数字0、1任意组合构成的,其特点是逢二进一。
例如:1001,这里不读一千零一,而是读作:一零零一或幺零零幺。
为了与其它的数制的数区别开来,我们在二进制数的外面加括号,且在其右下方加注2,或者在其后标B。
任何一个二进制数亦可拆分成由各位数字与其对应的权的乘积的总和。
其整数部分的权由低向高依次是:1、2、4、8、16、32、64、128、……,其小数部分的权由高向低依次是:0.5、0.25、0.125、0.0625、……。
二进制数也有其运算规则:加法:0+0=0????0+1=1???1+0=1????1+1=10乘法:0×0=0????0×1=0????1×0=0????1×1=1二进制数与十进制数如何转换:(1)二进制数—→十进制数对于较小的二进制数:对于较大的二进制数:方法1:各位上的数乘权求和??例如:(101101)2=1×25+0×24+1×23+1×22+0×21+1×20=45(1100.1101)2=1×23+1×22+0×21+0×20+1×2-1+1×2-2+0×2-3+1×2-4=12.8125方法2:任何一个二进制数可转化成若干个100…0?的数相加的总和??例如:(101101)2=(100000)2+(1000)2+(100)2+(1)2而这种100…00形式的二进制数与十进制数有如下关联:1后有n个0,则这个二进数所对应的十进制数为2n。



数制
数制——数的制式。
是人们利用符号计数的一种方法。
数制有很多种,常用的有十进制、二进制、十六进制。
1)十进制(Decimal)
数码:0 1 2 3 4 5 6 7 8 9十个
基数:10
计数规则:逢十进一
日常生活中人们习惯于十进制计数制,但是对于计算机硬件电路,只有通/断或电平的高/低两种状态,为便于对数字信号的识别与计算,计算机采用二进制。
2)二进制(Binary)
数码:0 1
基数:2
计数规则:逢二进一
8位二进制数称为一个字节,Byte(8位)。
2个字节称为一个字,Word(16位)。
2个字称为一个双字,Double Word(32位)。
210= 1024称为1K。
二进制数较大时,书写和阅读均不方便,通常将四位二进制数合为一位,用十六进制数表示。
3)十六进制(Hexadecimal)
数码:0 1 2 3 4 5 6 7 8 9 A B C D E F十六个
基数:16
计数规则:逢十六进一
如二进制数1010 0101B可表示为A5H,其值为十进制的165(=10×161+5×160)。
编码
1)BCD码
有些场合,计算机输入/输出数据时仍使用十进制数,以适应人们的习惯。
为此,十进制数必须用二进制码表示,这就形成了二进制编码的十进制数,称为BCD码(Binary Coded Decimal)。
BCD码是用四位二进制数表示一位十进制数,它们之间的对应关系如下表所示。

几个重要概念重点概念1:计算机中的数据都是以二进制形式进行存储和运算的重点概念2:在计算机中存储数据时,每类数据占据固定长度的二进制数位,而不管其实际长度。
一般长度为字节的整倍数例如:在八位微机中,整数216 存储为11011000B整数56 存储为00111000B复习1)十进制特点:每一位数有02)二进制特点:3)十六进制特点:1(即乘10101000376542复习真值与机器数例:真值与机器数+77机机例:真值与机器数-77机机2数的定点与浮点表示计算机中如何表示实数中的小数点呢?计算机中不用专门的器件表示小数点,而是用数的两种不同的表示法来表示小数点的位置。
根据小数点的位置是否固定,数的表示方法分为定点表示和浮点表示,相应的机器数称为定点数和浮点数。
任意一个二进制数N均可表示为:N=S·2J其中:最后面或最前面,即分为定点纯小数与定点纯整数两类,如图1-6所示。
01000000定点小数:定取不同的数值,则在计算机中除了要表示尾码示阶码J。
因此,一个浮点数表示为阶码和尾数两部分,尾数一般是定点纯小数,阶码是定点纯整数,其形式如图点N = 2p S点例:X= +10110.01= 2 +101×(+ 0.1011001)26点= 2无符号数带符号数数有正、负→带符号数把符号位和数值位一起编码:原码,反码,补码。
顺时针调:7+9 =4 (mod 12)逆时针调:7-3 =4 (mod 12)由于时钟上超过12点时就会自动丢失一个数与原码相同,只要将符号位的得到它的真值。
对一个二进制数按位取反,最低位加1。
(计算机 已知负数的补码求真值在计算机中,用补码表示方法:按位取反,最低位加12 105 2 52 12 26 0[ 105D ] 补8位= 0 –0110 1001B = 0 –69H -D 2000:0 如,用DEBUG 查看到存放在内存中的一组符号数:由最高位判断:0 →正数7DH的真值= 7 ×16 + 13 = 125 D凡是能在计算机内存储或参与运算的都是二进制形式的机器数,计算机只能出别“0”和“1”,对于某个二进别致的最高位究竟应看做为符号位还是数值位,理论上是无法自动识别但是,由于引入了补码概念,使得计算机在进行无符号数和有符号数的运算时能够实现操作的一致性,且结果合理。

转~~````数制是人们利用符号进行计数的科学方法。
数制有很多种,在计算机中常用的数制有:十进制,二进制和十六进制。
1.十进制数人们通常使用的是十进制。
它的特点有两个:有0,1,2….9十个基本字符组成,十进制数运算是按“逢十进一”的规则进行的.在计算机中,除了十进制数外,经常使用的数制还有二进制数和十六进制数.在运算中它们分别遵循的是逢二进一和逢十六进一的法则.2.二进制数3.二进制数有两个特点:它由两个基本字符0,1组成,二进制数运算规律是逢二进一。
为区别于其它进制数,二进制数的书写通常在数的右下方注上基数2,或加后面加B表示。
例如:二进制数10110011可以写成(10110011)2,或写成10110011B,对于十进制数可以不加注.计算机中的数据均采用二进制数表示,这是因为二进制数具有以下特点:1)二进制数中只有两个字符0和1,表示具有两个不同稳定状态的元器件。
例如,电路中有,无电流,有电流用1表示,无电流用0表示。
类似的还比如电路中电压的高,低,晶体管的导通和截止等。
2)二进制数运算简单,大大简化了计算中运算部件的结构。
二进制数的加法和乘法运算如下:0+0=0 0+1=1+0=1 1+1=100×0=0 0×1=1×0=0 1×1=1由于二进制数在使用中位数太长,不容易记忆,所以又提出了十六进制数.3.十六进制数十六进制数有两个基本特点:它由十六个字符0~9以及A,B,C,D,E,F组成(它们分剖别表示十进制数0~15),十六进制数运算规律是逢十六进一, 鹩谄渌 剖 氖樾赐ǔT谑 挠蚁路阶⑸匣 保叮 蚣雍竺婕樱缺硎尽?/SPAN>例如:十六进制数4AC8可写成(4AC8)16,或写成4AC8H。
4.数的位权概念5.一个十进制数110,其中百位上的1表示1个102,既100,十位的1表示1个101,即10,个位的0表示0个100,即0。
一个二进制数110,其中高位的1表示1个22,即4,低位的1表示1个21,即2,最低位的0表示0个20,即0。

数制与进制
数制是人类为了方便计数而发明的一种记数系统,它是由一组不同的符号来表示不同的数值。
常见的数制有十进制、二进制、八进制和十六进制等。
十进制是我们日常生活中最为常见的数制,它是基于十个数字
0~9来进行计数的。
而二进制则是计算机中最常用的数制,它仅使用两个数字0和1来进行表示。
八进制和十六进制也常常出现在计算机科学中,它们分别使用八个和十六个不同的数字来进行计数。
在进行数制转换时,需要了解各个数制之间的进制关系。
例如,十进制数转换为二进制数时,可以通过不断地将十进制数除以2并取余数的方式来得到相应的二进制数。
同样地,二进制数转换为十进制数时,可以通过将每位上的数字与相应的权值相乘并相加来得到十进制数。
不同的数制在计算机科学中具有不同的应用场景。
二进制数被广泛应用于数字电路设计和计算机内部数据传输等领域,而八进制和十六进制则是为了方便人们对大型二进制数进行表示和阅读而发明的。
了解数制和进制关系可以帮助我们更好地理解和应用计算机科学中
的一些基本概念和算法。
- 1 -。

计算机中的数制和码制教案一、教学目标1. 让学生了解计算机中常用的数制,如二进制、十进制、十六进制等。
2. 使学生掌握不同数制之间的转换方法。
3. 让学生了解计算机中的编码方式,如ASCII码、Uni码等。
4. 培养学生运用数制和码制解决实际问题的能力。
二、教学内容1. 数制的概念及表示方法数制的定义:数制是一种表示数值的方法,计算机中常用的数制有二进制、十进制、十六进制等。
不同数制的表示方法及转换关系。
2. 二进制与十进制的转换二进制与十进制之间的转换方法。
练习题:进行二进制与十进制的相互转换。
3. 十六进制与十进制的转换十六进制与十进制之间的转换方法。
练习题:进行十六进制与十进制的相互转换。
4. 计算机中的编码方式ASCII码:字符与二进制之间的对应关系。
Uni码:字符集的扩展与多语言支持。
练习题:根据字符写出对应的ASCII码或Uni码。
三、教学方法1. 讲授法:讲解数制的概念、转换方法及编码方式。
2. 实践法:让学生通过练习题进行实际操作,巩固所学知识。
3. 讨论法:分组讨论实际问题,培养学生解决问题的能力。
四、教学步骤1. 引入数制的概念,讲解不同数制的表示方法及转换关系。
2. 讲解二进制与十进制的转换方法,进行练习。
3. 讲解十六进制与十进制的转换方法,进行练习。
4. 介绍计算机中的编码方式,讲解ASCII码和Uni码的概念及应用。
5. 根据字符写出对应的ASCII码或Uni码,进行练习。
五、教学评价1. 课堂问答:检查学生对数制和码制的理解程度。
2. 练习题:评估学生运用数制和码制解决问题的能力。
3. 小组讨论:评价学生在团队合作中解决问题的能力。
六、教学内容6. 数制转换的实际应用讲解在计算机系统中如何使用不同数制进行数据表示和处理。
分析实际案例,展示不同数制转换在计算机科学中的应用。
练习题:解决实际问题,如计算机存储、数据传输中的数制转换。
7. 计算机中的高级编码技术介绍计算机中除ASCII码和Uni码外的其他编码方式,如UTF-8、UTF-16等。

计算机中常用的数制一、几种常用的进位计数制1.十进制 (10个基本数码:0、1、2、3、4、5、6、7、8、9)2.二进制(2个基本数码:0、1)3.八进制(8个基本数码:0、1、2、3、4、5、6、7)4.十六进制(16个基本数码:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F)二、计算机常用的各种进制数的特点三、不同进位计数制间数据的转化1.二进制数转换成十进制数方法:把二进制各数位的权和该位上的数码相乘,乘积逐项相加。
注意:整数部分权由0,1,2依次展开,小数部分权由-1,-2依次展开。
遇0时可以省略,因为0乘以任何数都为0。
例题:把二进制111010和101.101转换成十进制数。
(111010)2=1ⅹ25+1ⅹ24+1ⅹ23+1ⅹ21=(58)10(101.101)2=1ⅹ22+1ⅹ20+1ⅹ2-1+1ⅹ2-3=(5.625)102.十进制数转换成二进制数方法:整数部分“除2取余法”,小数部分“乘2取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制205.8125转换成二进制数。
整数部分205转换过程如下:小数部分0.8125转换过程如下:(205.8125)10=(11001101.1101)23.十进制数转换成八进制数方法:整数部分“除8取余法”,小数部分“乘8取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制1645.6875转换成八进制数。
(1645.6875)10=(3155.54)84.十进制数转换成十六进制数方法:整数部分“除16取余法”,小数部分“乘16取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制205.21875转换成十六进制数。
(205.21875)10=(CD.38)165.十六进制数和八进制数转换成二进制数方法:十六进制和八进制到二进制分别为24和23,因此,把十六进制和八进制数的每一个数码转成3位和4位的二进制即可.注意:整数前的高位O和小数后的低位O可以去掉。

计算机常用数制之间的转换计算机常用的数制有二进制、八进制、十进制和十六进制。
这些数制之间可以相互转换,常见的转换方式如下:1. 二进制与八进制的转换由于八进制每位可以表示三个二进制数位,因此二进制数转换为八进制数时,只需将二进制数从右往左每三位分一组,然后将每组二进制数转换成对应的八进制数,就可以得到八进制数了。
例如,将二进制数1101011010转换为八进制数,首先将其从右往左每三位分组,得到110 101 101 0,然后将每组二进制数按照下表转换为对应的八进制数:二进制数八进制数000 0001 1010 2011 3100 4101 5110 6根据上表可知,110对应6,101对应5,101对应5,0对应0,因此1101011010转换成八进制数为6550。
2. 二进制与十六进制的转换由于十六进制每位可以表示四个二进制数位,因此二进制数转换为十六进制数时,只需将二进制数从右往左每四位分一组,然后将每组二进制数转换成对应的十六进制数,就可以得到十六进制数了。
例如,将二进制数1101011010转换为十六进制数,首先将其从右往左每四位分组,得到11 0101 1010,然后将每组二进制数按照下表转换为对应的十六进制数:二进制数十六进制数0000 00001 10010 20011 30100 40101 50110 60111 71001 91010 A1011 B1100 C1101 D1110 E1111 F根据上表可知,11对应B,0101对应5,1010对应A,因此1101011010转换成十六进制数为BA。
3. 八进制与十六进制的转换八进制数与十六进制数之间的转换,需要先将八进制数转换成二进制数,然后再将二进制数转换成对应的十六进制数。
例如,将八进制数356转换成十六进制数,首先将其转换为二进制数,得到011 101 110,然后将每组二进制数按照上面的表格转换为对应的十六进制数,得到1DE,因此356转换成十六进制数为1DE。
1 计算机中的常用数制进位计数制,按进位的原则计数,超过基数,向左边进位。
日常生活中有10进制、60进制……计算机中有2进制、8进制、16进制等。
1.1 常用的数制数字66是几?先要确定它是几进制数。
在进位计数制中有数位、基数和位权三个要素。
✧数位:是指数码在一个数中所处的位置。
对于任意禁止—J进制,J个数字符号,逢J进一。
例如十进制,逢十进一;✧基数:是指在某种进位计数制中,每个数位上所能使用的数码的个数。
例如十进制,0,1,2,3,4,5,6,7,8,9。
✧位权:在一个形成数的数码序列中,各位上的基数的幂有所不同。
例如十进制数,各数位的位权(由右至左)分别为100,101,102,……最常见,最熟悉的是10进制;计算机用2进制;8进制和16进制都是从2进制“派生”出来的。
1.2数制转换二←→十进制之间的转换是基础。
1)非十进制→十进制a n ...a1a0.a-1...a-m (r) = a n×r n+ …+ a1×r1 + a0×r0 +a-1×r-1+...a-m×r-ma i是某一位上的数码,r是基数,r i是权。
不同的基数,表示是不同的进制数。
r 进制转化成十进制:数码乘以各自的权的累加例:10101=1×24+1×22+1×20=21101.11(B)=22+1+2-1+2-2=5.75101(O)=82+1=6571(O)=7x8+1=57101A(H)=163+16+10=4106注:(B)—表示该数是二进制数;(O)—表示该数是八进制数;(H) —表示该数是16进制数2) 十进制数→非十进制整数部分和小数部分分别计算。
整数—除2取余,到0为止;小数—乘2取整,到0或满足精度为止。
最先算出的数离小数点近。
例:将十进制数转换成二进制数,小数部分和整数部分分别转换:整数部分:小数部分:2 100 0.6252 50 0 离小数点近× 22 25 0 离小数点近1 1.2502 12 1 × 22 6 0 0 0.502 3 0 × 22 1 1 1 1.00 1100.625=1100100.1013) 二、八、十六进制数制间的转换等价关系,3位二进制数对应1位8进制数;4位二进制数对应1位16进制数。
1在计算机中,常用的数制是________。
A(A)、二进制(B)、十六进制(C)、八进制(D)、十进制2在WORD编辑文档时,选择某一段文字后,把鼠标指针置于选中文本的任一位置,按鼠标左键拖到另一位置上才放开鼠标。
那么,刚才的操作是________。
C(A)、删除文本(B)、复制文本(C)、移动文本(D)、替换文本3 软磁盘和硬磁盘都是______。
A(A)、计算机的外存储器(B)、备用存储器(C)、计算机的内存储器(D)、海量存储器4 用户启动“开始”按钮后,会看到“开始”菜单中包含一组命令,为了显示最近使用过的文档清单,用户必须单击_________命令。
C(A)、“查找”(B)、“程序”(C)、“文档”(D)、“运行”5 在 Excel 工作画面上,“状态栏”是在屏幕的_________。
A(A)、下面(B)、左面(C)、上面(D)、右面6 为了区别“数字“与“数字字符串“数据,Excel 要求在输入项前添加_____C_符号来区别。
(A)、 #(B)、 "(C)、 '(D)、 @7 在微型计算机系统中,微处理器又称为____C__。
(A)、 RAM(B)、 ROM(C)、 CPU(D)、 VGA8 下面4个数中最小的是___A_____。
(A)、 (217)10(B)、 (332)8(C)、 (DB)16(D)、 (11011100)29 关闭当前的Word文档不可采用如下的办法:D(A)、按[Alt]+F4键(B)、鼠标单击当前窗口右上角的[×]按钮(C)、鼠标单击“文件/关闭”(D)、按[Ctrl]+S键10 在WORD中,什么情况下,会出现“另存为”对话框?A(A)、当对文档的存盘采用"另存为"命令方式时(B)、当对文档的第二次及以后的存盘采用快捷键[Ctrl+S]命令方式时(C)、当对文档的第二次及以后的存盘采用"保存"命令方式时(D)、当对文档的第二次及以后的存盘单击工具栏的"磁盘"图标按钮时11 将Word文档的连续两段合并成一段,可使用以下哪些键? B(A)、 [Ctrl](B)、 [Backspace](C)、 [Esc](D)、 [Enter]12 WORD文档中,要将其中一部分内容移动到文中的另一位置,不需要进行下列操作中的哪项?D(A)、粘贴(B)、选择文本块(C)、剪切13 WORD中合并单元格的正确操作是___C_____。
数数值数字数制
数是人类用来计量和表达数量的概念。
它是由数字构成的。
数字是一种用来表示数值的符号或字符。
数制是一种将数值表示为特定的数字系统的方法。
在日常生活中,我们常用的是十进制数制,即使用10个不同的数字来表示数值,其中包括0、1、2、3、4、5、6、7、8和9。
这是因为我们的手指数过程中,使用的是十个手指来计数。
除了十进制数制外,还存在其他一些常用的数制。
其中最常见的是二进制数制,它使用两个数字0和1来表示数值。
二进制数制在计算机科学中非常重要,因为计算机中的所有数据都以二进制形式进行存储和处理。
此外,还有八进制数制和十六进制数制。
八进制数制使用八个数字0到7,而十六进制数制则使用十六个数字0到9以及字母A到F来表示数值。
八进制和十六进制数制常用于计算机编程和网络传输中。
总结而言,数、数值、数字和数制都是用来表示和处理数量的概念和工具。
通过不同的数制,我们能够更加灵活和有效地进行数值的表达和计算。
计算机中的数制在数字计算机中,每个数字和字符都是由一系列的电脉冲信号表示的。
在计算机中电路有脉冲时表示“1”,否则表示“0”。
因此,可以用一连串的“0”、“1”代码来表示数字和字符,这样表示的数据容易移动和存储。
一、数制1.基本概念表示数的方法称为数制。
通常人们习惯以十进制来计量事物,但在生活中也使用其他的数字系统。
例如:月与年使用12进制来计算。
十进制是我们最熟悉的进制,以十进制为例介绍数制的相关概念。
(1)数码:十进制有0~9十个数字符号组成,0~9这些数字符号称为“数码”。
(2)基数:全部数码的个数称“基数”,十进制的基数为10。
(3)计数原则:“逢十进一”。
即用“逢基数进位”的原则计数,称为进位计数制。
(4)位权:数码所处位置的计数单位为位权,位权的大小以基数为底。
例如,十进制的个位的位权是100,十位上的位权为101,百位上的位权为102,以此类推。
而在小数点后第1位上的位权为10-1。
由此可见,各位上的位权值是基数10的若干次幂。
例如,十进制数234.13用位权表示为:常用计数制的基数、位权和数字符号如表1所示。
表1 常用数制的基数、位权和数字符号常用数制的表示方法如表2所示。
表2 常用数制的表示方法二、数制转换1. r进制转换为十进制基数为r的数字,只要将各位数字与它的权相乘,然后按照逢十进位的算法求和,即可将其转换成十进制数。
方法:按位权展开并求和。
(ai为第i位上的数码,r为基数)(a n…a1a0.a-1…a-m)r=a n×r n+…+a1×r1+a0×r0+a-1×r-1+…+a-m×r-m【例1】(11011.1011)2=1×24+1×23+0×22+1×21+1×20+1×2-1+0×2-2+1×2-3+1×2-4=16+8+2+1+0.5+0.125+0.0625=(27.6875)10【例2】(576.5)8 =5×82+7×81+6×80+5×8-1=320+56+6+0.625=(382.625)10【例3】(1B2A.5)16=1×163+11×162+2×161+10×160+5×16-1=4096+2816+32+10+0.31=(6954.31)102.十进制转换为r进制将十进制数转换为r进制数,可将整数部分与小数部分分别转换,然后相加。