工程图学基础A教案-2点线面投影
- 格式:doc
- 大小:6.60 MB
- 文档页数:25



第二节直线的投影在图学中一般用线段表示直线,图学中讲的直线主要是指中学定义的线段,较少指直线,很少指射线,一般混称为直线。
具体指那种,要具体问题具体分析。
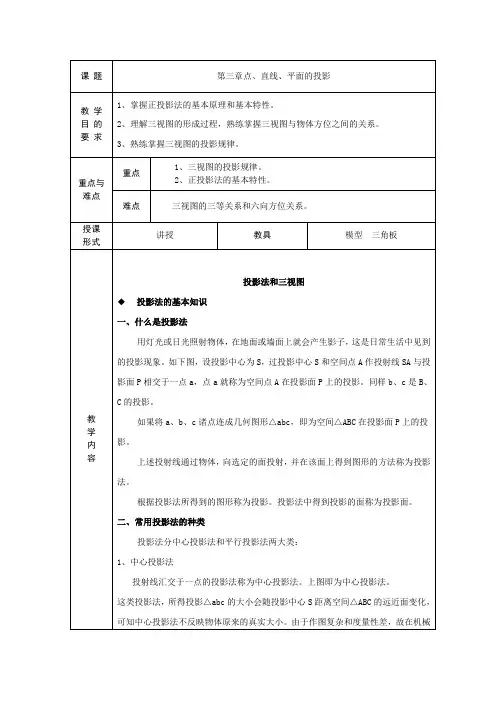
ABabCDc (d)如何求出直线的投影?直线的投影一般仍为直线;当直线垂直于投影面时,其投影积聚为一点,称其在该投影面上具有积聚性。
H同面投影——不同的几何元素在同一投影面上的投影一、直线对投影面的各种相对位置1. 一般位置直线——倾斜于三个投影面的直线2. 投影面平行线——仅平行于一个投影面的直线3. 投影面垂直线——垂直于一个投影面的直线后两类统称为特殊位置直线直线与H、V和W三个投影面的夹角称为直线对投影面的倾角αβγ分别用、、表示Xa'abY HWb''Ob'a''ZY b''YZa''bb'BA Va a'XO HW αβγ1.一般位置直线的投影(1)线段在各投影面上的投影长度小于线段的实长。
(2)直线的各投影均倾斜于投影轴αcos AB ab =βcos AB b a =''γcos AB b a =''''细实线粗度:0.2~0.3mm 粗实线粗度:0.5~0.7mm2. 投影面的平行线定义:仅平行于一个投影面的直线,称为投影面平行线。
平行于H面的直线称为水平线平行于V面的直线称为正平线平行于W面的直线称为侧平线aB b'V HAbb''a''YW Oa'XHab'bY Wb''a''ZY Oa'Xγβ(1)水平线1、ab=AB2、反映β、γ实角3、a ’b’//OX 轴a’’b’’//OY W 轴保真的投影与轴的夹角反映空间直线对相应面的倾角。
另外两个投影平行于相应的投影轴。
H XWH VYββb''YZa''bb'B AH Va a'XOWγY WY HZa''bb'aa'Oαb''(2)正平线1、a’b’=AB2、反映α、γ实角3、ab//OX 轴a’’b’’//OZ 轴γY WY HZa''bb'aa'Oαb''正平线Hab'bY Wb''a''ZY Oa'X γβ水平线典型特征及对比(3)侧平线b''YZb’AHVa a'XOW B a''b Wb''Y YHZa''bb'a a'XOαβ1、a’’b’’=AB2、反映α、β实角3、a ’b’//OZ 轴ab//OY H 轴投影面平行线投影性质:投影面平行线在其所平行的投影面上的投影反映线段的实长;与投影轴的夹角反映直线对相应投影面的倾角;线段的另两个投影平行于相应的投影轴,且小于实长。


【教学内容与过程设计】教学内容过程设计一、点在一个投影面上的投影图1 图2过空间点A向投影面H 引垂线,得到的垂足a即为空间点A在H面上的正投影,见图1。
在投影线任取一点B,,其在H面上的投影与A的投影重合。
结论:在一定的投影条件下,空间一点有其唯一确定的投影,投影a 有无数个空间与其对应。
二、点在两投影面体系中的投影引入:点在一个投影面上的投影能不能确定点的空间位置?(图2)如何解决?——增加投影面。
1、两投影面体系(图3)在图1的基础上再增加一个投影面,处于正面直立位置且与H面相互垂直,这样就建立两投影面体系。
水平投影面——H面;正面投影面——V面;OX投影轴。
图3 图4 ★黑板上画出空间示意图(由图1逐步演变为图3)。
点对一个投影面的投影(图1)点在两投影面体系中的投影(图3)点在三投影面体系中的投影(图5)2、空间点A在两个投影面上的投影(图3)过空间点A分别向H、V面引垂线,得到的垂足a、a'分别为空间点A在H-V两面投影体系中的投影。
A —空间点;a—点A的水平投影;a'—点A的正面投影;3、投影面的展开(图3)为了方便表达,需要将两个相互垂直的投影面展开到同一平面内。
规定:V面保持不动,H面向下旋转90°,使得H面和V面处于同一平面内,从而得到点的两面投影图。
注意:a、a'、a x三点共线,并且垂直OX轴。
4、点的两面投影规律①a'a⊥OX轴,点的水平投影与正面投影的连线垂直于OX轴;②aa x =A a',a'a x=A a,点的水平投影到X轴距离反映该点到V面距离,点的正面投影到X轴距离反映该点到H面距离。
注意:给了点的水平投影和正面投影就可确定该点的空间位置,同样给了一个空间点就有唯一一组水平投影和正面投影与其对应。
A (a,a')三、点在三投影面体系中的投影引入:点的两面投影已经能确定该点的空间位置,但为更清楚地表达某些几何体的形状和结构,需采用三面投影图。


【教学内容与过程设计】教学内容过程设计一、点在一个投影面上的投影图1 图2过空间点A向投影面H 引垂线,得到的垂足a即为空间点A在H面上的正投影,见图1。
在投影线任取一点B,,其在H面上的投影与A的投影重合。
结论:在一定的投影条件下,空间一点有其唯一确定的投影,投影a 有无数个空间与其对应。
二、点在两投影面体系中的投影引入:点在一个投影面上的投影能不能确定点的空间位置?(图2)如何解决?——增加投影面。
1、两投影面体系(图3)在图1的基础上再增加一个投影面,处于正面直立位置且与H面相互垂直,这样就建立两投影面体系。
水平投影面——H面;正面投影面——V面;OX投影轴。
图3 图4 ★黑板上画出空间示意图(由图1逐步演变为图3)。
点对一个投影面的投影(图1)点在两投影面体系中的投影(图3)点在三投影面体系中的投影(图5)2、空间点A在两个投影面上的投影(图3)过空间点A分别向H、V面引垂线,得到的垂足a、a'分别为空间点A在H-V两面投影体系中的投影。
A —空间点;a—点A的水平投影;a'—点A的正面投影;3、投影面的展开(图3)为了方便表达,需要将两个相互垂直的投影面展开到同一平面内。
规定:V面保持不动,H面向下旋转90°,使得H面和V面处于同一平面内,从而得到点的两面投影图。
注意:a、a'、a x三点共线,并且垂直OX轴。
4、点的两面投影规律①a'a⊥OX轴,点的水平投影与正面投影的连线垂直于OX轴;②aa x =A a',a'a x=A a,点的水平投影到X轴距离反映该点到V面距离,点的正面投影到X轴距离反映该点到H面距离。
注意:给了点的水平投影和正面投影就可确定该点的空间位置,同样给了一个空间点就有唯一一组水平投影和正面投影与其对应。
A (a,a')三、点在三投影面体系中的投影引入:点的两面投影已经能确定该点的空间位置,但为更清楚地表达某些几何体的形状和结构,需采用三面投影图。
图5 图61、三投影面体系(图5)在原两投影面体系基础上再增加一个与水平投影面和正面投影面均垂直的投影面,称为侧立投影面(V面),三个投影面均相互垂直。
2、空间点A在三个投影面上的投影(图5)a ——点A的水平投影;a'——点A的正面投影;a"——点A的侧面投影;规定:空间点一律用大写字母表示,点的投影一律用相同小写字母表示,H面投影不加撇,V面投影加一撇,W面投影加两撇。
★在黑板上画出点的两面投影图,然后再转化为三面投影图(由图4演变为图6)。
★第⑵条投影规律可用空间示意图和两面投影图对比说明。
3、投影面的展开(图5)同样,为了表达的方便,需要将空间示意图展开为平面图。
规定:V面保持不动,H面向下旋转90度,W面向右旋转90度,使得三个投影处于同一平面内,Y轴随H面旋转式以Y H表示,Y轴随W面旋转时以Y W表示。
4、点的坐标与三面投影的关系(图5,图6,图7)aa y = a'a z = A a" = X A ⑴aa x = a"a z = A a' = Y A ⑵a'a x = a"a y = A a = Z A ⑶图7结论:只要给出点的空间坐标,就可画出其三面投影图。
5、点的三面投影规律(图6)①点的水平投影与正面投影的连线垂直于OX投影轴,它们共同反映空间点A的X坐标。
即,aa'⊥OX X A②点的侧面投影与正面投影的连线垂直于OZ投影轴,它们共同反映空间点A的Z坐标。
即,a'a"⊥OZ Z A③点的水平投影到X轴的距离和侧面投影到Z轴的距离相等,且都反映该点Y坐标。
即,aa x =a"a z Z A结论:根据点的投影规律,给出点的任意两个投影都可作出第三个投影。
三面投影作图应注意的事项:①投影之间连线一律用细实线;②在图中哪些可以省略,哪些不能省略需要提示。
例1:已知A点的坐标值A(20,15,10),求作A点的三面投影。
★利用点的三面投影的空间示意图和三面投影图重点说明:①点到面的距离、投影到投影轴的距离与点的坐标之间的关系。
②图6所表达的点的三面投影图并不完整,在研究了式⑵后,还应将aa x= a"a z在三面投影图中表达清楚,由图6演变为图7,至此点的三面投影图就表达完整了。
★点的三面投影规律可用空间示意图和三面投影图对比说明来讲解,重点从作图角度来讲从而得出结论…。
★用两个用实例加深对点的三面投影的相关概念的理解。
★例1主要运用点的坐标与三面投影的关系来作图例2:已知点A的两个投影a, a", 求第三投影a′。
四、各种位置点的投影1. 一般位置点(x, y, z)2. 特殊位置点①原点上的点: (0,0,0)②投影轴上点:X 轴上点(x, 0, 0)Y 轴上点(0, y, 0)Z 轴上点(0, 0, z)③投影面上的点:V面上点(x, 0, z)H面上点(x, y, 0)W面上点(0, y, z)注意:点的各个投影一定要写在它所属的投影面区域内。
★例2主要运用点的三面投影规律来作图,其中:⑴a、a"连线垂直于OZ投影轴;⑵aa x = a a z★此处在结合点的三面投影的空间示意图在黑板上举例说明特殊位置点的三面投影的画法例3:已知点的坐标,A( 15, 8, 10 ), B( 15, 8, 0 ), C(15, 0, 0 ),求其三面投影。
五、两点的相对位置与重影点图81. 两点的相对位置(图8)两点的相对位置指两点在空间的前后、左右、上下位置关系。
两点间的相对位置可用它们同方向的坐标差来判断:2. 重影点(图9、图10)空间两点在某一投影面上的投影重合为一点时,则称此两点为对该投影面的重影点。
图9图10例4: 已知B点的三投影,A点在B点之右8毫米,之前5毫米,之上9毫米,求A点的投影。
图10例5: 已知点B距离点A为15,点C点A是对V面的重影点,点D在点A的正下方20。
补全各点的三面投影,并表明可见性。
★此处强调重影点有两个要素:①空间两点②对某一投影面例4选做例5板书讲解【教学内容与过程设计】教学内容过程设计一、直线对一个面的投影直线的投影一般情况下仍为直线,特殊情况下可以投影成一个点。
直线的投影可由直线上任意两点(通常取直线的两端点)的同面投影连线来确定。
根据直线对投影面的相对位置,分为以下三种情况:二、各种位置直线的投影直线在三个投影面中的投影特性取决于直线与三个投影面间的相对位置。
1. 一般位置直线(一般线、倾斜线)与三个投影面都倾斜的直线称为一般位置直线,与三个投影的夹角分别为αβγ。
★用PPT 展示。
★此处应说明αβγ分别对应直线与水投影特性:三个投影都不反映实长,且都小于空间线段的实长;αcos AB ab = βcos AB b a ='' γcos AB b a =''''三个投影都倾斜于投影轴,且与投影轴的夹角都不反映该直线对投影面的倾角。
2. 投影面平行线平行于某一投影面且与其余两个投影面倾斜的直线称为投影面平行线。
① 正平线(∥V 面,对H 、W 面倾斜)投影特性: a 'b '=AB; ab //OX 、a "b "//OZ;a 'b '与OX 和OY 夹角α、γ等于AB 对H 、W 面的倾角。
② 水平线(∥H 面,对V 、W 面倾斜)平投影面、正面投影面、侧面投影面的倾角★此处首先明确指出投影面平行线的定义中“平行于某一投影面”和“倾斜于其余两个投影面”是并列条件,缺一不可。
★对正平线的投影特性逐条分析并得出结论。
《工程图学基础 A》课程教案第二章 点、直线、平面的投影投影特性: ab=AB; abOX、abOY; ab 与 OX 和 OY 夹角β、γ等于 AB 对 V、W 面的倾角。
③ 侧平线(∥W 面,对 H、V 面倾斜)对于水平线和侧 平线可以先用实物 (比如教鞭)摆出 相应的位置,由同 学想象并自己总结 得出其投影特性。
投影特性:ef=EF; efOY、efOZ; ef与 OY 和 OZ 夹角α、β等于 EF 对 H、V 面的倾角。
3. 投影面垂直线 垂直于某一投影面从而与其余两个投影面平行的直线称为投影面垂直 线。
① 正垂线(⊥V 面,∥H、W 面)★对正垂线的投影 特性逐条分析并得 出结论。
对于铅垂线和侧垂线可以先用实物(比如教鞭)摆出相应的位置,由同学想象并自己总结得出其投影特性。
投影特性:11《工程图学基础 A》课程教案正面投影 a(b)积聚为一点; ab=ab=AB; abOX,abOZ。
② 铅垂线(⊥H 面,∥V、W 面)第二章 点、直线、平面的投影投影特性: 水平投影 a(b)积聚为一点; ab=ab=AB; abOX,abOY。
③ 侧垂线(⊥W 面,∥H、V 面)投影特性: 侧面投影 e(f)积聚为一点; ef=ef=EF; efOY,efOZ。
例 1 判断各直线对投影面的相对位置课堂提问12《工程图学基础 A》课程教案第二章 点、直线、平面的投影三、直线上的点 直线上的点有以下投影特性: 从属性--点在直线上,则点的各个投影必在直线的同面投影上,反之,点的各个投影在直线的同面投影上,则该点一定在直线上。
定 比 性 -- 直 线 上 的 点 分 割 线 段 之 比 等 于 其 投 影 之 比 。
即 ,AC:CB=ac:cb=ac:cb=ac:cb。
例 1 已知直线 AB 两面投影和点 K 的正面投影, K 点在 AB 上,补全 K 例 1 主要运用从属点的三面投影。
性来作图,强调两点:① 作图顺序。
首先根据已知的直线的两个投影将第三投影作出。
② 对于一般位置例 2 已知直线 AB 和点 K 的正面和水平投影,判断点 K 在线段 AB 上?直线上的点,直接 运用点的投影规律就能求得点的其他投影。
方法一(用第三面投影验证)方法二(用定比性来作图)13★例 2 主要运用定 比性来作图。
强调 侧平线上的点不能 直接运用点的投影 规律。
方法一不在 黑板上作图示意, 仅介绍。
★例 1 和例 2 在黑 板上作图时并列放《工程图学基础 A》课程教案第二章 点、直线、平面的投影注意:一般位置直线可以在两面投影上通过从属性来判断,对于特殊位置直线有 在一起,以便同学时还需要通过第三面投影或定比性进行判断。
对比。
四、两直线的相对位置1. 平行两直线空间两直线平行,则其各组同面投影必相互平行,并且两平行线段之比等于它们的同面投影之比。
反之,若两直线的各同面投影互相平行,则空间两直线平行。