三角形荷载分布荷载合力作用点

第三章土中应力计算一、填空题1.由土筑成的梯形断面路堤，因自重引起的基底压力分布图形是梯形，桥梁墩台等刚性基础在中心荷载作用下，基底的沉降是相同的。

2.地基中附加应力分布随深度增加呈曲线减小，同一深度处，在基底中心点下，附加应力最大。

3.单向偏心荷载作用下的矩形基础，当偏心距e > l/6时，基底与地基局部脱开，产生应力重分部。

4.在地基中，矩形荷载所引起的附加应力，其影响深度比相同宽度的条形基础浅，比相同宽度的方形基础深。

5.上层坚硬、下层软弱的双层地基，在荷载作用下，将发生应力扩散现象，反之，将发生应力集中现象。

6.土中应力按成因可分为自重应力和附加应力。

7.计算土的自重应力时，地下水位以下的重度应取有效重度（浮重度）。

8.长期抽取地下水位，导致地下水位大幅度下降，从而使原水位以下土的有效自重应力增加，而造成地基沉降的严重后果。

9.饱和土体所受到的总应力为有效应力与孔隙水压力之和。

二、名词解释1.基底附加应力：基底压应力与基底标高处原土层自重应力之差。

2.自重应力：由土层自身重力引起的土中应力。

3.基底压力：建筑物荷载通过基础传给地基，在基础底面与地基之间的接触应力。

三、选择题1.成层土中竖向自重应力沿深度的增大而发生的变化为：（B ）（A）折线减小（B）折线增大（C）斜线减小（D）斜线增大2.宽度均为b，基底附加应力均为P0的基础，同一深度处，附加应力数值最大的是：（C ）（A）方形基础（B）矩形基础（C）条形基础（D）圆形基础（b为直径）3.可按平面问题求解地基中附加应力的基础是：（B ）（A）柱下独立基础（B）墙下条形基础（C）片筏基础（D）箱形基础4.基底附加应力P0作用下，地基中附加应力随深度Z增大而减小，Z的起算点为：（A ）（A）基础底面（B）天然地面（C）室内设计地面（D）室外设计地面5.土中自重应力起算点位置为：（B ）（A）基础底面（B）天然地面（C）室内设计地面（D）室外设计地面6.地下水位下降，土中有效自重应力发生的变化是：（A ）（A）原水位以上不变，原水位以下增大（B）原水位以上不变，原水位以下减小（C）变动后水位以上不变，变动后水位以下减小（D）变动后水位以上不变，变动后水位以下增大7.深度相同时，随着离基础中心点距离的增大，地基中竖向附加应力：（D ）（A）斜线增大（B）斜线减小（C）曲线增大（D）曲线减小8.单向偏心的矩形基础，当偏心距e < l/6（l为偏心一侧基底边长）时，基底压应力分布图简化为：（B ）（A）矩形（B）梯形（C）三角形（D）抛物线形9.宽度为3m的条形基础，作用在基础底面的竖向荷载N＝1000kN/m ，偏心距e＝0.7m，基底最大压应力为：（C ）（A）800 kPa （B）417 kPa （C）833 kPa （D）400 kPa10.矩形面积上作用三角形分布荷载时，地基中竖向附加应力系数K t是l/b、z/b的函数，b指的是：（D ）（A）矩形的长边（B）矩形的短边（C）矩形的短边与长边的平均值（D）三角形分布荷载方向基础底面的边长11.某砂土地基，天然重度γ＝18 kN/m3，饱和重度γsat＝20 kN/m3，地下水位距地表2m，地表下深度为4m处的竖向自重应力为：（A ）（A）56kPa （B）76kPa （C）72kPa （D）80kPa12.均布矩形荷载角点下的竖向附加应力系数当l/b＝1、Z/b＝1时，K C＝0.1752；当l/b＝1、Z/b＝2时，K C＝0.084。

工程力学（一）期末复习题一、填空题1. 在材料力学中，为了简化对问题的研究，特对变形固体作出三个假设，分别为 ， ， 。

答案：连续性，均匀性，各向同性2. 图中分布力的合力的大小为 ，对点A 之矩大小为 。

答案：/2()ql ↓，2/3ql (顺时针)知识点解析：本题考查分布力大小及合力作用点的计算，三角形分布力合理大小为三角形的面积，合力作用点为形心处。

3. 将圆截面压杆改为面积相等的圆环截面压杆，其他条件不变，则其柔度将 ，临界荷载将 。

答案：降低，增大知识点解析：本题考查压杆柔度和临界荷载与截面形状的关系，将圆截面压杆改为面积相等的圆环截面压杆，截面惯性矩增大，柔度降低而临界荷载增大。

4. 对于空间力偶系，独立的平衡方程个数为 。

答案：3个知识点解析：空间力偶系独立平衡方程的个数5. 解决超静定问题需要采用变形体模型，进行力、变形以及 关系的研究三方面的分析工作。

答案：力与变形6. 图示销钉受轴向拉力P 作用，尺寸如图所示，则销钉内的剪应力τ= ，支承面的挤压应力bs σ= 。

答案：P dh π，()224P D d π-知识点解析：本题考查连接件剪应力与挤压应力的计算。

7. 一受扭圆棒如图4所示，其m －m 截面上的扭矩等于 ，若该圆棒直径为d ，则其扭转时横截面上最大切应力max = 。

图4答案：M -，348M d π 知识点解析:本题考查圆轴扭转时扭矩和切应力的计算方法，首先取隔离体，根据扭矩平衡和右手螺旋法则计算出m －m 截面的扭矩为M -，根据切应力计算公式计算出截面的最大切应力max =348M d π。

8. 图5示阶梯杆AD 受三个集中力F 作用，设AB 、BC 、CD 段的横截面面积分别为A 、2A 、3A ，则三段杆的横截面上轴力 ，正应力 。

图5答案：不相等，相等知识点解析：本题考查受拉杆件内力和应力的计算，首先分段取隔离体计算出AB 、BC 、CD三段杆所受轴力分别为F 、2F 、3F ，正应力为轴力除以受力面积，三段杆正应力均为F/A 。

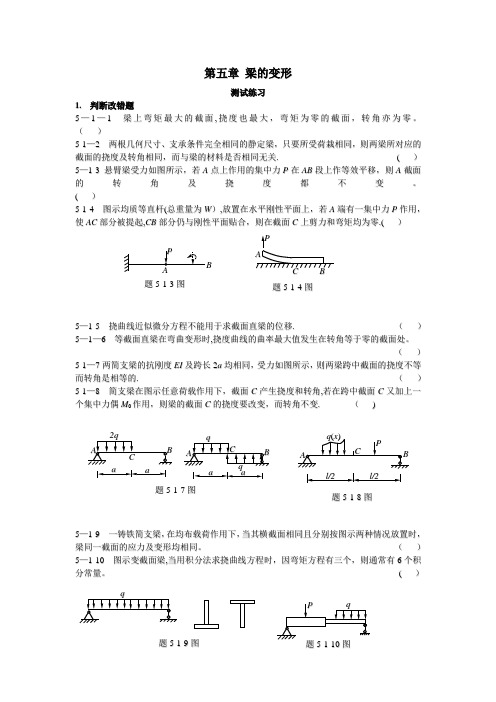
第五章 梁的变形测试练习1. 判断改错题5—1—1 梁上弯矩最大的截面,挠度也最大，弯矩为零的截面，转角亦为零。

（ ）5-1—2 两根几何尺寸、支承条件完全相同的静定梁，只要所受荷栽相同，则两梁所对应的截面的挠度及转角相同，而与梁的材料是否相同无关. ( ） 5—1-3 悬臂梁受力如图所示，若A 点上作用的集中力P 在A B 段上作等效平移，则A 截面的转角及挠度都不变。

( ）5-1-4 图示均质等直杆(总重量为W ）,放置在水平刚性平面上，若A 端有一集中力P 作用，使A C 部分被提起,C B 部分仍与刚性平面贴合，则在截面C 上剪力和弯矩均为零.( ）5—1-5 挠曲线近似微分方程不能用于求截面直梁的位移. （ ） 5—1—6 等截面直梁在弯曲变形时,挠度曲线的曲率最大值发生在转角等于零的截面处。

（ ） 5-1—7两简支梁的抗刚度E I 及跨长2a 均相同，受力如图所示，则两梁跨中截面的挠度不等而转角是相等的. （ ） 5-1—8 简支梁在图示任意荷载作用下，截面C 产生挠度和转角,若在跨中截面C 又加上一个集中力偶M 0作用，则梁的截面C 的挠度要改变，而转角不变. （ )5—1-9 一铸铁简支梁，在均布载荷作用下，当其横截面相同且分别按图示两种情况放置时，梁同一截面的应力及变形均相同。

（ ） 5—1-10 图示变截面梁,当用积分法求挠曲线方程时，因弯矩方程有三个，则通常有6个积分常量。

( ）题5-1-3图题5-1-4图题5-1-8图题5-1-7图题5-1-9图2．填空题5-2—1 挠曲线近似微分方程EIx M x y )()("-= 的近似性表现在和。

5—2-2 已知图示二梁的抗弯度E I 相同,若使二者自由端的挠度相等，则=21P P 。

5-2-3 应用叠加原理求梁的变形时应满足的条件是：。

5-2—4 在梁的变形中挠度和转角之间的关系是。

5—2-5 用积分法求图示的外伸梁(B D 为拉杆)的挠曲线方程时，求解积分常量所用到的边界条件是，连续条件是.5—2-6 用积分法求图示外伸梁的挠曲线方程时，求解积分常量所用到边界条件是，连续条件是。

理论力学三角形载荷的计算公式
1、均匀分布载荷f、dx dy上的力fdxdy是常数、其产生的力矩为xfdxdy (x轴方向类)、对xfdxdy沿受力面积用二重积分积一下就解决了、如果是园形r 径向类。

力矩为rrdrda,对rrdrda沿受力面积用二重积分积一下一样解决。

对三角形分布在载荷的力和力矩,要确定力矩方向和受力面边界方程。

2、可以将均布载荷看成一个集中力，这个集中力的大小就是均布载荷的面积（q·L），作用于分布区域的中点（L/2）处。

运用均布载荷计算弯矩的公式可以简单认为M=（q*x^2）/2，x是均布载荷的长度。

其来历是：q*x是作用在结构上的合力F，单位为N，合力的作用点位于载荷作用的中点，故F的力臂为x/2米，从而弯矩M=（q*x^2）/2。

力矩在物理学里是指作用力使物体绕着转动轴或支点转动的趋向。

力矩的单位是牛顿-米。

力矩希腊字母是tau。

力矩的概念，起源于阿基米德对杠杆的研究。

转动力矩又称为转矩或扭矩。

力矩能够使物体改变其旋转运动。

推挤或拖拉涉及到作用力，而扭转则涉及到力矩。

力矩等于径向矢量与作用力的叉积。

第一章 土的物理性质及其工程分类P 60[2-2] 解：V=21.7cm 3，m=72.49－32.54＝39.95g ，m S =61.28－32.54＝28.74g ，m W =72.49－61.28=11.21g7.2195.39==V m ρ＝1.84g/ cm 3，74.2821.11==sw m m w ＝39％ 07.1184.1)39.01(174.21)1(=-+⨯⨯=-+=ρωρW S d eP 60[2-3] 解：963.0185.1)34.01(171.21)1(=-+⨯⨯=-+=ρωρWS d e 963.01963.071.21++=++=e e d s sat ρ＝1.87 g/ cm 3，87.0187.1=-=-='W sat ρρρ g/ cm 3g ργ'='＝0.87×10＝8.7 kN/m 3P 60[2-4] 解：已知77.1=ρg/cm 3, w ＝9.8％，s d ＝2.67，461.0min =e ,943.0max =e∴656.0177.1)098.01(167.21)1(=-+⨯⨯=-+=ρωρW S d e ，∈=--=--=6.0461.0943.0656.0943.0min max max e e e e D r （0.33，0.67）∴该砂土处于中密状态。

P 60[2-5] 解：已知s d ＝2.73，w ＝30％，=L w 33％，=P w 17％土样完全饱和→1=r S ，sat ρρ=819.073.23.01=⨯=⇒==e e wd S S r ，819.01819.073.21++=++=e e d s sat ρ＝1.95 g/ cm 3 3.0195.11+=+=w d ρρ＝1.5 g/ cm 3，161733=-=-=P L p w w I 81.0161730=-=-=P P LI w w I 10＜16=p I ≤17→该土为粉质粘土0.75＜81.0=L I ≤1→该土处于软塑状态[附加1-1]证明下列换算公式：（1）w s d e d ρρ+=1；（2）γee S sw r ++=1γγ；（3）n n w S w s r γγ)1(-=（1）证明：设e V V V V V Ve V S V V SV S +=+===⇒=1,1w s s w s s s s d ed V V d V V V m ρρρρ+====1 （2）证明：设e V V V V V Ve V S V V SV S +=+===⇒=1,1V g V V V g m m V mg V G s s w w s w )()(ρργ+=+===ee S V V V S sw r s s w v r ++=+=1γγγγ （3）证明：设n V n V n VVV s v v -==⇒==1,,1∴nn w gV gV w V V w V V m m V m V V S w s v w s s v w s s ss v w s wv w w v w r γγρρρρρρρ)1(-====== [附加1-2]解：V=72cm 3，m=129.5g ，m S =121.5g ，m W =129.5－121.5=8g%6.65.1218===⇒S W m m ω 6.0172/5.129)066.01(17.21)1(=-+⨯⨯=-+=ρωρW S d e %7.296.07.2066.0=⨯==e d S S r ω 0.1872105.129=⨯===V mg V G γkN/m 36.20106.16.07.21=⨯+=++=W S sat e e d γγkN/m 36.10106.20=-=-='W sat γγγkN/m 39.16106.17.21=⨯=+=W S d e d γγkN/m 3∴γγγγ'>>>d sat[附加1-3]解：已知s d ＝2.68，w ＝32％，土样完全饱和→1=r S86.068.232.01=⨯=⇒==e ed S Sr ω02.1986.1)32.01(1068.286.01)1(=+⨯⨯=⇒=-+=γγωγW S d e kN/m 3[附加1-4]解：已知66.1=ρg/cm 3,s d ＝2.69，（1）干砂→w ＝0 ∴62.0166.1)01(169.21)1(=-+⨯⨯=-+=ρρw d e W S（2）置于雨中体积不变→e 不变∴%2.969.262.04.04.0=⨯=⇒==w e wd S S r [附加1-5]解：已知m=180g ，1w ＝18％，2w ＝25％，sss s s w m m m m m m m w -=-==18011＝18％→s m ＝152.54g∴)(12w w m m s w -=∆＝152.54×（0.25－0.18）＝10.68g[附加1-6]实验室内对某土样实测的指标如下表所示，计算表土中空白部分指标。

1.设有矩形截面的竖柱，其密度为ρ，在一边侧面上受均布剪力q ，如图1，试求应力分量。

解：采用半逆解法，设=x σ 。

导出ϕ使其满足双调和方程：0)()(,00,0)()()()()(,0414444224444144444122=+=∇=∂∂∂=∂∂+=∂∂+==∂∂=-∂∂=dxx f d dx x f d yy x y dx x f d dx x f d y x x f x yf x f y Xx y x ϕϕϕϕϕϕϕσ（1）含待定常数的应力分量为：⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫++-=∂∂∂-=-+++=-∂∂==-∂∂=)23(26)26(0222222C Bx Ax y x Py F Ex B Ax y Yy x Xx yxy y x ϕτϕσϕσ （2）（3）x1取任意值时，上式都应成立，因而有：y 23232312341444)()(,)(0)(,0)(Fx Ex Cx Bx Ax y Fx Ex x f Cx Bx Ax x f dx x f d dx x f d ++++=+=++===ϕ式中， 中略去了常数项， 中略去了 的一次项及常数项，因为它们对应力无影响。

)(x f )(1x f x利用边界条件确定常数，并求出应力解答：,0)(0==x x σ 能自然满足： 0,0)(0===C x yx τ,0)(==h x x σ能自然满足：,026,0)(23,)(02===+==--===F E F Ex q Bh Ah q y y h x yx στCyBx y x gy By Ax Yy xDy Cx Xx y xyy x 22266222222--=∂∂∂-=-+=-∂∂=+=-∂∂=ϕτρϕσϕσ0)(,0)(00====y xy y y τσ（4）（5）2．如图2（a ），三角形悬臂梁只受重力作用，梁的密度为，试用纯三次式应力函数求解该梁的应力分量。

2.用边界条件确定常数，进而求出应力解答：上边界：,0)(0==y yx τ不能精确满足，只能近似满足： ⎰⎰=+-===h hy y xy dx Bx Ax dy 000200)23(,0)(τ023=--Bh Ah 由式（3）、（4）解出常数 和 ，进而可求得应力分量： A B hqB h q A =-=,2（)32(,)31(2,0h x h qx Py h x h qy xy y x --=--==τσσxx x 图（a ） （b ）解： 1.设应力函数为： 3223Dy Cxy y Bx Ax +++=ϕ 不难验证其满足 。