“三等角一线型”在几何中的运用(PDF X页)
- 格式:pdf
- 大小:147.18 KB
- 文档页数:3

一线三等角在相似三角形中的应用首先,我们先来看一线三等角的特殊构造:如图,A、D、E在一条直线上,△ABC为等腰直角三角形,∠BAC = 90°,BD⊥DE,CE⊥DE。
这里,我们容易得到:△ABD≌△CAE。
最初形式这个就是一线三等角的最初形式。
然后,我们再看更一般的形式,如果△ABC不是等腰,AB≠AC,如图,这个时候△ABD和△CAE肯定不全等,那么,它们是什么关系呢?很容易,可以得到∠DAB=∠ECA,△ABD∽△CAE,它们相似。
一线三直角注意看这张图,点D、A、E在一条直线上,并构成三个直角,这张图就叫做一线三直角。
注意,是一线三直角,还没进化成一线三等角。
那么,得出它们相似有什么用处呢?当然是得到比例线段,比如AD/BD = CE/AE。
根据比例线段求线段长是这类模型的主要用途。
我们得到一线三直角后,还可以继续探讨。
如果这三个角不是直角,但是它们相等,还能得到相似吗?如图,A、D、E在一条直线上,∠D=∠1=∠E=80°, 我们同样可以得到:△ABD∽△CAE。
道理和之前的差不多。
同样可以得到比例线段。
一线三等角如果把图中三个80°的角变成其他度数的角,同样可以得出相似以及比例线段。
一般地,只要A、D、E在一条直线上,并且,∠BAC=∠D=∠E,我们都有:△ABD∽△CAE这就是一线三等角的一般形式。
进而有比例线段:实际解题时,往往将一线三等角伪装起来,比如包含在等边三角形中。
例1:如图,已知等边△ABC的边长为2,D、E、F分别是AB、BC、CA上的点,并且,BD=1,BE=1/3,∠DEF = 60°,求CF的长。
例1图这里,易得∠DEF =∠B =∠C,构成一线三等角,从而有△BDE∽△CEF,得到BE/BD = CF/CE,很容易可以求出CF的长。
一线三等角可以隐藏在一般的等腰三角形中。
问题的关键就是找出隐藏的一线三等角。
我们再看坐标系中隐藏的一线三等角。

相似三角形基本模型——一线三等角模型模型解读:“一线三等角模型”图谱 (1)点P 在线段AB 上锐角一线三等角直角一线三等角钝角一线三等角 以上有:△ACP ∽△BPD(2)点P 在线段AB 延长线上锐角一线三等角直角一线三等角钝角一线三等角 以上有:△ACP ∽△BPD 模型分析 三个相等的角的顶点在同一直线上,就会形成一组相似三角形,习惯上把该组相似三角形称为“一线三等角型”相似三角形。
典型示例 例1.如图,已知:在Rt △ABC 中,∠ACB=90°,AC=BC=4M 是边AB 的中点,E 、G 分别是边AC 、BC 上的一点,∠=45°,AC 与MG 的延长线相交于点F(1)在不添加字母和线段的情况下写出图中一定相似的三角形,并证明其中的一对(2)联结结EG ,当AE =3时,求EG 的长(3)证明:△MEG ∽△AEM例2.已知:如图,直角梯形ABCD 中,AD ∥BC ,∠B=90AB=8,AD=12,tanC=43 ,AM ∥DC ,E 、F 分别是线段AD AM 上的动点(点E 与A 、D 不重合)且∠FEM=∠AMB ,设DE=x5.如图在△ABC 中,已知AB=AC=5,BC=6,且△ABC ≌△DEF ,将△DEF与△ABC 重合在一起,△ABC 不动,△DEF 运动,并满足:点E 在边BC 上沿B 到C 的方向运动,且DE 始终经过点A ,EF 与AC 交于M 点.(1)求证:△ABE∽△ECM;(2)探究:在△DEF 运动过程中,重叠部分能否构成等腰三角形?若能,求出BE 的长;若不能,请说明理由;(3)当线段AM 最短时,求重叠部分的面积6.已知在梯形ABCD 中,AD//BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图,P 为AD 上的一点,满足∠BPC =∠A . ①求证:△ABP ∽△DPC ②求AP 的长(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出x 取值范围②当CE =1时,写出AP 的长7.已知△ABC 中,角平分线BD ,CD 交于点D ,过D 作直线EF 交AB 于E ,交AC 于F ,且AE=AF (1)求证:AD⊥EF(2)求证:∠BDC=1/2∠A+90°(3)若CF=2,CD=4,BD=6,求BE 的长8.等边△ABC 边长为6,P 为BC 边上一点,∠MPN =60°,且PM 、PN 分别于边AB 、AC 交于点E 、F . (1)如图1,当点P 为BC 的三等分点,且PE ⊥AB 时,判断△EPF 的形状; (2)如图2,若点P 在BC 边上运动,且保持PE ⊥AB ,设BP =x ,四边形AEPF 面积的y ,求y 与x 的函数关系式,并写出自变量x 的取值范围; (3)如图3,若点P 在BC 边上运动,且∠MPN 绕点P 旋转,当CF =AE =2时,求PE 的长.。

全等三角形——一线三等角模型一、一线三等角概念“一线三等角”指的是有三个等角的顶点在同一条直线,这个角可以是直角,也可以是锐角或钝角。
二、一线三等角的类型同侧:锐角 直角 钝角异侧:三、“一线三等角”的性质当∠1=∠2=∠3,且当等角所对的边相等时,则两个三角形全等. 如右图,若 CE=ED ,则△AEC ≌△BDE. 四、“一线三等角”的应用 1.适用于直角的情况例1:在ABC Rt ∆中,︒=∠90ACB ,BC AC =,直线l 经过点C ,且l AE ⊥于点E ,l BF ⊥于点F . (1)当直线l 绕点C 旋转到如图1的位置时,○1图中有几对相等的锐角? ○2求证:AEC ∆≌CFB ∆; ○3试探究AE 、BF 、EF 之间的数量关系,并说明理由; (2)当直线l 绕点C 旋转到如图2的位置时,试探究AE 、BF 、EF 之间的数量关系,并说明理由; (3)当直线l 绕点C 旋转到如图3的位置时,试探究AE 、BF 、EF 之间的数量关系,不必说明理由.图1 图2 图3lFE B ACl FEB AC lFEBAC DCC A BDDC DBADB CAAB2.适用于锐角或钝角的情况例2:如图,在△ABC 中,AB =AC ,BD =CF ,BE =CD , 若∠A =40°,则∠EDF 的度数为( )A. 75°B. 70°C. 65°D. 60°★演练题:(勾股定理)如图,在ABC Rt ∆中,︒=∠90ACB ,BC AC =,点D 为斜边AB 上一点,连接CD ,过点A 作CD AE ⊥于点E .若︒=∠45BED ,4=AE ,则=AB ___________.练习1.如图,ABC ∆是等腰三角形,DE 过直角顶点A ,︒=∠=∠90E D ,则下列结论正确的个数有( ) ○1AE CD =; ○221∠=∠; ○3︒=∠+∠9043; ○4BE AD =; ⑤DE=CD+BE. (A )1个 (B )2个 (C )3个 (D )4个2.(1)已知△ABC 是直角三角形,∠BAC =90°,AB =AC ,直线l 经过点A ,分别从点B 、C 向直线l 作垂线,垂足分别为D 、E .当点B ,C 位于直线l 的同侧时(如图1),易证△ABD ≌△CAE .如图2,若点BC 在直线l 的异侧,其它条件不变,△ABD ≌△CAE 是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.(2)变式一:如图3,△ABC 中,AB =AC ,直线l 经过点A ,点D 、E 分别在直线l 上,点B 、C 位于l 的同一侧,如果∠CEA =∠ADB =∠BAC ,求证:△ABD ≌△CAE .(3)变式二:如图4,△ABC 中,依然有AB =AC ,若点B ,C 位于l 的两侧,如果∠BDA+∠BAC =180°,∠BDA =∠AEC ,求证:BD =CE+DE .4321EB DC AEC DA。

一线三等角模型一线三等角定义:指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,通常称为“K字模型”,也有部分地方称为“M形图”。
起源与基本类型DE绕A点旋转,从外到内,从一般位置到特殊位置。
基本类型同侧“一线三等角”异侧“一线三等角”性质1.一般情况下,如下左图,易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等。
(若CE=ED,则△AEC≌△BDE)3.中点型“一线三等角”如右上图,当∠1=∠2=∠3,且D是BC中点时,△BDE∽△CFD∽△DFE.4.“一线三等角”的各种变式应用1.“一线三等角”应用的三种情况。
a.图形中已经存在一线三等角,直接应用模型解题;b.图形中存在“一线二等角”,补上“一等角”构造模型解题;c.图形中只有直线上一个角,补上“二等角”构造模型解题.2.在定边对定角问题中,构造一线三等角是基本手段。
3.构造一线三等角的步骤:找角、定线、构相似。
如上图,线上有一特殊角,就考虑构造同侧型一线三等角,当然只加这两条线通常是不够的,为了利用这个特殊角与线段的关系,过C、D两点作直线l的垂线是必不可少的。
模型建立例如图2,已知E是矩形ABCD的边AB上一点,EF⊥DE交BC于点F,试说明:ΔADE∽ΔBFE。
分析:要证明ΔADE与ΔBFE相似,已经知道∠A=∠B=90°,只需要再找出另外一对相等的角即可。
解答:在矩形ABCD中,∠A=∠B=90°∵EF⊥DE∴∠DEF=90°,∠2+∠3=90°又∵∠1+∠3=90°∴∠1=∠2∴ΔADE∽ΔBFE小结:此时,在直线AB上,∠A=∠DEF=∠B=90°,一条线上有3个直角,两边的ΔADE与ΔBFE相似。
这个相似的基本图形像字母K,可以称为“K”型相似,但更因为图形的结构特征是一条线上有3个垂直关系,也常被称为“一线三垂直”。
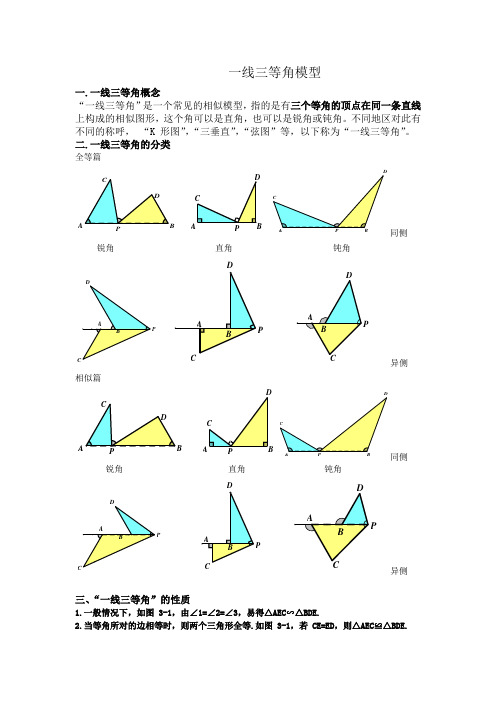
一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.一线三等角的分类全等篇同侧锐角直角钝角P异侧相似篇A同侧锐角直角钝角P异侧三、“一线三等角”的性质1.一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED,则△AEC≌△BDE.3.中点型“一线三等角”如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE.4.“中点型一线三等角“的变式(了解) 如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.如图 3-4“中点型一线三等角”通常与三角形的内心或旁心相关,1902BOC BAC ∠=︒+∠这是内心的性质,反之未必是内心.在图 3-4(右图)中,如果延长 BE 与 CF ,交于点 P ,则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明 )图 3-5其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c.图形中只有直线上一个角,不上“二等角”构造模型解题.体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特殊性如图 3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过 C、D 两点作直线 l 的垂线是必不可少的。

几何模型:一线三等型模角.一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.一线三等角的分类全等篇D D C D C C BA BAP P ABP同侧锐角直角钝角D DDAP A A B P PB BC C C异侧相似篇D D C D C C BA BA P P ABP同侧钝角直角锐角D DDAP A B PB APB C C C异侧三、“一线三等角”的性质BDE.∽△,易得△AEC一般情况下,如图 3-1,由∠1=∠2=∠31.BDE.AEC≌△当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED,则△2.3.中点型“一线三等角”中点时,△BDE∽△CFD∽△DFE.如图 3-2,当∠1=∠2=∠3,且D 是 BC) 了解4.“中点型一线三等角“的变式(1??BOC?BAC90??时,点 O 是△ABC 的内心如图 3-3,当∠1=∠2 且.可以考虑构2造“一线三等角”.如图 3-4“中点型一线三等角”通常与三角形的内心或旁心相关,1?BOC?90???BAC这是内心的性质,反之未必是内心.2在图 3-4(右图)中,如果延长 BE 与 CF,交于点 P,则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明)图 3-5其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用.1.“一线三等角”应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c.图形中只有直线上一个角,不上“二等角”构造模型解题.体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特殊性如图 3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过 C、D 两点作直线 l 的垂线是必不可少的。
中考专题:一线三等角模型的多个用途本文介绍一个基本数学模型,并运用该基本模型的构建来解决问题.一、基本模型如图1,点,,B E C 三点共线,且已知90AEF ECF ABE ∠=∠=∠=︒,易得ABE ECF ∆∆:.当然,如果这两个三角形中只要有一组边对应相等,则有ABE ECF ∆≅∆的结论.此模型中,我们还可以将条件一般化:如图2,若ADE B C α∠=∠=∠=∠,则ABD DCE ∆∆:.我们从上面的图形中可得出一种几何基本模型:“一线三等角”模型.二、用途1.直接用途当图形中出现基本模型时,我们可以直接应用模型高效地解决问题.例1 如图3,已知抛物线与x 轴交于,A B 两点,点A 的坐标为(2,0),它与y 轴交于C 点,点C 的坐标为(0,3),它对称轴是直线4x =. (1)求此抛物线的函数关系式;(2)若抛物线上有一点P ,且90PBC ∠=︒,求点P 坐标.解析 第(1)题易得此抛物线的函数关系式为:21234y x x =-+.第(2)题,我们可以从原图中直接得出基本模型如图4,易证BCO PBD ∆∆:, 所以12DB CO DP BO ==.设BD x =,则2DP x =,∴点P 的坐标为(6,2)x x +. 将其代入抛物线的函数关系式,得212(6)2(6)34x x x =+-++. 解得124,0x x ==(舍),∴点P 的坐标为(10,8).2.补形用途(1)当图形中的基本模型不完整时,我们可以通过添加辅助线补形得出我们需要的模型,再运用模型以便高效地解决问题.例2 如图5,平面内4条直线1l ,2l ,3l ,4l 是一组平行线,每相邻2条平行线间的距离都是1个单位长度.正方形ABCD 的4个顶点,,,A B C D 都在这些平行线上,其中点,A C 分别在直线1l 和4l 上,则此正方形的面积是 .解析 在四条平行线的背景下,我们可以画出符号题意得两个图形,如图6、图7,要求正方形的面积,须先求其边长.图6中的正方形边长显然是3,则其面积为9;而图7可以添加辅助线构建出“一线三等角”模型即可解决问题.如图7,过点D 作1DH l ⊥于点H ,延长HD 交直线4l 于点G ,则Rt ADH Rt DCG ∆≅∆.由“一线三等角”模型,可得1AH DG ==.由于2DH =,根据勾股定理,得, 2225AD AH DH =+=,所以此时正方形面积为5.(2)当图形中没有基本的模型图形时,我们可以考虑“无中生有”,构造出我们需要的基本模型,再运用此基本模型解决问题.例3 如图8,在边长相同的小正方形组成的网格中,点,,,A B C D 都在这些小正方形的顶点上,,AB CD 相交于点P ,则tan APD ∠的值为 .解析 本题求tan APD ∠的值的方法不是唯一的,要求一个角的三角函数值,一般情况下,我们要将其置于一个直角三角形中.本题我们构造“一线三等角”的基本模型是高效的解决方案之一如图9,取格点E ,连结AE ,BE ,可知ABE ∆是等腰直角三角形.过点E 作EF AB ⊥于点F ,由“三线合一”和“直角三角形斜边中线等于斜边的一半”的知识点可得12EF BF AB ==,由题意知//BD AC ,所以13BP BD AP AC ==. 因此1142BP AB BF ==, 即12BP PF BF ==, ∴tan 2EF APD PF ∠==运用建模的数学思想可以将复杂问题简单化,将未知转化为已知,它也能提高我们的数学应用能力和创新能力.我们在解题的过程中,要遵循我们的认知规律:一方面,我们要注意以解决问题为契机建构知识,并学会联系与联想;另一方面,我们应该掌握分析问题的途径,经历思考和选择的过程,从多种方法策略中寻找和筛选合适的解决方案,从而将问题逐步分解加以解决.。
关于“一线三垂直”模型及其在平面几何中的应用“一线三垂直”模型是“一线三等角”模型的特殊情况,(关于“一线三等角”模型详见比例与相似高级教程(六):相似三角形的“一线三等角”模型),即三个等角角度为90o,于是有三组边相互垂直,所以称为“一线三垂直”模型。
“一线三垂直”的性质:1,模型中必定存在至少两个三角形相似,三对等角,三对成比例的边长;2,当模型中有一组对应边长相等时,则模型中必定存在全等三角形。
其中,在“变形2”模型下,根据相似原理,推理出了著名的“射影定理”这里主要讨论有一对对应边相等的情况。
【例1】如图,在等腰直角三角形ABC 中,∠ ACB=Rt ∠,AC=BC ,AE ⊥ CE 于点E,BD ⊥CE 于点 D ,AE=5cm ,BD=2cm ,则DE 的长为多少?一线三垂直”模型在平面几何中有着及其重要的地位,常出现的图例有以下几种:【提示】根据“一线三垂直”模型的性质,△ACE≌△CBD ,于是CD=AE=5cm CE=BD=2cm ,DE=5-2=3 (cm )【例2】如图,在△ ABC 中,CA=CB ,点 D 为BC 中点,CE⊥ AD 于点E,交AB 点F,连接DF 。
求证:AD=CF+DF.则易证△ ACD ≌△ CBG ,于是AD=CG=CF+FG ;BG=CD=BD ,BF=BF ,∠ DBF= ∠ GBF=45o ,故△ BDF ≌△ BGF ,于是FD=FG ,所以AD=CF+DF 。
【解析】此题乍一看起来和【例从要证明的结论来看,需要把BG ⊥ CB ,交CF 的延长线于1】相同,却不能照搬照抄。
AD 这条线段“转化”到直线CF 上。
如图,过点 BG。
关于“一线三垂直” 模型及其在平面几何中的应用(二)“一线三垂直”的性质:1,模型中必定存在至少两个三角形相似,三对等角,三对成比例的边长;2,当模型中有一组对应边长相等时,则模型中必定存在全等三角形。
【例3】如图,在△ ABC 中,AB=AC ,∠ BAC=90o ,分别过B,C 向过 A 点的直线作垂线,垂足分别为E,F。
关于“一线三垂直”模型及其在平面几何中的应用“一线三垂直”模型是“一线三等角”模型的特殊情况,(关于“一线三等角”模型详见比例与相似高级教程(六):相似三角形的“一线三等角”模型),即三个等角角度为90º,于是有三组边相互垂直,所以称为“一线三垂直”模型。
“一线三垂直”的性质:1,模型中必定存在至少两个三角形相似,三对等角,三对成比例的边长;2,当模型中有一组对应边长相等时,则模型中必定存在全等三角形。
“一线三垂直”模型在平面几何中有着及其重要的地位,常出现的图例有以下几种:其中,在“变形2”模型下,根据相似原理,推理出了著名的“射影定理”这里主要讨论有一对对应边相等的情况。
【例1】如图,在等腰直角三角形ABC中,∠ACB=Rt∠,AC=BC,AE⊥CE于点E,BD⊥CE于点D,AE=5cm,BD=2cm,则DE的长为多少?【提示】根据“一线三垂直”模型的性质,△ACE≌△CBD,于是CD=AE=5cm,CE=BD=2cm,DE=5-2=3(cm)【例2】如图,在△ABC中,CA=CB,点D 为BC中点,CE⊥AD于点E,交AB于点F,连接DF。
求证:AD=CF+DF.【解析】此题乍一看起来和【例1】相同,却不能照搬照抄。
从要证明的结论来看,需要把AD这条线段“转化”到直线CF上。
如图,过点B作BG⊥CB,交CF的延长线于点G。
则易证△ACD≌△CBG,于是AD=CG=CF+FG;BG=CD=BD,BF=BF,∠DBF=∠GBF=45º,故△BDF≌△BGF,于是FD=FG,所以AD=CF+DF。
关于“一线三垂直”模型及其在平面几何中的应用(二)“一线三垂直”的性质:1,模型中必定存在至少两个三角形相似,三对等角,三对成比例的边长;2,当模型中有一组对应边长相等时,则模型中必定存在全等三角形。
【例3】如图,在△ABC中,AB=AC,∠BAC=90º,分别过B,C向过A点的直线作垂线,垂足分别为E,F。