【四清导航】七年级数学下册 第10章 相交线平行线(2)18页

初一七年级下册数学知识点：相交线与平行线初一（七年级）下册数学知识点：相交线与平行线平行线与相交线是初一数学下学期学习的第二章内容，主要讲述了相交线、平行线及其判定、平行线的性质等，通过对本篇的学习，相信同学们会更进一步的了解在平面内不重合的两条相交与平行的两种位置的关系，运用平移设计一些优美的图案。

以下是小编带来的初一(七年级)下册数学知识点：相交线与平行线，欢迎阅读。

初一七年级下册数学知识点：相交线与平行线1一、目标与要求1.理解对顶角和邻补角的概念，能在图形中辨认;2.掌握对顶角相等的性质和它的推证过程;3.通过在图形中辨认对顶角和邻补角，培养学生的识图能力。

二、重点在较复杂的图形中准确辨认对顶角和邻补角;两条直线互相垂直的概念、性质和画法;同位角、内错角、同旁内角的概念与识别。

三、难点在较复杂的图形中准确辨认对顶角和邻补角;对点到直线的距离的概念的理解;对平行线本质属性的理解，用几何语言描述图形的性质;能区分平行线的性质和判定，平行线的性质与判定的混合应用。

四、知识点、概念总结1.邻补角：两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角是邻补角。

2.对顶角：一个角的两边分别是另一个叫的两边的反向延长线，像这样的两个角互为对顶角。

3.对顶角和邻补角的关系4.垂直：两条直线、两个平面相交，或一条直线与一个平面相交，如果交角成直角，叫做互相垂直。

5.垂线：两条直线相交成直角时，叫做互相垂直，其中一条叫做另一条的垂线。

6.垂足：如果两直线的夹角为直角，那么就说这两条直线互相垂直，它们的交点叫做垂足。

7.垂线性质(1)在同一平面内，过一点有且只有一条直线与已知直线垂直。

(2)连接直线外一点与直线上各点的所有线段中，垂线段最短。

简单说成：垂线段最短。

(3)点到直线的距离：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。

8.同位角、内错角、同旁内角：同位角：∠1与∠5像这样具有相同位置关系的一对角叫做同位角。

第一讲两条直线的位置关系知识点一：相交线、平行线的概念C1）相交线平行定义：若两条直线只有一个公共点，我们称这两条直线为相交线（2）平行线定义:在同一平面内，不相交的两条直线叫做平行线C3）两套宜线的位置关系：在同…平面内，两条直线的位置关系有相交和平行两种（4）两条直线是指不重合的两条直线注意：1、两条直线在同…平面内2、我们有时说两条射线或线段平行，实际上是指它们所在的直线平行知识点二：关于对顶角的定义和性质定义对顶角：像这样宜线与宜线％相交于。

Z1与/2有公共顶点，它们的两边互为反向延长线, 这样的两个角叫做对顶角.'两条直线相交注意：对顶角的判断条件：有公共顶点无公共边另外，从对顶角的定义还可知：对顶角总是成对出现的，它们是互为对顶角；一个角的对顶角只有一个。

性质同角或等角的对顶角相等。

一般题型下列说法中，正确的是（）.A.有公共顶点，并且相等的角是对顶角B.如果两个角不相等，那么它们•定不是对顶角C.如果两个角相等，那么这两个角是对顶角D.互,补的两个角不可能是对顶角知识点三：互为余角、互为补角的概念及其性质 定义：互为余角：如果两个角的和是直角，则这两个角互为余角.互为补角：如果两个角的和是平角，则这两个角互为补角钝角没有余角 注意：互为余角、互为补角只与角的度数有关，与角的位置无关.性质同角或等角的余角相等，同角或等角的补角相等的补角的余角是.2若匕1与/2互余，Z3和Z2互补，且£3=120°,那么匕1=.如果Zl+Z2=90 °, Z2+Z3=90 °,则匕1与匕3的关系为—，其理由是一如果Zl+Z2=180 °, Z2+Z3=180 °,则与Z3的关系为 ________________ ,其理由是一 经典题型1、已知互余两个角的差是30°,则这两个角的度数分别.练习：1.已知一个角的补角是这个角的余角的3倍，求这个角.2、已知一个角的余角比它的补角的1/4还少12°,求这个角。

相交线与平行线一、目标与要求1.理解对顶角和邻补角的概念，能在图形中辨认;2.掌握对顶角相等的性质和它的推证过程;3.通过在图形中辨认对顶角和邻补角，培养学生的识图能力。

二、重点在较复杂的图形中准确辨认对顶角和邻补角;两条直线互相垂直的概念、性质和画法;同位角、内错角、同旁内角的概念与识别。

三、难点在较复杂的图形中准确辨认对顶角和邻补角;对点到直线的距离的概念的理解;对平行线本质属性的理解，用几何语言描述图形的性质;能区分平行线的性质和判定，平行线的性质与判定的混合应用。

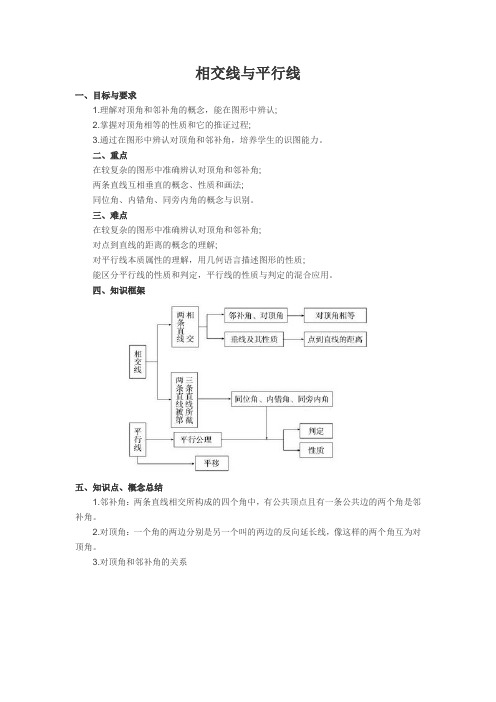
四、知识框架五、知识点、概念总结1.邻补角：两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角是邻补角。

2.对顶角：一个角的两边分别是另一个叫的两边的反向延长线，像这样的两个角互为对顶角。

3.对顶角和邻补角的关系4.垂直：两条直线、两个平面相交，或一条直线与一个平面相交，如果交角成直角，叫做互相垂直。

5.垂线：两条直线相交成直角时，叫做互相垂直，其中一条叫做另一条的垂线。

6.垂足：如果两直线的夹角为直角，那么就说这两条直线互相垂直，它们的交点叫做垂足。

7.垂线性质(1)在同一平面内，过一点有且只有一条直线与已知直线垂直。

(2)连接直线外一点与直线上各点的所有线段中，垂线段最短。

简单说成：垂线段最短。

(3)点到直线的距离：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。

8.同位角、内错角、同旁内角：同位角：∠1与∠5像这样具有相同位置关系的一对角叫做同位角。

内错角：∠2与∠6像这样的一对角叫做内错角。

同旁内角：∠2与∠5像这样的一对角叫做同旁内角。

9.平行：在平面上两条直线、空间的两个平面或空间的一条直线与一平面之间没有任何公共点时，称它们平行。

10.平行线：在同一平面内，不相交的两条直线叫做平行线。

11.命题：判断一件事情的语句叫命题。

12.真命题：正确的命题，即如果命题的题设成立，那么结论一定成立。

13.假命题：条件和结果相矛盾的命题是假命题。

人教版初中数学七年级下 相交线和平行线知识点总结本章使学生了解在平面内不重合的两条直线相交与平行的两种位置关系，研究了两条直线相交时的形成的角的特征，两条直线互相垂直所具有的特性，两条直线平行的长期共存条件和它所有的特征以及有关图形平移变换的性质，利用平移设计一些优美的图案.。

重点：垂线和它的性质,平行线的判定方法和它的性质，平移和它的性质，以及这些的组织运用.5.1 相交线1、邻补角与对顶角两直线相交所成的四个角中存在几种不同关系的角，它们的概念及性质如下表：图形顶点边的关系大小关系 对顶角12∠1 与∠2有公共顶点∠1 的两边与∠2 的两边互为反向延长线对顶角相等即∠1=∠2邻补角43∠3 与∠4有公共顶点∠3 与∠4 有一条边公共，另一边 互为反向延长线。

∠3+∠4=180°⑵如果∠α 与∠β 是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α 与∠β 不一定是对顶角⑶如果∠α 与∠β 互为邻补角，则一定有∠α+∠β=180°；反之如果∠α+∠β=180°，则∠α 与∠β 不一定是邻补角。

⑶两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个。

2、垂线⑴定义，当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

第 1 页共 7 页• PA OB符号语言记作： CAO如图所示：AB ⊥CD ，垂足为 OBD⑵垂线性质 1：过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)⑶垂线性质 2：连接直线外一点与直线上各点的所有线段中，垂线段最短。

简称：垂线段最短。

3、垂线的画法：⑴过直线上一点画已知直线的垂线；⑵过直线外一点画已知直线的垂线。

注意：①画一条线段或射线的垂线，就是画它们所在直线的垂线；②过一点作线段的垂线，垂足可在线段上，也可以在线段的延长线上。