平面光弹性实验

光弹性测试方法实验一．实验目的1. 了解光弹性仪器各部分名称和作用，掌握光弹性仪器的使用方法；2. 观察光弹性模型受力后在偏振光场中的光学效应，加深对典型模型受力后全场应力分布情况的了解：3. 观察等差线和等倾线，学会判别等差线和等倾线。

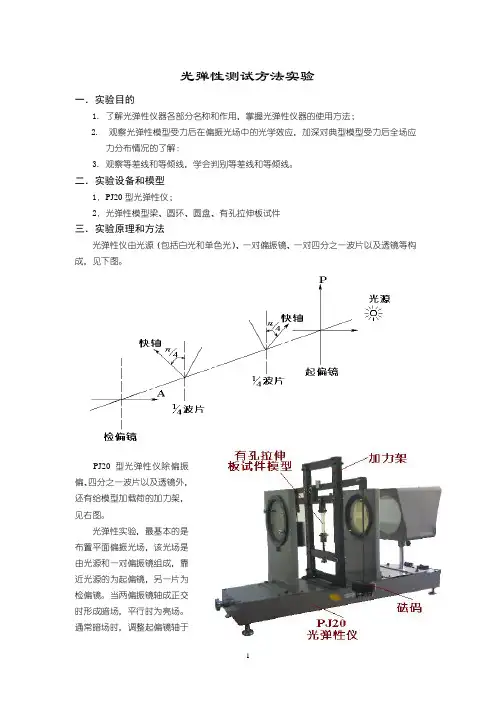
二．实验设备和模型1．PJ20型光弹性仪；2．光弹性模型梁、圆环、圆盘、有孔拉伸板试件三．实验原理和方法光弹性仪由光源（包括白光和单色光）、一对偏振镜、一对四分之一波片以及透镜等构成，见下图。

PJ20型光弹性仪除偏振偏、四分之一波片以及透镜外，还有给模型加载荷的加力架，见右图。

光弹性实验，最基本的是布置平面偏振光场，该光场是由光源和一对偏振镜组成，靠近光源的为起偏镜，另一片为检偏镜。

当两偏振镜轴成正交时形成暗场，平行时为亮场。

通常暗场时，调整起偏镜轴于垂直方向，检偏镜轴为水平方向。

在正交平面偏振光场中，由暂时双折射材料制成的模型受力后，使入射到模型的平面偏振光分解为沿各点主应力方向振动的两列平面偏振光，且其传播速度不同，通过模型后，产生光程差Δ，此光程差与模型厚度h 及主应力差（σ1 - σ2）成正比()21σσ-=∆Ch （1）式中C 为应力光学系数，此式即为平面应力-光学定律，当光程差 Δ为光波波长 λ 的整数倍时，即 Δ=N λ （N=0，1，2 …） （2）产生消光干涉，呈现暗点，同时满足光程差为同一整数倍波长的诸点形成黑色条纹，称为等差线。

由（1）、（2）两式可得hNf =-21σσ （3） 式中f=λ/C 称为模型材料条纹值。

由此可知，等差线上各点主应力差相同，对应于不同的N 值则有0级、1级、2级 …… 等差线。

在模型内凡主应力方向与偏振镜轴重合的点，亦形成一条黑色干涉条纹，称为等倾线。

由等倾线可以确定各点的主应力方向。

当两偏振轴分别为垂直和水平放置时，对应的为零度等倾线。

此时若再将偏振镜轴同步反时针方向旋转100，200… 就得到100，200… 的等倾线，其上各点主应力方向与垂直或水平线成100，200… 夹角。

光弹性实验报告一、 实验目的1. 了解光弹性仪各部分的名称和作用，掌握光弹性仪的使用方法。

2. 观察光弹性模型受力后在偏振光场中的光学效应。

3. 掌握平面偏正光场和圆偏振光场的形成原理，和调整镜片（起偏镜、检偏镜、1/4波片）的方法。

4. 通过圆盘对径受压测量材料条纹级数f ，并通过实验求出两端受压方片中心截面上的应力。

5. 用理论公式计算出方片中心截面上的应力，并与实验得出的数据相比对，判断实验数据的准确性。

二、 实验原理和方法首先引入偏振光的概念，如光波在垂直于传播方向的平面内只在某一个方向上振动，且光波沿传播方向上所有点的振动均在同一个平面内，则此种光波称为平面偏振光。

双折射：当光波入射到各向异性的晶体如方解石、云母等时，一般会分解为两束折射光线，这种现象称为双折射。

从一块双折射晶体上，平行于其光轴方向切出一片薄片，将一束平面偏振光垂直入射到这薄片上，光波即被分解为两束振动方向互相垂直的平面偏振光，其中一束比另一束较快地通过晶体。

于是，射出薄片时，两束光波产生了一个相位差。

这两束振动方向互相垂直的平面偏振光，其传播方向一致，频率相等，而振幅可以改变。

设这两束平面偏振光为：11sin()u a t ω= （1）22sin()u a t ωφ=+ （2）式中 1a 2a —振幅φ—两束光波的相位差将上述两方程（1）（2）合并，消去时间t ，即得到光路上一点的合成光矢量末端的运动轨迹方程式,此方程式在一般的情况下是一个椭圆方程，如果12a a a ==，2πφ=，则方程式成为圆的方程：22212u u a += （3）光路上任一点合成光矢量末端轨迹符合此方程的偏振光称为圆偏振光，在光路各点上，合成光矢量末端的轨迹是一条螺旋线。

因此要产生圆偏振光，必须有两束振动平面互相垂直的平面偏振光，并且频率相同；振幅相等；相位差为π/2。

如平面偏振光入射到具有双折射特性的薄片上时，将分解为振动方向互相垂直的两束平面偏振光。

光弹性实验报告一、实验目的光弹性实验是一种用于测量材料内部应力分布的实验方法。

本次实验的主要目的是通过光弹性实验技术，观察和分析受力模型在不同载荷条件下的等差线和等倾线图案，从而确定模型内部的应力分布情况，并验证理论计算结果。

二、实验原理光弹性现象是指某些透明材料在承受载荷时，会产生暂时的双折射现象。

当一束偏振光通过受力的光弹性材料时，其偏振方向会发生改变，从而产生干涉条纹。

这些干涉条纹反映了材料内部的应力分布情况。

等差线是指光程差相等的点的轨迹，它与主应力差成正比。

等倾线则是指主应力方向相同的点的连线。

通过观察和分析等差线和等倾线的图案，可以计算出材料内部各点的应力大小和方向。

三、实验设备和材料1、光弹性实验仪：包括光源、偏振片、分析片、加载装置等。

2、模型材料：环氧树脂或有机玻璃等光弹性材料制成的模型。

3、量具：游标卡尺、千分尺等。

四、实验步骤1、模型制备选用合适的光弹性材料，根据实验要求制作模型。

确保模型的尺寸精度和表面质量，以减少实验误差。

2、仪器调试打开光源，调整偏振片和分析片的角度，使视场呈现暗背景。

检查加载装置的工作性能，确保加载平稳、准确。

3、模型安装将模型安装在加载装置上，注意安装位置和方向的准确性。

4、加载观测逐渐施加载荷，观察等差线和等倾线的形成和变化。

记录不同载荷下的干涉条纹图案。

5、数据测量使用量具测量模型的尺寸和加载力的大小。

记录等差线和等倾线的级数和角度等数据。

6、实验结束缓慢卸载，关闭实验仪器。

五、实验结果与分析1、等差线图案分析在不同载荷下，等差线的分布和密度发生了明显变化。

随着载荷的增加，等差线的级数增多，表明主应力差增大。

通过对等差线的分析，可以定性地了解模型内部应力集中的区域。

2、等倾线图案分析等倾线的分布反映了主应力的方向。

在模型的不同部位，主应力方向有所不同。

通过测量等倾线的角度，可以计算出主应力的方向。

3、应力计算根据等差线和等倾线的测量数据，结合光弹性实验的基本理论和计算公式，可以计算出模型内部各点的应力大小和方向。

第1篇一、实验目的1. 了解平面光弹性实验的基本原理和方法。

2. 学习使用光弹性实验装置，观察和记录应力光图。

3. 通过实验验证光弹性原理在应力分析中的应用。

二、实验原理光弹性实验是一种利用光学原理研究材料内部应力的方法。

其基本原理是：当光通过具有应力状态的透明材料时，光线的传播方向会发生改变，这种现象称为光弹效应。

通过观察和分析光弹效应，可以推断出材料内部的应力分布情况。

三、实验仪器与材料1. 实验仪器：- 光弹性实验装置（包括光源、显微镜、照相机等）- 模型材料（透明塑料或玻璃）- 标准模型（如拉伸、压缩、弯曲等）2. 实验材料：- 模型材料：透明塑料板或玻璃板- 荧光染料：用于增强应力光图的可视性四、实验步骤1. 准备实验材料，将模型材料切割成所需形状和尺寸。

2. 在模型材料上涂上荧光染料，增加应力光图的可视性。

3. 将涂有染料的模型材料放置在实验装置中，调整光源和显微镜的位置，使光线能够透过模型材料。

4. 开启光源，调整显微镜，观察并记录应力光图。

5. 根据应力光图，分析模型内部的应力分布情况。

6. 对比标准模型，验证实验结果的准确性。

五、实验结果与分析1. 实验过程中，观察到模型材料在不同应力状态下的应力光图。

2. 通过分析应力光图，发现模型材料在拉伸、压缩、弯曲等应力状态下的应力分布情况。

3. 对比标准模型，实验结果与理论预期基本一致，验证了光弹性原理在应力分析中的应用。

六、实验结论1. 光弹性实验是一种有效的研究材料内部应力的方法。

2. 通过观察和分析应力光图，可以直观地了解材料内部的应力分布情况。

3. 光弹性实验在工程实践中具有重要的应用价值。

七、实验注意事项1. 实验过程中，注意安全，避免受伤。

2. 调整光源和显微镜时，保持操作稳定，避免光线晃动。

3. 实验结束后，清理实验场地，回收实验材料。

八、实验总结本次平面光弹性实验，使我们了解了光弹性原理及其在应力分析中的应用。

通过实验，掌握了使用光弹性实验装置的方法，提高了观察和分析应力光图的能力。

实验4 平面光弹性原理——等倾线的测绘和等差线材料条纹级数的测定一、实验目的1、掌握光弹仪的使用，加深认识有应力模型在圆偏振光的暗场和明场中，双折射效应及其力学意义。

2、掌握等倾线的特点。

观察单色光和白光下的等差线，总结当载荷变化时特性点(奇点、各向同性点、源点、汇点)附近条纹变化的规律。

3、观察等差线的特点，初步学会条纹级数的确定方法。

掌握用旋转检偏镜测量非整数级条纹级数的方法。

4、学会等差线的描绘方法及用钉压法判别断自由边界应力符号，并加深对其原理及判断条纹增减方法的理解。

二、实验仪器散射式光弹仪（或409-Ⅱ），圆盘、圆环、等截面梁模型及加载附件。

三、实验原理平面光弹性原理；Tardy 补偿法测量非整数级条纹级数；钉压法判断自由边界应力符号。

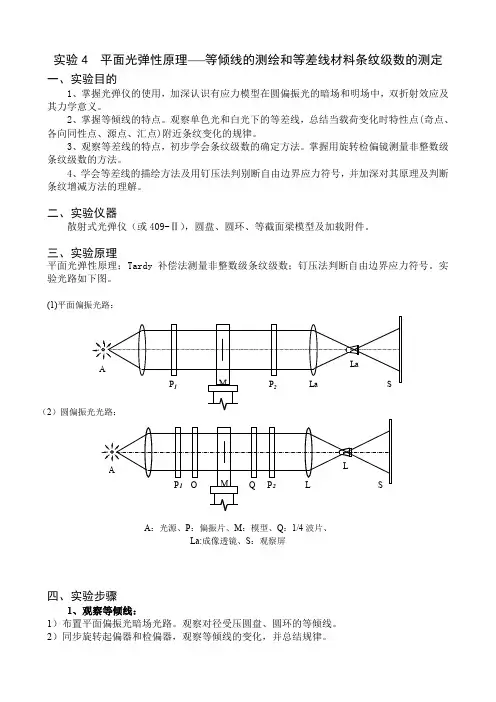
实验光路如下图。

(1)平面偏振光路：A：光源、P：偏振片、M：模型、Q：1/4波片、La:成像透镜、S：观察屏四、实验步骤1、观察等倾线：1）布置平面偏振光暗场光路。

观察对径受压圆盘、圆环的等倾线。

2）同步旋转起偏器和检偏器，观察等倾线的变化，并总结规律。

2、观察等差线：2.1单色光：1）布置圆偏振光暗场光路。

观察对径受压圆盘、圆环的等差线。

2）变动载荷，观察等差线的变化。

试找出模型中的奇点、各向同性点、源点、汇点，总结上述特性点邻域等差线的变化特征。

2.2白光：1）布置圆偏振光暗场光路。

观察对径受压圆盘、圆环的等差线，注意等差线的色序。

2）变动载荷，观察等差线的变化，注意重复消光现象。

3、非整数条纹级次的测定1）开启单色光源，将仪器调节成圆偏振光暗场。

将对径受压圆盘置于光场中央，加载至整数级等差线达5~6 级。

2）再改用明场观察半整数级等差线。

记录注意标明级次。

3）判断条纹级次，使用Tardy 法测量对径受压圆盘中心点的非整数条纹级次。

4、钉压法判定自由边界应力符号将圆盘更换为等截面梁模型及简支梁加载装置，用钉压法判断简支梁上下自由边界应力符号。

记录并绘制等差线的在钉压处的变化。

1. 了解光弹性实验的基本原理和实验方法；2. 学习使用光弹性实验装置进行应力分析；3. 掌握光弹性实验数据处理方法，分析模型的应力分布。

二、实验原理光弹性实验是一种研究物体内部应力分布的方法，其基本原理是利用透明材料在应力作用下产生双折射现象。

通过观察和分析光弹性模型的光学性质变化，可以确定物体内部的应力分布。

实验过程中，将具有双折射现象的透明材料制成研究对象的模型，对模型施加相似载荷，使模型内部产生应力。

此时，模型中的光路发生改变，通过观察和记录模型的光学性质变化，可以分析模型内部的应力分布。

三、实验仪器与材料1. 实验仪器：光弹性实验装置、光源、照相机、量角器等；2. 实验材料：具有双折射现象的透明材料（如硝化纤维素、聚乙烯醇等）。

四、实验步骤1. 准备工作：将透明材料制成研究对象模型，确保模型尺寸符合实验要求；2. 安装模型：将模型放置在实验装置上，调整光源和照相机，使光路通过模型；3. 加载：对模型施加相似载荷，使模型内部产生应力；4. 观察记录：观察模型的光学性质变化，记录光路改变情况；5. 数据处理：对实验数据进行处理，分析模型内部的应力分布。

五、实验结果与分析1. 实验结果：通过实验，观察到了模型在加载过程中的光学性质变化，记录了光路改变情况；2. 数据处理：对实验数据进行处理，得到模型内部的应力分布图；3. 分析：根据应力分布图，分析了模型内部的应力集中区域和应力分布情况。

1. 光弹性实验是一种有效的应力分析方法，可以准确分析模型内部的应力分布；2. 通过光弹性实验，可以了解透明材料在应力作用下的光学性质变化，为材料设计和优化提供依据；3. 实验过程中，应严格按照操作规程进行，确保实验结果的准确性。

七、实验注意事项1. 实验过程中，注意观察模型的光学性质变化，避免光路干扰；2. 加载过程中，注意控制加载速度，防止模型损坏；3. 实验数据应准确记录，以便后续分析。

八、实验总结本次光弹性实验，使我们对光弹性实验的基本原理和实验方法有了更深入的了解。

光弹性实验总结报告光弹性实验总结报告光弹性实验是一种基于光的材料性能测试方法，通过测量材料在光作用下的力学响应来研究材料的弹性性质。

在本次实验中，我们使用了一台光弹性仪，对不同材料进行了测试，并对实验结果进行了分析与总结。

首先，我们选择了五种常见材料（金属、塑料、橡胶、木材和陶瓷）作为实验样本，确定了它们的几何形状和尺寸，并在实验仪器中安装调整好样品。

然后，我们使用了一束激光照射到样品表面，在测力传感器的作用下，实时记录样品的位移和力。

在实验过程中，我们发现不同材料在光照下会呈现出不同的弹性行为。

金属材料在受到光照射后表现出较小的变形和较大的弹性恢复，这是因为金属具有较高的弹性模量和强度。

相比之下，塑料和橡胶材料在光照下会有较大的变形，并且较低的弹性恢复，这是因为它们相对较低的弹性模量和强度。

此外，我们还观察到木材和陶瓷材料在光照射下的行为与金属、塑料和橡胶材料有较大的差异。

木材在受光作用下表现出较小的变形和较大的弹性恢复，这是由于木材具有纤维状结构和较高的纤维间键合强度。

陶瓷材料在光照下则显示出较大的变形和较低的弹性恢复，这是因为陶瓷的结构相对松散且易碎，容易发生永久性变形。

通过对实验结果的分析，我们可以得出结论：光弹性实验是一种有效的材料性能测试方法，可以用于研究不同材料的弹性性质。

不同材料在光照下会呈现出不同的弹性行为，这与材料的组成、结构和强度有关。

金属材料具有较高的弹性模量和强度，而塑料和橡胶材料则具有较低的弹性模量和强度。

木材具有纤维状结构和较高的纤维间键合强度，因此在光照下的弹性行为与金属、塑料和橡胶材料有所不同。

陶瓷材料的结构相对松散且易碎，容易发生永久性变形。

最后，我们还需要指出本次实验中存在的一些限制和改进方向。

由于实验样品的选择有限，我们只能对几种常见材料进行测试，难以得到全面的结果。

在日后的实验中，我们可以选择更多不同类型的材料进行测试，以提高研究的广度和深度。

此外，在实验中还需要注意样品的几何形状和尺寸的选择，以及光照的强度和方向的控制，以确保实验结果的准确性和可靠性。

光弹性应力测试实验报告指导教师：王美芹学院：班级：学号：平行平面偏振场亮纹的条件。

然而，等倾线和等差线在一个图像上显示，难免会使图像不清晰，为了改进实验，我们在实验中把平面偏振场改为圆偏振场，这样就可以得到清晰的等倾线，它与平面偏振场的区别是在装置的模型两侧分别加了一个四分之一波片，当然了，也可以通过快速旋转正交偏振轴，快到应力模型上不同度数等倾线的取代过程用肉眼分辨不出来来消除等倾线的影响。

应力模型所使用的仪器为偏光弹性仪，由光源(包括单色光源和白光光源)、一对偏振镜、一对四分之一波片以及透镜和屏幕等组成，其装置简图1。

图1 光弹性仪装置简图S—光源L—透镜 P—起偏镜M—四分之一波片A—检偏镜O—试件I—屏幕光弹性实验中最基本的装置是平面偏振光装置，它主要由光源和一对偏振镜组成，靠近光源的一块称为起偏镜，另一块称为检偏镜。

当两偏振镜轴正交时开成暗场，通常调整一偏振镜轴为竖直方向，另一为水平方向。

当两偏振镜轴互相平行时，则呈亮场。

M是四分之一波片，若把四分之一波片的快慢轴调整到与偏振片的偏振轴成45o的位置，就可以得到圆偏振光场。

将一个平面受力模型置于平面偏振光场中，入射光矢量E将通过偏振片、模型双折射片和分析片。

光波强度变为I：αϕ2sin2sin222AI=A为常数，α为模型内主应力方向与偏振轴的夹角，ϕ为模型双折射片产生的滞后量。

当光程差为光波波长λ的整数倍时，即D=Nλ????????N=0，1，2， (3)产生消光干涉，呈现暗场，同时满足光程差为同一整数倍波长的诸点，形成黑线，称为等差线，由式（1）、（2）、（3）可得到12Nf hs s-=（4）其中fCl=称为材料条纹值。

由此可知，等差线上各点的主应力差相同，对应于不同的N值则有0级、1级、2级……等差线。

此外，在模型内凡主应力方向与偏振镜轴重合的点，亦形成一暗黑干涉条纹，称为等倾线，等倾线上各点的主应力方向相同，由等倾线可以确定各点的主应力方向。

平面光弹性实验一：实验目的（1）学会绘制等倾线图。

（2）用剪应力差法计算标准模型中某一截面上的应力分布。

二：实验步骤（1）安装好数码光弹仪。

（2）调整好光弹仪各镜轴位置，使之成为正交平面偏振布置。

（3）调整加载架，安装标准试件。

（4）按一定角度间隔小心旋转加载架，观察等倾线图。

（5）绘制等倾线图，安装标准试件。

（6）调整光弹仪各镜轴位置，在双正交圆偏振布置下绘制等差线图，并确定条纹级数。

三：数据分析1：绘制剪应力图。

第一步先跟据不同角度拍摄的图片，帮等倾线画出来。

由于对径受压圆环对称轴是两条等倾线，我选这两条等倾线为坐标轴，我采取的方式是将在白光照射时应力很小时的图片都放在ps中，将所有的图片都旋转到同一个角度（由于做实验的时候模型在旋转），之后根据不同图片等倾线直接绘制等倾线图。

2：根据剪应力差法计算一截面上的应力分布。

在圆偏振布置红色光线照射下的图片上选取线OK作为要计算的截面，在OK 上等距的选取六个等分点从左到右分别为0，1，2，3，4，5，6填入下面剪应力差法计算表格第一列，再选取俩辅助截面AB，CD，与OK的距离都是dy/2。

其中dx/dy=2，且将AB，CD也5等分，如下图所示。

有上面等差线和等倾线条纹图，测量OK，AB，CD截面上各分点的等差线条纹级数N和等倾线角度θ。

不过θ是σ1与x轴的夹角还是σ2与x轴的夹角还是待定，不过由于竖直的等倾线上点θ=0.水平θ=90，则很容易判断θ的大小。

τxy=Nfsin2θ/2h这里f是需要通过计算得到。

Δσ=σ1-σ2=Nf/h，其中圆盘中心的的应力为Δσ=σ1-σ2=8P/（πDh）则f=8P/（πDN），其中N=3.2（红光入射），P=，D=50mm，则f=25000 N/m 通过上面公式就可以计算截面和参考面的τxy。

之后就是计算σx 和σy。

根据（σx）i=（σx）i-1-Δτxy|ii-1Δx/Δy可以算出截面每一点的σx，之后再根据σy =σx-Nfcos2θ/h则σy可以算得四：误差分析本实验由于测量精度不是很高，导致实验数据误差可能很大。

光弹应力测试实验一．实验原理：1、暂时双折射：有些各向同性的透明非晶体材料在自然状态时不会产生双折射，但是当其受到载荷作用而有应力时，产生双折射现象，当载荷卸去时，双折射现象也消失，这种现象称为暂时双折射，也称为光弹性效应。

光弹实验正是应用这种暂时双折射现象。

2、当一束平面偏振光Ep 垂直入射平面应力模型时，光波将沿模型上入射点的两个主应力、方向分解成两列平面偏振光。

这两束光在模型内的传播速度不同，所以通过模型后就产生光程差R 。

光程差R 与该点的主应力差和模型厚度d 呈正比，即或相位差为，式中，c 为模型材料的相对应力光学常数。

由此表明：平面偏振光沿模型上任一点两主应力方向分解的两平面偏振光，在透过模型之后产生的相对光程差或者相对相对位相差与该点的主应力差和模型厚度呈正比。

这称为平面应力——光学定律。

1σ2σ()12-σσ()12R=cd -σσα()122=-πασσλ这样，把一个求主应力差的问题转变为一个求光程差或者位相差的问题。

利用光弹性仪来测定光程差的大小然后根据应力——光学公式确定主应力差值，这就是光弹实验的理论基础。

实验原理图如下：二.实验过程1. 打开激光器，激光束打到分光镜有膜一面（中间的一块）；2. 在模型后20cm左右位置放置白屏，记录位置；3. 调节反光镜，使物光光束透过模型中心，打到白屏上，调节参考光光路反光镜，使参考光光点和物光光点重合；4. 测量两路光程，要做到差距在1cm之内；5. 加上准直镜，为保证激光束垂直通过其光心，调节其位置，使白屏上光点重合，并且使反射光沿原路返回；6. 加扩束镜，撤掉白屏，这时候在墙壁上可以发现一个亮斑。

保证其亮斑中心与未加扩束镜时的亮斑中心重合，然后移动扩束镜，使其亮斑大小与准直镜通光孔径大致相同，并且亮斑均匀；7. 加偏振片&1/4波片，调节角度成45°，加上毛玻璃片；8. 找到两路光重叠的位置，标记；9. 遮住激光束，在黑暗中固定好全息干板。

光弹性效应实验报告实验原理：1. 光弹性效应：有些光学介质在自然状态下没有双折射性质，但当受到机械力作用时，出现双折射现象，应力解除后现象随之消失，这种现象称为光弹性效应。

把具有明显光弹性效应的物质称为光敏物质，其他称为非光敏物质。

在实际应用中，可以用光敏物质做成与待分析部件相似的模型，按部件实际受力情况施加相应的应力。

模型的各受力点产生相应的双折射，即o光与e光折射率n o与n e不同，各点折射率差与改点内应力成正比，即n o-n e=kςK为常数。

利用此原理制成的仪器称为光弹仪。

2.全息光弹法全息光弹法是利用全息干涉原理研究光弹性效应的技术。

光路图如图4-1-1在一个全息照相用的防震台上，让激光束经分束镜分为两束。

一束经扩束镜，准光镜成为平行光，再通过偏振片和四分之一波片成为圆偏振光，经毛玻璃散射后照射待测模型，透过模型投射于全息干板上，这束光称为物光；另一束光经另一套扩束镜，准光镜，偏振片和四分之一波片，成为一束圆偏振光的平行光束，直接投射于全息干板上。

物光与参考光须同时左旋或右旋的圆偏振光。

在模型未加外力时，让物光和参考光同时投射于全息干板上做第一次曝光，记录一次全息条纹；然后给模型加上适当应力，在做第二次曝光。

经两次曝光记录了两套干涉条纹的全息干板显影，定影后，成为全息图。

放回拍摄的位置，撤去实验模型，遮掉物光，以参考光束照射全息图。

迎着原物光方向看，可看到原模型位置有一个所用实验模型的立体虚像，透过望远镜可看到虚像中有明暗相间的干涉条纹。

以ς1表示模型受力最大方向的应力，ς2表示受力最小方向的应力，称ς1与ς2为主应力。

由于沿一个干涉条纹各点有相同的主应力和（ς1+ς2），称此条纹为等和线。

二次曝光法适用于非光敏物质，用于观察等和线。

一次曝光法光路同上，只是在模型未加外力时不曝光，仅在给模型加好外力后作一次曝光，只记录一次全息条纹。

显影定影后放回原位用参考光照明，可用望远镜在模型虚像中看到另一组干涉条纹。