- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Yn n1kn1Xk P
11
二、几个常用的大数定律
1、切比雪夫大数定律
设随机变量序列X1,X2,…,Xn,…相互独立,每一个随 机变量都有相同的数学期望E(Xk)=μ和方差D(X1)=σ2,
则任意正数,
limP n
1n nk1
Xk
1
即
1
n
n k 1
Xk
P
12
证明 因为X1,X2,…,Xn,…相互独立,
1
n
n k 1
Xk
P
注:
E(1 nkn 1Xk)1 nkn 1E(Xk)
8
例: 设随机变量 X1, X 2 , , X n , 相互独立,且有如 下表的分布律,问:对随机变量 X1, X 2 , , X n , 可 否使用大数定理?
Xi 2
0
pi
1 4
1 2
2
(i1,2,,n,)
1 4
解
g (X n , Y n ) P g (a ,b )
4
二、 切比雪夫(Chebyshev)不等式
• 定理(切比雪夫(Chebyshev)不等式):设随机变 量X具有数学期望E(X)=μ,方差D(X)=σ2 ,则对于任 意正数ε,有
P| X|22
PX122
5
证明 (1)设X的概率密度为p(x),则有
Xik
PE(Xik)
16
4.7 中心极限定理
前面我们的讨论中讲过正态分布在随机变量的一切 可能分布中占有特殊地位。在客观世界中,我们遇到 的许多随机现象都是服从或近似服从正态分布的,为 什么大量的随机变量都服从正态分布?
俄国数学家李亚普诺夫(Ляпуров)证明了在某些非 常一般的充分条件下,独立随机变量的和的分布,当 随机变量的个数无限增加时,是趋于正态分布的。
该定理表明:相互独立的随机变量的算数平均值
X
1 n
n
Xi
i1
与数学期望的算数平均值的差在n充分大时是一个无穷小
量,这也意味着在n充分大时,经算术平均后得到的随机
变量 X 的值将比较紧密地聚集在它的数学期望 E ( X )的附
近。
13
2、切比雪夫大数定律的特殊情况
设随机变量序列X1,X2,…,Xn,…相互独立,且具有相 同的数学期望μ和相同的方差σ2,记前n个随机变量的算
不等式求概率 P X 的近似值.
解 当2时
PX2 2 1
22 4 当 3时
PX3 2 1
32 9
7
• 切比雪夫大数定律:设{Xk}是相互独立的随机变 量序列,具有相同的数学期望E(Xk)=μ和方差 D(Xk)=σ2(k=1,2,…),则对于任意给定的ε>0,恒有
lim n P {1 n | kn 1Xk |}1
2
5.1 大数定理
一、依概率收敛
定义5.1.1 (依概率收敛)
若对任意的 >0,有 nl im PYnY1
则称随机变量序列{Yn}依概率收敛于Y, 记为
Yn PY
大数定律讨论的就是依概率收敛.
3
依概率收敛(续)
(多变量函数)
设 Xn Pa ,Yn Pb ,又设函数
g(x,y)在点(a,b)连续,则
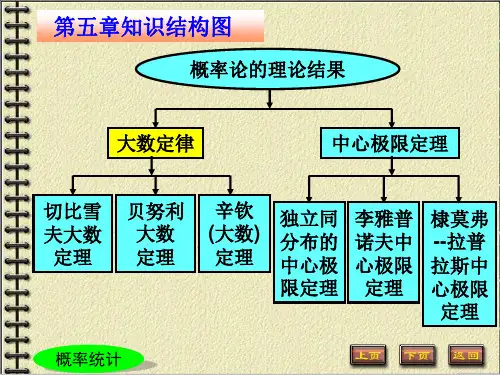
第五章 大数定律及中心极限定理
大数定律 中心极限定理
1
“概率是频率的稳定值”。 前面已经提到,当随机试验的次数无限增大 时,频率总在其概率附近摆动,逼近某一定值。 大数定理就是从理论上说明这一结果。 正态分布是概率论中的一个重要分布,它有 着非常广泛的应用。中心极限定理阐明,原本不 是正态分布的一般随机变量总和的分布,在一定 条件下可以渐近服从正态分布。 这两类定理是概率统计中的基本理论,在概 率统计中具有重要地位。
D 1 nkn 1X k n 1 2kn 1D (X k)n 1 2n cn c E1nkn1Xk1nkn1E(Xk)
由切比P雪1 n夫kn 1不X等k式1 n可kn 1得E(Xk)D 1 nkn 21Xknc2
n l im P1 nkn 1Xk1 nkn 1E(Xk)0
因为 X1, X 2 , , X n ,
相互独立, EX i 0 , E
X
2 i
1
又
DX i
E
X
2 i
EX i
2
1 0
1, i
1,2,
, n,
所以,满足切比雪夫大数定理的条件,可使用大数定理.
9
伯努里大数定律: 设进行n次独立重复试验,事
件A发生的次数为 n A , 每次试验中事件A发生的概 率为p,则对任意的 0, 有:
DnA
P
nA n
p
n pq
2 n2
ln imP
nA n
p
0
15
4、 辛钦大数定律
若{Xk,k=1,2,...}为独立同分布随机变量序列,
EXk=<,k=1,2,…,则
Yn n1kn1Xk P
推论:若{Xi,i=1.2,...}为独立同分布随机变量序列, E(Xik)存在,则
1 n
ni1
limP{| n
nA n
p|}1
证明:设
1
X
i
0
第i次试X i 验事件A发生 第i次试验事件A不发生
则
E (X i) p ,D (X i) p (1 p )
由切比雪夫大数定律
limP{| n
nA n
p|}1
10
辛钦大数定律 若{Xk,k=1,2,...}为独立同分布随机变量序列,
E(Xk)=,k=1,2,…,则
术平均为Yn,
1 n
Yn n i1 X i
Hale Waihona Puke 则随机变量序列Y1,Y2,…,Yn,…依概率收敛于μ,即
Yn P
0 n l im P Y n 0
证明 1ni n1E(Xi)1nn D(Xi)2
ln i m P1 ni n1Xi 1 ni n1E(Xi)ln i P m Y n 0
P{X | |} p(x)dx |
|x|
|x|
x|2 2
p(x)dx
12 (x)2p(x)d x 22
(2)设离散型随机变量X的分布律为P{X=xk}=pk,则有
P {X ||} P {Xxk} |xk|
[xk ]2
2
|xk|
P{Xxk}
1
2
k
[xk
]2pk
2 2
6
例:已知随机变量 X 的数学期望为 E(X)=μ,方 差 D(X ) 2,当 2 和 3 时,试用切比雪夫
切比雪夫大数定律 14
3、贝努里大数定律
设进行n次独立重复试验,每次试验中事件A发生
的概率为p,记nA为n次试验中事件A发生的次数,则
0
ln imP
nA n
p
0
即 nA P p n
证明(由切比雪夫不等式可直接证明)
nA ~B(n,p)
E(nnA)1 nE(nA)1 nnp p
0
D (n n A)n 1 2D (nA)n 1 2npq p nq