当前位置：文档之家 › §3-2 一维双原子链的晶格振动

§3-2 一维双原子链的晶格振动

  • 格式：ppt
  • 大小：136.50 KB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

位势的一维双原子链的晶格振动色散曲线

位势的一维双原子链的晶格振动色散曲线

位势的一维双原子链的晶格振动色散曲线一维双原子链是研究晶格振动的常见模型之一，其可用于解释晶体的声学和光学性质。

在研究晶格振动的过程中，色散曲线是一个重要的参考内容，它描述了晶格振动的频率与波矢之间的关系。

本文将介绍一维双原子链的晶格振动色散曲线的相关内容。

一维双原子链是由两种原子按照ABAB...的周期性排列形成的周期性结构。

为了便于分析，我们假设这两种原子的质量分别为m1和m2，弹性常数分别为k1和k2。

通过应用牛顿定律和胡克定律，可以得到一维双原子链中晶格振动的运动方程。

在固体物理学中，将波的传播方向为x轴，位置为x的原子质点振动的位移为u(x, t)，根据牛顿定律和胡克定律，可以得到一维双原子链的晶格振动的运动方程为：m1∂²u(x, t)/∂t² = k1[u(x+a, t) - u(x, t)] + k2[u(x-a, t) - u(x, t)]m2∂²u(x, t)/∂t² = k2[u(x+a, t) - u(x, t)] + k1[u(x-a, t) - u(x, t)]其中，a为晶格常数，表示相邻原子之间的距离。

通过将位移u(x, t)展开为平面波的形式，可以将上述两个方程变换为光学模式和声学模式的形式，从而得到晶格振动的色散关系。

对于光学模式，位移u(x, t)可以表示为：u(x, t) = A1exp[i(kx-ωt)] + A2exp[-i(kx-ωt)]其中，A1和A2为振幅，k为波矢，ω为角频率。

将该位移代入运动方程中，可以得到：m1ω² = 2k1 - 2k1cos(ka)m2ω² = 2k2 - 2k2cos(ka)并且，根据周期性边界条件，可以得到波矢k满足的条件为：exp(ika) + exp(-ika) = 2cos(ka) = -m2/m1通过解以上方程组，可以得到光学模式的色散关系，即角频率ω与波矢k之间的关系。

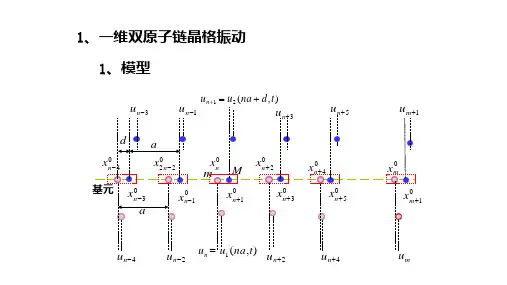
高二物理竞赛一维双原子链晶格振动课件

高二物理竞赛一维双原子链晶格振动课件


色散关系（频率与波矢的关系）
一维单原子链动力学方程的一般解 得到：
l 0, 1, 2,
Gl
表示同一格波，所以可以将 q e的取iN值aqq 限制1在第一N布a里q渊区：2 ,
n 1,2,3, N
l 0,1,2,
当两个原子的振动位相差为2 Aei(qx t )
的整数倍时，两个原子q的振动2位移l相,
m
d 2un dt 2
(un1
un1
2un
)
强行者有志。
胸有凌云志，无高不可攀。 贫困教会贫困者一切。 贫穷是一切艺术职业的母亲。
得到： m 2u eiaqu eiaqu 2u
n
n
n
n
学做任何事得按部就班，急不得。
壮志与毅力是事业的双翼。
立志是事业的大门，工作是登门入室的旅程。 褴褛衣内可藏志。 人若有志，万事可为。 志，气之帅也。
将动力学方程的一般解
un
u(na,t)
i( 2nat )
Ae
Aei(naqt)
人 志无之志所向 趋， ，和 无迷 远途 勿的 届盲 ，人穷一 山样 复。 海不能代限也入;志动之所力向学，无方坚程不摧，。
鸟不展翅膀难高飞。 穷人的孩子早当家。 人之所以异于禽者，唯志而已矣! 志坚者，功名之柱也。登山不以艰险而止，则必臻乎峻岭。
等，晶体原子振动以格波在晶体中传
l 0,1,2
播。
2、相邻间距为d 的两个原子的恢复力系数为
; Na
3、相邻间距为(a-d)的两个原子的恢复力系数为 2
u2 (na, t) 格波圆频率具有中心反演对称性： 若格波波长 比晶体原子间距离大得多，即
由于 q
a
a
晶格振动

晶格振动


例1.求由5个原子组成的一维单原子晶格的振动频率。设原
子质量为m，恢复力常数为(只考虑近邻原子间的相互作用)。
解:设最近邻原子间的恢复力系数为，则:
..
m xn xn xn1 xn xn1
xn Aeitnaq
将试探解代入振动方程得色散关系:
;
m
当 q 0, min 0
由色散关系式可画图如下:
m
2 sin aq
m
2
2π / a π / a
0
π/ a
2π / a
是波矢q的周期性函数,且(-q)= (q)。

m
2 sin aq
m
2
2π a
π a
o
πa
2π a
当 q , q 2π s ( s为 整 数), a
2
2
整数
q 2π s Na
s ( N 1),( N 2),( N 3), ,1, 0,1, 2, , N (共N个值)
2
2
2
2
波矢 q

2π Na
s
也只能取N个不同的值。
晶格振动波矢只能取分立的值
波矢的数目(个数)=晶体原胞的数目
4. 长波极限: q 2π 0
2
aq
sin
m
2
由玻恩---卡门周期性边界条件:
x1 x1 N
eiNaq 1
S为整数
Naq 2π s
q 2π s 5a
πq π
a
a
5<s 5
2
2
5<s 5
2
2
s 2, 1, 0, 1, 2
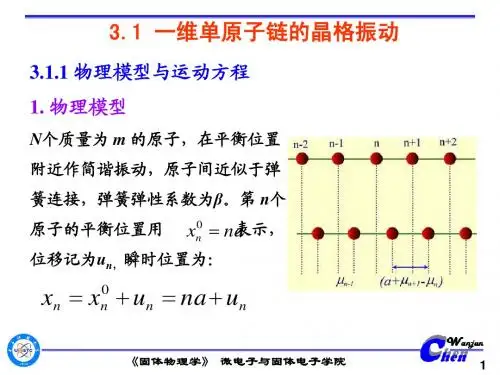
第3章 晶格振动

第3章 晶格振动


《固体物理学》 微电子与固体电子学院
12
3.1 一维单原子链的晶格振动
3. 格波的意义
连续介质波：
x i 2 t
Ae
Ae
i qxt
波矢：q
2

格波： u
n
Ae
i qnat
《固体物理学》 微电子与固体电子学院
13
3.1 一维单原子链的晶格振动
25
3.1 一维单原子链的晶格振动
相邻原子之间的作用力：
f ,
f a
a
K=βa是原子链的伸长模量。 格波传播速度：
c a ，c a a K m m/a
连续介质弹性波的相速度：VElastic K
可见两者相速度相同。因此在长波极限下，对以一维单原
《固体物理学》 微电子与固体电子学院 24
3.1 一维单原子链的晶格振动
2. 长波极限
当q趋近0，即波长很长时：
sin(qa ) qa 2 2
aq m
在长波极限下一维单原子晶格
格波的色散关系和连续介质中 弹性波的色散关系 VElasticq 一致。
《固体物理学》 微电子与固体电子学院
晶体中格波和连续介质波具有完 全类似的形式。一个格波表示的 是所有原子同时做频率为ω的振 动。在简谐近似下，格波是简谐
平面波。
图中的向上箭头代表原子沿X轴 向右振动，向下箭头代表原子沿 X轴向左振动。箭头的长度代表 原子离开平衡位臵位移的大小。
《固体物理学》 微电子与固体电子学院 14
3.1 一维单原子链的晶格振动
格波的波长：
2 q
格波的波矢：q 2 n n 代表沿格波传播方向的单位
一维双原子链晶格振动光学支与声学支频隙宽度

一维双原子链晶格振动光学支与声学支频隙宽度

一维双原子链晶格振动光学支与声学支频隙宽度一维双原子链晶格是一个理想模型，用于研究晶体中原子振动的性质。

它由两种原子按特定顺序排列而成，可以看作是一条由不同类型原子组成的链。

在这个模型中，每个原子可以看作是一个质点，它们在平衡位置附近以简谐振动的方式运动。

在一维情况下，原子只能在链的方向上振动，其振动模式有两种：光学模式和声学模式。

对于一维双原子链晶格，振动可以用简谐振动的方程描述：m₁x₁''(t) + k₁(x₁(t) - x₀(t)) + k₂(x₂(t) - x₁(t)) = 0,m₂x₂''(t) + k₂(x₂(t) - x₁(t)) + k₃(x₃(t) - x₂(t)) = 0,...mₙxₙ''(t) + kₙ(xₙ(t) - xₙ₋₁(t)) + kₙ₊₁(xₙ₊₁(t) - xₙ(t)) = 0,其中，m₁、m₂、...、mₙ分别为原子的质量，k₁、k₂、...、kₙ分别为原子之间的弹性系数，x₁(t)、x₂(t)、...、xₙ(t)分别为原子的位移。

这个方程组可以通过求解本征频率和模位移来描述晶格的振动性质。

根据以上方程，可以得到一维双原子链晶格的频率-波矢关系，即声学支和光学支的频率分布。

在这个关系中，频率由波矢 k 决定，光学支频率通常高于声学支频率。

对于声学支，原子振动是同相的，在低频区域可以近似看作是一组刚性振动模式。

在一维双原子链晶格中，声学支的频率在特定波矢区间内存在频隙，即不存在振动模式。

这个频隙的宽度取决于原子质量、弹性系数和晶格常数等因素。

频隙宽度越大，声学支频率范围限制的越小。

对于光学支，原子振动是异相的，在低频区域振动模式不存在。

光学支的频率范围从声学支频率频隙起始位置开始，直至无穷大。

这个频率范围内存在多个振动模式，频率越高，振动模式的数量越多。

一维双原子链晶格的声学支和光学支频隙宽度是研究材料的重要参数，能够提供有关晶体性质的信息。

晶格振动 (2.双原子模型)

晶格振动 (2.双原子模型)

( 2 M ) B 2 cos( qa ) A 0
2
• 由
2 cos( qa ) B ( 2 m ) A 0
2
• 可得
A B

2 M
2
2 cos( qa )
0
• 因为对光学支 min ( q )
2 m
• 所以振幅之比小于零，这表示相邻不同原子的 振幅方向相反
光学支
LO
LA
离子晶体中长光学波 有特别作用：相对振 动产生电偶极矩，与 电磁波相互作用，导 致强烈的红外光吸收
q
声学支
/a
0
/a

光学支 (2/1/2 M>m
LA LO
(2/m1/2 (2/M1/2
声学支
/a
q
振幅之比——声学支
( 2 M ) B 2 cos( qa ) A 0
2
本征方程
( 2 M ) B 2 cos( qa ) A 0
2
2 cos( qa ) B ( 2 m ) A 0
2
本征方程
2 M
2
2 cos( qa ) 2 m
2
2 cos( qa )
0
(q )
2
( M m ) M Mm
(二）
晶格振动，声子(II)
2、一维双原子链的晶格振动
2、一维双原子链的晶格振动 M
2n-2 平衡时 振动时偏离 平衡位置
d x2n dt
2 2 2
2n-1
2n
2n+1 2n+2
m
a
x2n-1 x2n
3.2二维晶格振动

3.2二维晶格振动

M 2 B eiaq e iaq A 2 B


m 2 Aei[ t ( 2n1)aq ] {Bei[ t ( 2n2)aq] Bei ( t 2naq ) 2 Aei[ t ( 2n1)aq] }
m 2 A e iaq e iaq B 2 A
2mM 2 (aq) m M m M 1 2 mM m M
2mM (aq) 2 mM m M
2 aq m M
v pq
vp 2 a m M



A
(2)相邻原子的振幅之比
(1)当波矢q
2 A
0时, cos(2aq) 1
1 2aq2 则, 2
1 2 2 2 m M m M 2mM cos2aq
mM

A
2 aq, m M
vp
2 a m M
在长波近似的情况下，声学支格波与弹性波的情况类似。
A 0 BA
cos(aq) 0, A
2 2 , 所 以2 m A 0, M
声学支格波，相邻原子都是沿着同一方向振动的。
； q 0, cosaq 1 A 0
AB
长声学波，相邻原子的位移相同，原胞内的不同原子以相 同的振幅和位相作整体运动。因此，可以说，长声学波代表了 原胞质心的运动。 对于光学波:
mA MB 0,
长光学波，原胞的质心保持不动。所以定性地说，长 光学波代表原胞中两个原子的相对振动。
光学波
声学波
光学支格波，相邻原 子振动方向是相反的。
声学支格波，相邻原 子振动方向是相同的。
固体物理基础第3章 晶格振动理论

固体物理基础第3章 晶格振动理论

14
第3章 晶格振动理论
基于如下的物理考虑：首先，晶体的宏观热性质取决于 组成晶体的绝大多数原子的运动状态；其次，晶体边界(表 面)原子的数目远小于晶体内部原子数目，因此对晶体热性 质的影响很小；第三，按照近邻作用近似，边界原子对内部 原子运动状态的影响很小。于是，玻恩-卡曼提出了这样的 周期性边界条件：假定由数目巨大的N个原子组成的一维单 原子链首尾衔接(间距也为a)，构成一个如图3.3所示的半径 很大的圆环，局部范围内原子沿环方向的振动仍然可以看做
2
第3章 晶格振动理论 μn+2，…表示，第n个原子的实际位移为Xn=na+μn，如图 3.1(b)所示。尽管晶格中任一原子都会受到其他(n-1)个原子 的作用，但是这种作用会随着原子间距的增加而快速减小， 这是比较容易理解的，因此，为了使问题进一步简化，可以 进行近邻作用近似，即假定晶格中任一原子只受到其最近邻 原子的作用。这样的话，由于晶格中相邻原子间的相互作用 (化学键)都相同，就可以把一维单原子链想象成N个原子由 完全相同的弹簧连接的情况，如图3.1(c)所示，于是对于第n 个原子，只受到前后两个原子的作用fn-1，fn+1，它们与原子 的相对位移成正比，并且具有相同的弹性系数(或者叫回复 力系数)β。
把这些连续量带入方程(3.1)整理后即可得到：
m 2 ( t2 x ,t) 2 x (x 2 ,t)a 2 2 ( t2 x ,t)0 2 2 x (x 2 ,t)
(3.3)
7
第3章 晶格振动理论
这是数理方程中的波动方程，其中
2 0
程的特解为
a2 m
为波速度，该方
(x,t)Aei(tqx)
这是由2N个方程组成的联立方程组。同样，该方程组 应该具有下列形式的格波解，只是由于P原子和Q原子质量 的不同，其格波解的振幅不同：
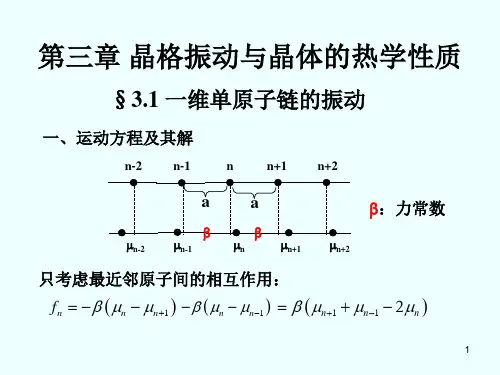
固体物理--第三章 晶格振动ppt课件

固体物理--第三章 晶格振动ppt课件


5
2a
2
q2 q1 a
5
三、周期性边界条件（Born－Karman边界条件）
N+1
12
n
N N+2 N+n
N n
n
Aeit N naq Aeitnaq
eiNaq 1 ei2h 1
q 2 h
Na
h =整数
6
在q轴上，每一个q的取值所占的空间为 2
Na
q的分布密度：
q Na L
子数不守恒。
11
§3.2 一维双原子链的振动
考虑由P、Q两种原子等距相间排列的一维双原子链
一、运动方程及其解
a Mm
{
n-1 n n n+1
只考虑近邻原子间的弹性相互作用
{ 运动方程：
M n n n1 2n
m n n n1 2 n
试 解：
it naq
Ae n
{ Bei
q 0
光波： ＝c0q， c0为光速
对于实际晶体， ＋(0)在1013 ~ 1014Hz，对应于远 红外光范围。离子晶体中光学波的共振可引起对远红外 光在 ＋(0)附近的强烈吸收。
18
2. 声学波（acoustic branch）
n n
M
m
2m
cos
1 2
aqei
12aq
M 2 m2 2Mm cosaq
2 2
L＝Na ——晶体链的长度
简约区中波数q的取值总数 q 2 Na 2
a 2 a
＝N＝晶体链的原胞数
晶格振动格波的总数=N·1 =晶体链的自由度数
7
四、格波的简谐性、声子概念
晶体链的动能：
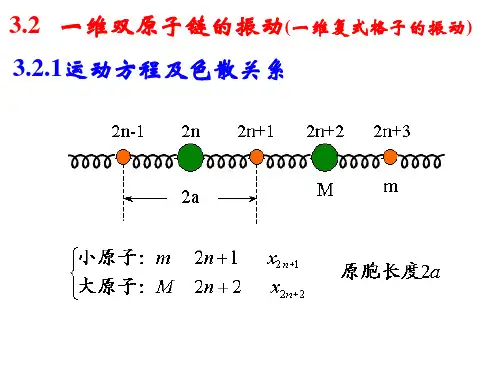
固体物理(第6课)一维双原子链

固体物理(第6课)一维双原子链

这个晶格振动的波动函数只在分立的格点R0处有值。
r i (ωt −kna)
r r R0 (l, m) = Rl + rm
其中k为波矢量，即波传播的方向。在三维情况下， 每个允许的波长，都有两个横波和一个纵波。横波的速 度相同，纵波的速度大于横波，是由于纵向弹性系数大 于横向弹性系数。 上式中j,k是晶格平面波解的参数，其中j代表3na支具 有不同频率ωj(k)的晶格振动波。。 当波矢K在FBZ中取值时，每个K对应3na振动模式， 故格波分为3na支，每一支有自己的色散关系，它们分为 3na –3只光学支和3 只声学支，其中声学支的特点是在 FBZ的中心，谐振频率为零，即 ω（q=0）=0。
返回
光学波可用光波的电磁场激发，即称为光学波。
3. 晶格振动的一般结论*
一维单原子链 一维双原子链 N(1) N(2) 波矢数 模式数 格波支数 N N 1(声) 声 N 2N 2 1:声 声 1:光 光 三维晶体 N(n) N 3nN 3n 3:声 声 3(n-1):光 光
(1)晶格振动的波矢数＝晶体中的原胞数 (2)晶格振动的模式数＝晶体中原子的自由度数 (3)晶格振动的格波支数＝晶体原胞的自由度数
v 2π ⋅ nx v 2π ⋅ ny v 2π ⋅ nz v I+ K k= J+ L L L
v k空间 波矢空间 状态空间
声学波 横波 光学波 2. 声学波 纵波 光学 波
3nN 3nN
TA(transvers e acoustical w ave) TO(transvers e optical w ave) LA(longitudin al acoustical w ) ave LO(longitudin al optical w ave)
一维双原子链晶格振动光学支与声学支频隙宽度

一维双原子链晶格振动光学支与声学支频隙宽度

一维双原子链晶格振动光学支与声学支频隙宽度一维双原子链晶格是指由两种不同原子交替排列而成的一维晶格结构，其中每个原子可以在垂直于链方向上振动。

这种双原子链的振动特性可以通过研究其光学支和声学支的频隙宽度来描述。

在一维双原子链晶格中，存在两种不同的振动模式：光学模式和声学模式。

光学模式是指原子在振动时相互反向移动，而声学模式则是指原子在振动时同向移动。

这两种模式的频率可以通过计算得到，并可以根据频率的不同分为光学支和声学支。

光学支是在高频区域出现的一系列频率，其频率范围内没有振动模式存在。

声学支是在低频区域出现的一系列频率，其频率范围内存在振动模式。

频隙是指光学支和声学支之间的频率范围，即在该范围内不存在振动模式。

针对一维双原子链晶格的光学支和声学支频隙宽度的计算方法可以通过对其方程模型进行求解来获得。

在这个求解过程中，可以使用周期性边界条件来计算结构中的振动模式。

例如，对于一维双原子链晶格振动的光学支，可以使用Bloch 定理来建立方程模型。

Bloch定理是描述周期性结构中电子波函数的一种数学工具，可以用于描述振动模式的波函数。

利用Bloch定理，可以得到一维双原子链晶格的光学支的频率与波矢之间的关系。

对于一维双原子链晶格振动的声学支，可以采用拟合弹簧振子模型来建立方程模型。

在这个模型中，可以假设双原子链中的原子之间的相互作用力恒定，即每个原子与邻近原子之间的弹簧劲度系数相同。

通过求解这个方程模型，可以得到声学支的频率与波矢之间的关系。

通过计算得到一维双原子链晶格振动的光学支和声学支的频率与波矢之间的关系后，可以确定频隙的宽度。

频隙的宽度表示光学支和声学支之间不存在振动模式的频率范围。

频隙宽度的大小取决于晶格的几何结构、原子质量、弹簧劲度系数等因素。

总之，一维双原子链晶格振动的光学支和声学支频隙宽度是通过求解方程模型得到的，并可以通过计算频率与波矢之间的关系来确定。

这些信息对于了解一维双原子链晶格的振动特性以及相关应用具有重要意义。

一维双原子链的晶格振动


22 //N aa N
2020/4/1
注意:
• 这里的N为一维晶格的初基原胞数。每个q对 应两个频率（ωA和ω0），则共有2N组ω,q）， 所以一维双原子链有2N个格波，或说有2N个 简正模式。晶体中任何一原子的运动，为这 2N个格波所确定的谐振动的线性叠加。这时 ，晶体的总自由度数也为2N，推广的结论：
入射红外光波与离子晶体中长光学波的共振 能够引起对入射波的强烈吸收，这是红外光 谱学中一个重要的效应。因为长光学波的这 种特点，所以称ω0 所对应的格波为光学波。 现在来考察一下两种原子的振幅比。把
式（3－23）代入（3－22）可得
A2 A1
2020/4/1
1eiq a 1eiq a
e 2 iqd
§3－2 一维双原子链的晶格振动
一、模型与色散关系
设一维晶体由N个初基原胞组成，每个初基 原胞有二个质量相等的原子，分别用A与B表 示，每个原子和它的左右近邻间距不等，弹 性系数也不等。晶格常数为a 。原子A与其右 侧B原子距离为d，弹性系数为β2 ，与其左侧 B原子的距离为（a-d）弹性系数为β1，为确定 起见，并设d<（a-d），β1<β2。
（3－23）
即有两支ω～q 的色散关系。
当取“－”号时，ω记为ωA，称为声学支 取“＋”号时，ω记为ω0，称为光学支
2020/4/1
2020/4/1
声学支（Acousticbranch）
ωA2=（β1＋β2）/m -(β12＋β22＋2β1β2cosqa)1/2 /m
它具有q=0时，ωA ＝0的特征。 而光学支（Optical branch）格波
2020/4/1
允许的波矢数＝晶体的初基原胞数 格波总数＝晶体振动的总自由度数

第三章 晶格的振动

2 2 m M sin qa 2 1 (m M ){1 [1 ]} 2 mM ( M m) 2 sin 2 qa M m 2 1 sin qa M m

2）对于光频支 1 •当q=0时， 2 2 {( m M ) [m 2 M 2 2m M ] 2 } mM 2 M m 2 Mm
2 2
1 2
2 max
2 min
2
2

,q 0

光频支

2 2 ( ) m 1 2 2 ( ) M
1
2 ,q m 2a
1max
2 ,q M 2a

声频支
1min 0, q 0

2a
0

2a
q
一维复式晶格的色散关系
4. 结果讨论 1）对于声频支 1 •当q=0时， 12 {( m M ) [m 2 M 2 2m M] 2 } 0

2
1 2
分析：对于一维复式格子，可以存在两种不 同的 格波，这两种不同的格波各有自己的色散关系。 声频支：

2 1

mM
{(m M ) [m M 2m M cos(2qa)] }
2 2
1 2
光频支：

2 2
Hale Waihona Puke mM{(m M ) [m M 2m M cos(2qa)] }
mM 其中 为约化质量 mM
•当 q
2a
2 2 时， 2 {( m M ) [ M m]}
mM m
5. 声频支和光频支的振动特点 1）声频支 2 ( 2 m 两种原子的振幅比： 1 ) A 2 cos qaB 0

第三章 晶格振动和晶体的热学性质

第三章晶格振动和晶体的热学性质[引言]晶体中原子、离子实际上不是静止在晶格平衡位置上，而是围绕平衡位置作微振动，称为晶体振动。

对晶体振动的研究是从解释固体的热学性质开始的，最初把晶体中的原子看作是一组相互独立的振子，应用能量均分定理可以说明固体比热容服从杜隆-珀替定律，但与T=0K时的0C=的规律不符。

1906年爱因斯坦提出固体比热容的量子理论，V认为独立谐振子的能量是量子化的，可以得到T=0K时0C=的规律的结论，但与低温V下3C T的实验结果不符。

1912年德拜提出固体的比热容理论，把固体当成连续介质，~V晶格振动的格波看连续介质中的弹性波，得到低温下3~C T的结果。

随后，玻恩及玻V恩学派逐步建立和发展了比较系统的晶格振动理论成为最早发展的固体理论之一。

晶格振动理论不仅可以用来解释固体的热学性质、结构相变等许多物理性质都是极为重要的，是研究固体物理性质的基础。

因为固体是由大量原子组成的，原子又由价电子和离子组成，所以固体实际上是由大量电子和离子组成的多粒子体系。

由于电子之间、电子与离子以及离子之间的相互作用，要严格求解这种复杂的多体问题是不可能的，但注意到电子与离子的质量相差很大，离子的运动速度比电子慢得多，可以近似地把电子的运动与离子运动分开考虑，变成一个在晶格周期场中运动的多电子问题；在考虑离子的运动时，则认为电子能够即时跟上离子位置的变化，变成离子或原子如何围绕平衡位置运动的问题。

这种近似称为绝热近似。

晶格振动理论就是在这个近似的基础上建立的。

本章首先从最简单的一维晶格出发，说明晶格振动的基本性质，然后推广到三维情况，最后讨论晶体的热学性质。

[本章重点]一维单原子链晶格振动，一维双原子链晶格振动，声子，晶格比热的德拜模型，晶格振动的模式密度，N 过程与U 过程§3-1一维单原子链考虑由N 个相同的原子组成的一维晶格，如图3-1-1所示，相邻原子间的平衡距离为a ，第j 原子的平衡位置用x 0j 来表示，它偏离平衡位置的位移用u j 来表示，第j 原子的瞬时位置就可以表示为：j j j u x x +=0………………………………………………(3-1-1) 原子间的相互作用势能设为)(ij x ϕ，如果只考虑晶体中原子间的二体相互作用，则晶体总的相互作用能可表示为：()∑≠=Nji ij x U ϕ21……………………………………………(3-1-2)式中ij ij i j ij u x x x x +=-=0是i 、j 原子的相对距离，i j ij u u u -=是i 、j 两原子的相对位移，在温度不太高时，原子在平衡位置附近作微振动，相邻原子的相对位移要比其平衡距离小得多，可将ϕ展开为：………………(3-1-3)于是有：()∑∑∑≠≠≠+⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫⎝⎛∂∂+=j i ij ij j i ij ijj i ij u x u x x U 202200412121ϕϕϕ……………(3-1-4) 图3-1-1 一维单原子晶格()()()+⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+=+=2220021ij ij ij ijijij ijij u x u x xu x x ϕϕϕϕϕ式中第一项是所有原子处于平衡位置上时的总相互作用能，用U 0来表示，是U 的极小值，()∑≠=ji ij x U 0021ϕ…………………………………………………………………… (3-1-5) 第二项是i j u 的线性项，它的系数为：()∑≠⎪⎪⎭⎫⎝⎛∂∂i j ij x 0ϕ，是所有其它原子作用在i 原子的合力的负值，当所有原子处在平衡位置上时，晶体中任一原子所受到的净作用力应为零，所以在式（3-1-4）中不存在位移的线性项。

位势的一维双原子链的晶格振动色散曲线

位势的一维双原子链的晶格振动色散曲线在固体物理学中，位势的一维双原子链的晶格振动是一个重要的问题，它的研究有助于我们理解和解释固体物理学中的一些关键现象。

晶格振动是晶体中的原子在平衡位置附近发生的小振动，它是晶体中热力学性质的基础。

在此基础上，我们可以研究晶体的声学性质、热学性质和磁性质等。

一维双原子链是由两种不同原子以交替排列形成的，其中每个原子的势能可以用简谐振子势能表示。

因此，这个系统的晶格振动可以通过一维简谐振子链模型来描述。

在这个模型中，每个原子都看做是一个简谐振子，相邻原子之间的作用力是势能函数的一阶导数，即表示为弹性常数k。

由于这个模型是一维的，因此在纵向方向和横向方向上的振动是独立的。

对于一维双原子链，晶格振动的频率可以用色散关系来描述。

色散关系是指在一个周向周期内波矢的变化引起的频率的变化。

在一维双原子链中，波矢k和频率ω之间的关系可以写成：ω^2(k) = (4k^2k^2 - k^2k^2)/(4m) +/- ((k^2k^2)^2 - (4k^2k^2 -k^2k^2)^2/16)^(1/2)/(4m)其中，m是原子的质量，+/-代表长波和短波模的解。

这个色散关系表明在一维双原子链中，存在两种不同类型的振动——声学振动和光学振动。

声学振动通常来源于原子的长程弹性相互作用，具有相同的相位和相同的振动方向。

这意味着在这种振动中，相邻原子之间的相对位移是相等的，它们沿着链的方向振动。

相反，光学振动通常源于原子之间的电磁相互作用，具有不同的相位和不同的振动方向。

这意味着，在这种振动中，相邻原子的相对位移是不相等的，它们在垂直于链的方向上振动。

对于一维双原子链的晶格振动，有两个特别有趣的点：无穷远波长和极短波长的情况。

在无穷远波长的情况下，声学振动和光学振动的频率都趋于零。

这意味着，在这种情况下，整个晶体的平移是可能的，并且这是一个有声波的晶体。

在另一方面，当波长很短时，声学振动的频率趋于一个有限值，而光学振动的频率则趋于无穷大。

3.2 一维双原子链


2β ω ≈ (aq) 2 m+M
2 −
或
2β ω− ≈ a q m+M
表明对于声学波频率正比于波数, 长声学波就是把 一维链看作连续介质时的弹性波, 这也就是为什么 称 ω－ 支为声学波的原因 对于长声学波, 当 q→0 时, ω－→0. 当 q 很小时, 因此
B →1 A −
−mω 2 A = β (e −iaq + eiaq ) B − 2β A 2 − iaq iaq −mω B = β (e + e ) A − 2β B
方程与 n 无关, 表明所有联立方程对 于格波形式的解都归结为同一对方程
可以看作是以 A、B 为未知数的线性齐次方程
( mω 2 − 2 β ) A + 2β cos aqB = 0 2β cos aqA + ( M ω 2 − 2β ) B = 0
β
iaq '
1 − ina ( q + q ') ) N ∑ e n
β
2m
Q(q ) (1 − eiaq ) Q(−q ) (1 − e − iaq ) ∑
q *
= ∑ Q(q)Q (q)
q
β
2m
( 2 − 2 cos aq )
1 1 2 2 * 2 = ∑ ωq Q(q )Q (q) = ∑ ωq Q(q) 2 q 2 q
势能
1 1 − inaq iaq − inaq ' iaq ' = β∑ (1 − e ) ∑ Q(q ')e (1 − e ) ∑ Q ( q )e 2 n Nm q q'
=
=
∑ Q(q) (1 − e ) Q(q ') (1 − e 2m

§3-2 一维双原子链的晶格振动解析


[mω2－（β1＋β2）]A1＋（β1e-iqa＋β2）eiqdA2＝0 （β1eiqa＋β2）e-iqdA1＋[mω2－（β1＋β2）]A2＝0
（3－22）
注意:该代数方程组与n无关。 A1、A2有非零 解的条件是其系数行列式为零：
mω2 －(β1＋β2) (β1e-iqa＋β2）eiqd ＝0 （β1eiqa＋β2）e-iqd mω2－(β1＋β2)

声学支格波仍描述原胞内原子的同相整体运动 光学支格波仍描述原胞内原子的反相运动。
三 、三维晶格振动
设实际三维晶体沿基矢 a1、a2、a3 方向的初基 原 胞 数 分 别 为 N1、N2、N3， 即 晶 体 由 N＝ N1·N2·N3初基原胞组成，每个初基原胞内含 s个原子。 1 .原子振动方向 一维情况下，波矢 q 和原子振动方向相同， 所以只有纵波。 三维情况下，有纵波也有横波。
当q→π/a时， 因 β2 >β1， 由式（3－23） ωO2 =（β1＋β2）/m+(β12＋β22＋2β1β2cosqa)1/2 /m 可得对于光学支格波
2 2 0＝ m
12
(3-32)
对于声学支格波,由(3-23)式 ωA2=（β1＋β2）/m (β12＋β22＋ 2β1β2cosqa)1/2 /m
2 / a N 2 / Na
注意:

这里的N为一维晶格的初基原胞数。每个q对 应两个频率（ωA和ω0），则共有2N组ω,q）， 所以一维双原子链有2N个格波，或说有2N个 简正模式。晶体中任何一原子的运动，为这 2N个格波所确定的谐振动的线性叠加。这时， 晶体的总自由度数也为2N，推广的结论：
允许的波矢数＝晶体的初基原胞数 格波总数＝晶体振动的总自由度数
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(3-42)
其中L1、L2、L3＝0，±1, ±2 · · · · · · ，b1、b2、b3是 倒格子基矢，N1，N2，N3是a1,a2,a3方向的初基原 胞数。
每一组整数（L1,L2,L3 ）对应一个波矢量q。将这 些波矢在倒空间逐点表示出来，它们仍是均匀分 布的。每个点所占的“体积”等于“边长”为(b1/N1)、 （b2/N2）、(b3/N3)的平行六面体的“体积”，它等 于：
V gi 3 2

dS q q
(3-47)
积分已变换到等频率面上了。
考虑到三维晶体中共有3S支格波，则格 波态密度函数为
V g ＝ g i ＝ 3 i 1 i 1 2
3s
3s
q
q i
dS
(3-48)
作业：1，2，3 思考题： 1.二维单原子阵列有几支声学支 格波？ 2. 声学格波是否就是声波？
1 2 A＝ 2 m 1 2
12
qa (3-28)
21 2 0＝ m
12
(3-29)
由此可知，在长波情况下，声学支格波具有声波的 线性色散关系：ωA＝υ0 q, 而且它的频率很低，可 以用超声波来激发，故得此名。光学支格波在q＝0 的附近ω0几乎与q无关，在q＝0处有极大值。

声学支格波仍描述原胞内原子的同相整体运动 光学支格波仍描述原胞内原子的反相运动。
三 、三维晶格振动
设实际三维晶体沿基矢 a1、a2、a3 方向的初基 原 胞 数 分 别 为 N1、N2、N3， 即 晶 体 由 N＝ N1· N2 · N3初基原胞组成，每个初基原胞内含s 个原子。 1 .原子振动方向 一维情况下，波矢 q 和原子振动方向相同， 所以只有纵波。 三维情况下，有纵波也有横波。
2 1 A＝ m
12
(3-33)
即在第一布里渊区边界上，存在格波频率“间隙” 在第一布里渊区边界上，由式（3－30）
A2 1e 2 iqd e iqa A 1e 2 1
iqa
可得 对光学支 A2＝－A1 e iqd 当d＜＜a , A2≈－A1 对声学支 A2＝A1 e iqd 当d＜＜a , A2≈A1 由于q→π/a，相邻原胞运动的相位差 qa→π。
设U1（na）表示平衡位置为na的A原子 的绝对位移，U2（na）表示平衡位置 为（na+d）的B原子的绝对位移。 仍采用简谐近似和近作用近似，则 运动方程为

1 na）＝－β2[U1(na)－U2(na)]－β1[U1(na)－U2（(n-1）a）] mU（

m U 2(na)＝－β2 [U2(na)－U1(na) ]－β1[U2(na)－U1((n+1)a)] (3-20)
2 / a N 2 / Na
注意:

这里的N为一维晶格的初基原胞数。每个q对 应两个频率（ωA和ω0），则共有2N组ω,q）， 所以一维双原子链有2N个格波，或说有2N个 简正模式。晶体中任何一原子的运动，为这 2N个格波所确定的谐振动的线性叠加。这时， 晶体的总自由度数也为2N，推广的结论：
3 .格波个数
三维晶格：3S支格波，一个q对应3S个ω值，即对应 3S个格波，允许的q取值数仍为初基原胞数N，则共 有3NS组（ωi,q）数组，晶体中有3NS个格波。
格波数＝晶格的总自由度数＝3NS
――――晶格振动理论中的普适结论。 晶体中任何一原子的实际运动是这 3NS 个格波所确 定的谐振动的线性叠加。
2 .格波支数
原则上讲，每支格波都描述了晶格中原子振 动的一类运动形式。初基原胞有多少个自由 度，晶格原子振动就有多少种可能的运动形 式，就需要多少支格波来描述。 一维单原子链：仅存在一支格波，且为声学 格波。 一维双原子链：存在两支格波―――声学波 和光学波。
定性地说，初基原胞质心的运动主要由 声学格波代表，初基原胞内两原子的 相对运动主要由光学格波代表 一维 S 原子链：存在 S 支格波―――其 中一支声学波，S－1支光学波。
允许的波矢数＝晶体的初基原胞数 格波总数＝晶体振动的总自由度数
以后可以看到，此结论对三维晶体也是适用的。
(二) .长波极限
当|q∣→0, λ→∞时, 相邻原胞间的振动相位差qa→0。 利用 cosqa ≈1 －（1/2）（qa）2 （1－x）1/2 ≈1－(x/2) （x为小量） 式（3－23）中 ωA2=（β1＋β2）/m- (β12＋β22＋2β1β2cosqa)1/2 /m 可简化为
三维晶体：原胞的总自由度数为3S,则 晶体中原子振动可能存在的运动形式 就有3S种，用3S支格波来描述。其中 在三维空间定性地描述原胞质心运动 的格波应有3支，也就是说应有3支声 学格波，其余3（S-1）支则为光学格 波。例如硅晶体属于金刚石结构，每 个初基原胞含两个原子，即S=2 , 它有 3支声学格波和3支光学格波。
b1 b2 b3 N N1 N N 3 2

（3－43）
式中Ω*是倒格子初基原胞的“体积”，也就是第一 布里渊区的“体积”，而Ω*＝（2π）3/ Ω ，所以 每个波矢q在倒空间所占的“体积”为：
2 2 ＝ ＝ N N V
* 3
(3-30)自推
正号对应声学支，负号对应光学支。当q→0时 A 2＝A 1 声学支 A2＝－A1 光学支 在长波极限情况下，

声学格波描写原胞内原子的同相运动， 光学格波描写原胞内原子的反相运动。
两支格波最重要的差别：
分别描述了原子不同的运动状态。
参见FD动画
45
（三）. q趋近第一布里渊区边界

该方程组有2N个方程，应有2N个解， 此时该晶体的总自由度数也为2N。

与一维单原子链比较，这里的近似条件相同，求解方 法类似，而前者有式（3－8）解的形式，它启发我们 作类似的试探解： U1(na)＝A1ei(qna－ωt)
U2(na)＝A2ei[q(na+d)－ωt] (3-21) 将其代入方程（3－20），并消去公因子ei(qna-ωt) 得到
[mω2－（β1＋β2）]A1＋（β1e-iqa＋β2）eiqdA2＝0 （β1eiqa＋β2）e-iqdA1＋[mω2－（β1＋β2）]A2＝0
（3－22）
注意:该代数方程组与n无关。 A1、A2有非零 解的条件是其系数行列式为零：
mω2 －(β1＋β2) (β1e-iqa＋β2）eiqd ＝0 （β1eiqa＋β2）e-iqd mω2－(β1＋β2)
V g i d＝ 3 2

d d
q
(3-46)
其中dq为倒空间体积元。
其中dSω是等频率面上的面元，dqn是dq 在等频率面法线方向上的分量。因此对于 一支格波
V g i d 3 2

ds
dS dqn
由梯度的意义，d可表示成 dω=∣▽qω(q)∣dqn
§3－2 一维双原子链的晶格振动
一、模型与色散关系
设一维晶体由N个初基原胞组成，每个初基 原胞有二个质量相等的原子，分别用A与B表 示，每个原子和它的左右近邻间距不等，弹 性系数也不等。晶格常数为a 。原子A与其右 侧B原子距离为d，弹性系数为β2 ，与其左侧 B原子的距离为（a-d）弹性系数为β1，为确定 起见，并设d<（a-d），β1<β2。
它具有q=0时，ωA ＝0的特征。 而光学支（Optical branch）格波 它具有q＝0, ω0≠0的特征。
ωO2 =（β1＋β2）/m +(β12＋β22＋2β1β2cosqa)1/2 /m
二、关于声学波和光学波的讨论
（一）格波数 与一维单原子链类似，可得： －π/a ＜q≤π/a (3-24) q＝2πm/Na m：整数 (3-25) 在第一布里渊区内，可取的q点数为
解得
ω2 = （β1＋β2）/m± (β12＋β22＋
2β1β2cosqa)1/2 /m （3－23）
即有两支ω～q 的色散关系。 当取“－”号时，ω记为ωA，称为声学支 取“＋”号时，ω记为ω0，称为光学支
声学支（Acousticbranch）
ωA2=（β1＋β2）/m -(β12＋β22＋2β1β2cosqa)1/2 /m
4．波矢取值
一维：－π/a ＜q≤π/a
在第一布里渊区内, q点的分布均匀, 每个q 点的“体
积”为2π／(Νa)＝b/N; 在第一布里渊区内q可取N个值；
三维：q仍在第一布里渊区内取值，共有N个值（初基原
胞数）
2 q m Na
m为整数
L3 L1 L2 q＝ b1 b2 b3 N1 N2 N3
3
(3-44)
其中V=NΩ为晶体体积。
在倒空间，波矢q的密度为
N N V ＝ ＝ 3 3 * 2 2
(3-45)
（四）格波的态密度函数
格波的态密度函数 g()，又称为模式密度，其 定义为 : 对给定体积的样品，在 附近
单位频率间隔内的格波总数。
对于第 i 支格波，在频率 到 ＋ d 之间的格 波数，就等于在q空间频率为到＋d这两个 等频率面之间所包含的q点数，即
入射红外光波与离子晶体中长光学波的共振 能够引起对入射波的强烈吸收，这是红外光 谱学中一个重要的效应。因为长光学波的这 种特点，所以称ω0 所对应的格波为光学波。 现在来考察一下两种原子的振幅比。把 式（3－23）代入（3－22）可得
A2 1e iqa 2 iqd e iqa A e 2 1 1
当q→π/a时， 因 β2 >β1， 由式（3－23） ωO2 =（β1＋β2）/m+(β12＋β22＋2β1β2cosqa)1/2 /m 可得对于光学支格波
2 2 0＝ m
12