材料力学讲稿:第13章 动荷载
- 格式:doc
- 大小:357.00 KB
- 文档页数:16

第十五章动荷载一、教学目标和教学内容1、教学目标通过本章学习,唤起学生对动荷载问题的注意。
让学生知道动荷载问题的两个方面,目前应当掌握在较简单的工程问题中,动荷载引起杆件的应力、应变和位移的计算。
对于材料在动荷载下的力学行为,以后根据工作的需要再进一步补充学习。
让学生掌握动荷载问题的基本知识,如杆件作等加速运动时的应力计算,作等速旋转圆盘的应力分析,简单的自由落体冲击和水平冲击,以及循环应力问题的有关概念。
能够深刻认识动荷系数概念,并能够熟练地进行杆件作等加速运动时的应力计算,作等速旋转圆盘的应力分析,完成简单的自由落体冲击和水平冲击的计算。
2、教学内容介绍杆件作等加速运动拉伸、压缩及弯曲时的应力计算。
介绍等角速度旋转的动荷应力计算。
讲解简单冲击时,能量守恒的基本方程,分别导出自由落体冲击和水平冲击时的动荷系数公式,及杆件经受冲击时的应力计算公式。
二、重点难点重点:建立三类动荷载概念。
掌握杆件作等加速运动时的应力计算。
作等速旋转圆盘的应力分析。
简单的自由落体冲击和水平冲击问题的计算难点:对动静法和动荷系数的理解。
对于动荷载问题与静荷载问题的联系与区别。
在简单冲击问题中,被冲击杆件冲击点的相应静荷位移的理解和计算,特别是水平冲击时的静荷位移的理解和计算。
三、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
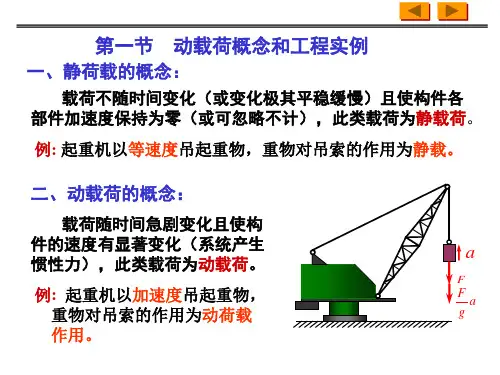
四、建议学时3学时五、实施学时六、讲课提纲(一)概念(动荷载的概念)1、静荷载:作用在构件上的荷载由零开始,逐渐(平缓、慢慢)地增长到最终值,以致在加载过程中,构件各点的加速度很小,可以不计;荷载加到最终值保持不变或变动的不显著的荷载,称之为静荷载。
2、动荷载:如果构件本身处于加速度运动状态(高层、超高层建筑施工时起吊重物;这些建筑物中运行的电梯—惯性力问题);或者静止的构件承受处于运动状态的物体作用(落锤打桩,锤头猛烈冲击砼桩顶—冲击问题);地震波引起建筑物晃动(构件在振动状态下工作—振动问题);机械零件在周期性变化的荷载下工作(交变应力疲劳问题),则构件受到荷载就是动荷载。









第十五章动荷载一、教学目标和教学内容1、教学目标通过本章学习,唤起学生对动荷载问题的注意。
让学生知道动荷载问题的两个方面,目前应当掌握在较简单的工程问题中,动荷载引起杆件的应力、应变和位移的计算。
对于材料在动荷载下的力学行为,以后根据工作的需要再进一步补充学习。
让学生掌握动荷载问题的基本知识,如杆件作等加速运动时的应力计算,作等速旋转圆盘的应力分析,简单的自由落体冲击和水平冲击,以及循环应力问题的有关概念。
能够深刻认识动荷系数概念,并能够熟练地进行杆件作等加速运动时的应力计算,作等速旋转圆盘的应力分析,完成简单的自由落体冲击和水平冲击的计算。
2、教学内容介绍杆件作等加速运动拉伸、压缩及弯曲时的应力计算。
介绍等角速度旋转的动荷应力计算。
讲解简单冲击时,能量守恒的基本方程,分别导出自由落体冲击和水平冲击时的动荷系数公式,及杆件经受冲击时的应力计算公式。
二、重点难点重点:建立三类动荷载概念。
掌握杆件作等加速运动时的应力计算。
作等速旋转圆盘的应力分析。
简单的自由落体冲击和水平冲击问题的计算难点:对动静法和动荷系数的理解。
对于动荷载问题与静荷载问题的联系与区别。
在简单冲击问题中,被冲击杆件冲击点的相应静荷位移的理解和计算,特别是水平冲击时的静荷位移的理解和计算。
三、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
四、建议学时3学时五、实施学时六、讲课提纲(一)概念(动荷载的概念)1、静荷载:作用在构件上的荷载由零开始,逐渐(平缓、慢慢)地增长到最终值,以致在加载过程中,构件各点的加速度很小,可以不计;荷载加到最终值保持不变或变动的不显著的荷载,称之为静荷载。
2、动荷载:如果构件本身处于加速度运动状态(高层、超高层建筑施工时起吊重物;这些建筑物中运行的电梯—惯性力问题);或者静止的构件承受处于运动状态的物体作用(落锤打桩,锤头猛烈冲击砼桩顶—冲击问题);地震波引起建筑物晃动(构件在振动状态下工作—振动问题);机械零件在周期性变化的荷载下工作(交变应力疲劳问题),则构件受到荷载就是动荷载。
3、动荷载与静荷载的区别静荷载:构件在静止状态下承受静荷载作用。
由零开始,逐渐缓慢加载,加到终值后变化不大、加速度很小,可以略去不计。
动荷载:在动荷载作用下,构件内部各质点均有速度改变,即发生了加速度,且这样的加速度不可忽略。
区别:加速度可忽略与不可忽略。
4、虎克定律的适用问题实验结果表明,只要应力不超过比例极限,虎克定律仍适用于动荷载的应力、应变的计算,弹性模量与静荷载的数值相同。
5、本章讨论的问题⑴惯性力问题:构件在加速度运动时的应力计算;构件在匀速转动时应力计算(构件上各点有向心加速度)。
⑵冲击问题:垂直冲击;水平冲击。
(二)惯性力问题1、惯性力的大小与方向对于加速度为a的质点,惯性力等于质点的质量m与其加速度a的乘积,即惯性力大小。
a m F I ⨯= ─────────────(a)若构件的重量为G,重力加速度为g ,则质点的质量gGm =─────────────(b) 则质点的惯性力a gGF I ⨯=─────────────(c) 惯性力的方向与加速度a 的方向相反。
2、动静法——达朗贝尔原理。
达朗贝尔原理指出,对作加速度的质点系,若假想地在每一质点上加上惯性力,则质点系上的原力系与惯性力系组成平衡力系。
这样,就可把动力学问题在形式上作为静力学问题来处理。
这就是动静法。
3、构件在加速度直线运动时的应力和变形计算。
⑴动荷载系数K d例如有一绳索提升重量为G 的重物(如下图)。
图13-1则∑=0y F0=⨯--a g G G F Nd )1(ga G a g G G F Nd +=⨯+= 所以,绳索中出现的动应力为)1()1(gag a A G A F st Nd d +=+==σσ ────────────⑴ 式中的AGst =σ是静力平衡时绳索中的静应力。
若令⑴式括号内ga +1为d K , 那么⑴式即为st d d k σσ⨯=────────────────────⑵式中的d k 称为动荷系数⑵式表明:绳索中的动应力d σ=静应力st σ乘以动荷载系数d k 。
同理:绳索中的静伸长st l ∆乘以动荷载系数d k =绳索的动伸长d l ∆,即st d d l K l ∆⋅=∆────────────────────⑶同理:st d d K εε⋅=─────────────────────⑷⑵匀加速直线运动构件的应力计算一直杆AB 以匀加速a 向上提升(见下图);设杆长为l ,横截面积为A ,材料的容重为r ,求杆内的动应力?=d σ图13-2解:①用截面法截出杆的下段 ②设截面上的轴向力为Nd F③该段在Nd F 、自重rAx 和惯性力a grAx⋅作用下形成平衡力系(图b ) 由静力平衡条件得:+=rAx F Nd =⋅a grAx )1(g arAx +若用AF Ndd =σ代表横截面上的正应力,则 )1(ga rx d +=σ ──────────────────(A)∵静应力rx A rAx st ==/σ ∴st d st d K ga σσσ=+=)1(由(A)式可知,杆内的正应力沿杆长按直线规律变化,见图c 4、构件在匀速转动时的应力计算当构件作定点匀速转动时,构件上各点有向心加速度2ωR a n =式中的R 为质点到转轴的距离(圆环的平均半径)图13-3离心惯性力沿圆环中心线均匀分布,其集度为222ωωD g Ar R g Ar a g Ar q n d ⨯=⨯=⨯=则环向应力2224222ωωσθ⨯=⋅⋅⋅==grD A DD g Ar A D q o ─────────────⑴∵线速度ω2DV =∴环向应力计算式也可写成: 2υσθ⨯=gr───────────⑵ 其强度条件:][422σωσθ≤⋅=grD ────────────────⑶ ][2συσθ≤⋅=gr ─────────────────⑷由⑶式可求转速,∵n πω2=,则⑶式可写成rg D n ⨯==][12σππω───────────────⑸ 由⑷式可求容许线速度rg⨯=][][συ──────────────────⑹例题13-1 在AB 轴的B 端有一个质量很大的飞轮(如下图)。
与飞轮相比,轴的质量可忽略不计。
轴的另一端A 装有刹车离合器。
飞轮的转速为min /100r n =,转动惯量为2S M KN ⋅⋅=5.0x I 。
轴的直径mm d 100=,刹车时使轴在10秒内均匀减速停止。
求轴内最大动应力。
图13-4解:⑴飞轮与轴的转动角速度为s rad n o /31030100602πππω=⨯==⑵当飞轮与轴同时做均匀减速转动时,其角加速度为21/3103100s rad toππωωε-=-=-=(其中负号表示ε与oω的方向相反,如上图)⑶按动静法,在飞机上加上方向与ε相反的惯性力偶矩d M ,且m KN ⋅=--=-=35.0)3(5.0ππεx d I M⑷设作用于轴上的摩擦力矩为t M ,由平衡方程∑=0x M ,设:m KN ⋅==35.0πd t M M ⑸AB 轴由于摩擦力矩t M 和惯性力偶矩d M 引起扭转变形,横截面上的扭矩为T M ,则m KM ⋅==35.0πd T M M ⑹横截面上的最大扭转剪应力为2.67MPa Pa 103=⨯=⨯⨯==-623max 1067.2)10100(1635.0ππτp rW M例题13-2 图示结构中的轴AB 及杆CD ,其直径均为d=80mm ,s /40=ω,材料的MPa 70][=σ,钢的容重3KN/m 4.76=γ,试校核AB 、CD 轴的强度。
解法之一:解:1、校核AB 轴的强度(AB 轴的弯曲是由于CD 杆惯性力引起的,因为CD 杆的向心加速度引起了惯性力)图13-5⑴CD 杆的质量:gl r A gG m CD⋅⋅==⑵CD 杆的加速度:CD R a ⋅=2ω ⑶CD 杆引起的惯性力I F ;KN 28.1126.0408.96.0104.76408.0232=⨯⨯⨯⨯⨯⨯=⋅=πa m F I ⑷AB 轴的M kN ⋅=⨯⨯==38.342.11028.1143max l F M I d ⑸AB 轴的][MPa σπσ 3.6708.0321038.333max =⨯⨯==W M d d 2、校核CD 杆的强度(I Nd F F =受拉,危险截面在C )][25.2408.01028.1133σπσ MPa =⨯⨯===AF A F I Nd d解法之二:图13-6解:沿CD 杆轴线单位长度上的惯性力(如图b所示)为N/m x x l l x q CDCDd 32321061440)104.7608.04()(⨯=⨯⨯⨯⨯⨯=π当0=x 时,0=d q当m x 04.0=时(c 截面处),N/m 3106.24⨯=d q 当m x 6.0=时,N/m 3105.368⨯=d q CD 杆危险面C 上轴力和正应力分别为KN3.1102.01.110]104.76)04.06.0(08.04[)]04.06.0()105.368106.24[(213233max =+=⨯⨯-⨯⨯+-⨯⨯+⨯=πNd F MPa 9.2108.04103.11023max max =⨯⨯==πσA F N d(三)冲击荷载落锤打桩、汽锤锻打钢坯、冲床冲压零件,转动的飞轮突然制动、车辆紧急刹车都属于冲击荷载问题。
1、垂直冲击(冲击物为自由落体)图13-6设有一重物Q 从高处为H 处自由落下(如图),冲击到被冲击物体的顶面上,则其动荷载系数std HK δ211++=式中的EAQlEA l F l N st ==∆=δ ─────构件在静荷载作用时的静位移。
⑴若H=0时(即突加荷载——荷载由零突然加到Q 值), 则2=d K st st d d K δσσ2== st st d d K δδδ2==即突加荷载作用下,构件的应力与变形比静荷载(由值逐渐Q −−→−0)时要大一倍。
⑵若102 stHδ时,则std HK δ21+≈⑶若1002 stHδ时std HK δ2≈⑷若已知在冲击开始时冲击物自己落体的速度V ,则std HK δ21+=中的高度H 可用g V 22来代替,即std g V K δ211++=2、水平冲击水平冲击时(图a 、b 所示)的动荷系数std g VK δ=─────────────────⑺图13-73、冲击荷载作用下的动位移、动应变、动应力st d d K δδ= st d d K εε= st d d K σσ=4、受冲击时构件的强度条件:][σσσ≤=st d d K例题13-3 试校核图示梁在承受水平冲击荷载作用时的强度。