2010年福建省厦门中考数学试卷(word版含答案)

秘密★启用前2010年南平市初中毕业生综合测试数学本试卷共三大题25小题，共4页，満分150分.考试时间120分钟.1. 答卷前，考生务必在答题卡第1面.第3面、第5面上用黒色字迹的钢笔或签字笔填写自己的考 生号、姓名；填写考场试室号.座位号,再用2B 铅笔砂寸应这两个号码的标号涂黑2. 选择题每小题选岀答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黒；如需改动，用橡皮擦 干净后，再选涂其他答案标号；不自结在试卷上.3. 非选择题必须用黒色宇迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图.答案必须写在 答题卡各题目指定区域內的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；改动的答 案也不§礎岀指定的区域.不准使用铅笔、圆珠笔和涂改液.不按以上要求作答的答案无效.4. 考生龙须保持答题卡的整洁，考试结束后，将本试卷和答题L 并交回.一. 磐题（本大题共1CP 隠，每小题3分，共30分.在每小题给岀的四个选项中，只有一项是符合 题目要求的）1、a 是3的倒数，那么a 的值等干（* ）B. -3C. 3D. 13 既是翔寸称图形又是中心对称图形的是（*）3s 下列运算正确的是（* ）7、如果两圆半径分别为3和4,圆心距为6,那么这两圆的位置关系是 （* ）A 、相交内切Cs 外离D>外切c ■32、下列图形中, A. (J2+1)^/2 ・1)=1 Bs (33)2 = 35D>x 8 x 4= x 2 1A. y=-B X-1 C2、y =—C 、y =—X XD 、严*X5.下列一元二次方程中， 有两个不相等的实数根的是（*）A. x 2 + 2x+1 = 0Bs x 2 + 2 = 0C 、x 2 — 3 = 0Ds x 2 + 2x + 3 = 0B.C ・ D.4、下列函数中，图彖经过点（-1, 2）的反比例函数解析式是（* ）6、如图1,己知？屈C 为直角三角形，? 090。

2010年福建省泉州市初中毕业、升学考试数 学 试 题（满分：150分；考试时间：120分钟）友情提示：所有答案必须填写到答题卡相应的位置上.毕业学校 姓名 考生号 一、选择题（每小题3分，共21分） 每小题有四个答案，其中有且只有一个答案是正确的．请在答题卡上相应题目的答题区域内作答，答对的得4分，答错、不答或答案超过一个的一律得0分． 1．10的相反数是 ( ). A.110B. 110-C. 10- (D) 102. 下列各式，正确的是（ ）A.12≥-B. 23-≥-C. 23≥D.23≥3．9的平方根是（ ）.A. ±B.C. ±3D. 34．把不等式1x ≥-的解集在数轴上表示出来，则正确的是().5．下面左图是由六个相同正方体堆成的物体的图形，则这一物体的正视图是（ ）.6．新学年到了，爷爷带小红到商店买文具.从家中走了20分钟到一个离家900米的商店，在店里花了10分钟买文具后，用了15分钟回到家里.下面图形中表示爷爷和小红离家的距离y （米）与时间x （分）之间函数关系的是（ ）.7．如图所示，在折纸活动中，小明制作了一张A B C △纸片，点D E 、分别是边AB 、AC 上，将A B C △沿着D E 折叠压平，A 与'A 重合，若=70A ︒∠，则1+2∠∠=（ ）A. 140︒B. 130︒C. 110︒D. 70︒二、填空题（每小题4分，共40分）在答题卡上相应题目的答题区域内作答． 8．方程280x +=的解是 .9．据了解，今年泉州市中考考生大约101000人，将101000用科学记数法表示为 .10. 四边形的外角和等于 度.11. 某小组5名同学的体重分别是（单位：千克）：46,46,45,40,43，则这组数据的中位数为千克.12. 如图，已知：直线AB ∥CD ，︒=∠651，则=∠2.13. 如图，点A 、B 、C 在⊙O 上，︒=∠45A ，则=∠BOC .14. 计算：111a a a +++= .15. 在一次函数32+=x y 中，y 随x 的增大而（填“增大”或“减小”），当50≤≤x 时，y 的最小值为.16. 现有四条钢线，长度分别为（单位：cm ）7、6、3、2，从中取出三根连成一个三角形，这三根的长度可以为.（写出一种即可）17. 如图，两同心圆的圆心为O ，大圆的弦AB 切小圆于P ，两圆的半径分别为2 和1，则弦长AB =；若用阴影部分围成一个圆锥，则该圆锥的底面半径为.(结果保留根号)三、解答题（共89分）在答题卡上相应题目的答题区域内作答．18.（9分）计算：01|3|(3)42π--+--⨯.19.（9分）先化简，再求值:2(1)(1)(1)x x x x +-+-，其中2x =-.20.（9分）吴老师为了解本班学生的数学学习情况，对某次数学考试成绩(成绩取整数，满分为100分)作了统计，绘制成如下频数分布表和频数分布直方图．请你根据图表提供的信息，解答下列问题：（1）求频率分布表中a、b、c的值；并补全频数分布直方图；（2）如果用扇形统计图表示这次数学考试成绩时，那么成绩在69.5～79.5范围内的扇形圆心角的度数为多少度？21.（9分）如图, 正方形ABCD中, E是CD上一点, F在CB的延长线上,且BFDE=。

厦门市思明区初中毕业班质量检查数学试题（满分： 150分；考试时间：120分钟）考生注意：本学科考试全部答案要求填在答题卡的相应答题栏内，否则不能得分.一、选择题（本大题有7小题，每小题3分，共21分.每小题都有四个选项，其中有且只有一个选项是正确的） 1. +4的相反数是（ ）A. -4B. +4C. ±4D. 2 2. 要使分式2xx +有意义，则x 的取值范围是（ ） A ．2x ≠ B ．2x ≠- C ．2x >- D ．2x <-3.下列长度的三条线段能组成三角形的是（ ）A. 3,4,8B. 5,6,11C. 2,2,6D. 5,6,94.若两圆的半径分别为5cm 和3cm ，且它们的圆心距为2cm ，则这两圆的位置关系是（ ） A.外切 B.相交 C.内切 D.内含5. 下列说法正确的是（ ）A.为了了解我市今夏冰淇淋的质量，应采用普查的调查方式B.想了解一个同学5次考试成绩的稳定程度，只需关注该生这5次考试成绩的中位数C.随意翻到一本书的某页，这页的页码是偶数，这一事件是随机事件D.某种彩票中奖的概率是1%，买100张该种彩票一定会中奖 6. 下列语句中一定正确的是（ ） A.相等的角是对顶角B.过直线MN 外的一点P 分别作PA MN ⊥，PB MN ⊥,垂足分别为A 、BC.两条直线被第三条直线所截，内错角相等D.锐角的补角一定是钝角7. 已知ABC ∆，D 是边AB 上的一点，DE BC ∥交AC 于点E ，DF AC ∥交BC 于点F ，若ADE ∆、DBF ∆的面积分别为1和2，则四边形DECF 的面积为( )A.3B.2C.D.二、填空题（本大题有10小题，每题4分，共40分） 8. 2-= .9. 计算：18= .(第7题)10. 分解因式：22x x -= .11.如图，在ABC ∆中，AD 平分BAC ∠且交BC 点D ，B ∠= 40°，CAD ∠= 30°，则ADC ∠的度数是 .12.在厦门园博苑草莓采摘园，五位游客每人各采摘了一箱草莓，草莓质量分别为（单位：千克）： 5， 2， 3， 5， 5，则这组数据的平均数和中位数分别为 .13. 2010年5月1日至10月31日期间，第41届世界博览会在上海市举行.中国馆由国家馆、地区馆和港澳台馆三个部分组成，三个场馆的建筑面积如表格所示，则中国馆的总建筑面积用科学记数法表示为 平方米.14. 75°的圆心角所对的弧长是25π，则此弧所在圆的半径为 ．15.写出一个被开方数中含有字母x 的二次根式（要求：不论x 取任何实数，该二次根式都有意义） ．16.已知等腰梯形ABCD ，AD BC ∥，4AD =，60B ∠=︒，AC 为DCB ∠的平分线， E 是AB 中点，DF 是梯形的高，ABCD S = ；若在直线AC 上找一点M ，使EM FM +的三、解答题（本大题有9小题，共89分） 18.(本题满分18分) （1）计算：()21252sin 305--⨯+︒. （2）计算：221111a a a a a a -÷----．(第11题)(第13题) (第16题)（3）解方程组123x y x y +=⎧⎨+=⎩ .19.( 本题满分8分) 不透明的布袋中有2个红球，3个绿球，4个白球，它们只有颜色上的区别.闭着眼睛从袋子中随机取出一个球. （1）求取出绿球的概率；（2）怎样通过改变各色球的数目，使取出每种颜色的球的概率都相等，请写出一个方案. 20．(本题满分8分)如图，四边形ABCD 的对角线AC 与BD 相交于点O ，12∠=∠，34∠=∠．（1）求证：ABC ADC △≌△；（2）若14∠=∠，6AC BD ==，求四边形ABCD 的周长．21. (本题满分8分)已知反比例函数的图象过点()1,2A -. （1）求这个反比例函数的关系式；（2）如果直线()20y ax a =+≠与该双曲线没有交点，求a 的取值范围. 22. （本题满分8分）如图，AB 为O 的弦，C 为劣弧AB 的中点， （1）若O 的半径为5，8AB =，求tan BAC ∠；（2）若DAC BAC ∠=∠，且点D 在O 的外部，判断AD 与O 的位置关系，并说明理由.23. （本题满分9分） 某市拟将一长100米，宽80米的矩形空地建成活动广场，出于绿化和安全的考虑，要求出入口宽度既不小于40米，也不大于70米.王工程师的设计方案如图所示：整个图形既是轴对称图形又是中心对称图形，其中阴影部分为矩形绿化区，空白部分为活动区，且活动区四周的出入口一样宽.（1）若四个绿化区的总面积．．．为800平方米，求出入口宽度； （2）预计活动区每平方米造价60元，绿化区每平方米造价50元．如果市政府提供45万元建设经费，按照王工程师的设计方案，是否还需另行筹措经费？D C BA O 12 3 4 (第20题)(第22题)(第23题)24.（本题满分9分）如图，ABC ∆中，AB AC =,AD 、AE 分别是BAC ∠及其外角CAF ∠的平分线，CE AE ⊥. （1）求证：AB DE =；（2）若48ABC S ∆=,8AD =,P 为线段CE 上的动点，设x 为点P 到直线AC 的距离，y 为点P 到直线AB 的距离，求y 关于x 的函数关系式，并写出自变量x 的取值范围.25.（本题满分10分）已知正方形ABCD 的边长为2，点E 、F 均在直线BD 上，且135EAF ∠=︒，:1:2EB DF =.（1） 求CF ；（2） 在直线BD 上是否存在点P ，使A 、E 、P 三点围成的三角形是直角三角形？若存在求出EP 的长，不存在请说明理由.26．（本题满分11分）已知，平面直角坐标系上有(,0)(0,)(,0)A a B b C b -、、三点，且0a b ≥＞， 抛物线()()()()22y x x m n n m =----- （m 、n 为常数，且220m n +≥＞）经过点A 和点C ，顶点为P .（1）当m 、n 满足什么关系时，AOB S ∆最大； （2）如图，当ACP ∆为直角三角形时，判断以下命题是否正确：“直角三角形DEF 的三个顶点都在这条抛物线上，且DE x ∥轴，那么ACP ∆与DEF ∆斜边上的高相等”，如果正确请予以证明，不正确请出举反例.(第25题)(第26题)(第24题)厦门市思明区2010届初中毕业班质量检查数学参考答案及评分标准说明：1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分；2．评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅．如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定后继部分的给分，但原则上不超过后继部分应得分数的一半； 3．解答题评分时，给分或扣分均以1分为基本单位．8. 2. 9. 10. )12(-x x . 11.70°. 12. 4千克，5千克. 13.410.57⨯ 14. 60. 15. 如2x ，12+x 等. 16. 312；6 . 17. (-2，-2)、(-1，-3)、(0，-2)、(1，1).（第12题没单位只扣1分，第17题写对一个给一分，若写错一个整题不给分） 三、解答题(本大题有9小题，共89分) 18. (本题满分18分) (1)解：()21252sin 305--⨯+︒ ＝4－1 +2 ×12 ……3分＝4－1＋1 ……4分 ＝4 ……6分(2)解：221111a a a a a a -÷---- ＝(1)11(1)(1)1a a a a a a a -÷--+-- ……8分 ＝(1)(1)11(1)1a a a a a a a +----- ……9分＝1111a a a +--- ……11分 =1-a a……12分(3) 解方程组123x y x y +=⎧⎨+=⎩①②解法1：由①得y x -=1 ③ ……13分 把③代入②得3)12=+-y y （ ……14分 ∴ 1-=y ……16分 把 1-=y 代入③得2=x ……17分∴ ⎩⎨⎧-==12y x ……18分解法2：由②-①得2=x ……14分 把 2=x 代入①得1-=y ……16分∴ ⎩⎨⎧-==12y x ……18分19．(本题满分8分) (1)解：P (取出绿球)＝3193= . ……4分 (2)解：如在不透明的布袋中，放入一个红球，取出一个白球. ……8分 或：在不透明的布袋中，取出一个绿球和二个白球. ……8分20．(本题满分8分) (1)证明：∵∠1＝∠2， ∠3＝∠4 ……1分 又∵AC ＝AC ， ……2分 ∴ABC ADC △≌△. ……3分 (2)证明：∵∠1＝∠4又∵∠1＝∠2∴ ∠2＝∠4.∴AD ＝DC . ……5分D CB A O 12 3 4 (第20题)同理AB ＝B C由（1）知ABC ADC △≌△ ∴BC ＝CD∴AB =AD ＝BC ＝CD .∴四边形ABCD 是菱形 ……6分 ∴ AC BD ⊥ ,∵6AC BD ==∴12AO AC ==132BO BD ==∴6AB == ……7分∴四边形ABCD 的周长=4 AB =24 ……8分21．(本题满分8分)(1) 解：设反比例函数的关系式是xky =……1分 ∵反比例函数的图象过点()1,2A -∴2-=k ……2分 ∴xy 2-= ……3分 (2) 由题意得22y ax y x =+⎧⎪⎨=-⎪⎩……4分∴22ax x+=-整理得2220ax x ++= ……6分∵直线2y ax =+与该双曲线没有交点，且0a ≠∴480a ∆=-＜ ……7分 ∴12a ＞即a 的取值范围为12a ＞. ……8分22．(本题满分8分)(1)解： ∵AB 为⊙O 的弦，C 为劣弧AB 的中点,8AB = ∴OC AB ⊥于E ∴ 142AE AB == ……1分 又 ∵5AO = ∴3OE = ……2分 ∴ 2CE OC OE =-= ……3分 在Rt △AEC 中,21tan 42EC BAC AE ∠=== ……4分 (2)AD 与⊙O 相切. ……5分 理由如下： ∵OA OC = ∴C OAC ∠=∠∵由（1）知OC AB ⊥∴ ∠C+∠BAC ＝90°. ……6分又∵BAC DAC ∠=∠∴90OAC DAC ∠+∠=︒ ……7分 ∴AD 与⊙O 相切. ……8分 23.(本题满分9分)（1）解：∵整个图形为既是轴对称图形又是中心对称图形∴四个矩形绿化区全等 ……1分 设活动广场的出入口的宽度为x 米，依题意，得80028021004=-⨯-⨯xx ……3分 解得舍去）(120,6021==x x 答：活动广场的出入口的宽度为60米. ……4分 （2）解：设总造价为元y ，依题意，得)2802100480100(602802100450xx x x y -⨯-⨯-⨯⨯+-⨯-⨯⨯= ……5分 =480000)80)(100(10+---x x=48100090102+--）（x ……6分 ∵100,-＜开口向下(第22题)E∴当90x ＜时，的增大而增大随x y ……7分 又∵出入口宽度不小于40米，也不大于70米∴4070x ≤≤ ∴当米时40=x ，所需造价最少，=y 456000元 ……8分 ∵450000456000＞∴按照王工程师的设计方案，还需另行筹措经费. ……9分∴四边形AECD 是矩形∴ AC = DE ……3分∴AB =DE ……4分 (2)解法1： ∵△ABC 中，AB=AC ，AD 平分∠BAC ∴AD ⊥BC ,12DC BC =又∵48ABC S ∆=,8AD =∴BC ＝12. ∴DC ＝BD =6 ∴AB =10过点P 分别作PG DE PH AC ⊥⊥，,分别交DE 、AC 于点G 、H .延长PG 交AB 于M . 过点D 作DN ⊥AB 于点N . ∵AD ⊥BC∴1122ABD S AB DN BD AD ∆== ∴245DN =. ……5分∵ 由（1）知四边形ADCE 是矩形,设AC 与DE 相交于O ∴5OE OC ==∴AE =DC 又∵DC ＝BD∴AE =BD又∵由（1）知AB =DE∴四边形ABDE 是平行四边形 ∴AB ∥DE又∵,DN AB GM AB ⊥⊥∴DN GM ==245……6分 连结PO ，则ADCE 14POE POC S S S += 矩形∴1116812224OE PG OC PH +=⨯⨯= ∴11245+5()12225x y ⨯⨯-= ……7分 整理得485y x =-+（2405x ≤≤） ……9分解法2：过点P 分别作PM AB PH AC ⊥⊥，,分别交AB 、AC 于点M 、H .ABP CBP AEP ABCE S S S S ∆∆∆=++梯形 ……5分同解法1，得72ABCE S =梯形1102ABP S y ∆=⨯⨯ ……6分 易证AEC PHC △∽△ ∴610PH PC = ∴53PC x =，583PE x =- ……7分∴10CBP S x ∆=，245AEP S x ∆=- ……8分 ∴5y +10x +(245)x -=72 ∴485y x =-+（2405x ≤≤） ……9分25．(本题满分10分)(1)解： ∵四边形ABCD 是正方形 ∴ 90BAD ∠=︒, 45ABD ADB ∠=∠=︒∴45EAB BEA ∠+∠=︒∵135EAF ∠=︒∴45EAB DAF ∠+∠=︒∴AEB FAD ∠=∠ ……1分又∵135ABE FDA ∠=∠=︒，∴AEB FAD △∽△ ……2分 ∴EB AB AD DF= 又∵:1:2EB DF =，2AB AD ==∴EB DF =……3分连结AC 交EF 于O ,则在正方形ABCD 中，AC BD ⊥,CO DO ==∴OF =∴在Rt COF 中，CF =……4分(2)解：在直线BD 上存在点P ，使A 、E 、P 三点围成的三角形是直角三角形 ①若90APE ∠=︒,则P O 点与点重合∵在正方形ABCD 中，AC BD ⊥，交BD 于O ,∴90AOE ∠=︒.∴P O 点与点重合 ……5分在Rt △AOE 中,由（1）知EB BO ==∴EP =……6分②若90PAE ∠=︒，则过 A AP AE BD P ⊥作，交直线于……7分∵AO BD ⊥∴Rt Rt AOE POA △∽△……8分∴ AO PO EO AO=∴OP =∴2EP =……9分 ③135EAF AEP ∠=︒∠ ，∴ 必小于45°，此时在直线BD 上不存在点P ，使A 、E 、P 三点围成的三角形是直角三角形∴EP =2EP =……10分 26．(本题满分11分)(1)解：∵()()()()22y x x m n n m =----- ∴ 整理得22(2)(2)y x m x n nm n =-+--- ……1分 ∵ 抛物线经过(,0)(,0)A a C b 、∴当0y =时，a b 、满足方程22(2)(2)0x m x n nm n -+---=，且12AOB S ab = ∴2(2)ab n m n =-++= 2222)(24m m n ++--+（） ……3 分 ∵-1＜0，m 、n 为常数，且220m n +≥＞∴当 n ＝22m +时， ab 的值最大，即AOB S ∆最大 ……4 分 ∴ 22m n +=时， AOB S ∆最大 ……5分(2)解：命题是正确的.∵由(1)知a b 、满足方程22(2)(2)0x m x n nm n -+---=∵220m n +≥＞，0a b ≥＞∴2,a m n b n =+-= ……6分∴22AC m n =+-∵抛物线22(2)(2)y x m x n nm n =-+--- ∴顶点()224(2)22(,)24n mn n m m P -++-++ ∵ 点P 是抛物线顶点，且点A 与点C 是对称点.又∵ACP ∆为直角三角形∴ACP ∆为等腰直角三角形∴ACP ∆斜边上的高=12AC ∴()224(2)22242n mn n m m n -++-++--= ∴122,22m n m n ==-. ……7分∵若22m n =-，则,a n b n ==.∴点A 与点C 重合，不合题意舍去.∴2m n = ……8分∴ACP ∆斜边上的高=12222m n AC +-=1= ……9分 ∵DEF ∆为直角三角形，且DE x ∥轴，过F 作FG DE ⊥于G设抛物线22(22)(2)y x n x n n =-+++上的点112133(,),(,),(,)D x y E x y F x y 且12x x ＜∴1222x x n +=+∴31(,)G x y∴3123,,DG x x EG x x =-=-∴13FG y y =-=1313()(22)x x x x n -+--1332()()x x x x =--又 ∵Rt DGF Rt FGE ∽∴ GF GE DG GF= 2GF DG GE = ∴∴2231321332()()()()x x x x x x x x --=-- ……10分∵3132()()0x x x x --≠∴3132()()1x x x x --= ∴1FG =∴DEF △斜边上的高=ACP ∆斜边上的高=1 ……11分∴直角三角形DEF 的三个顶点都在这条抛物线上，且DE x ∥轴，那么ACP ∆与DEF ∆斜边上的高相等.。

2010年福建省泉州市初中毕业、升学考试数 学 试 题（满分150分；考试时间：120分钟）友情提示：所有答案必须填写到答题卡相应的位置上.毕业学校_____________姓名_______________考生号_____________一、选择题（每小题3分，共21分）：每小题有四个答案，其中有且只有一个答案是正确的. 请在答题卡上相应题目的答题区域内作答，答对的得3分，答错、不答或答案超过一个 的一律得0分.1. 10的相反数是（ ）. A.110 B.110- C.10- D.10 2.下列各式，正确的是（ ）.A.21->B.32->->2>3. 9的平方根是（ ）.A.3±B.3C.4.把不等式1x -≥的解集在数轴上表示出来，则正确的是（ ）.5.下面左图是由六个相同正方体堆成的物体的图形，则这一物体的正视图是（ ）.6. 新学年到了，爷爷带小红到商店买文具，从家中走了20分钟到一个离家900米的商店，在店里花了10分钟买文具后，用了15分钟回到家里.下面图形中表示小红和爷爷离家的距离y （米）与时间x （分）之间函数关系的是（ ）.A. C.D. B. A. B. D. C. B. C. D.A. y （米）y （米）y （米）y （米）x （分） x （分） x （分） x （分）7.如图所示，在折纸活动中，小明制作了一张ABC △纸片，点D E 、分别在AB AC 、上，将ABC △沿着DE 折叠压平，A 与A '重合，若70A ∠=°，则12∠+∠=（ ）. A.70° B.110° C.130° D.140°二、填空题（每小题4分，共40分）：在答题卡上相应题目的答题区域内作答. 8.方程280x +=的解是____________. 9.据了解，今年泉州市中考考生大约101 000人，将101 000用科学记数法表示为_________. 10.四边形的外角和等于___________度.11.某小组5名同学的体重分别是（单位：千克）：40，43，45，46，46，则这组数据的中位 数为___________千克.12.如图，直线AB CD ∥，65∠=°，则2∠=__________.13.如图，点A B C 、、在O ⊙上，45A ∠=°，则BOC ∠=___________.14.计算：111aa a +++=___________. 15.在一次函数23y x =+中，y 随x 的增大而__________（填“增大”或“减小”）；当05x ≤≤时，y 的最小值为___________.16.现有四根钢线，长度分别为（单位：cm ）：7、6、3、2，从中 取出三根连接成一个三角形，这三根的长度可以为__________ cm.（写出一种即可）17.如图，两个同心圆的圆心为O ，大圆的弦AB 切小圆于P ， 两圆的半径分别为2和1，则弦AB 的长为________；若用阴影部分围成一个圆锥，则该圆锥的底面半径为_______. 三、解答题（共89分）：在答题卡上相应题目的答题区域内作答. 18.（9分）计算：013(π3)42.--+-⨯19.（9分）先化简，再求值：2(1)(1)(1)x x x x +-+-，其中 2.x =-C BD B AB B2 1 （第12题图） AB BC B O B （第13题图）OA BB P B（第17题图） （第7题图） A B B C B E BD 12 A '20.（9分）吴老师为了解本班学生的数学学习情况，对某次数学考试成绩（成绩取整数，满 分为100分）作了统计，绘制成如下频率分布表和频数分布直方图. 请你根据图表提供的信息，解答下列问题：（1）求频率分布表中a b c 、、的值，并补全频数分布直方图；（2）如果用扇形统计图表示这次数学考试成绩时，那么成绩在69.5~79.5范围内的扇形21.（9分）如图，在正方形ABCD 中，E 是CD 上一点，点F 在CB 的延长线上，且.DE BF（1）求证：ADE ABF △≌△；（2）问：将ADE △顺时针旋转多少度后与ABF △重合，旋转中心是什么？22.（9分）在一个黑色的布口袋里装有白、红、黑三种颜色的小球，它们除了颜色之外没有 其它区别，其中白球2只、红球1只、黑球1只.袋中的球已经搅匀. （1）随机地从袋中摸出1只球，则摸出白球的概率是多少？ （2）随机地从袋中摸出1只球，放回．．搅匀再摸出第二只球，请你用画树状图或列表的方 法表示所有等可能的结果，并求两次．．都摸出白球．．的概率.A DB （第21题图）C B EB BB FB23.（9分）如图，在梯形ABCD中，90A B AB ∠=∠==°，点E 在AB 上， 4567.AED DE CE ∠===°，， 求：AE 的长和sin BCE ∠的值.24.（9分）某蔬菜公司收购一批蔬菜，计划用15天加工后上市销售.该公司的加工能力是： 每天可以精加工3吨或者粗加工8吨，且每吨蔬菜精加工后的利润为2 000元，粗加工后 的利润为1 000元.已知该公司售完这批加工后的蔬菜，共．获得利润100 000元. 请你根据以上信息，解答下列问题：（1）如果精加工x 天，粗加工y 天，依题意填写下列表格：（2）求这批蔬菜共．多少吨.25.（12分）我们容易发现：反比例函数的图象是一个中心对称图形.你可以利用这一结论解 决问题.如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x 轴所在的直线绕着原点O 逆时针旋转α度角后的图形.若它与反比例函数y =的图象分别交于第一、三象限 的点B D 、，已知点(0)(A m C m -，、,0)（m 是常数，且0m >）.（1）直接判断并填写：不论α取何值，四边形ABCD 的形状一定是________；（2）①当点B 为(1)p ，时，四边形ABCD 是矩形，试求p α、和m 的值； C B DBAB BE B（第23题图）②观察猜想：对①．中．的m 值，能使四边形ABCD 为矩形的点B 共有．．几个？（不必说理） （3）试探究：四边形ABCD 能不能是菱形？若能，直接写出B 点的坐标；若不能，说明 理由.26.（14分）如图所示，在同一直角坐标系中，已知抛物线214y x x k =-+与y 轴相交于点 (01)B ，，点()C m n ，在该抛物线上，且以BC 为直径的O ⊙恰好．．经过顶点A . （1）求k 的值；（2）求点C 的坐标；（3）若点P 的纵坐标为t ，且点P 在该抛物线的对称轴l 上运动，试探索：①当12S S S <<时，求t 的取值范围（其中：S 为PAB △的面积，1S 为OAB △的面积， 2S 为四边形OACB 的面积）； ②当t 取何值时，点P 是对称轴l 与M ⊙的交点.（只要写出t 的值即可）四、附加题（共10分）：在答题卡上相应题目的答题区域内作答.友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况.如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷总分已经达到或超过90分，则本题的得分不计入全卷总分. 填空：1.（5分）计算：23x x -=_______________.2.（5分）如图，在ABC △中，2BC =，则中位线DE =___________.x y （第26题图） O A B B AEBDBBBCBDBxyO（第25题图）A CBB y3y =2010年福建省泉州市初中毕业、升学考试数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分． （三）以下解答各行右端所注分数表示正确做完该步应得的累计分数． 一、选择题（每小题3分，共21分）1．C ； 2．C ； 3．A ； 4．B ； 5．A ； 6．D ； 7．D ． 二、填空题（每小题4分，共40分） 8．4x =-； 9．51.0110⨯； 10．360； 11．45；12．65°；13．90°；14．1；15．增大，3；16．7、6、3（或7、6、2）17．弦AB 的长为43； 三、解答题（共89分） 18．（本小题满分9分）解：原式13142=+⨯ ·························································································· （7分） 422=-+ ························································································································ （8分）4=． ································································································································ （9分）19．（本小题满分9分）解：原式2321x x x =-+-= ···························································································· （4分）31x =-； ························································································································· （5分）当2x =-时，原式=3(2)1-- ·························································································· （7分）81=-- ···························································································································· （8分） 9=-． ······························································································································ （9分）20．（本小题满分9分） 解：（1）5500.12a b c ===，，； ············································································· （3分）····················································· （6分）（2）成绩在69.5~79.5范围内的扇形的圆心角的度数为36020%72⨯=°°．············· （9分） 21．（本小题满分9分） （1）证明：在正方形ABCD 中， 90D ABC AD AB ∠=∠==°，， ··································· （1分） 90ABF D ABF ∴∠=∴∠=∠°，， ·································· （3分） 又DE BF =， ···································································· （4分） ADE ABF ∴△≌△； ······················································ （5分） （2）将ADE △顺时针旋转90度后与ABF △重合， ·················································· （7分） 旋转中心是A 点． ············································································································ （9分） 22．（本小题满分9分） 解：（1）摸出白球的概率是12（或0.5）； ······································································ （4分） （2）列举所有等可能的结果，画树状图：····················· （8分） 两次都摸出白球的概率为：41()164P ==两白．······························································· （9分） （解法二）列表如下：（略）23．（本小题满分9分）解：如图，在Rt DAE △中，90456A AED DE ∠=∠==°，°，， cos AEAED DE∠=， ························································· （2分）cos AE DE AED ∴=⨯∠ 6cos 45=⨯° ········································································ （3分）6=·························································································································· （4分）= ··························································································································· （5分）BE AB AE =-， ········································································································· （6分）BE ∴== ························································································· （7分）在Rt BCE △中，7sin BEEC BCE CE=∠=，·································································· （8分）=·························································································································· （9分） A D CB EFA BC DE24．（本小题满分9分）解：（1）···································································（4分）（2）由（1）得：1560008000100000x yx y+=⎧⎨+=⎩······························································（6分）解得：105xy=⎧⎨=⎩；··············································································································（8分）5108570∴⨯+⨯=．答：这批蔬菜共有70吨． ·······························································································（9分）25．（本小题满分12分）解：（1）平行四边形．·····································································································（3分）（2）①点(1)B p，在y=的图象上，1p∴=p∴ ···························································（4分）过B作BE x⊥轴于E，则OE=1BE=，在Rt BOE△中，tanBEOEα===．30α∴=°． ·····················································································································（5分）2OB∴=．又点B、D是正比例函数与反比例函数图象的交点，∴点B、D关于原点O成中心对称．············································································（6分）2OB OD∴==．四边形ABCD是矩形，(0)(0)A m C m-，，，，2OA OB OC OD∴====．·······················································································（7分）2m∴=；·························································································································（8分）②能使四边形ABCD为矩形的点B共有2个；·····························································（9分）（3）四边形ABCD不能是菱形． ················································································（10分）法一：点A、C的坐标分别为(0)m-，、(0)m，，∴四边形ABCD的对角线AC在x轴上．···································································（11分）又点B、D分别是正比例函数与反比例函数在第一、三象限的交点．∴对角线AC与BD不可能垂直．∴四边形ABCD 不能是菱形． ······················································································ （12分） 法二：若四边形ABCD 为菱形，则对角线AC BD ⊥，且AC 与BD 互相平分，因为点A 、C 的坐标分别为(0)m -，、(0)m ，， 所以点A 、C 关于原点O 对称，且AC 在x 轴上． ···················································· （11分） 所以BD 应在y 轴上，这与“点B 、D 分别在第一、三象限”矛盾，所以四边形ABCD 不能是菱形． ·················································································· （12分）26．（本小题满分14分） 解：（1）点(01)B ，在214y x x k =-+的图象上， 211004k ∴=⨯-+ ················································· （2分）1k ∴=． ································································· （3分）（2）由（1）知抛物线为：2114y x x =-+即21(2)4y x =-，∴顶点A 为(20)，． ················· （4分）21OA OB ∴==，．过点()C m n ，作CD x ⊥轴于D ，则2CD n OD m AD m ==∴=-，，． 以BC 为直径的M ⊙过点A ，90BAC ∴∠=°， ············································································································ （5分） 90CAD BAO ∴∠+∠=°．又90BAO OBA ∠+∠=°， OBA CAD ∴∠=∠，Rt Rt OAB DCA ∴△∽△，AD CD OB OA ∴=，212m n-∴=． ······················································································ （6分） （或tan tan OBA CAD ∠=∠，212OA CD nOB AD m =∴=-，． ······································ （6分）） 2(2)n m ∴=-；又点()C m n ，在21(2)4y x =-的图象上，21(2)4n m ∴=-， 212(2)(2)4m m ∴-=-，即8(2)(10)02m m m --=∴=，或10m =； 当2m =时，0n =，当10m =时，16n =；······························································· （7分）∴符合条件的点C 的坐标为(20)，或(1016)，． ······························································ （8分） （3）①依题意得，点(20)C ，不符合条件，∴点C 为(1016)，． 此时1112S OA OB =⨯=，221ACD BODC S S S =-=△梯形， ··········································· （9分） yx2x =16PBO CD10 A 2。

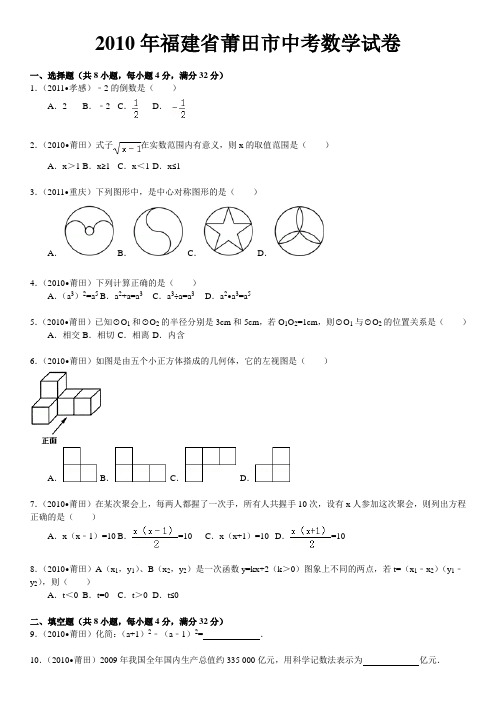
2010年福建省莆田市中考数学试卷一、选择题（共8小题，每小题4分，满分32分）1．（2011•孝感）﹣2的倒数是（）A．2 B．﹣2 C．D．2．（2010•莆田）式子在实数范围内有意义，则x的取值范围是（）A．x＞1 B．x≥1 C．x＜1 D．x≤13．（2011•重庆）下列图形中，是中心对称图形的是（）A．B．C．D．4．（2010•莆田）下列计算正确的是（）A．（a3）2=a5 B．a2+a=a3C．a3÷a=a3D．a2•a3=a55．（2010•莆田）已知⊙O1和⊙O2的半径分别是3cm和5cm，若O1O2=1cm，则⊙O1与⊙O2的位置关系是（）A．相交 B．相切 C．相离 D．内含6．（2010•莆田）如图是由五个小正方体搭成的几何体，它的左视图是（）A． B．C．D．7．（2010•莆田）在某次聚会上，每两人都握了一次手，所有人共握手10次，设有x人参加这次聚会，则列出方程正确的是（）A．x（x﹣1）=10 B．=10 C．x（x+1）=10 D．=108．（2010•莆田）A（x1，y1）、B（x2，y2）是一次函数y=kx+2（k＞0）图象上不同的两点，若t=（x1﹣x2）（y1﹣y2），则（）A．t＜0 B．t=0 C．t＞0 D．t≤0二、填空题（共8小题，每小题4分，满分32分）9．（2010•莆田）化简：（a+1）2﹣（a﹣1）2=_________．10．（2010•莆田）2009年我国全年国内生产总值约335 000亿元，用科学记数法表示为_________亿元．11．（2010•莆田）如图，D、E分别是△ABC边AB、AC的中点，BC=10，则DE=_________．12．（2010•莆田）一个n边形的内角和是720°，则n=_________．13．（2010•莆田）已知数据：1，3，2，x，2的平均数是3，则这组数据的众数是_________．14．（2010•莆田）如果关于x的方程x2﹣2x+a=0有两个相等的实数根，那么a=_________．15．（2010•莆田）若用半径为20cm，圆心角为240°的扇形铁皮，卷成一个圆锥容器的侧面（接缝忽略不计），则这个圆锥容器的底面半径是_________cm．16．（2010•莆田）某同学利用描点法画二次函数y=ax2+bx+c（a≠0）的图象时，列出的部分数据如下表：经检查，发现表格中恰好有一组数据计算错误，请你根据上述信息写出该二次函数的解析式：_________．三、解答题（共9小题，满分86分）17．（2010•莆田）计算：|﹣2|+﹣22．18．（2010•莆田）解不等式，并把它的解集在数轴上表示出来．19．如图，四边形ABCD的对角线AC、DB相交于点O，现给出如下三个条件：①AB=DC；②AC=DB；③∠OBC=∠OCB．（1）请你再增加一个_________条件使得四边形ABCD为矩形（不添加其它字母和辅助线，只填一个即可，不必证明）；（2）请你从①②③中选择两个条件_________（用序号表示，只填一种情况），使得△AOB≌△DOC，并加以证明．20．（2010•莆田）如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，点A、B的坐标分别为A（﹣2，3）、B（﹣3，1）．（1）画出坐标轴，画出△AOB绕点O顺时针旋转90°后的△A1OB1；（2）点A1的坐标为_________；（3）四边形AOA1B1的面积为_________．21．（2010•莆田）如图，A、B是⊙O上的两点，∠AOB=120°，点D为劣弧的中点．（1）求证：四边形AOBD是菱形；（2）延长线段BO至点P，交⊙O于另一点C，且BP=3OB，求证：AP是的⊙O切线．22．（2010•莆田）在一个不透明的盒子里，装有四个分别标有数字1，2，3，4的小球，它们的形状、大小、质地等完全相同．小明先从盒子里随机取出一个小球，记下数字为x；放回盒子摇匀后，再由小华随机取出一个小球，记下数字为y．（1）用列表法表示出（x，y）的所有可能出现的结果；（2）求小明、小华各取一次小球所确定的点（x，y）落在反比例函数y=的图象上的概率；（3）求小明、小华各取一次小球所确定的数x，y满足y＜的概率．23．（2010•莆田）一方有难，八方支援．2010年4月14日青海玉树发生地震，全国各地积极运送物资支援灾区．现有甲、乙两车要从M地沿同一公路运输救援物资往玉树灾区的N地，乙车比甲车先行1小时，设甲车与乙车之间的路程为y（km），甲车行驶的时间为t（h），y（km）与t（h）之间的函数关系的图象如图所示．结合图象解答下列问题（假设甲、乙两车的速度始终保持不变）：（1）乙车的速度是_________km/h；（2）求甲车的速度和a的值．24．（2010•莆田）如图1，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D在边AB上运动，DE平分∠CDB交边BC于点E，EM⊥BD垂足为M，EN⊥CD垂足为N．（1）当AD=CD时，求证：DE∥AC；（2）探究：AD为何值时，△BME与△CNE相似？（3）探究：AD为何值时，四边形MEND与△BDE的面积相等？25．（2010•莆田）如图1，在平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=1，OC=2，点D在边OC上且OD=．（1）求直线AC的解析式；（2）在y轴上是否存在点P，直线PD与矩形对角线AC交于点M，使得△DMC为等腰三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．（3）抛物线y=﹣x2经过怎样平移，才能使得平移后的抛物线过点D和点E（点E在y轴的正半轴上），且△ODE 沿DE折叠后点O落在边AB上O′处．2010年福建省莆田市中考数学试卷参考答案与试题解析一、选择题（共8小题，每小题4分，满分32分）1．（2011•孝感）﹣2的倒数是（）A．2 B．﹣2 C．D．考点：倒数。

2010年宁德市初中毕业、升学考试数学试题（全卷共6页，三大题，共26小题；满分150分；考试时间120分钟）友情提所有答案都必须填涂在答题卡上，答在本试卷上无2B铅笔在答题卡的相应位置填涂）《国家中长期教育改革和发展规划纲要》中指出，“加大教育投入.提高国家财政性教育经费支出占国内生产总值比例，2012年达到4% . ”如果2012年我国国内生产总值为435000亿元，那么2012年国家财政性教育经费支出应为（结果用科学记数法表示）（）.参考公式：抛物线y = ax2bx • c a = 0的顶点是b 4ac「b22a' 4a，对称轴是直线x -i 2a、选择题（本大题有10小题，每小题4分, 满分40分.每小题只有一个正确的选项，请1.1的相反数是（3 )•A.3B.-C.-3D.2.3如图所示几何体的俯视图是（A. D.3. F列运算中，结果正确的是（A. a a =a2B. a2a2二a43\2C.(a ) a5D. a3 a3二a4. F列事件是必然事件的是（).A.随意掷两个均匀的骰子，朝上面的点数之和为B.抛一枚硬币，正面朝上C.3个人分成两组，一定有2个人分在一组D.打开电视，正在播放动画片5.如图，在O O中，/ ACB = 34°，则/ AOB的度数是（).A.17 °B.34 °C.56 °D.68°6.今年颁布的).C.A.4.35 X 10 亿元B.1.74 X 10 亿元C.1.74 X 10 亿元D. 174 X 10 亿元9.如图，在8X 4的方格（每个方格的边长为1个单位长）中，O A的半径为1 , O B的半径为2,将O A由图示位置向右平移1个单位长后, O A与静止的O B的位置关系是（）.A.内含B.内切C.相交D.外切10•如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个直角三角形，展开后得到一个等腰三角形•则展开后三角形的周长是（8小题，每小题3分，满分24分•请将答案用黑色签字笔填入答题卡的相应位置）2 212. 分解因式：ax + 2axy + ay =13. 如图，把一块直角三角板的直角顶点放在直尺的一边上，如果/ 仁35°那么/ 2是________ °.14. 如图，在△ ABC中，点E、F分别为AB、AC的中点.若EF的长为2,则BC的长为____________ .15. 下表是中国2010年上海世博会官方网站公布的5月某一周入园参观人数,A. B. C. D.&反比例函数1y (x> 0)x的图象如图所示，随着x值的增大，y值（A •减小B .增大C.不变 D .先减小后不变日期22日23日24日25日26日27日28日入园人数（万）36.1231.1431.434.4235.2637.738.12则这一周入园参观人数的平均数是_____________ 万.16.如图，在口ABCD中, AE= EB, AF= 2，贝U FC 等于____D第16题图10A . 2+ 10B. 2 + 2 . 10C. 12 1811.化简:a ba —b a —b、填空题（本大题有F第14题图17. 如图，在直径 AB = 12的O O 中，弦CD 丄AB 于M ，且M 是半径 0B 的中点, 则弦CD 的长是 ________ （结果保留根号） 18.用m 根火柴可以拼成如图1所示的x 个正方形，还可以拼成如图2所示的第18题图三、解答题（本大题有8小题，满分86分.请将解答过程用黑色签字笔写在答题卡的相应位置. 作图或添辅助线用铅笔画完，再用黑色签字笔描黑） 19. （每小题7分，满分14分）⑴化简：（a + 2） （a — 2）— a （a + 1）;2x —1 5x +1⑵ 解不等式 竺」＜ 1，并把它的解集在数轴上表示出来.3 2-5 -4 -3 -2 -10 123 4 520. （本题满分8分）如图，已知AD 是厶ABC 的角平分线，在不添加任何辅助线的前提下,21. （本题满分8分）某校九年级（1 ）班所有学生参加 2010年初中毕业生升学体育测试,条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题:2y 个正方形，那么用含 x 的代数式表示y ，得y = 要使△ AED ^A AFD ，需添加一个条件是:根据测试评分标准，将他们的成绩进行统计后分为A B C 、D 四等，并绘制成如图所示的第17题图1）班体育测试成绩统计图⑴ 九年级（1）班参加体育测试的学生有_____________ 人；⑵ 将条形统计图补充完整；⑶ 在扇形统计图中，等级B部分所占的百分比是—，等级C对应的圆心角的度数为—°⑷若该校九年级学生共有850人参加体育测试，估计达到A级和B级的学生共有—人.22. （本题满分8分）我们知道当人的视线与物体表面互相垂直时的视觉效果最佳•如图是小明站在距离墙壁 1.60米处观察装饰画时的示意图，此时小明的眼睛与装饰画底部A处于同一水平线上，视线恰好落在装饰画中心位置E处，且与AD垂直.已知装饰画的高度AD为0.66 米，求：⑴装饰画与墙壁的夹角/ CAD的度数（精确到1 °）;⑵装饰画顶部到墙壁的距离DC （精确到0.01米）.23. （本题满分10分）据宁德网报道：第三届海峡两岸茶业博览会在宁德市的成功举办，提升了闽东茶叶的国内外知名度和市场竞争力，今年第一季茶青（刚采摘下的茶叶）每千克的价格是去年同期价格的10倍.茶农叶亮亮今年种植的茶树受霜冻影响，第一季茶青产量为198.6千克，比去年同期减少了87.4千克，但销售收入却比去年同期增加8500元.求茶农叶亮亮今年第一季茶青的销售收入为多少元？1 2 124. （本题满分12分）如图1，抛物线y X X与x轴交于A、C两点，与y轴4 4交于B点，与直线y = kx • b交于A D两点。

初中毕业生学业考试数 学 试 卷※考试时间120分钟 试卷满分150分一、选择题（下列各题的备选答案中，只有一个是正确的，请将正确答案的选项填在下表中相应题号下的空格内．每小题3分，共24分）1．目前国内规划中的第一高楼上海中心大厦，总投入约14 800 000 000元．14 800 000 000元用科学记数法表示为（ ） A ．111.4810⨯元B ．90.14810⨯元C ．101.4810⨯元D ．914.810⨯元2．计算23(2)a -的结果为（ ） A ．52a -B ．68a -C ．58a -D ．66a -3．如图所示，已知直线AB CD ∥，125C ∠=°，45A ∠=°， 则E ∠的度数为（ ） A ．70° B ．80° C ．90° D ．100°4．一个圆柱体钢块，正中央被挖去了一个长方体孔，其俯视图如图所示，则此圆柱体钢块的左．视图是（ ）5．数据21，21，21，25，26，27的众数、中位数分别是（ ） A ．21，23 B ．21，21 C ．23，21 D ．21，256．为了美化环境，某市加大对绿化的投资．2007年用于绿化投资20万元，2009年用于绿化投资25万元，求这两年绿化投资的年平均增长率．设这两年绿化投资的年平均增长率为x ，根据题意所列方程为（ ） A ．22025x =B ．20(1)25x +=C ．220(1)25x +=D ．220(1)20(1)25x x +++=7．如图所示，反比例函数1y 与正比例函数2y 的图象的一个交点坐标是(21)A ，，若210y y >>，则x 的取值范围在数轴上表示为（ ）A ．B ．C ．D ． 俯视图第4题图 EA BCD第3题图45°125°8．将一等腰直角三角形纸片对折后再对折，得到如图所示的图形，然后将阴影部分剪掉，把剩余部分展开后的平面图形是（ ）二、填空题（每小题3分，共24分） 9．分解因式：34a a -= ． 10．函数33y x =+自变量x 的取值范围是 ． 11．小丽想用一张半径为5cm 的扇形纸片围成一个底面半径为4cm 的圆锥，接缝忽略不计，则扇形纸片的面积是 cm 2．（结果用π表示）12．如图所示，小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分，阴影部分是黑色石子，小华随意向其内部抛一个小球，则小球落在黑色石子区域内的概率是 ． 13．如图所示，AB 为O ⊙的直径，P 点为其半圆上一点，40POA C ∠=°，为另一半圆上任意一点（不含A B 、），则PCB ∠= 度．14．已知抛物线（）经过点，且顶点在第一象限．有下列三个结论：①0a < ②0a b c ++> ③02ba->．把正确结论的序号填在横线上 ．15．如图所示，在正方形网格中，图①经过 变换（填“平移”或“旋转”或“轴对称”）可以得到图②；图③是由图②经过旋转变换得到的，其旋转中心是点 （填“A ”或“B ”或“C ”）． 16．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n 个图形需要黑色棋子的个数是 ．A ．B ．C ．D ．y 1 2 2 1 1- (21)A ， y 2 y 1 x O垂直 A ． B ． C ． D ． 第8题图 第12题图 CB A P O 40° 第13题图O y x 第14题图1- ①② ③ 第15题图A B C三、解答题（每题8分，共16分）17．计算：012|32|(2π)+-+-．18．解方程：2111x x x -=-+．四、解答题（每题10分，共20分）19．如图所示，在Rt ABC △中，9030C A ∠=∠=°，°．（1）尺规作图：作线段AB 的垂直平分线l （保留作图痕迹，不写作法）；（2）在已作的图形中，若l 分别交AB AC 、及BC 的延长线于点D E F 、、，连接BE ． 求证：2EF DE =．20．某市开展了党员干部“一帮一扶贫”活动．为了解贫困群众对帮扶情况的满意程度，有关部门在该市所管辖的两个区内，分别随机抽取了若干名贫困群众进行问卷调查．根据收集的信息进行了统计，并绘制了下面尚不完整的统计图．已知在甲区所调查的贫困群众中，非常满意的人数占甲区所调查的总人数的35%．根据统计图所提供的信息解答下列问题： （1）甲区参加问卷调查的贫困群众有 人； （2）请将统计图补充完整； （3）小红说：“因为甲区有30人不满意，乙区有40人不满意，所以甲区的不满意率比乙区低．”你认为这种说法正确吗？为什么？第1个图形 第2个图形 第3个图形 第4个图形第16题图A CB 第19题图 非常满意 人数 800 600 400 200 满意 比较满意 不满意 满意程度 甲 乙第20题图420 700 760500250 3040五、解答题（每题10分，共20分）21．小明和小亮是一对双胞胎，他们的爸爸买了两套不同品牌的运动服送给他们，小明和小亮都想先挑选．于是小明设计了如下游戏来决定谁先挑选．游戏规则是：在一个不透明的袋子里装有除数字以外其它均相同的4个小球，上面分别标有数字1、2、3、4．一人先从袋中随机摸出一个小球，另一人再从袋中剩下的3个小球中随机摸出一个小球．若摸出的两个小球上的数字和为奇数，则小明先挑选；否则小亮先挑选． （1）用树状图或列表法求出小明先挑选的概率； （2）你认为这个游戏公平吗？请说明理由．22．如图所示，已知AB 是半圆O 的直径，弦106CD AB AB CD ==∥，，，E 是AB 延长线上一点，103BE =．判断直线DE 与半圆O 的位置关系，并证明你的结论．六、解答题（每题10分，共20分）23．某旅游区有一个景观奇异的望天洞，D 点是洞的入口，游人从入口进洞游览后，可经山洞到达山顶的出口凉亭A 处观看旅游区风景，最后坐缆车沿索道AB 返回山脚下的B 处．在同一平面内，若测得斜坡BD 的长为100米，坡角10DBC ∠=°，在B 处测得A 的仰角40ABC ∠=°，在D 处测得A 的仰角85ADF ∠=°，过D 点作地面BE 的垂线，垂足为C ．（1）求ADB ∠的度数； （2）求索道AB 的长．（结果保留根号）O AB ED C 第22题图A C DE F B 第23题图24．为迎接国庆六十周年，某校团委组织了“歌唱祖国”有奖征文活动，并设立了一、二、三等奖．学校计划派人根据设奖情况买50件奖品，其中二等奖件数比一等奖件数的2倍还少10件，三等奖所花钱数不超过二等奖所花钱数的1.5倍．各种奖品的单价如下表所示．如果计划一等奖买x 件，买50件奖品的总钱数是w 元． （1）求w 与x 的函数关系式及自变量x 的取值范围； （2）请你计算一下，如果购买这三种奖品所花的总钱数最少？最少是多少元？一等奖 二等奖 三等奖 单价(元) 12 10 5 E图（b ） 第25题图八、解答题（本题14分）26．如图所示，已知在直角梯形OABC 中，AB OC BC x ∥，⊥轴于点(11)(31)C A B ，，、，．动点P 从O 点出发，沿x 轴正方向以每秒1个单位长度的速度移动．过P 点作PQ 垂直于直线．．OA ，垂足为Q ．设P 点移动的时间为t 秒（04t <<），OPQ △与直角梯形OABC 重叠部分的面积为S ．（1）求经过O A B 、、三点的抛物线解析式； （2）求S 与t 的函数关系式；2009年铁岭市初中毕业生学业考试 数学试题参考答案及评分标准注：本参考答案只给出一种或几种解法（证法），若用其他方法解答并正确，可参考此评分标准相应步骤赋分．一、选择题（每小题3分，共24分） 题号 1 2 3 4 5 6 7 8 答案 C B B C A C D A∴3060EBA A AED BED ∠=∠=∠=∠=°，°，∴3060EBC EBA FEC ∠==∠∠=°，°． 又∵ED AB EC BC ⊥，⊥， ∴ED EC =． ······························································································· 8分 在Rt ECF △中，6030FEC EFC ∠=∴∠=°，°， ∴2EF EC =， ∴2EF ED =． ··························································································· 10分 第19题图（2）图形正确（甲区满意人数有500人） ··························································· 5分 （3）不正确． ······························································································· 6分 ∵甲区的不满意率是30 2.5%1200=，乙区的不满意率是402%70076050040=+++， ∴甲区的不满意率比乙区的不满意率高． ·························································· 10分五、（每题10分，共20分） 21．解：（1）根据题意可列表或树状图如下：第一次第二次1 2 3 4∵，∴2．······························· 2分 ∵1025533OE OB BE =+=+=． ····························· 3分 ∴35325553DF OD OD OE ===，， ∴DF ODOD OE=． ····························································································· 6分 ∵CD AB ∥，∴CDO DOE ∠=∠． ································································ 7分3） A第22题图∴90ODE OFD ∠=∠=°， ∴OD DE ⊥∴直线DE 与半圆O 相切． ············································································ 10分 法二：连接OD ，作OF CD ⊥于点F ，作DG OE ⊥于点G ． ∵6CD =，∴132DF CD ==． 在Rt ODF △中，2222534OF OD DF =-=-= ·········································· 3分 ∵CD AB ∥，DG AB OF CD ⊥，⊥， ∴四边形OFDG 是矩形，∴43DG OF OG DF ====，． ∵1025533OE OB BE =+=+=，2516333GE OE OG =-=-=， ························ 5分 在Rt DGE △中，22221620433DE DG GE ⎛⎫=+=+= ⎪⎝⎭．∵2222025533⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭， ∴222OD DE OE += ····················································································· 8分 ∴CD DE ⊥．∴直线DE 与半圆O 相切． ············································································ 10分 六、（每题10分，共20分） 23．（1）解：∵DC CE ⊥，∴90BCD ∠=°． 又∵10DBC ∠=°， ∴80BDC ∠=°， ····················································· 1分∵85ADF ∠=°，∴360809085105ADB ∠=---=°°°°°． ·················· 2分（2）过点D 作DG AB ⊥于点G ． ······························ 3分 在Rt GDB △中，401030GBD ∠=-=°°°， ∴903060BDG ∠=-=︒°° ········································ 4分 又∵100BD =， ∴111005022GD BD ==⨯=． 3cos301005032GB BD ==⨯=°． ···························································· 6分 在Rt ADG △中，1056045GDA ∠=-=︒°° ······················································ 7分 ∴50GD GA ==， ························································································ 8分 ∴50503AB AG GB =+=+（米）································································ 9分A CDEF B 第23题图G答：索道长50+ ············································································· 10分 24．解：（1）1210(210)5[50(210)]x x x x ω=+-+--- ····································· 2分17200x =+．·········································································· 3分 由02100[50(210)]05[50(210)] 1.510(210)x x x x x x x >⎧⎪->⎪⎨--->⎪⎪---⨯-⎩≤ ························································ 5分（3）当CD CB =（2BD CD =或12CD BD =或30CAD ∠=°或90BAD ∠=°或30ADC ∠=°）时，四边形BCGE 是菱形． ················ 9分 理由：法一：由①得AEB ADC △≌△， ∴BE CD = ························································· 10分 又∵CD CB =， ∴BE CB =． ······················································ 11分 由②得四边形BCGE 是平行四边形， ∴四边形BCGE 是菱形． ······································· 12分ADCBFEG 图（b ） 第25题图法二：由①得AEB ADC △≌△， ∴BE CD =． ······························································································ 9分 又∵四边形BCGE 是菱形， ∴BE CB = ································································································ 11分 ∴CD CB =． ····························································································· 12分 法三：∵四边形BCGE 是平行四边形， ∴BE CG EG BC ∥，∥， ∴6060FBE BAC F ABC ∠=∠=∠=∠=°，° ··················································· 9分 ∴60F FBE ∠=∠=°， ∴BEF △是等边三角形． ············································································· 10分220(02)1(12)a h a h ⎧=-+⎪⎨=-+⎪⎩ 解得1343a h ⎧=-⎪⎪⎨⎪=⎪⎩································································· 3分 ∴所求抛物线解析式为214(2)33y x x =--+． ···················································· 4分 （2）分三种情况：①当02t <≤，重叠部分的面积是OPQ S △，过点A 作AF x ⊥轴于点F ， ∵(11)A ，，在Rt OAF △中，1AF OF ==，45AOF ∠=°在Rt OPQ △中，OP t =，45OPQ QOP ∠=∠=°，∴cos 452PQ OQ t ===°， （3）存在 11t = ······················································································ 12分 22t = ···················································································· 14分。

厦门市海沧区初中毕业班质量检查数学 试 题（试卷满分：１50分，考试时间：120分钟）考生注意：1、 解答的内容一律写在答题卡上，否则以0分计算2、 可以直接使用0.5毫米的黑色签字笔或2B 铅笔作图或画辅助线.一、选择题：（每题3分，共21分）1．－2的相反数是A ．2B ．－2C ．21D ．－21 2．右图是某几何体的三种视图，则该几何体是 A ．正方体 B ．圆锥体 C ．圆柱体D ．球体3．下列运算正确的是A ．x 2 + x 3 = x 5B ．－2x ·x 2 =－2x 3C ．x 6÷x 2= x 3D ．(－ x 2 )3 = x 64. 如图1，在直角△ABC 中，∠C ＝90°,若BC ＝3，AC ＝4，则tan B ＝( ) A. 35 B. 45 C. 34 D. 43５．下列说法正确的是A. 掷一枚均匀的正方体骰子，骰子停止后朝上的点数是3B. 一组数据2，3，3，6，8，5的中位数是５C.. “打开电视，正在播广告”是必然事件D ．若Ａ、Ｂ两组数据的方差分别是ＳＡ＝0.21、ＳＢ＝0.02，则Ｂ组数据比Ａ组数据稳定 6．若多项式241x a ++是一个完全平方式，则a 的值不正确的是（ ） A. 4x B. －4x C. 44x D. 2x 7．如图，是一次函数y =kx +b 与二次函数y =2312x x --的图像， 则关于x 的方程kx +b =2312x x --的解为（ ） A ．x l ＝－1，x 2＝2 B ．x l ＝1，x 2＝-2 C ．x l ＝0，x 2＝2 D ．x l ＝0，x 2＝-2主视图俯视图 左视图图 1CBA二、填空题：（每题4分，共40分）8．计算：2-＝ ；9．据悉，上海世博会将有7000万人参观，其规模和影响将是历史之最。

用科学记数法表示“7000万人”的结果是：人 10．方程组2420x y x y +=⎧⎨-=⎩的解是 ．11．一名警察在高速公路上随机观察了6辆车的车速，如下表所示：则这6辆车车速的众数是 千米/时.12．等腰三角形的两边长分别为10、12，则它的周长为 13. 已知cos 2θ=，且θ为锐角，则sin θ＝ 14. 抛物线y= x 2＋2x 的顶点坐标是 .15．如图，ABC △内接于⊙O ，AD 是⊙O 的直径，25ABC ∠=，则CAD ∠=°．16．已知如图，在ABC △中，AD ⊥BC ，中位线EF ＝5，AD ＝8，则ABC △的面积是. 17．如图，把一个矩形纸片OABC 放入平面直角坐标系中，使OA 、OC 分别落在x 轴、y 轴上，连结OB ，将纸片OABC 沿OB 折叠，使点A 落在A '的位置上．若OB=5，21=OC BC ，求点A '的坐标为_______________．BC第15题 第16题 三、解答题（9大题，共89分） 18、（1）计算（6分）：12012222--+-+ ； （2）计算（6分）：)3)(3()3(-++-x x x x ；D(3) 解方程（6分）：11322x x x --=-- ； 19．（本题满分8分）甲乙两同学参加创建全国文明城市知识竞赛，其中有4道不同的题目，题号为1，2的是选择题，题号为3，4的是，甲、乙先后各随机抽取一题（抽后均不放回） （1）用画树状图的方法列举所有可能的抽题情况；（2）求事件“甲、乙两人抽到相同题型(即都是选择题或都是判断题)”的概率P ； 20．（本题满分8分）如图，正方形ＡＢＣＤ的边长为E 是边AD 上的一个动点（不与Ａ重合），ＢＥ交对角线于Ｆ，连结ＤＦ． ⑴ 求证：ＢＦ＝ＤＦ⑵ 设ＡＦ＝ｘ，△ＡＢＦ面积为ｙ，求ｙ与ｘ的函数关系式，并画出图象．21. （本题满分8分）如图，在路边O 处安装路灯，路面宽ED 为16米，灯柱OB 与灯杆AB 成120°角．灯柱OB 与路面ED 垂直（OB ⊥OD ），路灯A 采用锥形灯罩，灯罩轴线AC 与灯杆AB 垂直，并与路面ED 交于点C ，AE 恰好与OD 垂直．当路灯A 到路面的距离AE 为多少米时，点C 正好是路面ED 的中点？22．（本题满分8分）在某次数字变换游戏中，我们把整数0，1，2，…，100称为“旧数”，游戏的变换规则是：将旧数先平方，再除以100，所得到的数称为“新数”． 例如：旧数26的新数为262÷100＝6.76（1）经过上述规则变换后，有人断言：“按照上述变换规则，所有的新数都小于它的旧数．”你认为这种说法对吗？请说明理由，若不对，请举一反例说明.（2）请求出按照上述规则变换后减小了最多的旧数（要写出解答过程）． 23. （本题满分8分）如图，AB 为半圆O 的直径，点C 在半圆O 上，过点O 作BC 的 平行线交AC 于点E ，交过点A 的直线于点D ，且∠D=∠BAC. 1） （4分）求证：AD 是⊙O 的切线；2） （4分）若BC=2，AD 的长.A B OCDE120°A BO CDE BACE2４. （本题满分9分） 已知关于x 的方程()()2322200mxm x m m -+++=⑴ 求证：方程有两个不相等的实数根.⑵ 设此方程的两个实数根分别是,a b （其中a ＜b ）.若2y b a =-，求满足2y m =的m 的值 . 25.（本题满分10分）在△ABC 中，∠ACB 为锐角，动点D （异于点B ）在射线BC 上，连接AD ，以AD 为边在AD 的右侧作正方形ADEF ，连接CF.⑴ 若AB=AC ，∠BAC=90°那么① 如图一，当点D 在线段BC 上时，线段CF 与BD 之间的位置、大小关系是（直接写出结论）② 如图二，当点D 在线段BC 的延长上时，①中的结论是否仍然成立？请说明理由.⑵ 若AB ≠AC ，∠BAC ≠90°。

二0一0年福州市初中毕业会考、高级中等学校招生考试数学试卷（全卷共4页，三大题，共22小题，满分150分，考试时间120分钟）友情提示：所有答案都必须填涂在答题卡相应的位置上，答在本卷上一律无效。

毕业学校 姓名 考生号一、选择题（共10小题，每题4分，满分40分；每小题只有一个正确的选项，请在答题卡的相应位置填涂） 1．2的倒数是A.12 B. 12- C. 2 D.－2 2. 今年我省规划重建校舍约3890000平方米，3890000用科学记数法表示为A. 70.38910⨯ B. 63.8910⨯ C. 43.8910⨯ D. 438910⨯ 3.下面四个图形中，能判断∠1 > ∠2的是4.下面四个中文艺术字中，不是．．轴对称图形的是5.x 的取值范围为 A. 1x ≠ B.1x ≥ C.1x < D.全体实数6.下面四个立体图形中，主视图是三角形的是7.已知反比例函数ky x=的图像过点P （1，3），则反比例函数图像位于 A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限8. 有人预测2010年南非世界杯足球赛巴西国家队夺冠的概率是70%他们的理解正确的是A.巴西国家队一定夺冠B.巴西国家队一定不会夺冠C.巴西国家队夺冠的可能性比较大D.巴西国家队夺冠的可能性比较小 9.分式方程312x =-的解是 A. 5x = B. 1x = C. 1x =- D. 2x =10.已知二次函数2y ax bx c =++的图像如图所示，则下列结论正确的是A.0a >B. 0c <C.240b ac -< D.0a b c ++>二、填空题（共5小题，每题4分，满分20分。

请将答案填入答题卡相应的位置） 11.实数a 、b 在数轴上对应点的位置如图所示，则a b （填“>”、“<”或“=”）。

12.因式分解：21x -= 。

13.某校七年（2班）6位女生的体重（单位：千克）是：36，38，40，42，42，45，这组数据的众数为 。

教学资料教育精品资料2010年福建省厦门市中考数学试卷参考答案与试题解析一、选择题（共7小题，每小题3分，满分21分）1．（2010•厦门）下列几个数中，属于无理数的是（）A．B．2 C．0 D．考点：无理数。

专题：应用题。

分析：由于无理数是开不尽方的数，或者无限不循环小数为无理数，由此即可判定选择项．解答：解：2，0，是有理数；开方开不尽故是无理数．故选A．点评：此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，或者无限不循环小数为无理数．如π，，0.…（每两个8之间依次多1个0）等形式．2．（2010•厦门）计算a2•a3的结果是（）A．5a B．a5C．a6D．a8考点：同底数幂的乘法。

专题：计算题。

分析：根据同底数幂的乘法法则，同底数幂相乘，底数不变，指数相加，即a m•a n=a m+n．解答：解：a2•a3=a5．故选B．点评：本题主要考查同底数幂的乘法的性质，熟练掌握性质是解题的关键．3．（2010•厦门）下列四个几何体中，俯视图是圆的几何体共有（）A．1个B．2个C．3个D．4个考点：简单几何体的三视图。

分析：根据俯视图是从上面看所得到的图形判断即可．解答：解：从上面看，长方体的俯视图为长方形；圆柱的俯视图为圆；球的俯视图是圆；三棱柱的俯视图是三角形；俯视图是圆的几何体共有2个，故选B．点评：本题考查了三视图的知识，俯视图是从物体的上面看得到的视图．4．（2010•厦门）在一次数学单元考试中，某小组7名同学的成绩（单位：分）分别是：65，80，70，90，95，100，70．这组数据的中位数是（）A．90 B．85 C．80 D．70考点：中位数。

分析：本题考查统计的有关知识，找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．解答：解：将这组数据按从小到大的顺序排列为：65，70，70，80，90，95，100，处于中间位置的那个数是80，那么由中位数的定义可知，这组数据的中位数是80．故选C．点评：本题为统计题，考查中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．5．（2010•厦门）不等式组的解集为（）A．x＞﹣1 B．x＜2 C．﹣1＜x＜2 D．x＜﹣1或x＞2考点：解一元一次不等式组。