各轴横截面上的最大切应力
- 格式:ppt
- 大小:2.31 MB
- 文档页数:30


最大切应力计算公式在工程力学和材料力学中,最大切应力计算公式可是个相当重要的家伙!咱先来说说啥是切应力。
想象一下,你手里拿着一根铅笔,然后用力把它扭来扭去,铅笔内部产生的那种抵抗你扭转的力,就和切应力有关系。
最大切应力计算公式通常是:τmax = τ = QS/(Ib) 。
这里面的 Q 表示横截面上的剪力,S 是所求应力点到中性轴的距离,I 是横截面对中性轴的惯性矩,b 是截面宽度。
举个例子吧,有一次我去工厂参观,看到工人们在加工一个大型的轴类零件。
那个轴又粗又长,看着就特别结实。
但工程师告诉我,就算这么粗壮的轴,如果所受的切应力超过了材料的承受能力,也会出问题。
当时他们正在计算这个轴在运转时所受到的最大切应力。
工程师们拿着图纸,在上面写写画画,嘴里还念叨着这些公式里的参数。
我凑过去看,发现他们得先准确测量出轴的截面尺寸,确定剪力的大小,然后再代入公式进行计算。
我就好奇地问工程师:“这公式真能算准吗?”工程师笑着说:“这可是经过无数次实验和实践验证的,只要测量数据准确,计算过程不出错,就能得到比较可靠的结果。
”回到最大切应力计算公式,它的应用可广泛啦!比如在机械设计中,要确保零件在工作时不会因为切应力过大而损坏;在建筑结构中,像桥梁的钢梁、支撑柱等,都得靠这个公式来保证其安全性。
再比如说,汽车的传动轴,那可是承受着巨大的扭矩和切应力。
如果不通过最大切应力计算公式来好好设计,说不定开着开着车,传动轴就断了,那得多危险啊!还有飞机的机翼结构,既要轻巧又要能承受各种复杂的力,这时候最大切应力计算公式就派上大用场了,能帮助设计师们找到最合适的材料和结构形式。
总之,最大切应力计算公式虽然看起来有点复杂,但它可是保障各种结构和零件安全可靠的重要工具。
在工程领域,可千万不能小瞧了它的作用!不管是大型的机械设备,还是小小的零件,都得依靠这个公式来确保它们能正常工作,不出现意外。
所以啊,咱们可得好好掌握这个公式,说不定哪天就能派上大用场呢!。


![材料力学习题解答[第三章]](https://uimg.taocdn.com/ad0c511fddccda38376bafaa.webp)
3-1求图中所示杆各个横截面上的应力,已知横截面面积A=400mm 2。
解a):MPaMPa1004001040050400102033231=⨯==-=⨯-=σσσ 题3-1a)图 解b):MPa MPaMPa2540010105050400102032231=⨯=-=-=⨯-=右左σσσ MPa MPa 125400105025333=⨯==右左σσ 题3-1b)图3-2图中为变截面杆,如果横截面面积A 1=200mm 2,A 2=300mm 2,A 3=400mm 2,求杆内各横截面上的应力。
解a ):MPaMPa MPa10040010407.663001020502001010333231=⨯=-=⨯-==⨯=σσσ题3-2a)图解b):MPaMPa 7540010303.333001010033321-=⨯-==⨯==σσσ题3-2b)图30kN3-3 图示杆系结构中,各杆横截面面积相等,即A=30cm 2,载荷F=200kN 。
试求各杆横截面上的应力。
解:(1)约束反力:kNF F kN F F kN F F AXAY Dy 2001504315043======(2)各杆轴力)(250150200)(150)(200)(1502222压压拉拉kN F F F kN F F kN F F kN F F NCD NAC NAC D NCD AX NAC AY NAB =+=+======= 题3-3图(3)各杆的正应力)(3.8330010250,)(5030010150)(7.6630010200,)(50300101503333压压拉拉MPa MPa MPa MPa AC CDAC AB -=⨯-=-=⨯-==⨯==⨯=σσσσ 3-4钢杆CD 直径为20mm ,用来拉住刚性梁AB 。
已知F=10kN ,求钢杆横截面上的正应力。
解:)(7.112204104.3544.3545cos 1)5.11(232拉MPa d F kNF F NCD CD oNCD =⨯⨯===⨯+=ππσ 题3-4图3-5图示结构中,1、2两杆的横截面直径分别为10mm 和20mm ,试求两杆内的应力。
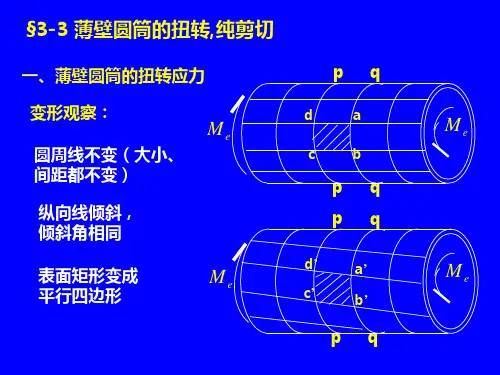

第8章弹性杆件横截面上的切应力分析8-1扭转切应力公式r(p)^M x p/I p的应用范圉有以下几种,试判断哪一种是正确的。
(A)等截面圆轴,弹性范囤内加载:(B)等截面圆轴:(C)等截面圆轴与椭恻轴:(D)等截面圆轴与椭恻轴.弹性范鬧内加较。
知识点:圆轴扭转时横截面上的切应力难度:易解答•正确答案是A cTip) = M x p/l?在推导时利川J'等截面鬪轴受扭后.其横截血保持平血的假设•同时推导过程中还应用了剪切胡克定律.婆求在线弹性范刑加載。
8-2两根长度相等、直径不等的圆轴受扭后.轴表iftlJJU线转过相同的角度。
设直径大的轴和直径小的轴的横截面上的最大切应力分别为耳吨'和r2max,切变模虽分别为Gi和G2O试判断下列结论的正确性。
(A)(B)(C)若G、>G“则有r Inux > r2nux:(D)若G>G“则有右叭沁。
知识点:圆轴扭转时横截面上的切应力难度:易解答•正确答案是c °因两恻轴等长,轴表面上母线转过相同角度,指切应变相同,即/,=/,=/由剪切胡克定律2“知> °2 时,f lnux > r2max °8-3承受相同扭矩且长度相等的直径为山的实心恻轴与内.外径分别为D2(a = d2/D2)的空心圆轴.二者横截面上的垠大切应力相等。
关于二者重之比(M/WJ有如下结论.试判断哪一种是正确的。
(A)(l-a4严;(B)(l-a4)V2(l-a2):(C)(l-^Xl-a2):(D)(1 一a」)的/(I一小)。
知识点:组合圆轴扭转时横截面上的切应力难度:难解答•\6M X I6M正确答案是D即A-d-a4)7D2匹=如=必W2人D;(l-a2)习题8/图⑴代入(2〉.得8-4由两种不同材料组成的圆轴,里层和外 层材料的切变模址分别为Gi 和Gi.且G = 2G 2. 圆轴尺寸如图所示。
圆轴受扭时.里、外层之间无相对滑动。

材料⼒学第五版课后习题答案⼆、轴向拉伸和压缩2-1试求图⽰各杆1-1和2-2横截⾯上的轴⼒,并作轴⼒图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
2-2 试求图⽰等直杆横截⾯1-1,2-2和3-3上的轴⼒,并作轴⼒图。
若横截⾯⾯积,试求各横截⾯上的应⼒。
解:2-3试求图⽰阶梯状直杆横截⾯1-1,2-2和3-3上的轴⼒,并作轴⼒图。
若横截⾯⾯积,,,并求各横截⾯上的应⼒。
解:2-4 图⽰⼀混合屋架结构的计算简图。
屋架的上弦⽤钢筋混凝⼟制成。
下⾯的拉杆和中间竖向撑杆⽤⾓钢构成,其截⾯均为两个75mm×8mm的等边⾓钢。
已知屋⾯承受集度为的竖直均布荷载。
试求拉杆AE和EG横截⾯上的应⼒。
解:=1)求内⼒取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应⼒75×8等边⾓钢的⾯积A=11.5 cm2(拉)(拉)2-5(2-6)图⽰拉杆承受轴向拉⼒,杆的横截⾯⾯积。
如以表⽰斜截⾯与横截⾯的夹⾓,试求当,30,45,60,90时各斜截⾯上的正应⼒和切应⼒,并⽤图表⽰其⽅向。
解:2-6(2-8) ⼀⽊桩柱受⼒如图所⽰。
柱的横截⾯为边长200mm的正⽅形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的⾃重,试求:(1)作轴⼒图;(2)各段柱横截⾯上的应⼒;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)2-7(2-9)⼀根直径、长的圆截⾯杆,承受轴向拉⼒,其伸长为。
试求杆横截⾯上的应⼒与材料的弹性模量E。
解:2-8(2-11)受轴向拉⼒F作⽤的箱形薄壁杆如图所⽰。
已知该杆材料的弹性常数为E,,试求C与D两点间的距离改变量。
解:横截⾯上的线应变相同因此2-9(2-12) 图⽰结构中,AB为⽔平放置的刚性杆,杆1,2,3材料相同,其弹性模量E=210GPa,已知,,,。
试求C点的⽔平位移和铅垂位移。
解:(1)受⼒图(a),。
(2)变形协调图(b)因,故=(向下)(向下)为保证,点A移⾄,由图中⼏何关系知;第三章扭转3-1 ⼀传动轴作匀速转动,转速,轴上装有五个轮⼦,主动轮Ⅱ输⼊的功率为60kW,从动轮,Ⅰ,Ⅲ,Ⅳ,Ⅴ依次输出18kW,12kW,22kW和8kW。


矩形截面横力弯曲梁横截面切应力最大值在工程力学中,横力弯曲是指梁在受到横向力作用时所发生的弯曲变形。
这时梁的截面上会受到横向剪切力,导致横截面内部产生切应力。
而矩形截面横力弯曲梁的横截面切应力最大值是指在受到横力作用时,矩形截面梁的截面上切应力的最大值。
在分析矩形截面横力弯曲梁横截面切应力最大值时,我们首先要了解梁的受力情况。
一般来说,当梁受到横向力作用时,梁的上部受拉,下部受压,这会引起梁的横截面产生一定的切应力。
而在矩形截面横力弯曲梁中,切应力的最大值通常出现在截面的中性轴上,也就是位于梁的截面中点处。
为了求解矩形截面横力弯曲梁横截面切应力的最大值,我们需要利用弯矩和剪力的关系来进行分析。
在横力弯曲梁中,弯矩和剪力之间的关系可以用以下公式表示:$$\tau = \frac{VQ}{It}$$在这个公式中,τ代表切应力,V代表剪力,Q代表截面的矩形抵抗矩,I代表截面的惯性矩,t代表截面的厚度。
根据这个公式可以看出,在给定梁的截面形状和受力条件下,切应力的最大值取决于剪力的大小和截面的形状。
在实际工程中,为了求解矩形截面横力弯曲梁横截面切应力的最大值,我们可以采用截面分析的方法。
我们可以根据梁的几何形状计算出截面的惯性矩和矩形抵抗矩。
根据外部载荷和支座反力的大小,可以确定梁在不同位置的剪力大小。
将这些数据代入上面的公式中,就可以求解出矩形截面横力弯曲梁横截面切应力的最大值。
矩形截面横力弯曲梁横截面切应力的最大值是在横力作用下,梁截面上切应力的最大值。
通过对梁的受力情况和截面形状进行分析,我们可以求解出切应力的最大值,这对于工程设计和结构分析具有重要的意义。
在实际工程中,我们可以通过截面分析的方法来求解切应力的最大值,以保证结构的安全可靠。
矩形截面横力弯曲梁横截面切应力的最大值是横力作用下梁截面切应力的最大值。
因为横向力作用引起了梁的弯曲变形,导致梁截面内部产生了切应力。
通过分析梁的受力情况和截面形状,可以求解出切应力的最大值。
第二章杆件内力与内力图2-2(b)、(d)、(g)试作图示各杆的轴力图,并确定最大轴力| F N |max 。
2-3(b)试求图示桁架各指定杆件的轴力。
2-4(c)试作图示各杆的扭矩图,并确定最大扭矩| T |max 。
2-5图示一传动轴,转速n =200 r/min ,轮C为主动轮,输入功率P=60 kW ,轮A、B、D均为从动轮,输出功率为20 kW,15 kW,25 kW。
(1)试绘该轴的扭矩图。
(2)若将轮C与轮D对调,试分析对轴的受力是否有利。
2-8(a)、(c)、(e)、(g)、(h)试列出图示各梁的剪力方程和弯矩方程。
作剪力图和弯矩图,并确定|F s |max及|M |max值。
2-9(a)、(c)、(d)、(f)、(g)、(i)、(k)、(l)、(m)试用简易法作图示各梁的剪力图和弯矩图,并确定|F s |max及|M |max值,并用微分关系对图形进行校核。
2-10设梁的剪力图如图(a)(d)所示(见教材p39)。
试作弯矩图和荷载图。
已知梁上无集中力偶。
2-11(b)试用叠加法绘出图示梁的弯矩图。
2-6一钻探机的功率为10 kW,转速n =180 r/min。
钻杆钻入土层的深度l= 40m。
若土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m,并作钻杆的扭矩图。
2-14图示起重机横梁AB承受的最大吊重F P=12kN,试绘出横梁AB的内力图。
第三章轴向拉压杆件的强度与变形计算3-1图示圆截面阶梯杆,承受轴向荷载F1=50kN与F2的作用,AB与BC段的直径分别为d1=20mm与d2=30mm,如欲使AB与BC段横截面上的正应力相同,试求荷载F2之值。
3-5变截面直杆如图所示。
已知A1=8cm2,A2=4cm2,E=200GPa 。
求杆的总伸长量。
3-7图示结构中,AB为水平放置的刚性杆,1、2、3杆材料相同,其弹性模量E=210GPa ,已知l =1m,A1=A2=100mm2,A3=150mm2,F P=20kN 。
圆轴扭转时横截面上的切应力分布规律下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!圆轴扭转时横截面上的切应力分布规律1. 引言圆轴扭转是工程中常见的力学现象,而横截面上的切应力分布规律是研究圆轴扭转的重要内容之一。
1.轴横截面上的最大切应力
轴横截面上的最大切应力是指轴承受的最大切削力在横截面上的最大剪应力。
在机械
设计和工程中,轴横截面上的最大切应力是一项重要的指标,它反映出轴在承载和传递力
矩时的强度和耐久性能,对于轴的设计和选择具有重要意义。
在理论力学中,我们可以通过静力学方法来计算轴横截面上的最大切应力。
在轴承载
工作时,由于外界力的作用,轴受到一定的弯曲和扭转,使得轴截面上的材料遭受拉和压,同时也发生剪切应力,其中剪应力最大值就是轴截面上的最大切应力。
我们可以通过以下公式计算轴横截面上的最大切应力:
τ_max = T_max / J
其中,τ_max为最大切应力,T_max为轴的最大扭矩,J为轴横截面的极振截面系
数。
极振截面系数J是一个与轴形状和尺寸有关的物理量,它描述了轴旋转时各截面的抗
剪切能力,也是计算最大切应力的重要参数。
常用的轴形状包括圆形、方形、三角形等,
通过不同的形状和尺寸来实现对J值的优化。
在轴的设计中,我们通常会考虑加强轴的强度和刚度,以保证承载力和传递能力,在
此基础上尽量减小轴的重量和体积,以提高轴的技术经济性和实用性。
为此,我们需要综
合考虑轴的材料、形状、尺寸、工艺等诸多因素,以满足轴的功能和性能要求。
在实际工程中,轴横截面上的最大切应力是影响轴使用寿命和安全性的重要因素,只
有通过科学的设计和制造,才能保证轴的可靠性和稳定性,为机械工程发挥更大的作用。