第八章弹性杆件横截面上正应力分析
- 格式:ppt
- 大小:1.16 MB
- 文档页数:36


教学设计三杆件弯曲受力分析计算在学习绘制杆件弯曲受力分析图后,我们来学习一下杆件的弯曲受力分析计算,即我们杆件弯曲时在横截面上产生的弯曲正应力和弯曲剪应力的计算。
问题一,杆件弯曲横截面正应力计算问题梁在弯曲变形时,梁轴线方向截面纤维曲线,下部拉伸变长,上部压缩变短。
我们选取杆件的某段横截面,其截面上某处的微分段面积dA如图8.2所示。
由该截面的积分得到,截面为弯矩M大小为公式8.1。
(公式8.1)根据广义胡可定律得到公式8.2与弯曲应变几何条件分析公式8.3得到公式8.4。
(公式8.2)(公式8.3)(公式8.4)其中,ρ为梁弯曲的曲率半径。
将公式8.4和8.1合并得到公式8.5。
(公式8.5)分析公式8.5,其中:为截面绕Z轴的惯性矩。
公式8.5变形为8.6。
ρρρρρεyydxdx==-+=∆=dθdθdθdθy)dθ(⎰⋅=AyM dAσεσ⋅=EρεσyEE==⎰⎰⎰=⎪⎪⎭⎫⎝⎛=⋅=AA AyEyyEyM dAdAdA2ρρσZAIy=⎰dA2(公式8.6)将公式8.6与公式8.4合并,得到公式8.7(公式8.7)公式8.7为杆件弯曲截面上弯曲正应力一般计算公式。
如图8.2所示,y 为惯性轴到所计算应力位置的距离,分析公式我们发现当y 为0时,截面正应力为零,当y 等于截面高度一半时,截面正应力最大,说明在杆件中间有一条纤维线在受力弯曲时既不拉伸变长也不压缩变短,我们称这条纤维曲线为杆件的中性轴,此轴所在的水平层称为中性层,而在杆件截面上下边缘处,存在最大弯曲拉应力和最大弯曲压应力,也就是极值问题的出现。
我们引入新的物理量W ,抗弯截面模量,它的计算式为8.8。
(公式8.8)公式8.7可以化简为极值公式8.9。
(公式8.9)例题分析讲解 【例1】图8.3所示,悬臂矩形截面杆件,截面O 1上有A 、B 、C 、D 点,求它们的弯曲正应力。
【解】计算悬臂梁的弯矩计算梁截面的惯性矩计算抗弯截面模量 计算各点的正应力yIW Z=m kN 6.488.130212⋅=⨯⨯=M 001067.0124.02.01233=⨯==bh I 00533.0124.02.0622=⨯==bh W Z WM Z =σZZ I E M ⋅=ρ1y I M ZZ=σ(拉)MPa 12.900533.06.48===Z Z a W M σ(压)m 9.12kN a d ⋅=-=σσ0b =σ(压)4.55MPa 0.1106700.06.48b c =⨯==y I M Z Z σ问题二,杆件弯曲横截面剪应力计算问题与弯曲正应力不同,在截面上各点的弯曲剪应力指向相同,不论是否在中性层的上侧还是下侧;在同一剪力段,同一层的各点剪应力大小相同。



工程力学中的杆件和梁的应力分析工程力学是工程学科的重要分支之一,它研究物体在受力作用下的力学性质。
在工程实践中,杆件和梁是常见的结构构件,其应力分析是工程设计和计算的基础。
本文将从杆件和梁的应力分析角度探讨工程力学中的相关知识。
一、杆件的应力分析杆件是一种细长的结构构件,承受轴向力的作用。
在杆件的静力学中,应力是一个重要参数,用于描述杆件内部受力的强度和稳定性。
杆件的应力可以分为正应力和切应力。
1. 正应力正应力是指垂直于杆件截面的作用力在该截面上的单位面积,通常用σ表示。
正应力的计算可以使用公式:σ = F / A其中,F为作用力的大小,A为截面积。
正应力可以分为拉应力和压应力两种情况。
当作用力沿着杆件的轴向,方向与截面的法线方向一致时,称为拉应力。
拉应力是正值,表示杆件受拉的状态。
当作用力沿着杆件的轴向,方向与截面的法线方向相反时,称为压应力。
压应力是负值,表示杆件受压的状态。
2. 切应力切应力是指杆件截面上作用力的切向力与该截面上的单位面积之比,通常用τ表示。
切应力的计算可以使用公式:τ = F / A其中,F为作用力的大小,A为截面积。
切应力主要存在于杆件的连接部分,例如螺纹连接、焊接连接等。
切应力会引起杆件的剪切变形和破坏,需要在设计过程中加以考虑。
二、梁的应力分析梁是一种用于承受弯曲力的结构构件,具有横截面的特点。
在梁的应力分析中,主要考虑的是弯矩和截面弯曲应力。
1. 弯矩弯矩是指作用在梁上的力对其产生的弯曲效应。
在工程实践中,梁通常是直线形状,因此弯矩在横截面上呈现出分布的特点。
弯矩可以通过力学平衡和弹性力学原理进行计算。
弯矩的大小与力的大小和作用点的位置有关,计算公式为:M = F * d其中,M为弯矩,F为作用力的大小,d为作用点到梁的某一端的距离。
2. 截面弯曲应力截面弯曲应力是指由于弯曲效应,在梁的横截面上产生的应力。
截面弯曲应力的大小与弯矩和横截面的几何形状有关,计算可以使用弯曲应力公式进行。

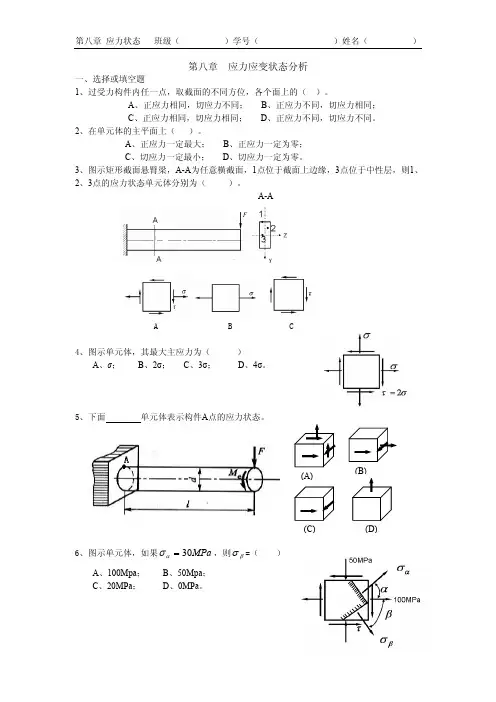
第八章 应力应变状态分析一、选择或填空题1、过受力构件内任一点,取截面的不同方位,各个面上的( )。
A 、正应力相同,切应力不同;B 、正应力不同,切应力相同;C 、正应力相同,切应力相同;D 、正应力不同,切应力不同。
2、在单元体的主平面上( )。
A 、正应力一定最大;B 、正应力一定为零;C 、切应力一定最小;D 、切应力一定为零。
3、图示矩形截面悬臂梁,A-A 为任意横截面,1点位于截面上边缘,3点位于中性层,则1、2、3点的应力状态单元体分别为( )。
A-AA B C4、图示单元体,其最大主应力为( )A 、σ;B 、2σ;C 、3σ;D 、4σ。
5、下面 单元体表示构件A 点的应力状态。
6、图示单元体,如果MPa 30=ασ,则βσ=( ) A 、100Mpa ; B 、50Mpa ; C 、20MPa ; D 、0MPa 。
(C)7、图示单元体应力状态,沿x 方向的线应变εx 可表示为( )A 、Eyσ; B 、)(1y x E μσσ−;C 、)(1x y E μσσ− ;D 、Gτ。
8、图示应力圆对应于单元体( )。
9、已知单元体及应力圆如图所示,σ1所在主平面的法线方向为( )。
A 、n 1;B 、 n 2;C 、n 3;D 、n4。
二、计算题1、已知应力状态如图所示,试用解析法计算图中指定截面上的正应力和切应力。
2、试画图示应力状态的三向应力圆,并求主应力、最大正应力和最大切应力。
3、边长为20mm的钢立方块置于刚性模中,在顶面受力F=14kN作用。
已知材料的泊松比为0.3,求立方体各个面上的正应力。
4、图示矩形截面梁某截面上的弯矩和剪力分别为M=10 kN.m,Q=120 kN。
试绘出截面上1、2、3、4各点的应力状态单元体,并求其主应力。
第九章 强度理论一、选择题或填空题 1、在冬天严寒天气下,水管中的水会受冻而结冰。
根据低温下水管和冰所受力情况可知( )。
A 、冰先破裂而水管完好;B 、水管先破裂而冰完好;C 、冰与水管同时破裂;D 、不一定何者先破裂。
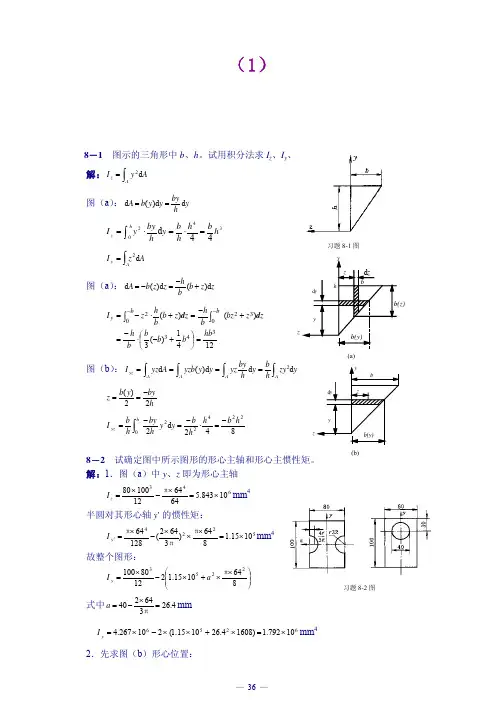



习题7-1图习题7-2图 习题7-3图工程力学(静力学与材料力学)习题第7章 弹性杆件横截面上的正应力分析7-1 桁架结构受力如图示,其上所有杆的横截面均为20mm ×50mm 的矩形。
试求杆CE 和杆DE 横截面上的正应力。
7-2 图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷,其集度p = 10kN/m ,在自由端D 处作用有集中呼F P = 20 kN 。
已知杆的横截面面积A = 2.0×10-4m 2,l = 4m 。
试求:1.A 、B 、E 截面上的正应力;2.杆内横截面上的最大正应力,并指明其作用位置。
7-3 图示铜芯与铝壳组成的复合材料杆,轴向拉伸载荷F P 通过两端的刚性板加在杆上。
试:1.写出杆横截面上的正应力与F P 、d 、D 、E c 、E a 的关系式;2.若已知d = 25mm ,D = 60mm ;铜和铝的单性模量分别为E c = 105GPa 和E a = 70GPa ,F P = 171 kN 。
试求铜芯与铝壳横截面上的正应力。
习题7-4图 习题7-5图 习题7-6图习题7-7图 7-4 图示由铝板钢板组成的复合材料柱,纵向截荷F P 通过刚性平板沿着柱的中心线施加在其上。
试:1.导出复合材料柱横截面上正应力与F P 、b 0、b 1、h 和E a 、E s 之间的关系式;2.已知F P = 385kN ;E a = 70GPa ,E s = 200GPa ;b 0 = 30mm ,b 1 = 20mm ,h = 50mm 。
求铝板与钢板横截面上的最大正应力。
7-5 从圆木中锯成的矩形截面梁,受力及尺寸如图所示。
试求下列两种情形下h 与b 的比值:1.横截面上的最大正应力尽可能小;2.曲率半径尽可能大。
7-6 梁的截面形状为正方形去掉上、下角,如图所示。
梁在两端力偶M z 作用下发生弯曲。
设正方形截面时,梁内最大正应力为0σ;去掉上、下角后,最大正应力变为0max σσk =,试求:1.k 值与h 值之间的关系;2.max σ为尽可能小的h 值,以及这种情形下的k 值。
<<工程力学>>研究生入学考试大纲第一篇刚体静力学1.引论物体的受力分析方法与受力图2.力系的等效与简化力对点的矩;力对轴的矩;主矢与主矩;对力偶及力偶系的应用;力线平移定理;空间一般力系的简化;简化的最后结果;力螺旋;合力矩定理.3.力系的平衡平衡条件;平衡方程;平面力系平衡方程应用于简单多刚体系统;空间力系平衡方程的应用.4.刚体静力学专门问题桁架静力分析的基本方法;滑动摩擦;摩擦角与自锁现象;考虑摩擦的平衡问题;滚动摩擦.第二篇弹性静力学5.引论弹性体及其理想化;弹性体受力与变形特征.6.杆件的内力分析内力主矢主矩及内力分量;纵向载荷引起的内力图;梁的剪力图与弯矩图;刚架的剪力图与弯矩图;复杂载荷作用下杆件的内力图.7.弹性杆件横截面上的正应力分析应力应变及其相互关系;杆件横截面上的正应力分析;正应力公式的应用;中性轴的概念及其位置;截面核心的概念.8.弹性杆件横截面上的切应力分析圆轴扭转时横截面上的切应力;非圆截面杆扭转时的切应力;弯曲中心.9.应力状态分析一点处应力状态描述及其分类;正负号规则;微元的局部平衡,应力坐标变换;应力圆的应用;主应力主方向与面内最大切应力;三向应力状态的特例分析;广义虎克定律;各向同性材料个弹性常数之间的关系;总应变比能;体积改变比能与形状改变比能.10.杆件横截面的位移分析微段的变形;杆件的总体变形与横截面的位移;积分法确定梁的挠度与转角;叠加法求变形及位移;简单的超静定问题.11.弹性平衡稳定性分析弹性稳定性的基本概念;确定分叉载荷的平衡方法12.失效分析与设计准则应力-应变曲线;弹性模量;比例极限;弹性极限;屈服应力;应变硬化与颈缩;拉延行为;强度极限;延伸率;韧性指标;卸载与再加载时材料的力学行为;单向压缩时材料的力学行为;材料在单向应力状态下的失效判据;杆件失效概念与失效分类;屈服准则;断裂准则;稳定性设计准则.13.杆类构件的静力学设计拉压杆的强度设计;梁的强度设计;梁的刚度设计;轴的强度设计;压杆稳定性设计;组合变形杆件的强度设计;提高构件强度的途径;提高构件刚度的途径;提高压杆承载能力的途径.第三篇工程运动学1.点的一般运动点的运动方程速度与加速度;变矢量法;直角坐标法;弧坐标法;切向加速度;法向加速度.2 点的复合运动绝对运动相对运动与牵连运动;矢量的绝对导数与相对导数;速度合成定理;加速度合成定理;科氏加速度;3. 刚体平面运动刚体平面于的自由度广义坐标与运动方程;平面运动分解为平移与转动;平面运动的角速度概念;基点法;速度投影定理法;瞬时速度中心法;平面图形上各点的加速度分析;平面运动分解为转动与转动.第四篇工程动力学4.质点在惯性与非惯性参考系中的动力学质点在惯性系中的运动微分方程;质点动力学第二类问题的应用; 质点在非惯性系中的运动微分方程;牵连惯性力与科氏惯性力的概念.定理5.质点系动量定理动量定理与质量中心运动定理;应用于简单刚体系统;应用于定常质量流;变质量质点的运动微分方程.6.质点系动量矩定理质点系动量矩定理及应用; 质点系相对于质心动量矩定理;刚体平面运动微分方程及应用7.质点系动能定理动量与能量;内力之功与理想约束力之功;质点系的动能与刚体的动能;质点系的动能定理与机械能守恒;质点系普遍定理的综合应用.8. 达朗贝尔原理达朗贝尔原理与惯性力; 达朗贝尔原理的质点系形式;刚体惯性力系的简化;动静法的应用.9.碰撞碰撞的力学特征与模型;动力学普遍定理在碰撞问题中的应用;恢复系数;两球的斜碰撞;刚体的碰撞;撞击中心.10.振动单自由度线性系统的自由振动; 单自由度线性系统的受迫振动;第五篇分析力学1.引论约束;广义坐标与自由度;虚位移与虚功;理想约束.2.虚位移原理虚位移原理及其应用;保守系统和势能的基本概念;势能驻值定理;最小势能原理.3.分析动力学基础分析动力学的基本概念达朗贝尔-拉格朗日原理及应用;拉格朗日方程的推导,形式及应用;拉格朗日方程的首次积分.参考教材:《工程力学教程》(I、II、III第一版),高等教育出版社,范钦珊。