高斯—牛顿迭代法

高斯—牛顿迭代法高斯-牛顿迭代法是一种重要的数值解方法，它为解决复杂的非线性方程提供了一种有效的途径。

它结合了高斯原理和牛顿法的优势，利用高斯消元方法解出方程的一个精确解，从而有效地解决复杂的非线性方程组。

首先，我们来看看高斯-牛顿迭代法的基本思想。

很显然，这种迭代法是基于高斯原理以及牛顿法的思想。

根据高斯原理，可以得到每一个未知数的一个精确解。

而牛顿法则通过更新未知数的近似值，使得这个近似解更接近真实的解。

在这种思路的指导下，我们引入了高斯-牛顿迭代法，它具有非常高的效率和准确率。

其次，我们来看看高斯-牛顿迭代法的步骤以及具体实现过程。

高斯-牛顿迭代法的步骤主要有四步：首先，通过高斯消元算法求解出精确解；接着，通过求解线性方程组的近似解来更新未知数的初值；第三步，对更新的初值求解线性方程组，同时也计算出该近似解的梯度；最后，运用牛顿法更新未知数的近似值，并重复上述的求解步骤，直到收敛。

另外，在实际使用高斯-牛顿迭代法时，我们还需要考虑一些实际问题，例如对于牛顿迭代中未知数的初值选取，以及求解过程中收敛度控制等等。

不同的初值会影响最终求解过程的收敛速度和收敛精度，而牛顿法的收敛率又受到梯度的影响，因此，在实际应用中，需要考虑如何选择初值以及如何控制收敛度，这些问题都是高斯-牛顿迭代法内容中非常重要的一部分。

最后，我们来看看高斯-牛顿迭代法在实际应用中的一些典型案例。

在压力容器复合结构分析中，需要求解压力容器复合结构的有限元方程组，这其中含有大量非线性方程，而高斯牛顿迭代法可以有效地求解这样的问题；此外，高斯-牛顿迭代法也可以应用于组合优化的求解中，这类优化问题包括多目标优化、非线性约束优化等；另外，高斯牛顿迭代也可以用于求解动力系统中牛顿欧拉方程，如轨道飞行器动力学模型中的牛顿欧拉方程等。

总之，高斯-牛顿迭代法是一种有效的数值解方法，它结合了高斯原理和牛顿法的优势，可以有效地解决复杂的非线性方程组，而且具有收敛性好、效率高、准确率高的特点。

高斯牛顿法高斯—牛顿迭代法的基本思想是使用泰勒级数展开式去近似地代替非线性回归模型，然后通过多次迭代，多次修正回归系数，使回归系数不断逼近非线性回归模型的最佳回归系数，最后使原模型的残差平方和达到最小。

高斯—牛顿法的一般步骤为：(1)初始值的选择。

其方法有三种，一是根据以往的经验选定初始值；二是用分段法求出初始值；三是对于可线性化的非线性回归模型，通过线性变换，然后施行最小平方法求出初始值。

(2)泰勒级数展开式。

设非线性回归模型为：i=1,2,…,n (3-68)其中r为待估回归系数，误差项～N(0, )，设：，为待估回归系数的初始值，将(3-68)式在g点附近作泰勒展开，并略去非线性回归模型的二阶及二阶以上的偏导数项，得(3-69)将(3-69)式代入(3-68)式，则移项：令：则：i=1,2，…，n用矩阵形式表示，上式则为：(3-70)其中：(3)估计修正因子。

用最小平方法对(3-70)式估计修正因子B，则：(3-71)设g为第一次迭代值，则：(4)精确度的检验。

设残差平方和为：，S为重复迭代次数，对于给定的允许误差率K，当时，则停止迭代；否则，对(3-71)式作下一次迭代。

(5)重复迭代。

重复(3-71)式，当重复迭代S次时，则有：修正因子：第(S+1)次迭代值：四、应用举例设12个同类企业的月产量与单位成本的资料如下表：表3-9 间接代换法计算表企业编号单位产品成本（元）月产量1 2 3 4 5 6 7 8 91011121601511141288591757666606160101620253136404551566065(注：资料来源《社会经济统计学原理教科书》第435页)试配合适当的回归模型分析月产量与单位产品成本之间的关系。

解：(1)回归模型与初始值的选择。

根据资料散点图的识别，本数据应配合指数模型：对指数模型两边取对数，化指数模型为线性回归模型，然后施行最小平方法求出初始值。

即：则上述指数模型变为：对分别求反对数，得，带入原模型，得回归模型：高斯—牛顿迭代法初始回归模型：残差平方和：（2）泰勒级数展开式。

实验二：迭代法求解方程组姓名：徐烨学号：08072105时间：2010-11-17一、实验目的利用jacobi 迭代法和gauss-seidei 迭代法求解线性方程组，利用newton 迭代法求解非线性方程组。

在求解过程中，利用这三种方法的迭代原理，根据迭代法的求解流程，写出三种迭代法的迭代格式，学习三种迭代法的原理和解题步骤，并使用matlab 软件求解方程。

在实验过程中，分别取不同的初值进行求解，并做结果分析，解怒同德方程来比较这三种迭代方法的利弊。

二、实验步骤newton 迭代法⒈newton 迭代原理考虑非线性方程f(x)=0，求解她的困难在于f 是非线性函数。

为克服这一困难，考虑它的线性展开。

设当前点为Xk, 在Xk 处的Taylor 展开式为f ()x ≈f ()()()k k k x x x f x -'+令上式右端为0.解其方程得到()()k k k k x f x f x x '-=+1 ⋅⋅⋅=1,0k 此式就称为Newton 公式。

2. newton 迭代法的matlab 实现function x=newton(fname,dfname,x0,e,N)%用途：牛顿迭代法解非线性方程组分f(x)=0%fname 和dfname 分别表示f(x)及其到函数的M 函数句柄或内嵌函数的表达式%x0为迭代初值，e 为精度%x 为返回数值解，并显示计算过程，设置迭代次数上线N 以防发散if nargin<5,N=500;endif nargin<4,e=le-4;endx=x0;x0=x+2*e;k=0;fprintf('It.no=%2d x%[2d]=%12.9f\n',k,k,x)while abs(x0-x)>e&k<Nk=k+1;x0=x;x=x0-feval(fname,x0)/feval(dfname,x0);fprintf('It.no=%2d x[%2d]=%12.9f\n',k,k,x) endif k==N,fprintf('已达到迭代次数上限');end在试验中，我用这种方法求f(x)=x3-3*x-1=0的解①初值为2时，新建一个文件，输入：fun=inline('x^3-3*x-1');dfun=inline('3*x^2-3');x=newton(fun,dfun,2,0.5e-6)即可得此方程的解为：It.no= 0 xIt.no= 1 x[ 1]= 1.888888889It.no= 2 x[ 2]= 1.879451567It.no= 3 x[ 3]= 1.879385245It.no= 4 x[ 4]= 1.879385242x =1.879385241571817e+000②初值为5时，新建一个文件，输入：fun=inline('x^3-3*x-1');dfun=inline('3*x^2-3');x=newton(fun,dfun,5,0.5e-6)即可得此方程的解为：It.no= 0 xIt.no= 1 x[ 1]= 3.486111111It.no= 2 x[ 2]= 2.562343095It.no= 3 x[ 3]= 2.075046554It.no= 4 x[ 4]= 1.902660228It.no= 5 x[ 5]= 1.879777024It.no= 6 x[ 6]= 1.879385355It.no= 7 x[ 7]= 1.879385242x =1.879385241571826e+000③初值为8时，新建一个文件，输入：fun=inline('x^3-3*x-1');dfun=inline('3*x^2-3');x=newton(fun,dfun,8,0.5e-6)即可得此方程的解为：It.no= 0 xIt.no= 1 x[ 1]= 5.423280423It.no= 2 x[ 2]= 3.754505841It.no= 3 x[ 3]= 2.719579123It.no= 4 x[ 4]= 2.148629510It.no= 5 x[ 5]= 1.920654127It.no= 6 x[ 6]= 1.880593045It.no= 7 x[ 7]= 1.879386323It.no= 8 x[ 8]= 1.879385242It.no= 9 x[ 9]= 1.879385242x =1.879385241571817e+000gauss-seidel 实验过程1.gauss-seidel 迭代原理将方程组Ax=b （设n i a n ,2,1;0⋅⋅⋅=≠）化成等价方程组：)(1∑≠-=ij j i i i i x a b a x j i ),2,1(n i ⋅⋅⋅= 采用迭代格式： ⎪⎪⎭⎫ ⎝⎛--=∑∑-=+=++111111i j n i j k jij k j ij i ij k i x a x a b a x ()n i ⋅⋅⋅⋅=,2,1 2.gauss-seidel 迭代法的matlab 实现function x=jacobi(A,b,x0,emg,N)% A 是线性方程组的系数矩阵% b 是值向量% x0是迭代初始向量% N 是迭代上限，诺迭代次数大于>N,则迭代失败% emg 是控制精度% 用gauss-seidei 迭代法求解线性方程组Ax=b 的解%k 表示迭代次数%x 表示用迭代法求得的解线性方程组的近似解if nargin<5N=500;else N=N;endn=length(b);x1=zeros(n,1);x2=zeros(n,1);x1=x0;k=0;r=max(abs(b-A*x1));while r>emgfor i=1:nsum=0;for j=1:nif i~=jsum=sum+A(i,j)*x1(j);endendx2(i)=(b(i)-sum)/A(i,i);endr=max(abs(x2-x1));x1=x2;k=k+1;if k>Nwarning('迭代次数达到上限！');return;endendx=x1；在试验中，我用此方法求①A1=922282217 ，b=6810的线性方程组的解 新建一个文件，输入：A=[7 1 2;2 8 2;2 2 9];b=[10 8 6]';x0=[0 0 0]';emg=10^(-6);x=gaussseidel(A,b,x0,emg)可得此方程的解为：x =1.269406363593758e+0006.210045136516440e-0012.465753606121330e-001改变此初值为x0=[1 2 3]’时，可得此方程的解为：x =1.269406358870516e+0006.210045989420114e-0012.465753427083272e-001②A2=32-1-1-102-2-2-10 ，b=15.01的线性方程组的解 新建一个文件，输入：A=[10 -2 -2;-2 10 -1;-1 -2 3];b=[10 8 6]';x0=[0 0 0]';emg=10^(-6);x=gaussseidel(A,b,x0,emg)即可得此方程的解为：x =2.067226785332675e+0001.588235242744889e+0003.747899090274151e+000改变此初值为x0=[4 5 6]’时，可得此方程的解为：x =2.067226982320636e+0001.588235338736795e+0003.747899219931409e+000jacobi 迭代法的实验过程1.jacobi 迭代原理将方程组Ax=b （设n i a n ,2,1;0⋅⋅⋅=≠）化成等价方程组：)(1∑≠-=ij j i i i i x a b a x j i ),2,1(n i ⋅⋅⋅= 采用迭代格式:⎪⎪⎭⎫ ⎝⎛-=∑≠+111j k j ij i ii k i x a b a x ()n i ⋅⋅⋅=,2,1 2.Jacobi 迭代法的matlab 实现function x=jacobi(A,b,x0,emg,N)% A 是线性方程组的系数矩阵% b 是值向量% x0是迭代初始向量% N 是迭代上限，诺迭代次数大于>N,则迭代失败% emg 是控制精度% 用jacobi 迭代法求解线性方程组Ax=b 的解%k 表示迭代次数%x 表示用迭代法求得的解线性方程组的近似解if nargin<5N=500;else N=N;endn=length(b);x1=zeros(n,1);x2=zeros(n,1);x1=x0;k=0;r=max(abs(b-A*x1));while r>emgfor i=1:nsum=0;for j=1:nif i~=jsum=sum+A(i,j)*x1(j);endendx2(i)=(b(i)-sum)/A(i,i);endr=max(abs(x2-x1));x1=x2;k=k+1;if k>Nwarning('迭代次数达到上限！');return;endendx=x1；在实验中，我用此方法求①A1=922282217 ，b=6810的线性方程组的解，这样可以比 这两种方法的优越性新建一个文件，输入：A=[7 1 2;2 8 2;2 2 9];b=[10 8 6]';x0=[0 0 0]';emg=10^(-6);x=jacobi(A,b,x0,emg)即可得此方程的解为：x=1.269406606540146e+0006.210048051684348e-0012.465755635845312e-001改变此初值为x0=[1 2 3]’时，可得此方程的解为：x =1.269406576962693e+0006.210047721178078e-0012.465755330013612e-001②A2=32-1-1-102-2-2-10 ，b=15.01的线性方程组的解 新建一个文件，输入：A=[10 -2 -2;-2 10 -1;-1 -2 3];b=[10 8 6]';x0=[0 0 0]';emg=10^(-6);x=jacobi (A,b,x0,emg)即可得此方程的解为：x =2.067226548410933e+0001.588235036073759e+0003.747898577034409e+000改变此初值为x0=[4 5 6]’时，可得此方程的解为：x =2.067227297951090e+0001.588235601041707e+0003.747899852657807e+000三、实验分析由Jacobi 的迭代公式可以看到，在计算机上使用该法线性方程组时，x(m)分量必须保存到x(m+1)的分量全部复出后才不再需要。

牛顿迭代法的函数逼近和拟合在数学和计算机科学中，函数逼近（function approximation）和拟合（function fitting）是重要的问题之一，它们涉及到如何用已知数据或函数来找出与之近似的函数形式。

而牛顿迭代法是一种常用的数值计算方法，可以被广泛地应用在函数逼近和拟合中。

一、牛顿迭代法简介牛顿迭代法是一种求解方程的方法，其本质是一种迭代算法，可以通过给出一个函数在某点的值以及该点的导数，迭代地求出函数的零点或者极值点。

其基本公式为：$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$其中，$f(x_n)$表示函数在点$x_n$处的函数值，$f'(x_n)$表示函数在点$x_n$处的导数，$x_{n+1}$是通过迭代算法得到的新的近似解。

在使用牛顿迭代法时，需要注意函数的光滑性和局部收敛性，如果函数不光滑或者在某些点处导数为零，那么迭代可能会导致发散或者收敛速度极慢。

二、牛顿迭代法在函数逼近中的应用在函数逼近中，如果我们已知一些数据点$(x_i, y_i)$，并且想要找到一个函数$f(x)$，可以用这些数据点来拟合函数，那么可以使用牛顿迭代法来实现。

具体的方法如下：1.首先定义一个函数$g(x)$，它满足$g(x_i)=y_i$；2.然后利用牛顿迭代公式，给出$f(x)$的递归式：$$f(x_{n+1})=f(x_n)+\frac{g(x_n)-f(x_n)}{g'(x_n)}$$其中，$g(x)$是一个在点$(x_i, y_i)$处值为$y_i$，在其他点处为零的光滑函数。

3.重复进行上述迭代，直到得到一个满足精度要求的近似解。

通过牛顿迭代法的函数逼近方法，我们可以得到在数据点上的逼近函数，这个函数可以用来进行插值和外推等操作，同时也可以作为一个简单的近似模型来使用。

三、牛顿迭代法在函数拟合中的应用除了函数逼近，牛顿迭代法还可以用于函数拟合，这里的函数拟合指的是通过一些给定的函数基，将一个在某些点处已知函数值的函数表示为基函数线性组合的形式。

python高斯-牛顿迭代法-回复题目：Python高斯牛顿迭代法解析- 优化非线性问题摘要：高斯牛顿迭代法是一种用于求解非线性方程组的优化算法。

本文将介绍高斯牛顿迭代法的原理和使用Python实现的步骤。

我们将以一个简单的实例来说明算法的应用，并解释其背后的数学原理。

最后，我们将讨论高斯牛顿迭代法的优势和局限性。

引言：高斯牛顿迭代法是一种被广泛使用的数值优化算法，用于解决非线性问题。

不同于求解线性方程组的高斯消元法，高斯牛顿迭代法专门用于求解非线性问题。

它的应用领域涵盖了各个科学和工程领域，如计量经济学、计算机视觉和机器学习。

本文将详细介绍高斯牛顿迭代法的原理和实现步骤。

我们将以一个简单的实例来演示算法的工作原理，并对其数学背后的原理进行解析。

一、高斯牛顿迭代法原理高斯牛顿迭代法的目标是通过迭代的方式逼近方程组的根。

为了便于理解，我们以一个简单的二次曲线拟合问题为例。

假设我们有一组观测数据点(xi，yi)，我们希望通过一个二次曲线y = a * x^2 + b * x + c来拟合这些数据。

我们的目标是找到最佳的参数a、b 和c，使得拟合曲线与观测数据点的差异最小。

为了达到这个目标，我们可以定义一个误差函数E(a，b，c)来衡量拟合曲线和观测数据点之间的差异。

常见的误差函数有平方和误差函数，即E(a，b，c) = Σ(yi - (a * xi^2 + b * xi + c))^2。

我们的目标是最小化误差函数，即找到使得E(a，b，c)最小的a、b和c。

高斯牛顿迭代法通过迭代的方式逼近最佳参数。

二、高斯牛顿迭代法步骤1. 初始化参数：初始化a、b和c的初始值。

2. 计算雅可比矩阵：雅可比矩阵是误差函数对参数的偏导数矩阵。

对于二次曲线拟合问题，雅可比矩阵J可以表示为：J = [∂E/∂a, ∂E/∂b, ∂E/∂c]3. 计算梯度向量：梯度向量是误差函数在当前参数值处的梯度，即导数。

梯度向量g可以表示为：g = [∂E/∂a, ∂E/∂b, ∂E/∂c]4. 计算海森矩阵：海森矩阵是误差函数对参数的二阶偏导数矩阵。

牛顿迭代法、二分法，定点法的区别与联系牛顿迭代法牛顿迭代法，它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要Newton法是求解方程f(x)=0的最著名的和最有效的数值方法之一，其基本思想可以是将方程转化为线性方程来求解,设f(x)连续可微,则将函数f(x)在x k点处进行taylor展开,即如果,取taylor展开式的线性部分近似代替f(x),得到f(x)=0的近似方程，将此方程的根记作x k+1，则得到这就是Newton迭代公式迭代函数为不动点迭代将方程f(x)=0改写成等价方程则方程的根又称为函数的不动点.为了求的不动点,取一个初始近似值x0,用迭代格式,k=1,2产生序列{x k},这种迭代法我们称之为不动点迭代,或简单迭代又称为迭代函数.假设一个迭代法产生的序列{x k},k=0,1,2,,收敛,，X*是方程f(x)=0的一个解.区间对分法区间对分法是求解方程f(x)=0的一种直观而又简单的迭代法,它是建立在介值定理的理论基础之上的，第一个取值点取在含优区间的1/2处,然后逐渐逼近最优值的单因素试验设计方法。

联系都是用来近似求方程根的方法，利用数列收敛于方程的根。

在应用方面，区间对分法可用来求根的初始近似值,以供其它对初始值要求严格的迭代法使用，牛顿法和不定点迭代法都有局限性，收敛有方向性，如果初始值选的不恰当，则方程不收敛，也就不能得到方程的根。

另外，方程f(x)=0和x=是等价的，于是Newton迭代公式也属于不动点迭代。

区别对分法每次50%的区间舍弃，试验选值跨跃的幅度过大，会使对分法漏掉了最佳值。

从此误差估计式看出,近似解的误差下降速度较慢.但此方法比较简单,且安全可靠.在实际应用中,.需要注意的是此方法只能求单实根,而不能求复根或偶数重根.在牛顿迭代和不动点迭代中，对不动点方程x=，它导出的迭代过程有可能发散，也可能收敛得非常缓慢，注意到x=x和x=都是不动点方程，它们的加权平均h(x)=也是不动点方程，而h(x) 和有完全相同的不动点。

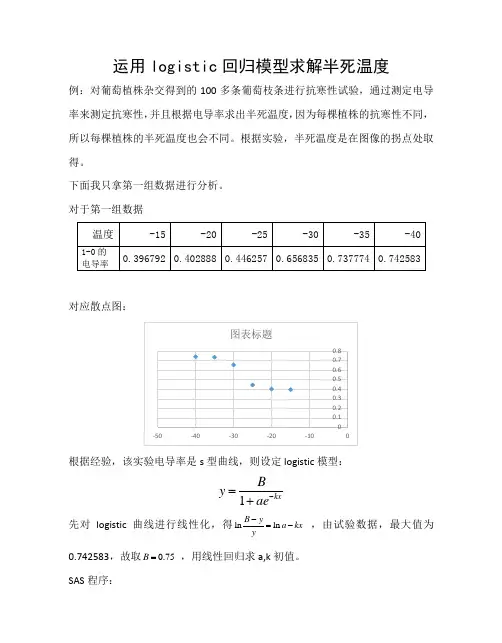
运用logistic 回归模型求解半死温度例：对葡萄植株杂交得到的100多条葡萄枝条进行抗寒性试验，通过测定电导率来测定抗寒性，并且根据电导率求出半死温度，因为每棵植株的抗寒性不同，所以每棵植株的半死温度也会不同。

根据实验，半死温度是在图像的拐点处取得。

下面我只拿第一组数据进行分析。

对于第一组数据对应散点图：根据经验，该实验电导率是s 型曲线，则设定logistic 模型：1kx B y ae -=+先对logistic 曲线进行线性化，得lnln B ya kx y-=- ，由试验数据，最大值为0.742583，故取0.75B = ，用线性回归求a,k 初值。

SAS 程序：data log;input x y;z = log((0.75-y)/y);cards;-15 0.396792302-20 0.402887701-25 0.446256983-30 0.656834532-35 0.73777403-40 0.742582897;proc reg data = log;model z = x;run;SAS结果：由以上结果可得，线性模型为0.75ln3.752020.20498yx y-=+ 即ln 3.75202,0.20498a k =-=，故 3.75202.=,0.20498a e k ==-426070614，以,,B a k 的值作为拟合初值，应用非线性参数估计之高斯—牛顿迭代法。

SAS 程序： data gnewton; set log; keep x y;proc nlin method = gauss;parms b = 0.75 a =42.6070614 k = -0.20498; temp = 1+a*exp(-k*x); model y = b/temp; der.b = 1/temp;der.a = -b*exp(-k*x)/(temp**2); der.k = b*a*exp(-k*x)*x/(temp**2); run ;模型检验，模型显著有效得出参数，如下表由上表可知， 1.1429, 5.6826,0.0621B a k ===- ，所以可得logistic 模型0.06211.14291 5.6826xy e=+对模型求一阶导函数2'(1)kx kx Bae k y ae --=+对模型求二阶导函数22322()''(1)(1)kx kx kx kx B ae k Bae k y ae ae ----=-++把求枝条抗寒的半死温度转化为求原logistic 曲线的拐点，即令''=0y 化简得1ln x a k=把高斯牛顿迭代法得到的a,k 代入上式可得半死温度为27.9776x -=℃。

牛顿迭代法讲解牛顿迭代法是一种优秀的高精度计算方法，其能够快速地求解函数零点和方程的根。

该方法利用了函数在某一点处的导数信息，通过迭代的方式不断逼近真实解，具有快速收敛、高效稳定等优点。

下面将详细地介绍牛顿迭代法的原理和步骤。

一、牛顿迭代法的原理牛顿迭代法的基本思想是：一条曲线在某一点的切线斜率可以近似代替该点处的函数斜率，通过连续斜线的交点，不断逼近真实解。

由此可知，牛顿迭代法的基本原理是利用局部的导数信息来近似全局的函数性质，从而加速问题的求解。

与其他迭代方法相比，牛顿迭代法具有收敛速度快、精度高等优点。

对于平滑的函数而言，它的收敛速度甚至可以达到二次速度，这使得它成为许多求解方程的首选算法。

二、牛顿迭代法的步骤下面我们将介绍牛顿迭代法的具体步骤。

1.确定迭代公式设函数f(x)在x0点可导，则其在x0点的导数可以用以下公式表示：f'(x0) = lim(x->x0) [f(x)-f(x0)]/(x-x0)当x逐渐逼近x0时，上式右边的分数会逼近导数。

因此，我们可以用该式确定迭代公式：xk+1 = xk - f(xk) / f'(xk)其中，x0是初始估计值，xk+1为新的迭代值，xk为上一次的迭代值，f(xk)是函数在xk处的函数值，f'(xk)是函数在xk处的导数值。

2.计算迭代值通过迭代公式，我们可以计算新的迭代值xk+1。

由于初始估计值x0不一定能够很好地逼近真实解，因此我们需要多次迭代，直到迭代值足够接近真实解。

3.判断是否收敛在计算新的迭代值后，我们需要检查其与上一个迭代值之间的差距是否足够小，如果达到了我们预设的收敛精度，则停止计算。

否则，我们需要继续迭代，直到收敛。

4.使用牛顿迭代法求函数零点和方程的根通过上述过程，我们可以利用牛顿迭代法求解函数的零点和方程的根。

具体操作方法如下：（1）将目标函数转化成零点函数，即f(x) = 0（2）选择一个初始估计值x0（3）利用迭代公式计算新的迭代值xk+1 = xk - f(xk) / f'(xk)（4）判断是否达到了收敛精度，如果是，则输出最终结果；如果否，则继续迭代。

牛顿迭代法介绍嘿呀，小伙伴们，今天咱们来唠唠牛顿迭代法这个超有趣的东西。

牛顿迭代法就像是一个超级聪明的小助手，能帮咱们解决好多数学上的难题呢。

它的基本思路啊，就像是在一个迷宫里找宝藏，不过这个迷宫是由函数构成的。

想象一下，你有一个很复杂的函数，就像是一团乱麻，你想找到这个函数等于零的点，也就是这个乱麻的某个特殊位置。

牛顿迭代法就开始它的神奇之旅啦。

它先随便找一个起始点，就好比是你在迷宫入口随便选了一条路。

然后呢，它会根据这个点的一些信息，比如说这个点的函数值和导数值，来计算下一个更接近宝藏（也就是函数零点）的点。

这就像是你在迷宫里根据墙上的一些小提示来决定下一步往哪走。

1. 原理方面这个牛顿迭代法的原理其实是基于切线的思想。

你看啊，一个函数在某一点的切线就像是这个函数在这个点附近的一个近似的直线。

如果这个函数是一条弯弯曲曲的小路，那切线就是在这个点附近铺的一块比较直的木板。

牛顿迭代法就是利用这个切线和x轴的交点来找到下一个更接近函数零点的点。

比如说，我们有一个函数f(x)，它在点x0的切线方程是y - f(x0) = f'(x0)(x - x0)，当y = 0的时候，我们就可以解出x1 = x0 - f(x0)/f'(x0)，这个x1就是下一个更接近函数零点的点啦。

是不是很神奇呢？就像魔法一样，从一个不太准确的点一下子就跳到了一个更接近正确答案的点。

2. 实际应用在实际生活中，牛顿迭代法的应用可广泛啦。

比如说在工程计算里，如果要计算一些复杂结构的平衡点，就可以用牛顿迭代法。

就像盖大楼的时候，要找到大楼结构在各种力作用下平衡的那个点，这个时候牛顿迭代法就像一个得力的小工匠，帮工程师们快速找到答案。

再比如说在计算机图形学里，要处理一些复杂的曲线和曲面，牛顿迭代法也能派上大用场。

它可以帮助计算机快速准确地计算出曲线和曲面的交点等重要信息，就像给计算机的眼睛戴上了一副超清晰的眼镜。

3. 优点和局限性牛顿迭代法有好多优点呢。

暴雨强度公式参数率定方法朱颖元根据实测雨强记录，用最小二乘法为准则的高斯—牛顿迭代法直接求解暴雨公式的参数，算法简单，可以减少计算误差，提高参数的精度。

1 问题的提出短历时暴雨强度公式是城市排水设计中推求雨水量的公式，常用的型式为：(1)式中n——暴雨衰减指数b——时间参数A——雨力，随重现期T而变A与T的关系常采用下式表示：A=A1(1+Clg T)(2)式中A1、C——参数由式(1)、(2)可得：(3)式(3)可表示为：i=f(t,T;A1,B,b,n) (4) 式中f——已知的非线性函数t——暴雨历时T——重现期(自变量)A1、B、b、n——参数暴雨公式中参数的率定目前仍存在一些尚待研究的问题，首先是短历时暴雨资料采用哪种概率理论分布模型［1、2］；其次是统计参数估计。

目前统计参数估计的方法很多，大致可以分两类，第一类为参数估计法；第二类为适线法。

二者均不具有任何约束条件，一次仅能对一个样本进行估参。

短历时暴雨具有多种历时，因此具有多个样本。

若采用上述任一种方法对各种历时的暴雨资料逐一估计出统计参数，再将频率曲线绘在同一张图上，就有可能出现不同历时暴雨频率曲线相交的不合理情况。

除了经验适线法可以人为对参数进行调整外，其余估参方法均无能为力。

而可以同时对多个样本进行参数估计且能协调不同历时暴雨频率曲线之间参数关系的估参方法目前尚未见到。

最后是式(1)中参数率定问题，一般的方法是：先对暴雨资料进行频率分析，求出各种历时指定重现期的设计雨强值。

再对式(1)进行线性化变换，即式(1)两端取对数使之成为一线性方程。

根据设计雨强值用图解法或最小二乘法确定出参数A、b和n。

最后，根据式(2)及算出的A值用最小二乘法推求出参数A1和C。

这种计算方法实际上是多次辗转相关，而辗转相关已被证明是不可能提高计算精度的［3］。

暴雨公式的精度取决于暴雨资料的可靠性和公式中参数的合理性。

笔者认为，在暴雨资料已定的情况下，参数的合理性取决于暴雨公式对实测原始数据的拟合程度，而非对从频率曲线上摘取的数据的拟合程度。

实验三非线性方程的牛顿法和线性方程组的迭代数值求解信息与计算科学金融崔振威201002034031一、实验目的：设计牛顿迭代算法和线性方程组的常用迭代算法二、实验内容：p69.3、p129.1三、实验要求：1、根据题目要求构造迭代格式2、对线性方程组的迭代求解要求构造三种迭代格式3、试比较牛顿迭代法和不动点迭代法的优劣（p69.3）4、试比较线性方程组三种迭代的优劣（收敛和收敛速度）主程序：a、牛顿迭代法程序：function [x,k]=newton(f,p0,e)%求f(x)=0在给定p0的根。

%f为所求的函数f(x)，p0为迭代初始值，e为迭代精度。

k为迭代次数%diff(f)为对函数求导，subs是赋值函数，用数值替代符号变量替换函数例xa=p0;xb=xa-subs(f,xa)/subs(diff(f),xa);k=1;while abs(xa-xb)>e,k=k+1;xa=xb;xb=xa-subs(f,xa)/subs(diff(f),xa);endx=xb;b、雅克比迭代法程序function [x,n]=Jacobi_Solve(A,b,x0,eps,varargin)%求解线性方程组的迭代法%A为方程组的细数矩阵%b方程组的右端项数字的向量组%eps为精度要求，默认值为1e-5%varargin为最大迭代次数，值为100%x为方程组的解%n为迭代次数if nargin==3eps=1.0e-6;M =200;elseif nargin<3returnelseif nargin==5M =varargin{1};endD=diag(diag(A));%求A的对角矩阵L=-tril(A,-1);%求A的下三角矩阵U=-triu(A,1);%求A的上三角矩阵B=D\(L+U);f=D\b;x=B*x0+f;n=1;%迭代次数while norm(x-x0)>=epsx0=x;x=B*x0+f;n=n+1;if(n>=M)disp('迭代次数太多，可能不收敛。

高斯—牛顿迭代法高斯-牛顿迭代法是一种算法，可以有效地求解多元函数的最大值、最小值及极小值，是近期公认的一种高效的求解一元函数和多元函数极值问题的重要方法。

一、历史沿革高斯-牛顿迭代法发源于17th世纪，贝叶斯（1668年-1732年）提出，他曾研究高斯、牛顿和拉格朗日的算法，并综合整理它们的优点，最终形成了高斯-牛顿迭代法。

贝叶斯的研究为下一代数学家们提供了有用的洞见，例如拉格朗日（1646年-1716年）。

他发现了拉格朗日比较法，一种有效求解定积分的方法，并最终将其与贝叶斯的努力结合在一起，形成了高斯-牛顿迭代法。

二、原理及计算方式高斯-牛顿迭代法的基本原理是通过求解一元和多元函数的导数来求极大值、极小值、或极小值。

所以，本算法的步骤主要有以下三步：1.函数的倒数2. 使用迭代法求解函数的极大值、极小值3.据函数的极大值、极小值，推导原函数而计算过程也相当简单，用一个函数表示如下：迭代公式：X[n+1] = X[n] - f（X[n]）/ f’（X[n]）其中，X[n]为初始的不定极小值，f（X[n]）是函数f的结果，f’（X[n]）表示函数f的导函数的结果。

三、应用场景高斯-牛顿迭代法由于其精确、快速，应用非常广泛，可以用来求解函数、线性代数、拟合数据等领域中的数学问题，例如：1.于图像优化中对参数的优化；2.于拟合数据，比如经验散点回归；3.于求解机器学习中的最优解，包括求解最小二乘法、支持向量机、神经网络等；4.于求解调和级数的极限；5.于解决经济、物理、化学、生物学等领域的最优解；6.于求解线性代数中的矩阵最小二乘问题；7.于最优化控制、优化调度、智能计算等场景中的函数优化问题。

四、优点高斯-牛顿迭代法在求极值时具有许多优势：1.算快速、效率高：运用高斯-牛顿迭代法求解极值时，由于采用了迭代法，运算速度快，比其他算法更为高效。

2.算结果精确：由于使用的是高斯-牛顿迭代法，可以接近极限，从而使计算结果更加精确。

牛顿迭代法的原理与应用牛顿迭代法（Newton's method）是一种数值计算方法，主要用于求解非线性方程和优化问题，其基本思想是通过线性逼近来不断逼近函数的零点。

牛顿迭代法是数学上的一个重要概念，应用广泛，并且在实际问题中也有很多应用。

本文旨在介绍牛顿迭代法的原理和应用。

一、牛顿迭代法的原理牛顿迭代法主要用于求解非线性方程的根，其基本思想是通过对函数进行逐次线性逼近来逼近函数的零点。

设 f(x) 在 x_0 处可导，那么函数在 x_0 处的一次泰勒展开式为：f(x)=f(x_0 )+f'(x_0 )(x-x_0 )将 f(x) 置于零，解出 x 的值，则可得到下一个逼近点：x_{1}=x_{0}-\frac{f(x_0)}{f'(x_0)}依照上述的迭代方式不断进行逼近，直到最终的误差小于某个可接受的范围为止。

例如，在求解方程 x^2-2=0 的根时，选择初始值 x_0=1。

然后根据上述迭代方式不断逼近，可以得到以下的结果：x_1=x_0-\frac{f(x_0)}{f'(x_0)}=1-\frac{1}{2}=0.5x_2=x_1-\frac{f(x_1)}{f'(x_1)}=0.5-\frac{-0.5}{1}=1.0x_3=x_2-\frac{f(x_2)}{f'(x_2)}=1.0-\frac{0}{2}=1.0可以看到，通过牛顿迭代法可以在三次迭代内得到非常精确的解。

同时，牛顿迭代法还可以求解多元函数的根和优化问题，但是在这里不进行详细介绍。

二、牛顿迭代法的应用牛顿迭代法在实际问题中有许多应用，下面介绍几个例子。

1. 数值解微分方程微分方程在物理、工程、生物学等领域中占有重要地位，但是大部分微分方程并不能求解得到。

通过数值方法来求解微分方程是一种很有效的方法，其中牛顿迭代法就是一个常用的工具。

将微分方程通过拉格朗日插值法或泰勒级数进行近似，再使用牛顿迭代法求解即可。

高斯牛顿法●问题描述：高斯牛顿法用于进行非线性最小二乘法拟合，即无约束最优化问题n是变量数目，目标函数f(x)是由m个辅助剩余函数定义r(x)，最小二乘化就是要得到剩余函数平方和的最小值。

很多最优化的问题都是最小二乘法进行最小估计的问题。

下面看一个例子：上述函数是以t为自变量，y为函数值，t为年，y为人口数目；那么剩余函数就是我们所要构建的模型函数与实际函数的差值。

假设人口增长符合指数分布，那么令：那么剩余函数就是：●几何描述：最小化的问题就是求解上述函数平方和的最小值。

若把r看做是一个向量，可以得到：这个问题就可以引申为寻找Rn中点x1和x2来得到模型函数，而且这个点对应在Rm中的曲线是最接近函数原始值的。

●Gradient and Hessian⏹Gradient是这样定义的：雅克比矩阵：在向量微积分中，雅可比矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。

雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。

因此，雅可比矩阵类似于多元函数的导数。

⏹Hessian是这样定义的：Hessian由两个函数决定，J(x)是一阶偏导数，Q(x)是二阶偏导数。

对于之前提到的那个应用问题：Hessian是两个部分的和若r(x)=0，则Q(x)=0，那么结果就会比较接近；高斯牛顿方法就是用来近似逼近使Q(x)=0，使用如下公式：如果假设J(X)是满秩的，那么J(x)TJ(x)就是正定的，而且pGN是下降收敛。

否则上式就无法得到收敛的结果。

假设r(x)用线性泰勒函数展开近似为：前面的公式就可以改变为：那么高斯牛顿线性逼近就如上图，即寻找O点距离模型图距离最近的点，也就是rk，那么就是这条直线与模型的切线。

那么与原来的牛顿方法进行比较：若f(x)=0,即Q(x)=0，那么高斯牛顿方法就和普通的牛顿方法一样收敛，如果J(x)是满秩的话；比牛顿方法优秀的地方在于不用计算二阶导数，省去了计算量；如果二阶导数值较大，那么高斯牛顿迭代的速度比普通的牛顿方法要慢；对于有些使用高斯牛顿方法局部不收敛的问题，如果没有一个好的全局策略，那么高斯牛顿都不会收敛，不管我们初始化的值距离收敛值多近。