当前位置：文档之家 › 第三章 分析力学基础 (理论力学Ⅱ)

第三章 分析力学基础 (理论力学Ⅱ)

  • 格式：ppt
  • 大小：1.87 MB
  • 文档页数：60

下载文档原格式

  / 60

合集下载

[物理]分析力学基础

[物理]分析力学基础

若主动力为有势力，须将势能 V 表示为广义坐标的函数。
4. 建立拉氏方程并加以整理，得出N个二阶常微分方程。
5. 求出上述一组微分方程的积分。
质量为m1、半径 为 r 的均质圆轮在水平面 上纯滚，轮心与刚性系数 为k 的弹簧相连。均质杆 AB长度为l ，质量为m2 。 求：系统的运动微分方程。 解：1、系统的约束为完整约束， 主动力为有势力。
V Qk 0 qk
d T T V ( ) 0 k dt q qk qk
称为拉格朗日函数（动势）
引入
L T V
因为势能只是广义坐标的函数，故
d L k dt q
L 0 q k
此即为主动力为有势 力的拉格朗日方程。
于是，虚位移原理的表达式成为
V 0
上式说明，在势力场中，具有理想约束的质点系的平 衡条件为质点系的势能在平衡位置处一阶变分为零。 如果用广义坐标 q1，q2， ，qN 表示质点系的位置, 则质点系的势能可以写成广义坐标的函数，即
V V q1，q2， ，qN
根据广义力表达式，在势力场中可将广义力 QN 写成 用势能表达的形式，即
V Qk 0 (k 1， 2， ，N ) qk
在势力场中具有理想约束的质点系的平衡条件 是势能对于每个广义坐标的偏导数分别等于零。
杆OA和AB以铰链相 连，O端悬挂于圆柱铰链
上，杆长OA=a ， AB=b
。杆重和铰链的摩擦都忽
略不计。今在点A和B分
别作用向下的铅锤力 FA 和 FB ，又在点B作用一 水平力 F 。试求平衡时 j1，j 2 与 F ，FA，FB
3、用广义坐标表示虚位移——广义虚位移
ri ri q1 , q2 ,, qN , t i 1,2, ,n
理论力学-分析力学

理论力学-分析力学

分析力学
分析力学
约束、自由度和广义坐标 虚功原理 拉格朗日方程 拉格朗日方程的应用举例 微震动 哈密顿函数和正则方程 哈密顿原理和正则变换 不变环面和KAM定理
√
约束、自由度和广义坐标(1/9)
为什么要分析力学
牛顿力学的困难 表述麻烦：例如球坐标系中的运动方程 约束力/约束关系：增加求解方程的难度和复杂性
约束、自由度和广义坐标(3/9)
约束方程 设质点组各质点的位置是 有 k 个约束
，速度是
对于一个具有 n 个质点的体系，如果存在 k 个约束(方 程)，那么在确定体系位形变化的 3n 个坐标参量中， 只有 3n - k = s 个参量可以独立变化
例：水分子体系的位形？ 无约束——水蒸气，有约束——冰
√
虚功原理(8/13) 平衡方程
√
虚功原理(11/13)
例：长分别为 l1 和 l2 轻绳(AC 和 BC， ACB=90)，悬挂重量为 W 的重物，
求张力 T1 和 T2 的大小
虚功原理
，未知坐标和不定乘子
张力 T1 和 T2 的大小
√
虚功原理(பைடு நூலகம்2/13)
势场中质点组的平衡条件和稳定性条件
虚功原理的广义坐标表述和广义力
广义坐标表述虚功原理，广义力
称 Q 为广义力，Qa 为广义力在 a 方向上的分量
当广义坐标 qa 是线量时，相应的广义力 Qa 是力的分 量；当广义坐标是角量时，相应广义力是力矩的分量
平衡状态下 Qa (q1, …, qs;t) = 0, (a = 1, …, s)
平衡条件：在理想约束条件下，主动力是保守力的力学系 平衡的充分必要条件是，质点组势能函数对每个广义坐标 的偏导数等于零
第3章分析力学基础-文档资料

第3章分析力学基础-文档资料



V F iy yi
F iz

V zi
V V V ( x y z V i i i) x y z i i i

Nn

n n x y z i i i F F F 设： Q k ix iy iz q q q i 1 1 1 k i k i k n
则：
W Q q 0
F k 1 k k
N
q k :
Qk :
为广义虚位移
称为广义力 δk为线位移， Qk 量纲是力的量纲； δk为角位移， Qk 量纲是力矩的量纲。




同理：
yi zi

N
N
k 1
yi qk q k zi qk q k
k 1
q k 为广义虚位移。虚位移用广义坐标表示。
×
§ 3-2 以广义坐标表示的质点系平衡条件
在虚位移原理中，以质点直角坐标的变分表示虚位移。 这些虚位移通常不独立，需要建立虚位移之间的关系。 若直接用广义坐标变分来表示虚位移，广义虚位移之间相互独 立，虚位移原理可表示为简洁形式。
n W F r ( F x F y F z ) i i ix i iy i iz i F n i 1 i 1
n N N N
xi

N
k 1 N
xi q qk yi q qk zi q qk
k
x y z yi i i i ( F q F q F q ) i x k i y k i z k q q q i 1 k 1 k k 1 k k 1 k
理论力学II-PPT课件

理论力学II-PPT课件


上式中令 Qk
F i
i 1
n
r i qk
Qk 为系统对应于广义坐标qk 的广义力. ( k = 1、2、3……N )
所以,
F r Q q 0
i i i 1 k 1 k k
n
N
由于各广义坐标是互相独立的, 而虚位移是不能为零的. 因而有:
Q Q Q Q 0 1 2 3 N
理论力学 ( II )
第 三 章
分析力学基础
自由度和广义坐标是分析力学最基本的概念. 虚位移原理的广义坐标描述便是: 对应于各广 义坐标的广义力分别为零是系统静止平衡的充 要条件. 虚位移原理也称静力学普遍方程.虚位 移原理与达朗伯原理的结合便得到动力学普遍 方程. 动力学普遍方程的广义坐标表达可得到 拉格朗日方程. 确切地说是第二类拉格朗日方 程.它是完整约束下的质点系统的运动微分方 程通式.
n
则
F r Q q w
i i i 1 k 1 k k k 1 k
n
N
N
称Qk 为系统对应于广义坐标qk 的广义力. ( k = 1、2、3……N ) 广义力的求法: (1) 在直角坐标系下
x y z i i i Q (F F F ) k ix iy iz q q q i 1 k k k
FB
§3 – 2 以广义坐标表示的质点系的平衡条件
由虚位移原理:
n
Fi ri 0
i 1 n
n
及
r ri i qk k1 qk
N
N n r r i i F r F q F q 0 i i i k k q q i 1 i 1 k 1 k 1 i1 k k N
理论力学3分析力学基础课后答案

理论力学3分析力学基础课后答案


代入拉格朗日方程，得
则 3-3
[
]
质量为 m 的质点悬在 1 线上，线的另 1 端绕在 1 半径为 R 的固定圆柱体上，如图
250
3-3 所示。设在平衡位置时，线的下垂部分长度为 l，且不计线的 质量。求此摆的运动微分方程。 解 取 θ 为广义坐标，设小球的静平衡位置为其零势能点。 系统势能
V = mg [(l + R sin θ ) − (l + θR ) cosθ ]
A
A x
& & x
θ
C
θ
FN
ϕ
θ −ϕ
l & ϕ 2 y
θ
& & x
θ
x′ B
C mg B
(c)
l && ϕ 2 y
(a)
& （见图 3-7b） & 、ϕ 解 2 自由度，给广义坐标 x， ϕ ，则广义速度为 x
(b) 图 3-7
l & & − cos(θ − ϕ )ϕ vCx = x 2 l & sin(θ − ϕ ) vCy = ϕ 2
x A = x B = 0, y A = −2a sin θ ， y B = 2a sin θ , xO = 2a cosθ
对相应坐标的变分
δ x A = δ x B = 0,δ y A = −2a cosθδ θ ,δ y B = 2a cosθδ θ δ xO = −2a sin θδ θ
根据动力学普遍方程，有
系统动能
势能
m 2 m 2 l2 2 m 1 m 2 & 2 = (x & + ϕ & − lx &ϕ & cos(θ − ϕ )) + l 2ϕ &2 (vCx + vCy ) + ⋅ l 2ϕ 2 2 12 2 4 24 m 2 m 2 2 m & + lϕ & − lx &ϕ & cos(θ − ϕ ) = x 2 6 2 l V = − mgx sin θ − mg cos ϕ （设初始 A 处势能为零） 2 T= ∂L m & cos(θ − ϕ ) & − lϕ = mx & ∂x 2 d ∂L m m && cos(θ − ϕ ) − lϕ & sin(θ − ϕ )ϕ & & − lϕ ( ) = m& x & dt ∂x 2 2
lxy理论力学(II)分析力学基础

lxy理论力学(II)分析力学基础


写成解析表达式
n
((Fxi mi xi )δxi (Fyi mi yi )δyi (Fzi mi zi )δzi ) 0
i 1
——动力学普遍方程
特别适合于求解非自由质点系的动力学问题。
例 1－4
已知：滑轮系统中，动滑轮上悬挂着质量为 m1 的 重物，绳子绕过定滑轮后悬挂着质量为 m2
δ1
δ1
Q1 (FA FB )a sin1 Fa cos1
保持 1不变， 只有 2 时
可得另一组虚位移
δyA 0
δyB b sin2δ2
δxB b cos2δ2
对应于 2 的广义力
Q2
δW2 FAδyA FBδyB FδxB
Qk

n
(Fxi
i1
xi qk
Fyi
yi qk
Fzi
zi ) qk
(k 1，2，，N)
Q1 Q2

FA FA
y A
1
y A
2
FB FB
y B
1
y B
2
F xB
1
F xB
2

yA a cos1 yB a cos1 b cos2 ，xB a sin1 bsin2
思考：
非完整约束，广义坐标数目和系统的自由度数目的关系？
设由n个质点组成的系统受s个完整双侧约束
约束方程为
fk (r1 ，r2 ,，rn ，t) 0
(k 1，2 ，3，，s)
系统N个独立的坐标参量表示为
q1 ，q2 ，，qN
(N 3n s)
拉格朗日广义坐标
理论力学2

理论力学2


大小
M=+F.d
逆正顺负
正负号
+
-
力偶对物体的作用效应取决于： A 力偶矩的大小 B 力偶矩的方向
25
二、力偶的性质
性质一
力偶既没有合力，也不能和一个力平衡
力偶对物体的作用效果不能用一个力来代替 力偶必须用力偶来平衡
26
性质二
力偶对其作用面内任意一点的矩恒等 于该 力偶的力矩，与矩心的位置无关。
， 选投影轴列方程为

=？ 地面的反力ND=？
X 0
T2cos T10 ①
Y 0
由①得
T2 sin Q N D 0
②
1 cos T P 1 T2 2P 2
600
0
由②得
ND Q-T2sin Q-2Psin 60 Q 3P
15
[例] 求当F力达到多大时，球离开地面？已知P、R、h
解：研究块,受力如图，
解力三角形： 又：
N F cos
R2 (R h)2 1 cos h(2R h) R R
F R N h ( 2 R h)
16
再研究球，受力如图：
作力三角形
解力三角形：
P N sin 又sin R h R
F1 R sin sin( 180 )
根据图形的边角关系，用三角公式计算出所要求的未 知量，这种解题方法为几何法。
6
[例] 已知压路机碾子重P=20kN, r=60cm, 欲拉过h=8cm的障碍物。
求：在中心作用的水平力F的大小和碾子对障碍物的压力。
解： ①选碾子为研究对象
②取分离体画受力图 ∵当碾子刚离地面时NA=0,拉力F最大,这时 由平衡的几何条件，力多边形封闭，故
理论力学训练题集新参考答案

理论力学训练题集新参考答案

参考答案 第一章一、1、① 2、③ 3、④ 4、②二、1、 90° 2、等值、反向、共线 3、120°；0 4、略。

第二章一、1、④ 2、② 3、① 4、②、② 5、②、④ 6、①、②7、② 9、② 10、① 11、③、① 12、② 二、1、2P ，向上 2、2P,向上 3、0°，90°4、可以，AB 两点不与汇交点O 共线5、通过B 点的一合力，简化为一力偶6、10 kN ，向左7、L m 3/348、α2cos 1m第三章一、1、② 2、③ 3、③ 4、④ 5、② 二、1、P ，-P ，P ，0，0，0 2、0，am2 3、二矩心连线不垂直投影轴4、0，-P5、为一合力，为一力偶，平衡 三、110=kN 3NB F 110=kN,=100kN,=03Ax Ay A F F M 四、=2Dx F KN ；=0Dy F KN ；=2Fx F KN ；=0Fy F KN 五、N F AX 350=，N F AY 100=，N F DX 850=，N F DY 900= 六、a M F C /=，a M F AX /=，0=AY F ，M M A -=第四章一、1、④ 2、② 3、④ 4、③ 5、④ 二、1、'=R F P ，=-ai+bj A M P P 2、F c b a ba 222++-3、①力偶矩的大小；②力偶作用面的方位；③力偶的转向。

4、力偶5、2,3；1,3；2,3；3,6。

三、主矢：250='RF ，主矢方向：21cos 0cos 21cos ===γβα主矩 ＭＢ＝2.5Ｎm ，主矩方向：0cos 0cos 1cos ===γβα四、kN F F kN F O z O y O x 6015===，，；m kN M m kN M m kN M O z O y O x ⋅-=⋅=⋅=502458，，第五章一、1、② 2、①，①，① 3、① 4、③ 5、③ 二、1、2φm 2、F=0,m ＝3N·cm 3、F ＝15KN 4、F=P,M=PR 5、翻倒，T=0.6839P 三、θφan /12an t t += 四、系统处于静止状态。

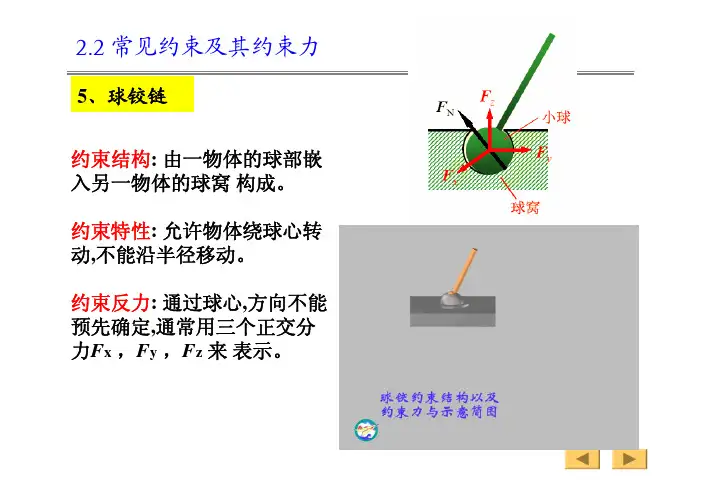
理论力学课件 受力分析与受力图、第三章

理论力学课件 受力分析与受力图、第三章

5、球铰链
约束结构: 由一物体的球部嵌入另一物体的球窝构成。

约束特性: 允许物体绕球心转动,不能沿半径移动。

约束反力: 通过球心,方向不能预先确定,通常用三个正交分力F x，F y，F z来表示。

人造髋关节
二力杆工程实例
固定端约束除了加约束力，还要加上约束力偶。

运动学角度：固定端既限制线位移，又限制角位移，如果只有约束力，则构件将转动。

必须有约束力偶才行。

力系简化角度：固定端所受的力是一个复杂的平面任意力系，力系向端部某点简化的结果是一力和一力偶。

CD是不是二力
杆？
2.3 受力分析与受力图
刚化原理：若变形体在某一力系作用下处于平衡，则将此变形体刚化为刚体，其平衡状态保持不变。

只有刚化原理没有软化原理。

1. 右拱BC 的受力图。

C
B
解：
F C
F B
2. 左拱AC 的受力图。

A C
F
F Ax C F
F Ay。

【理论力学2】第三章分析力学基础

【理论力学2】第三章分析力学基础


n xi yi z i ( Fxi Fyi Fzi )q k 0 q k q k q k k 1 i 1
（3－6）
如令
Qk ( Fxi
i 1 n
xi y z Fyi i Fzi i ) (k 1 ， 2， ，N ) （3－7） qk qk qk
如图所示
由式（b）的变分
可得一组虚位移 y A y B a sin 11 ，xB a cos11 则对应于 1的广义力为
Q1
（e ）
W1 FAy A Fy B Fx B 1 1
将式（e）代入上式 得 保持 1不变 只有2 时 如图所示 由式（b）的变分 可得另一组虚位移 y A 0 ，y B b sin 2 2 ，xB b cos 2 2 代入对应于 2 的广义力表达式 得
W A FAx A PC yC ( FA PC )x A
对应广义坐标 x A 的广义力为 WA 1 QxA PC FA x A 2
1 2
（a）
再令y B向下 x A 0
同理可解得 （b）
1 PC 2 P ，FA PC P 2 因此平衡时 要求物块与台面间静摩擦因数 FA f 0.5 2P 如果作用在质点系上的主动力都是有势力 则势能应为各点坐标的函数 记为
（3－13）
这样 由广义坐标表示的平衡条件可写成如下形式 V Qk 0 (k 1 ， 2， ，N ) （3－14） qk 即 在势力场中具有理想约束的质点系的平衡条件是势能对于 每个广义坐标的偏导数分别等于零 稳定平衡 不稳定平衡 在稳定平衡的平衡位置处 系统势能具有极小值 在不平衡位置上 系统势能具有极大值 对于随遇平衡 系统在某位置附近其势能是不变的 所以其附近任何可能位置都是平衡位置
分析力学基础达朗贝尔原理

分析力学基础达朗贝尔原理


FAy 2mg
FAx

mw 2b2
l
sin 2
F2*

a2

P2
FAx
x
b
mg
A
FAy
M * mw2b2 sin 2
由于平面x-y随轴AB一起转动，所以轴承受
2019年7到月2的5日力在惯性基上观察是在不断的改变方向
17 理论力学CAI 分析力学基础
分析力学基础/达朗贝尔原理/惯性力质点系达朗贝尔原理/例

v FT
小球平衡方程
： Fy* cos Fx* sin mg sin 0
Fy*
x
(l0 vt) 2v g sin 0
小球动力学方程
2019年7月25日 理论力学CAI 分析力学基础
y

Fx*
ax
ay

mg
20
分析力学基础/达朗贝尔原理
达朗贝尔原理
• 前言 • 达朗贝尔惯性力与质点系达朗贝尔原理 • 一般运动刚体的动静法 • 平面运动刚体的动静法 • 定轴转动刚体的动静法 动反力
2019年7月25日 21
理论力学CAI 分析力学基础
分析力学基础/达朗贝尔原理/一般运动刚体动静法
一般运动刚体动静法
• 刚体的达朗贝尔原理 • 刚体达朗贝尔惯性力的简化
O
x (l0 vt) cos y (l0 vt) sin

小球加速度
ax x (l0 vt)sin (l0 vt) 2 cos 2v sin
v
FT
ay y (l0 vt) cos (l0 vt) 2 sin 2v cos

理论力学(2)终版.ppt

0.0
P = 100 N
P
y
25
阅读材料和作业
• 阅读材料
– (1)P53---P65; P150---P162
– (2)P64---P83 • 作业
– (1)2---31 ; 2---34 ;4---4
– (2)3---6; 3---15; 3---20 • 预习内容
– (1)P83---P91
– (2)P95---P114
0.0
26
再见
0.0
27
=-bSi-aSj
mix = 0
D
Q
C
x
P
bQ-bS=0
(1)
miy = 0
b
aP-aS=0
(2)
P
联立(1)(2)两式得: 0.0
P 1 Q
S=P
23
例题3-5. 若三个力偶作用于楔块上使其保 持平衡.设Q = Q=150N.求力P与F的大小.
z
F´
FQ
o
P
y
0.3m
Q´
x
0.4m
P´
0.0
理论力学
(2)
0.0
1
内容提要
三.力偶理论
3-1.力对点的矩 3-2.两平行力的合成 3-3.力偶与力偶矩 3-4.力偶的等效条件 3-5.力偶系的合成与平衡
0.0
2
3-1.力对点的矩
z
B
(1)力对点的矩
mo(F)
F
mo(F) = r×F
A
mo(F)表示力F绕O点
O
r
y
转动的效应.O点称为矩
d
x
0.0
A
F´ rA

(II) 第一章 分析力学基础

2009年12月29日第一章分析力学基础第一章分析力学基础经典力学本章内容：§1–5 拉格朗日方程的初积分§1–6 第一类拉格朗日方程以广义坐标表示的质点系平衡条件一、以广义坐标表示的虚功方程虚功方程广义坐标ii++i zi i yi iF F的广义力广义虚位移δq k ++izi i yi i F F即：二、广义力的计算δq≠0kz z z δqk≠0[例1-1] 求广义力A BC M x ϕoδx δr C m 1gm 2g解：0δ,0δ=≠ϕx （1）求Q xδθA BC M x ϕom 1gm 2gδϕδr C（2）求Q ϕϕδ,0δ=≠ϕx （1）求Q x0δ,0δ≠=ϕx三、有势力的广义力元功元功元功推广：y x dd−−广义坐标当质点系所受的主动力都是有势力时，有广义力++i zi i yi iF F当质点系所受的主动力都是有势力时，有广义力++i zi i yi iF F四、势能驻值定理变分虚位移原理主动力i i i即：有势力驻值五、最小势能原理稳定性稳定五、最小势能原理稳定性随遇平衡结论：稳定最小势能原理¾¾z达朗贝尔原理z虚位移原理达朗贝尔原理虚位移原理即：动力与惯性力在该系统的任意虚位移上的虚功之和为零。

动力学普遍方程解析形式即：动力学普遍方程[例1-2]已知：解：求：C 2C 1θAC Bza 1a ea rαF I1F I2eF I2r M I2αR a =rC 2C 1θA CBF I1F I2e F I2r M I2m 1g m 2g zδ,0δ≠=ϕx x ϕδx ¾δr C2δϕC 2C 1θA CBF I1F I2eF I2r M I2δx δϕm 1gm 2gcos (1−a θ0δ,0δ=≠ϕx ¾=δx121121cos (1−a θ本章内容：§1–5 拉格朗日方程的初积分§1–6 第一类拉格朗日方程上次内容回顾：广义力：广义坐标广义坐标注意动力学普遍方程广义坐标下面对第二项用广义坐标iiii广义惯性力动力学普遍方程广义惯性力广义惯性力：i i&=i i =)(在完整约束下，第t i∂∂+r k ki q q &∂∂r 广义速度i &r ii i =)(i i(i i (ii(i ii ii(i i广义惯性力⋅(i i r &⋅i i i i ⋅(i (ii ⋅r &(i=)(i i &&⋅r i &i ⋅i i (kii ⋅r &(k i i i &∂=⋅i i i ⋅i i (i &i (i im &∑i i m((i i m &∑i i m (第二类拉格朗日方程z有势力第二类拉格朗日方程−)((−)拉格朗日函数(−)保守系统z自由度广义坐标思考：(广义力。

《分析力学基础》课件

容
哈密顿-雅可比 方程可以描述 系统的运动状 态和能量变化
哈密顿-雅可比 方程在分析力 学中具有重要
地位
正则方程的定义和性 质
正则方程的求解方法
正则方程在分析力学 中的应用
正则方程与拉格朗日 方程的关系
正则方程在工程中的 应用实例
课件结构
● 引言：介绍分析力学的基本概念和重要性 ● 第一部分：牛顿力学 ● 牛顿三定律 ● 动量守恒定律 ● 角动量守恒定律 第二部分：拉格朗日力学
弹性模量：描述固体材料弹 性性质的物理量
胡克定律：描述固体材料在弹 性范围内的应力与应变关系
泊松比：描述固体材料在弹性 范围内的横向应变与纵向应变
的关系
弹性力学基本方程：描述固体 材料在弹性范围内的应力、应
变和位移之间的关系
哈密顿原理：描述系统演化的普遍 规律，适用于经典力学和量子力学
哈密顿原理的应用：求解力学问题， 如求解运动方程、求解哈密顿量等
分析力学基础PPT课 件大纲
汇报人：
目录
添加目录标题
课件简介
课件内容
课件结构
课件效果
课件使用说明
添加章节标题研究物体在力作用下的运动规律
课件旨在帮助学生理解分析力学的基本概念、原理和方法
课件适用于物理专业学生、教师和相关研究人员
课件内容涵盖了分析力学的主要内容，包括牛顿力学、拉格朗日力学和哈密顿力 学等
页脚：包括作者、日期、版权等信息
背景：选择与主题相关的背景图片或颜 色
课件效果
课件内容：包括基 本概念、原理、公 式、应用等
教学方法：采用案 例分析、实验演示、 互动讨论等方式
学习效果：提高分 析力学知识水平， 增强解决问题的能 力
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

yi qk
Fzi
zi ) qk
(k 1，2，，N) （3－7）
则式（3－6）可以写成
N
WF Qkqk 0
k 1
上式中 Qkqk 具有功的量纲
所以称Qk为与广义坐标qk 相对应的广义力
由于广义坐标的独立性 qk可以任一取值
因此若式（3－8）成立 必须有
（3－8）
Q1 Q2 QN 0
yA yB a sin1 1 ，xB a cos1 1
则对应于 1的广义力为
Q1
W1 FAy A FyB FxB
1
1
（e）
将式（e）代入上式 得
保持 1不变 只有 2 时
如图所示
Q1 (FA FB )a sin1 Fa cos1
由式（b）的变分
可得另一组虚位移
yA 0，yB b sin2 2 ，xB b cos2 2
代入对应于 2 的广义力表达式 得
Q2
W2 FAy A FByB FxB
2
2
FBb sin 2 Fbcos2
例 3－2
如图所示 重物A和B分别连接在细绳两端
重物A放置在粗糙的水平面上
重物B绕过定滑轮E铅直悬挂
在设动重滑物轮A重H量的为轴心2P上挂一重物C 重物B重量为P
不计动滑轮H的重量
（3－9）
上式说明
质点系的平衡条件是系统所有的广义力都等于零
这就是用广义坐标表示的质点系的平衡条件
求广义力的方法有两种
一种方法是直接从定义式（3－7）出发进行计算
另一种是利用广义虚位移的任意性 令某一个qk 不等于零 而其他N-1个广义虚位移都等于零 代入
从而
WF Qkqk
Qk
WF qk
（3－10）
将式（3－5）代入虚功方程 得到
WF
n
WFi
i1
n i1
(Fxi
N k 1
xi qk
qk
Fyi
N k 1
yi qk
qk
Fzi
N k 1
zi qk
qk
)
N n
(Fxi k 1 i1
xi qk
Fyi
yi qk
Fzi
zi qk
)qk
0
（3－6）
如令
Qk
n
(Fxi
i1
xi qk
Fyi
第三章 分析力学基础
§ 3－1 自由度和广义坐标
在完整约束的条件下 确定质点系位置的独立参数的数目等于系统的自由度数
例如质点M被限定只能在球面
(x a)2 ( y b)2 (z c)2 R2
的上半部分运动 由此解出
（3－1）
z c R2 (x a)2 ( y b)2
（3－2）
对于完整系统 广义坐标的数目等于系统的自由度数
考虑由nfk个(r1质，点r2组 成，的rn ，系t统) 受0 s个完(k整 双1，2，侧3，约 ， 束s) （3－3）
设 q1 ，q2 ， ，qN (N 3n s) 为系统的一组广义坐标
我们可ri以将ri (各q1质，点q2 的 ， 坐q标N 表，示t) 为 (i 1，2， ，n) （3－4）
( V xi
xi
V yi
yi
V zi
zi )
V
虚位移原理的表达式成为
V 0
（3－12）
上式说明：在势力场中 具有理想约束的质点系的平衡条件为质点系的势能在平 衡位置处一阶变分为零 如果用广义坐标q1，q2， ，qN 表示质点系的位置 则质点系的势能可以写成广义坐标的函数 即
由虚位移的定义 对上式进行变分运算 得到
ri
N k 1
qrik qk
(i 1，2， ，n)
（3－5）
其中 qk (k 1，2， ，N )为广义坐标qk 的变分 称为广义虚位移
§ 3－2 以广义坐标表示的质点系平衡条件
设作用在第i个质点上的主动力的合力Fi 在三个坐标轴上的投影分别为(Fxi ，Fyi Fzi )
试求平衡时重物C的重量
PC
以及重物A与水平面间的静滑动摩擦因数
解： 系统具有两个自由度
选取重物A向右的水平坐标 x A
和重物B向下的铅直坐标 yB为广义坐标
则对应的虚位移为
x
A
和y
B
此时除重力外
重物A与台面间的摩擦力 FA 也应视为主动力
首先令 x A 向右 yB 0
此时重物C的虚位移yC xA / 2 方向向下
在解决实际问题时 往往采用第二种方法比较方便
例 3－1
杆OA和AB以铰链相连 O端悬挂于圆柱铰链上
如图所示 杆长OA=a AB=b
杆重和铰链的摩擦都忽略不计
今又试在在求点点 平A衡B和作时B用分一1，别水作2平与用力F向AF下，F的B ，铅F锤之力间F的A和关系FB
解： 系统有两个自由度 现选择 1 和 2 为系统的两个广义坐标 计算其对应的广义力Q1和 Q2 用第一种方法计算：
这样该质点在空间中的位置就由x,y这两个独立参数所确定 它的自由度数为2 一般来讲 一个n个质点组成的质点系 若受到s个完整约束作用 则其在空间中的3n个坐标不是彼此独立的
由这些约束方程
可将其中s个坐标表示成其余3n-s个坐标的函数
这样该质点系在空间中的位置
就可以用N=3n-s个独立参数完全确定下来 描述质点系在空间中的位置的独立参数 称为广义坐标
主动力所做虚功的和为
WA
FAx A
PCyC
(FA
1 2
PC
)x
A
对应广义坐标 xA 的广义力为
QxA
WA x A
1 2
PC
FA
（a）
再令yB向下 xA 0 同理可解得
QyB
WB xB
1 2
PC
P
因为系统平衡时应有 QxA QyB 0 解得
PC
2P ，FA
1 2 PC
P
因此平衡时 要求物块与台面间静摩擦因数
由于
Q1
FA
y A
1
FB
y B
1
F xB
1
Q2
FA
y A
2
FB
y B
2
F
xB
2
（a）
yA a cos1 ，yB a cos1 b cos2 ，xB a sin1 bsin（2 b）
故
y A
1
a
sin
1
，y B
1
a
sin
1
，xB
1
a cos1
y A
2
0 ，yB
2
b
sin
2
，xB
2
b cos2Βιβλιοθήκη 代入式（a） 系统平衡时应有
解出
Q1 Q2
(FA FB )a sin1 Facos1 FBb sin2 Fbcos2 0
0
tan 1
FA
F
FB
，tan 2
F FB
（c） （d）
用第二种方法计算：
保持 2 不变
只有 1时 如图所示
由式（b）的变分 可得一组虚位移
（b）
f FA 0.5 2P
如果作用在质点系上的主动力都是有势力
则势能应为各点坐标的函数 记为
V V (x1，y1，z1， ，xB，yB，zB ) （3－11）
此时虚功方程（3－6）中各力的投影 都可以写成用势能V表达的形式 即
于是有
Fxi
V xi
，Fyi
V yi
，Fzi
V zi
这样
WF (Fxixi Fyiyi Fzizi )