黑龙江省大庆市肇源县第四中学2019--2020期中测试题初四数学试题
- 格式:docx
- 大小:149.20 KB
- 文档页数:5
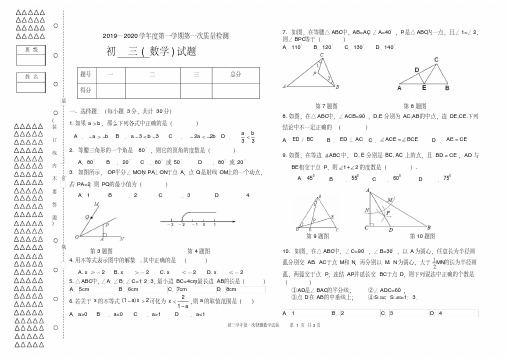
初一数学 共三页 (1)初四年级数学试卷考生注意:1、考试时间为120分钟题分 一 二 三总分 得分1920 2122232425262728一、 选择题 (10x3分=30分)1.数据4.36⨯10-4所表示的小数为()A 0.0436 B0.00436 C 0.000436 D 0.0000436 2.-2019的绝对值是( )。
A 20191-B 2019±C 20191D 20193.函数xxy 21-=的自变量x 的取值范围是 ( ) A 21≠x B 021≠≤x x 且 C 21≤x D x 0≠ 4 .平面直角坐标系中的点P (m-3,4-2m )不可能在( )A 第一象限B 第二象限C 第三象限D 第四象限 5. 大庆市5月份某一周每天的最高气温统计如下表, 则这组数据的中位数和平均数分别是 ( )温度/o C 2224 26 29 天数2 13 1 6. 一个用相同的小立方块搭成的几何体的三视图如下图, 则组成这个几何体的小立方块的个数是( )A 2B 3C 4D 57. 一次函数y=ax+b 和反比例函数xcy =在同一 平面直角坐标系中的图像如图所示,则二次函数c bx ax y ++=2的图像可能是( )A B C D8. 如图,AD 是ΔABC 中∠BAC 的平分线, DE ⊥AB 于点E ,DE=2,AC=3,则ΔADC 的 面积是()A 3B 4C 5D 69. 已知一元二次方程01222=-+x x 的两个根为为x 1,x 2且x 1<x 2, 下列结论正确的是 ()A x 1+x 2=1B x 1x 2=-1C |x 1| <|x 2|D x 12+x 1=21 10. 如图,抛物线)0(2≠++=a c bx ax y 的对称轴为x=-1,与x 轴的一个交点在(-3,0)和(-2,0)之间,其部分图像 如图所示,则下列结论:①abc>0 ②b 2-4ac>0③2a=b,④点),45(),,23(),,27(321y y y --是抛物线上的点,则y 1<y 2<y 3,⑤3b+2c<0⑥t(at+b)≤a-b(t 为任意实数) 其中正确的个数()A 3B 4C 5D 6ΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔ姓 名班 级ΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔ装订线初一数学 共三页 (2)二、填空题 (8x3分=24分)11.若==-bb a a a32,则 ____ 。

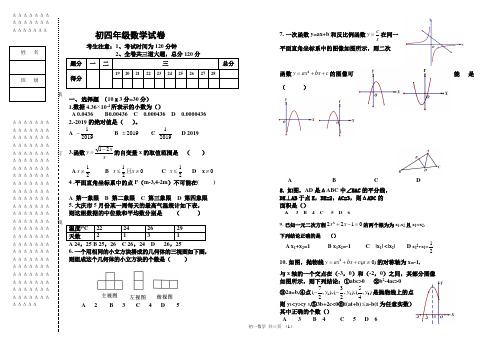
2019---2020学年度第一次月考初四数学试题考生注意:1、考试时间为120分钟2、全卷共三道大题,总分120分一、1.在Rt ABC △中,90C ∠=︒,若2AC BC =,则sin A 的值是() A.12 B.2 2.在Rt ABC △中,90C ∠=︒,若4AB =,3sin 5A =,则斜边上的高等于() A.6425 B.4825 C.165 D.1253.在ABC △中,若cos A =tan BA.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形 4.抛物线y=x 2+bx+c 图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x 2﹣2x ﹣3,则b 、c 的值为( ) A. b=2,c=2 B. b=2,c=0 C. b=﹣2,c=﹣1 D. b=﹣3,c=2 5.对于二次函数y =-x 2+x -6,下列说法错误的是( ) A 当x=时,y 有最大值 B 图像的顶点坐标( ) C 图像与x 轴有两个交点D x <0时y 随x 的增大而增大6.若A ⎝ ⎛⎭⎪⎫34,y 1,B ⎝ ⎛⎭⎪⎫-54,y 2,C ⎝ ⎛⎭⎪⎫14,y 3为二次函数y =x 2+4x -5的图象上的三点,则y 1,y 2,y 3的大小关系是( )A .y 1>y 2>y 3 B .y 2>y 1>y 3 C .y 3>y 1>y 2 D .y 1>y 3>y 27.如图,轮船从B 处以每小时60海里的速度沿南偏东20°方向匀速航行,在B 处观测灯塔A 位于南偏东50°方向上,轮船航行40分钟到达C 处,在C 处观测灯塔A 位于北偏东10°方向上,则C 处与灯塔A 的距离是( )A.20海里B.40海里C.2033海里D.4033海里8把一块含45°角的直角三角板ODE 放在如图所示的平面直角坐标系中,已知动点P 在斜边OD 上运动,点A 的坐标为(0,2),当线段AP 最短时,点P 的坐标为( )A.(0,0)B.(22,22) C.(12,12) D.(12,22) 9如图,水库大坝的横断面积为梯形,坝顶宽6米、坝高4米、斜坡AB 的坡角为45°,斜坡CD 的坡度i =1∶2,则坝底AD 的长为 ( ) A . 24米 B .20米 C .18米D .38米10.二次函数y=ax 2+bx+c (a ≠0)的部分图象如图③所示,,对称轴为直线x=2,则下列结论中正确的个数有( ) ①4a+b=0; ②9a+3b+c <0; ③a-b+c >0 ④若点A(﹣3,y 1),点B (﹣ ,y 2),点C (5,y 3)在该函数图象上,则y 1<y 3<y 2;A 1个 B2个 C3个 D4个考 号姓 名(装订线内 不要答题 )本考场试卷序号(由监考教师填写)二、填空11.1)3(232++-=+-kx x k y k k,是二次函数,则k 的值是_________12. 如图,在Rt △ABC 中,∠C =90°,D 是AB 的中点,ED ⊥AB 交AC 于点E.设∠A =α,且tan α=13,则tan 2α=________.13.周长为20的等腰三角形,一边长为8,则底角的余弦值为______. 14.已知锐角A 满足表达式2sin 2A-7sinA+3=0则sinA 的值_________15.二次函数y =x 2-x -6的图象交x 轴于A ,B 两点,交y 轴于C 点,则△ABC 的面积为________.16.已知抛物线y=2x 2-2mx+m 2+n 的顶点坐标为(2,-5)则m+n=_______,17. 某商场,服装进价的单价是20元,销售单价是30元时,月销售量是230件,而销售单价每上涨一元,月销量就减少10件,设每件玩具的销售单价上涨x,【x 为正整数】元时,月销售利润为y 元,则 y 与x 的函数表达式: .18.如图,一个小球由地面沿着坡度1:3i =的坡面向上前进了10m ,此时小球距离地面的高度为 .19.如图,从热气球C 上测得建筑物A ,B 底部的俯角分别为30°和60°,如果这时气球的高度CD 为150米,且点A ,D ,B 在同一直线上,那么建筑物A ,B 间的距离为________20.抛物线y=ax2 +c 与y=2x 2形状相同,其顶点坐标是(0,1)则其表达式_________三、计算1. 2cos45°-16+(-14)-1+(π-3.14)0.2.230116(2)(πtan60)3-⎛⎫--÷-+-︒-︒ ⎪⎝⎭22.(6分)如图,在△ABC 中,∠B =45°,AC =132,BC =10,求sinA 和AB .23.有长为24 m 的篱笆,围成中间隔有一道篱笆的长方形的花圃,花圃的长可借用一段墙体(墙体的最大可用长度a=10)设花圃的宽AB 为x m,花圃ABCD 的面积为S m 2 (1) 求S 与x 的函数关系式; (2) 如果要围成面积为45 m 2的花圃,AB 的长是多少米?24.如图,一艘油轮以240/min m 的速度向正北方向航行,行驶到A 处测得一灯塔C 在它的北偏西30小岛上,油轮继续向北航行,5min 后到达B 点,又测得灯塔C 在它的北偏西45方向,根据有关资记载,在距灯塔C 为中心1500m 范围内有暗礁.试问:这艘油轮不改变前进方向继续行驶是否有触 的危险?为什么?考 号姓 名( 装 订 线 内 不 要答题)25. 如图,某人在山坡坡脚C 处测得一座建筑物顶点A 的仰角为60°,沿山坡向上走到P 处再测得该建筑物顶点A 的仰角为45°.已知BC =90米,且B 、C 、D 在同一条直线上,山坡坡度为21(即tan ∠PCD =21).(1)求该建筑物的高度(即AB 的长). (2)求此人所在位置点P 的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)26.如图,AD 是△ABC 的中线,tan B =13,cos C =22,AC = 2.求:(1)BC 的长; (2)sin ∠ADC 的值.27如图抛物线y 1=x 2与直线y 2=x+b 的交点为A (-1,a )和点B (1) 求a,b 的值及点B 的坐标 (2)根据图像判断当x 为何值时,y 1 < y 228已知抛物线y= - 41X 2 +bx+4 与x 轴相交于A ,B 两点,与Y 轴相交于C ,若已知A 点的坐标(-2,0)(1)求抛物线的解析式及它的对称轴; (2)求点C 的坐标,连接AC 、BC 并求线段BC 所在直线的解析式;。

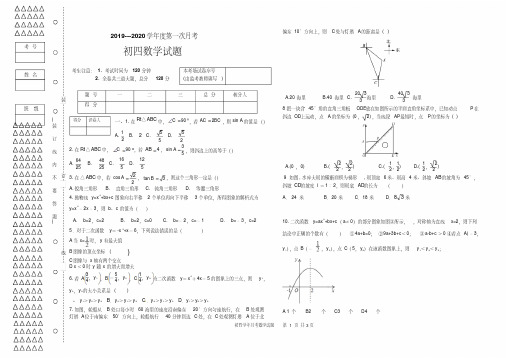
2019—2020学年度第一学期期中质量检测初四 (数学)试题一、选择题:(每小题3分,共计30分)1.抛物线y=2(x+3)2+5的顶点坐标是()A.(3,5)B.(﹣3,5)C.(3,﹣5)D.(﹣3,﹣5)2.如图,点A、B、C都在圆O上,若∠AOB=72°,则∠ACB的度数为( )A. 18°B. 30°C. 36°D. 72°3.已知⊙A半径为5,圆心A的坐标为(1,0),点P的坐标为(﹣2,4),则点P与⊙A的位置关系是()A. 点P在⊙A上B. 点P在⊙A内C. 点P在⊙A外D. 不能确定4.在△ABC中,∠C=90°,如果tanA= ,那么sinB的值等于()A. B. C. D.第2小题第5小题5.如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D﹣∠A的度数差为()A. 10°B. 15°C. 20°D. 25°6.已知抛物线y=(a+1)x2-ax-8,过点(2,-2),且与x轴的一个交点的横坐标为2n,则代数式4n2-n+2016 的值为( )A.2020B.2019C.2018D.20177.抛物线y=x2﹣2x+1与坐标轴交点个数为()A. 无交点B. 1个C. 2个D. 3个8.在直角三角形中两个锐角的正弦值的平方和为( )A. 0.5B. 1C. 2D. 2.59.如图,将Rt△ABC 形状的楔子从木桩的底端P 沿水平方向打入木桩,使木桩向上运动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6cm (如箭头所示),则木桩上升了( )A. 6sin15°cmB. 6cos15°cmC. 6tan15° cmD. cm第9小题 第10小题10.抛物线的部分图象如图所示,与x 轴的一个交点坐标为,抛物线的对称轴是下列结论中:;;方程有两个不相等的实数根;抛物线与x 轴的另一个交点坐标为;若点在该抛物线上,则.其中正确的有A.5个B.4个C.3个D.2个二、填空题(每小题3分,满30分)11.二次函数2(6)8y x =--+的最大值是__________.12.如图,AB 为⊙O 的直径,弦CD⊥AB 于点E ,已知CD =6,EB =1,则⊙O 的半径为_____.13.如图,一下水管道横截面为圆形,直径为100cm ,下雨前水面宽为60cm ,一场大雨过后,水面宽为80cm ,则水位上升_____________ cm .()2y ax bx c a 0=++≠()4,0x 1.=abc 0>①2a b 0+=②③2ax bx c 3++=④()2,0-⑤()A m,n 2am bm c a b c ++≤++()第12小题第13小题14.已知点(﹣1,y1),(﹣321y2,),(﹣2,y3)都在函数y=3(x+1)2﹣2的图象上,则y1,y 2,y3的大小关系为_____________ .15.将抛物线平移,使它的顶点移到点P(-2,3),平移后新抛物线的表达式为____ ____.16.如果抛物线y=ax2﹣2ax+c与x轴的一个交点为(5,0),那么与x轴的另一个交点的坐标是____ ____.17.已知二次函数的图象开口向下,则m的值为____ ___.18.如图,点A是半圆上的三等分点,点B是弧AN的中点,点P是直径MN上一动点,圆O的半径为5cm,则AP+BP的最小值是___ _____ .19.BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD=,则CD的长为________.20.如图,在扇形OAB中,C是OA的中点,,CD与交于点D,以O为圆心,OC的长为半径作交OB于点E,若OA=4,,则图中阴影部分的面积为_______ 结果保留第18小题第20小题三、解答题(满分60分)21.计算(4分x2=8分):(1)3tan30°+4cos60°-2cos45°(2);22.(5分)如图,AB是⊙O的直径,弦CD⊥AB于点E,在圆上取点G,连结CG,DG,AC.求证:∠DGC=2∠BAC.23.(6分)某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.问如何提高售价,才能在半个月内获得最大利润?24.(7分)如图,已知二次函数的图象与x轴交于A( -1,0),B(3,0)两点,与y轴交于点C,顶点D.(1)求这个二次函数的关系式;(2)求四边形ABDC的面积.25.(7分)已知是二次函数,且函数图象有最高点.(1)求k的值;(2)求顶点坐标和对称轴,并说明当x为何值时,y随x的增大而减少.26.(6分)A,B两市相距150千米,分别从A,B处测得国家级风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.27.(7分)小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.(1)求树DE的高度;(2)求食堂MN的高度.28.(14分)如图,抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.(1)直接写出抛物线与x轴的另一个交点B的坐标;(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.若以AB为一底边的梯形ABCD 的面积为9,求此抛物线的解析式,并指出顶点E的坐标;(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.①当t为秒时,△PAD的周长最小?当t为_____________ 秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.。
黑龙江省大庆市2019-2020学年中考第四次质量检测数学试题一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.如图,在△ABC 中,AB=AC=5,BC=8,D 是线段BC 上的动点(不含端点B ,C).若线段AD 长为正整数,则点D 的个数共有( )A .5个B .4个C .3个D .2个2.下列函数中,二次函数是( )A .y =﹣4x+5B .y =x(2x ﹣3)C .y =(x+4)2﹣x 2D .y =21x 3.二次函数y=ax 2+bx+c (a≠0)的图象如图所示,下列说法:①2a+b=0,②当﹣1≤x≤3时,y <0;③3a+c=0;④若(x 1,y 1)(x 2、y 2)在函数图象上,当0<x 1<x 2时,y 1<y 2,其中正确的是( )A .①②④B .①③C .①②③D .①③④4.一次函数y=kx ﹣1的图象经过点P ,且y 的值随x 值的增大而增大,则点P 的坐标可以为( ) A .(﹣5,3) B .(1,﹣3) C .(2,2) D .(5,﹣1)5.某公园有A 、B 、C 、D 四个入口,每个游客都是随机从一个入口进入公园,则甲、乙两位游客恰好从同一个入口进入公园的概率是( )A .12B .14C .16D .186.随着服装市场竞争日益激烈,某品牌服装专卖店一款服装按原售价降价20%,现售价为a 元,则原售价为( )A .(a ﹣20%)元B .(a+20%)元C .a 元D . a 元7.下列图形是轴对称图形的有( )A .2个B .3个C .4个D .5个8.如图,△ABC 中,∠CAB=65°,在同一平面内,将△ABC 绕点A 旋转到△AED 的位置,使得DC ∥AB ,则∠BAE 等于( )A .30°B .40°C .50°D .60°9.下列说法正确的是( )A .﹣3是相反数B .3与﹣3互为相反数C .3与13互为相反数 D .3与﹣13互为相反数 10.如图,△ABC 中,BC =4,⊙P 与△ABC 的边或边的延长线相切.若⊙P 半径为2,△ABC 的面积为5,则△ABC 的周长为( )A .8B .10C .13D .1411.中国幅员辽阔,陆地面积约为960万平方公里,“960万”用科学记数法表示为( )A .0.96×107B .9.6×106C .96×105D .9.6×10212.在同一平面直角坐标系中,函数y=x+k 与k y x=(k 为常数,k≠0)的图象大致是( ) A . B .C .D .二、填空题:(本大题共6个小题,每小题4分,共24分.)13.方程22310x x +-=的两个根为1x 、2x ,则1211+x x 的值等于______. 14.如图,在△ABC 中,AB=AC ,BE 、AD 分别是边AC 、BC 上的高,CD=2,AC=6,那么CE=________.15.已知关于x的方程x2+kx﹣3=0的一个根是x=﹣1,则另一根为_____.16.如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是_________.17.用正三角形、正四边形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个,则第n个图案中正三角形的个数为(用含n 的代数式表示).18.化简代数式(x+1+11x-)÷22xx-,正确的结果为_____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(15,22)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)B点坐标为,并求抛物线的解析式;(2)求线段PC长的最大值;(3)若△PAC为直角三角形,直接写出此时点P的坐标.20.(6分)一个不透明的袋子中装有3个标号分别为1、2、3的完全相同的小球,随机地摸出一个小球不放回,再随机地摸出一个小球.采用树状图或列表法列出两次摸出小球出现的所有可能结果;求摸出的两个小球号码之和等于4的概率.21.(6分)如图,AB 为⊙O 的直径,C 是⊙O 上一点,过点C 的直线交AB 的延长线于点D ,AE ⊥DC ,垂足为E ,F 是AE 与⊙O 的交点,AC 平分∠BAE .求证:DE 是⊙O 的切线;若AE=6,∠D=30°,求图中阴影部分的面积.22.(8分)如图,已知⊙O,请用尺规做⊙O 的内接正四边形ABCD ,(保留作图痕迹,不写做法)23.(8分)如图已知△ABC ,点D 是AB 上一点,连接CD ,请用尺规在边AC 上求作点P ,使得△PBC 的面积与△DBC 的面积相等(保留作图痕迹,不写做法)24.(10分)已知抛物线y =ax 2+(3b+1)x+b ﹣3(a >0),若存在实数m ,使得点P (m ,m )在该抛物线上,我们称点P (m ,m )是这个抛物线上的一个“和谐点”.(1)当a =2,b =1时,求该抛物线的“和谐点”;(2)若对于任意实数b ,抛物线上恒有两个不同的“和谐点”A 、B .①求实数a 的取值范围;②若点A ,B 关于直线y =﹣x ﹣(21a+1)对称,求实数b 的最小值. 25.(10分)如图,已知一次函数12y kx =-的图象与反比例函数()20m y x x =>的图象交于A 点,与x 轴、y 轴交于,C D 两点,过A 作AB 垂直于x 轴于B 点.已知1,2AB BC ==.(1)求一次函数12y kx =-和反比例函数()20m y x x=>的表达式;(2)观察图象:当0x 时,比较12,y y .26.(12分)已知:如图,∠ABC=∠DCB ,BD 、CA 分别是∠ABC 、∠DCB 的平分线.求证:AB=DC .27.(12分)我国沪深股市交易中,如果买、卖一次股票均需付交易金额的0.5%作费用.张先生以每股5元的价格买入“西昌电力”股票1000股,若他期望获利不低于1000元,问他至少要等到该股票涨到每股多少元时才能卖出?(精确到0.01元)参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.C【解析】试题分析:过A 作AE ⊥BC 于E ,∵AB=AC=5,BC=8,∴BE=EC=4,∴AE=3,∵D 是线段BC 上的动点(不含端点B ,C ),∴AE≤AD <AB ,即3≤AD <5,∵AD 为正整数,∴AD=3或AD=4,当AD=4时,E 的左右两边各有一个点D 满足条件,∴点D 的个数共有3个.故选C .考点:等腰三角形的性质;勾股定理.2.B【解析】A. y=-4x+5是一次函数,故此选项错误;B. y= x(2x-3)=2x 2-3x ,是二次函数,故此选项正确;C. y=(x+4)2−x 2=8x+16,为一次函数,故此选项错误;D. y=21x 是组合函数,故此选项错误. 故选B.3.B【解析】∵函数图象的对称轴为:x=-2b a =132-+=1,∴b=﹣2a ,即2a+b=0,①正确; 由图象可知,当﹣1<x <3时,y <0,②错误;由图象可知,当x=1时,y=0,∴a ﹣b+c=0,∵b=﹣2a ,∴3a+c=0,③正确;∵抛物线的对称轴为x=1,开口方向向上,∴若(x 1,y 1)、(x 2,y 2)在函数图象上,当1<x 1<x 2时,y 1<y 2;当x 1<x 2<1时,y 1>y 2;故④错误;故选B .点睛:本题主要考查二次函数的相关知识,解题的关键是:由抛物线的开口方向判断a 与0的关系,由抛物线与y 轴的交点判断c 与0的关系,然后根据对称轴及抛物线与x 轴交点情况进行推理.4.C【解析】【分析】根据函数图象的性质判断系数k >0,则该函数图象经过第一、三象限,由函数图象与y 轴交于负半轴,则该函数图象经过第一、三、四象限,由此得到结论.【详解】∵一次函数y=kx ﹣1的图象的y 的值随x 值的增大而增大,∴k >0,A 、把点(﹣5,3)代入y=kx ﹣1得到:k=﹣45<0,不符合题意; B 、把点(1,﹣3)代入y=kx ﹣1得到:k=﹣2<0,不符合题意;C 、把点(2,2)代入y=kx ﹣1得到:k=32>0,符合题意; D 、把点(5,﹣1)代入y=kx ﹣1得到:k=0,不符合题意,故选C .【点睛】考查了一次函数图象上点的坐标特征,一次函数的性质,根据题意求得k >0是解题的关键.5.B【解析】【分析】画树状图列出所有等可能结果,从中确定出甲、乙两位游客恰好从同一个入口进入公园的结果数,再利用概率公式计算可得.【详解】画树状图如下:由树状图知共有16种等可能结果,其中甲、乙两位游客恰好从同一个入口进入公园的结果有4种,所以甲、乙两位游客恰好从同一个入口进入公园的概率为416=14,故选B.【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A 或B的结果数目m,然后利用概率公式求事件A或B的概率.6.C【解析】【分析】根据题意列出代数式,化简即可得到结果.【详解】根据题意得:a÷(1−20%)=a÷= a(元),故答案选:C.【点睛】本题考查的知识点是列代数式,解题的关键是熟练的掌握列代数式.7.C【解析】试题分析:根据轴对称图形的概念:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.据此对图中的图形进行判断.解:图(1)有一条对称轴,是轴对称图形,符合题意;图(2)不是轴对称图形,因为找不到任何这样的一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意;图(3)有二条对称轴,是轴对称图形,符合题意;图(3)有五条对称轴,是轴对称图形,符合题意;图(3)有一条对称轴,是轴对称图形,符合题意.故轴对称图形有4个.故选C.考点:轴对称图形.8.C【解析】试题分析:∵DC∥AB,∴∠DCA=∠CAB=65°.∵△ABC绕点A旋转到△AED的位置,∴∠BAE=∠CAD,AC=AD.∴∠ADC=∠DCA="65°." ∴∠CAD=180°﹣∠ADC﹣∠DCA="50°." ∴∠BAE=50°.故选C.考点:1.面动旋转问题;2. 平行线的性质;3.旋转的性质;4.等腰三角形的性质.9.B【解析】【分析】符号不同,绝对值相等的两个数互为相反数,可据此来判断各选项是否正确.【详解】A、3和-3互为相反数,错误;B、3与-3互为相反数,正确;C、3与13互为倒数,错误;D、3与-13互为负倒数,错误;故选B.【点睛】此题考查相反数问题,正确理解相反数的定义是解答此题的关键.10.C【解析】【分析】根据三角形的面积公式以及切线长定理即可求出答案.【详解】连接PE、PF、PG,AP,由题意可知:∠PEC=∠PFA=PGA=90°,∴S△PBC=12BC•PE=12×4×2=4,∴由切线长定理可知:S△PFC+S△PBG=S△PBC=4,∴S四边形AFPG=S△ABC+S△PFC+S△PBG+S△PBC=5+4+4=13,∴由切线长定理可知:S△APG=12S四边形AFPG=132,∴132=12×AG•PG,∴AG=132,由切线长定理可知:CE=CF,BE=BG,∴△ABC的周长为AC+AB+CE+BE=AC+AB+CF+BG=AF+AG=2AG=13,故选C.【点睛】本题考查切线长定理,解题的关键是画出辅助线,熟练运用切线长定理,本题属于中等题型.11.B【解析】试题分析:“960万”用科学记数法表示为9.6×106,故选B.考点:科学记数法—表示较大的数.12.B【解析】【分析】【详解】选项A中,由一次函数y=x+k的图象知k<0,由反比例函数y=的图象知k>0,矛盾,所以选项A错误;选项B中,由一次函数y=x+k的图象知k>0,由反比例函数y=的图象知k>0,正确,所以选项B正确;由一次函数y=x+k的图象知,函数图象从左到右上升,所以选项C、D错误.故选B.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.1.【解析】【分析】根据一元二次方程根与系数的关系求解即可.【详解】 解:根据题意得1232x x +=-,1212x x =-, 所以1211+x x =1212x x x x +=3212--=1. 故答案为1.【点睛】本题考查了根与系数的关系:若1x 、2x 是一元二次方程20ax bx c ++=(a≠0)的两根时,12b x x a +=-,12c x x a =. 14.43【解析】∵AB=AC ,AD ⊥BC ,∴BD=CD=2,∵BE 、AD 分别是边AC 、BC 上的高, ∴∠ADC=∠BEC=90°,∵∠C=∠C ,∴△ACD ∽△BCE , ∴AC CD BC CE=, ∴624CE=, ∴CE=43, 故答案为43. 15.1【解析】【分析】设另一根为x 2,根据一元二次方程根与系数的关系得出-1•x 2=-1,即可求出答案.【详解】设方程的另一个根为x 2,则-1×x 2=-1, 解得:x 2=1,故答案为1.【点睛】本题考查了一元二次方程根与系数的关系:如果x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么x1+x2=-ba,x1x2=ca.16.1【解析】【分析】画出图形,设菱形的边长为x,根据勾股定理求出周长即可.【详解】当两张纸条如图所示放置时,菱形周长最大,设这时菱形的边长为xcm,在Rt△ABC中,由勾股定理:x2=(8-x)2+22,解得:x=17 4,∴4x=1,即菱形的最大周长为1cm.故答案是:1.【点睛】解答关键是怎样放置纸条使得到的菱形的周长最大,然后根据图形列方程.17.4n+1【解析】【分析】分析可知规律是每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个.【详解】解:第一个图案正三角形个数为6=1+4;第二个图案正三角形个数为1+4+4=1+1×4;第三个图案正三角形个数为1+1×4+4=1+3×4;…;第n个图案正三角形个数为1+(n﹣1)×4+4=1+4n=4n+1.故答案为4n+1.考点:规律型:图形的变化类.18.2x【解析】【分析】根据分式的运算法则计算即可求解. 【详解】(x+1+11x-)÷22xx-=()()() 1111121 x x xx x x⎡⎤+-+÷⎢⎥---⎣⎦=() 2211xxx x-⋅-=2x.故答案为2x.【点睛】本题考查了分式的混合运算,熟知分式的混合运算顺序及运算法则是解答本题的关键.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(1)(4,6);y=1x1﹣8x+6(1)498;(3)点P的坐标为(3,5)或(711,22).【解析】【分析】(1)已知B(4,m)在直线y=x+1上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(1)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)根据顶点问题分情况讨论,若点P为直角顶点,此图形不存在,若点A为直角顶点,根据已知解析式与点坐标,可求出未知解析式,再联立抛物线的解析式,可求得C点的坐标;若点C为直角顶点,可根据点的对称性求出结论.【详解】解:(1)∵B(4,m)在直线y=x+1上,∴m=4+1=6,∴B(4,6),故答案为(4,6);∵A(,),B(4,6)在抛物线y=ax1+bx+6上,∴,解得,∴抛物线的解析式为y=1x1﹣8x+6;(1)设动点P的坐标为(n,n+1),则C点的坐标为(n,1n1﹣8n+6),∴PC=(n+1)﹣(1n1﹣8n+6),=﹣1n1+9n﹣4,=﹣1(n﹣)1+,∵PC>0,∴当n=时,线段PC最大且为.(3)∵△PAC为直角三角形,i)若点P为直角顶点,则∠APC=90°.由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;ii)若点A为直角顶点,则∠PAC=90°.如图1,过点A(,)作AN⊥x轴于点N,则ON=,AN=.过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0).设直线AM的解析式为:y=kx+b,则:,解得,∴直线AM的解析式为:y=﹣x+3 ①又抛物线的解析式为:y=1x1﹣8x+6 ②联立①②式,解得:或(与点A重合,舍去),∴C(3,0),即点C、M点重合.当x=3时,y=x+1=5,∴P1(3,5);iii)若点C为直角顶点,则∠ACP=90°.∵y=1x1﹣8x+6=1(x﹣1)1﹣1,∴抛物线的对称轴为直线x=1.如图1,作点A(,)关于对称轴x=1的对称点C,则点C在抛物线上,且C(,).当x=时,y=x+1=.∴P1(,).∵点P1(3,5)、P1(,)均在线段AB上,∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(,).【点睛】本题考查了二次函数的综合题,解题的关键是熟练的掌握二次函数的应用.20.(1)见解析;(2)1 3 .【解析】【分析】(1)画树状图列举出所有情况;(2)让摸出的两个球号码之和等于4的情况数除以总情况数即为所求的概率.【详解】解:(1)根据题意,可以画出如下的树形图:从树形图可以看出,两次摸球出现的所有可能结果共有6种.(2)由树状图知摸出的两个小球号码之和等于4的有2种结果,∴摸出的两个小球号码之和等于4的概率为=.【点睛】本题要查列表法与树状图法求概率,列出树状图得出所有等可能结果是解题关键.21.(1)证明见解析;(2)阴影部分的面积为8833π-.【解析】【分析】(1)连接OC,先证明∠OAC=∠OCA,进而得到OC∥AE,于是得到OC⊥CD,进而证明DE是⊙O 的切线;(2)分别求出△OCD的面积和扇形OBC的面积,利用S阴影=S△COD﹣S扇形OBC即可得到答案.【详解】解:(1)连接OC,∵OA=OC,∴∠OAC=∠OCA,∵AC平分∠BAE,∴∠OAC=∠CAE,∴∠OCA=∠CAE,∴OC∥AE,∴∠OCD=∠E,∵AE⊥DE,∴∠E=90°,∴∠OCD=90°,∴OC⊥CD,∵点C在圆O上,OC为圆O的半径,∴CD是圆O的切线;(2)在Rt△AED中,∵∠D=30°,AE=6,∴AD=2AE=12,在Rt△OCD中,∵∠D=30°,∴DO=2OC=DB+OB=DB+OC,∴DB=OB=OC=AD=4,DO=8,∴CD=22228443-=-=DO OC∴S△OCD=43422⋅⨯=CD OC=83,∵∠D=30°,∠OCD=90°,∴∠DOC=60°,∴S扇形OBC=16×π×OC2=83π,∵S阴影=S△COD﹣S扇形OBC ∴S阴影=83﹣83π,∴阴影部分的面积为83﹣83π.22.见解析【解析】【分析】根据内接正四边形的作图方法画出图,保留作图痕迹即可.【详解】任作一条直径,再作该直径的中垂线,顺次连接圆上的四点即可.【点睛】此题重点考察学生对圆内接正四边形作图的应用,掌握圆内接正四边形的作图方法是解题的关键. 23.见解析【解析】【分析】三角形的面积相等即同底等高,所以以BC为两个三角形的公共底边,在AC边上寻找到与D到BC距离相等的点即可.【详解】作∠CDP=∠BCD,PD与AC的交点即P.【点睛】本题考查了三角形面积的灵活计算,还可以利用三角形的全等来进行解题.24.(1)(11,22)或(﹣1,﹣1);(1)①2<a<17②b的最小值是13【解析】【分析】(1)把x=y=m,a=1,b=1代入函数解析式,列出方程,通过解方程求得m的值即可;(1)抛物线上恒有两个不同的“和谐点”A、B.则关于m的方程m=am1+(3b+1)m+b-3的根的判别式△=9b1-4ab+11a.①令y=9b 1-4ab+11a ,对于任意实数b ,均有y >2,所以根据二次函数y=9b 1-4ab+11的图象性质解答; ②利用二次函数图象的对称性质解答即可.【详解】(1)当a =1,b =1时,m =1m 1+4m+1﹣4,解得m =12或m =﹣1. 所以点P 的坐标是(12,12)或(﹣1,﹣1); (1)m =am 1+(3b+1)m+b ﹣3,△=9b 1﹣4ab+11a .①令y =9b 1﹣4ab+11a ,对于任意实数b ,均有y >2,也就是说抛物线y =9b 1﹣4ab+11的图象都在b 轴(横轴)上方.∴△=(﹣4a )1﹣4×9×11a <2.∴2<a <17.②由“和谐点”定义可设A (x 1,y 1),B (x 1,y 1),则x 1,x 1是ax 1+(3b+1)x+b ﹣3=2的两不等实根,123122x x b a ++=-. ∴线段AB 的中点坐标是:(﹣312b a +,﹣312b a +).代入对称轴y =x ﹣(21a +1),得 ﹣312b a +=312b a +﹣(21a+1), ∴3b+1=1a+a . ∵a >2,1a >2,a•1a =1为定值,∴3b+1=1a =1, ∴b≥13. ∴b 的最小值是13. 【点睛】此题考查了二次函数综合题,其中涉及到了二次函数图象上点的坐标特征,抛物线与x 轴的交点,一元二次方程与二次函数解析式间的关系,二次函数图象的性质等知识点,难度较大,解题时,掌握“和谐点”的定义是解题的难点.25.(1)()12162,02y x y x x=-=>;(2)12121206,;6,;6,x y y x y y x y y <== 【解析】【分析】(1)由一次函数的解析式可得出D 点坐标,从而得出OD 长度,再由△ODC 与△BAC 相似及AB 与BC 的长度得出C 、B 、A 的坐标,进而算出一次函数与反比例函数的解析式;(2)以A 点为分界点,直接观察函数图象的高低即可知道答案.【详解】解:(1)对于一次函数y=kx-2,令x=0,则y=-2,即D (0,-2),∴OD=2,∵AB ⊥x 轴于B , ∴AB OD BC OC= , ∵AB=1,BC=2,∴OC=4,OB=6,∴C (4,0),A (6,1)将C 点坐标代入y=kx-2得4k-2=0,∴k=12, ∴一次函数解析式为y=12x-2; 将A 点坐标代入反比例函数解析式得m=6, ∴反比例函数解析式为y=6x ; (2)由函数图象可知:当0<x <6时,y 1<y 2;当x=6时,y 1=y 2;当x >6时,y 1>y 2;【点睛】本题考查了反比例函数与一次函数的交点问题.熟悉函数图象上点的坐标特征和待定系数法解函数解析式的方法是解答本题的关键,同时注意对数形结合思想的认识和掌握.26.∵AC 平分BCD BC ∠,平分ABC ∠,∴ACB DBC ∠=∠在ABC V 与DCB V 中,{ABC DCBACB DBC BC BC∠=∠∠=∠=ABC ∴V DCB V ≌AB DC ∴=.【解析】分析:根据角平分线性质和已知求出∠ACB=∠DBC ,根据ASA 推出△ABC ≌△DCB ,根据全等三角形的性质推出即可.解答:证明:∵AC 平分∠BCD ,BC 平分∠ABC ,∴∠DBC=12∠ABC ,∠ACB=12∠DCB , ∵∠ABC=∠DCB ,∴∠ACB=∠DBC ,∵在△ABC 与△DCB 中,ABC DCB{BC BC ACB DBC∠=∠=∠=∠,∴△ABC ≌△DCB ,∴AB=DC .27.至少涨到每股6.1元时才能卖出.【解析】【分析】根据关系式:总售价-两次交易费≥总成本+1000列出不等式求解即可.【详解】解:设涨到每股x 元时卖出,根据题意得1000x-(5000+1000x )×0.5%≥5000+1000,解这个不等式得x≥1205199, 即x≥6.1.答:至少涨到每股6.1元时才能卖出.【点睛】本题考查的是一元一次不等式在生活中的实际运用,解决本题的关键是读懂题意根据“总售价-两次交易费≥总成本+1000”列出不等关系式.。
2019---2020学年度上学期期中初三物理试题考生注意:1、考试时间75分钟2选项中,只有一项是符合题目要求的,请将正确选项的序号填涂在答题卡上)1.(4分)在探索之路上,有众多的科学家披荆斩棘,铺路架桥,为后人留下了果实丰硕的知识园地,下列科学家与其贡献不相符的是()A.哥白尼日心说B.牛顿量子力学C.爱因斯坦相对论D.伽利略率先用望远镜观察天空2.(4分)学习物理能让我们更好地了解生活中的一些数据,以下说法与事实相符的是()A.一本初中物理教材的质量约是5kg B.正常情况下,人的脉搏跳动约为1次/s C.课桌的高度大约是100dm D.人散步的速度约为10m/s3.(4分)下列说法不正确的是()A.在建筑方面,设计、建造大礼堂时,必须把回声现象作为重要因素加以考虑B.动画片的配音常用慢录快放的方式,把成年人的声音变成了小孩的声音,这样能够使声音音调变高C.超声波能将一般情况下不能混合的液体混合在一起,而次声波人耳听不到,能量很小,破坏力不大D.广播里播放“考生开始答题”的声音是通过空气传入同学们耳朵的4.(4分)下列说法中正确的是()A.声音在真空中可以传播B.物体到平面镜的距离决定了物体在平面镜中成像的大小C.蜡烛放在凸透镜的2倍焦距处,移动光屏可以得到等大、倒立的虚像D.在石油勘探时常采用人工地震,利用探头接收地下不同层间界面反射回来的声波,从而探测出地下油矿5.(4分)如图是某物体在水平地面上作直线运动的s-t图像,以下结论正确的是()A.物体在0-2S内做变速运动B.物体在2-4S内运动速度是5m/sC.物体在前2S内和后2S的速度相等D. 物体在6S内运动平均速度是2.5m/s6.(4分)明代诗人曾写下这样的诗句:“空手把锄头,步行骑水牛。
人在桥上走,桥流水不流。
”其中“桥流水不流”,诗人选择的参照物()A.桥 B.河岸C.水D.岸上的树7.(4分).观赏水面风景照片时,总发现景物的“倒影”比本身暗一些,这是由于 ( )A .“倒影”比真实景物的清晰度差B .入射水面的光线有一部分折射入水中C .光线被反射掉一部分D .冲洗照片质量有问题8.(4分).成语“白纸黑字”喻指证据确凿,不容抵赖。
2019——2020学年度第一学期期中测试题初二数学试题一.选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项写在括号内)。
1.下列计算正确的是( )A .a 3•a 2=a 6B .a 3﹣a 2=aC .(﹣a )2•(﹣a )=﹣a 3D .a 6÷a 2=a 32.一种新型病毒直径约为0.000043毫米,用科学记数法表示为( )毫米. A .0.43×10﹣4B .0.43×10﹣5C .4.3×10﹣5D .4.3×10﹣83.在下列计算中,不能用平方差公式计算的是( )A .(m ﹣n )(﹣m+n ) B .(x 3﹣y 3)(x 3+y 3) C .(﹣a ﹣b )(a ﹣b )D .(c 2﹣d 2)(d 2+c 2)4.如果一个角的两边分别平行于另一个角两边,那么这两个角( ) A.相等 B.互补 C.相等或互补 D.以上结论都不对5.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q (升)与行驶时间t (时)的关系用图象表示应为图中的( )6.下列正确说法的个数是( )①同位角相等;②等角的补角相等;③两直线平行,同旁内角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直. A.1B.2C.3D.47.如图,给出下列条件,其中能推出AB ∥DC 的是( )(1)∠1=∠2(2)∠3=∠4(3)∠B=∠DCE(4)AD ∥BC 且∠B=∠DA.(1)(4)B.(2)(3)C.(1)(3)D.(1)(3)(4) 8.如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上. 如果∠1=20°,那么∠2的度数是( ) A.15°B.20°C.25°D.30°第7题图 第8题图9. 若a +b =5,ab =﹣24,则a 2+b 2的值等于( )A .73B .49C .43D .2310.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm )与所挂重物的质量x (kg )有下面的关系,那么弹簧总长y (cm )与所挂重物x (kg )之间的关系式为( )A.y=0.5x+12B.y=x+10.5C.y=0.5x+10D.y=x+12二、填空题:(每小题3分,共24分. )11.计算()=⨯-20082007425.0_______。
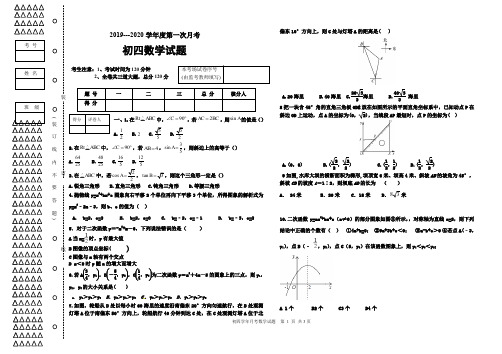
2019—2020学年度第一学期期中质量检测
初 四 (数学)试题
一、选择题:(每小题3分,共计30分) 1.抛物线y=2(x+3)2
+5的顶点坐标是( ) A .(3,5) B .(﹣3,5) C .(3,﹣5) D .(﹣3,﹣5) 2.如图,
点A 、B 、C 都在圆O 上,若∠AOB =72°,则∠ACB 的度数为( ) A. 18° B. 30° C. 36°
D. 72°
3.已知⊙A 半径为5,圆心A 的坐标为(
1,0)
,点P 的坐标为(﹣2,4), 则点P 与⊙A 的位置关系是( ) A. 点P 在⊙A 上B. 点P 在⊙A 内 C. 点P 在⊙A 外D. 不能确定 4.在△ABC 中,∠C=90°,如果tanA= ,那么sinB 的值等于( ) A. B. C. D.
第2小题 第5小题
5.如图,四边形ABCD 是⊙O 的内接四边形,若∠B=75°,∠C=85°, 则∠D﹣∠A 的度数差为( )
A. 10°
B. 15°
C. 20°
D. 25°
6.已知抛物线y =(a +1)x 2-ax -8,过点(2,-2),且与x 轴的一个交点的横坐标为2n ,则代数式4n 2-n +2016 的值为( ) A.2020
B.2019
C.2018
D.2017
7.抛物线y=x 2﹣2x+1与坐标轴交点个数为( ) A. 无交点 B. 1个 C. 2个
D. 3个 8.在直角三角形中两个锐角的正弦值的平方和为( )
A. 0.5
B. 1
C. 2
D. 2.5 9.如图,将Rt△ABC 形状的楔子从木桩的底端P 沿水平方向打入木桩,使木桩向上运动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6cm (如箭头所示),则木桩上升了( ) A. 6sin15°cm B. 6cos15°cm C. 6tan15° cm D. cm
第9小题 第10小题
10.抛物线()2
y ax bx c a 0=++≠的部分图象如图所示,与x 轴的一个交点坐标为()4,0,抛物线的对称轴是x 1.=下列结论中:
abc 0>①;2a b 0
+=②;③
方程2
ax bx c 3++
=有两个不相等的实数根;④
抛物线与
x
轴的另一个交点坐标为()2,0-;⑤
若点()
A m,n
在该抛物线上,则2am bm c a
b c ++
≤
++.其中正确的有(
) A.5个
B.4个
C.3个
D.2个
班 级
姓
名
( 装
订
线
内 不
要
答
题 )
二、填空题(每小题3分,满30分)
11.二次函数2(6)8y x =--+的最大值是__________.
12.如图,AB 为⊙O 的直径,弦CD⊥AB 于点E ,已知CD =6,EB =1,则⊙O 的半径为_____.
13.如图,一下水管道横截面为圆形,直径为100cm ,下雨前水面宽为60cm ,一场大雨过后,水面宽为80cm ,则水位上升_____________ cm .
第12小题 第13小题
14.已知点(﹣1,y 1),(﹣321
y 2
,),(﹣2,y 3)都在函数y=3(x+1)2﹣2
的图象上,则y 1,y 2,y 3的大小关系为_____________ . 15.将抛物线
平移,使它的顶点移到点P (-2,3),平移后新抛物线
的表达式为____ ____.
16.如果抛物线y=ax 2﹣2ax+c 与x 轴的一个交点为(5,0),那么与x 轴的另一个交点的坐标是____ ____. 17.已知二次函数
的图象开口向下,则m 的值为____ ___.
18.如图,点A 是半圆上的三等分点,点B 是弧AN 的中点,点P 是直径MN 上一动点,圆O 的半径为5cm,则AP+BP 的最小值是___ _____ . 19.BD 为等腰△ABC 的腰AC 上的高,BD =1,tan∠ABD=
,则CD 的长为
________.
20.如图,在扇形OAB 中,C 是OA 的中点, ,CD 与
交于点D ,
以O 为圆心,OC 的长为半径作
交OB 于点E ,若OA=4,
,则
图中阴影部分的面积为____ ___ 结果保留
第18小题 第20小题 三、解答题(满分60分) 21.计算(4分x2=8分):
(1)3tan30°+4cos60°-2cos45° (2) ;
22.(5分)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,在圆上取点G ,连结
CG ,DG ,AC .
求证:∠DGC =2∠BAC .
23.(6分)某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.问如何提高售价,才能在半个月内获得最大利润?
24.(7分)如图,已知二次函数的图象与x轴交于A( -1,0),B(3,0)两点,与y轴交于点C,顶点D.
(1)求这个二次函数的关系式;
(2)求四边形ABDC的面积. 25.(7分)已知
是二次函数,且函数图象有最高点.(1)求k的值;
(2)求顶点坐标和对称轴,并说明当x为何值时,y随x的增大而减少.
26.(6分)A,B两市相距150千米,分别从A,B处测得国家级风景区中心C 处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆,
tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.
27.(7分)小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.(1)求树DE的高度;(2)求食堂MN的高度.28.(14分)如图,抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.
(1)直接写出抛物线与x轴的另一个交点B的坐标;
(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.若以AB为一底边的梯形ABCD 的面积为9,求此抛物线的解析式,并指出顶点E的坐标;(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.
①当t为秒时,△PAD的周长最小?当t为_____________ 秒时,△PAD 是以AD为腰的等腰三角形?(结果保留根号)
②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.。