创意平板折叠桌的数学模型数学建模B题92620850

创意平板折叠桌摘要本文针对给出创意平板折叠桌的桌子高度和桌面直径，为得出最优设计加工参数以及最优选材等问题建立数学模型并求解。

针对问题一，定义圆的弦长方向与木板的长度方向平行，利用弦长公式计算出除最外围木条其余圆周内木条的长度，将所求的木条长度导入到Matlab软件中使用cubic方式拟合曲线，求出最外围木条的长度。

为描述动态变化过程，引用等效替代的思想，建立模型，用桌腿与桌子高度间的夹角变换客观明确的表现出折叠过程中的动态变化。

根据以上数据求出折叠桌的设计加工参数以及桌脚边缘线。

针对问题二，在不影响到外形美观度的基础上，先以用材最少为目标函数，用稳定性好和加工方便为约束条件，建立优化模型，使用Lingo软件编程求出部分参数最优解，根据求出的最优解系统计算汇总得出所求创意平板折叠桌的最优设计加工参数。

针对问题三，此问是要建立设计加工参数的通解，需要考虑不同的桌面形状，建立不同的模型，在输入数据时先判断属于哪个桌面形状，任意给出折叠桌高度、桌面边缘线的形状大小和桌脚边缘线的大致形状，利用建立的模型求解其设计加工参数，绘制动态变化过程示意图。

关键词：创意平板折叠桌；拟合；最优化模型；空间几何一、问题重述创意平板折叠桌在外型新颖、造型美观的基础上，还要全面考虑折叠桌制作的稳固性、加工时长以及用材量。

在已知桌高和桌面直径的条件下，建立数学模型，快速且精确的算出最优的设计加工参数。

就已知折叠桌桌高以及桌面直径的情况下，建立数学模型分析研究下面的问题：（1）根据所给的已知条件，建立数学模型，来描述此折叠桌的动态变化过程，在此基础上给出此折叠桌的设计加工参数和桌脚边缘线的数学描述。

（2）在造型美观的前提下，考虑稳固性，加工方便，用材等影响因素，在已知桌高和桌面直径的情况下，建立数学模型，确定最优设计加工方案。

（3）根据任意设定的折叠桌高度、桌面边缘线的形状大小和桌脚边缘线的大致形状，给出所需平板材料的形状尺寸和切实可行的最优设计加工参数，使得生产的折叠桌尽可能接近所期望的形状。

B 题 创意平板折叠桌摘 要本文针对折叠桌的特点，将其抽象成简单的数学模型，按题目中的要求，应用立体几何图形和运筹学的方法建立数学模型并求解.对问题一，依据题目中的数据应用Ｍatlab 和Soli ｄW ｏrks 软件，对折叠桌的运动过程进行动态模拟和分析,然后将该折叠桌抽象成立体几何图形建立模型,应用几何图解法和向量法，对折叠桌的桌腿长和桌腿木条开槽的长度进行求解得到开槽长度为：对问题二，折叠桌放置在地面，不考虑木条的形变时，只有四个边缘桌腿受力,钢筋对各个桌腿的力为零.假设折叠桌与木地面有一定的摩擦力，对桌腿进行受力分析,桌腿只在两个端点处受力,是二力杆，根据木头间的摩擦因数即可得到桌腿发生自锁时桌腿与竖直方向的最大角度21.8。

给折叠桌一个稳定安全因数 1.2s n =，便可得到折叠桌的安全角度=18.44α.根据α大小，桌面高度和圆形桌面直径，可以得到各个桌腿长度。

加工程度考虑木条槽长的总长，因此得到优化目标为加工的木条槽长最短,当桌高7０ ｃm,桌面直径80 cm 时，解得木板长a =16７.４16ｃm 钢筋距边缘桌腿末端的距离为()11=31.1322aL x -+cm 针对问题三，我们在问题一的基础上将其模型进行一般化处理，从桌面边缘线的形状，大小出发,给出软件设计的模型。

在该模型设计的基础上，我们根据自己设定的参数，相应地应用Sol ｉdWorks 设计新型的平板折叠桌,其中有菱形桌面和椭圆型桌面,见图6~图１２。

关键字:立体几何图形 动态模拟 自锁 Sol ｉdW ｏrks一、问题的重述某公司生产一种可折叠的桌子，桌面呈圆形，桌腿随着铰链的活动可以平摊成一张平板（如图1－2所示）。

桌腿由若干根木条组成，分成两组，每组各用一根钢筋将木条连接，钢筋两端分别固定在桌腿各组最外侧的两根木条上,并且沿木条有空槽以保证滑动的自由度(见图3)。

桌子外形由直纹曲面构成，造型美观。

附件视频展示了折叠桌的动态变化过程。

对创意平板折叠桌的最优化设计摘要本文主要研究了创意平板折叠桌的相关问题。

对于问题一，首先，我们根据所提供的已知尺寸的长方形平板和桌面形状，桌高的要求，以圆桌面中心作为原点建立了相应的空间直角坐标系，分别求出了各个桌腿的长度，根据在折叠过程中，钢筋穿过的每个点距离桌面的高度相同这一性质，利用MATLAB程序计算出了每根木棒卡槽的长度和桌脚底端每个点的坐标，其中卡槽长度依次为（从最外侧开始，单位：cm）：0、 4.3564、7.663、10.3684、12.5926、14.393、15.8031、16.8445、17.5314、17.8728，并且根据底端坐标拟合出了桌脚边缘线的方程并进行了检验。

另外，我们通过桌脚边缘线的变化图像来描述折叠桌的折叠过程。

对于问题二，我们以用材最少为目标函数，以稳固性好为约束条件，通过对桌腿进行力学分析和几何分析得到了使得用材最少且稳固性好的圆桌需要满足的条件是钢筋穿过最长腿的位置满足一个不等式。

并且，当平板的长为163.4702cm,宽为80cm,厚度为3cm,最外侧桌腿钢筋处到桌腿底端的距离与桌腿的长度之比为0.4186时，木板的用材最小，其对应的体积V为392330cm3。

对于问题三，为了满足客户需求，使得生产的折叠桌尽可能接近客户所期望的形状，我们给出了软件设计的基本算法。

我们考虑了“操场形”桌面和“双曲线形”桌面，得到了“操场形”桌面的的创意平板折叠桌槽长为（从最外侧开始，单位：cm）：0、4.3564、7.6637、10.3684、12.5926、14.3930、15.8031、16.8445、17.5314、17.8728; “曲线形”桌面的创意平板折叠桌槽长为（从最外侧开始，单位：cm）：0、1.5756、2.8917、3.9886、4.9005、5.6532、6.2641、6.7397、7.0741、7.2501。

最后，给出了两种桌面的动态变化图。

关键字：曲线拟合最优化设计几何模型折叠桌桌脚边缘线一、问题重述问题背景某公司生产一种可折叠的桌子，桌面呈圆形，桌腿随着铰链的活动可以平摊成一张平板。

折叠桌的设计应做到产品稳固性好（力学性能分析）、加工方便、用材最少。

对于任意给定的折叠桌高度和圆形桌面直径的设计要求，讨论长方形平板材料和折叠桌的最优设计加工参数，例如，平板尺寸、钢筋位置、开槽长度等(再加一个特色的)。

对于桌高70 cm，桌面直径80 cm的情形，确定最优设计加工参数。

假设桌面均匀受力。

根据题意，为了提高稳固性，需要做力学性能研究，一个好的设计没有实用性就不能使用，所以我们把力学性能分析放在首要地位。

为了使加工更加方便和用材最少，我们会在稳固性好的前提下减少使用的钢筋数量和选择最优加工参数。

首先对于设计者设计的桌子的力学性能分析。

我们将作品除支撑外的所有木条以及对应的销钉和绞都去掉，得到如下图所示的结构（图中另一侧的两个台脚没有画出，实际存在）。

其对应的两种力学模型如图所示：左图是对应简支梁的弯矩图，若f即摩擦力不足够大，则会导致结构发生变化。

右图则是对应桌脚铰接于地面的图，该结构处于几何可变状态，不能受力。

因此我们选择左图对应的力学模型来分析此问题。

当结构增加了木条连接销钉和桌面，形成如下图所示的结构：根据力学原理，每增加一根木条，该结构的超静定次数便多增加一次，因此该结构为多次超静定结构，采取增加木条的方法来增加超静定次数, 降低受力敏感度，是提高其稳定性的重要因素。

多年的工程实践证明, 采用优良的结构形式, 对抵抗较大幅度的超载、随机外力以及避免脆性破坏或连续破坏有十分重要的意义。

另外，为了尽可能减少摩擦力对整个结构受力的影响，桌脚木条与水平面的夹角应该有所限制。

若杆AB的长度为L, f为摩擦力，N为支持力。

根据力矩平衡，对B点求矩，ΣM B=N∙L∙cosθ−f∙L∙sinθ=0，求得f=N∙cotθ，因此θ角趋向于90°时，也即桌脚与水平面垂直的时候，摩擦力为0，此时摩擦力对桌子结构的影响最小。

但是当考虑整体结构的时候，若桌脚与水平面垂直的时候，其他木条则均处于桌面下侧，并向里侧收缩如图所示：根据受力平衡，对于桌脚木条来说就会受到销钉提供的很大的向外侧的力作用，对于力学性能来说是一个很大的影响，因此对于整体结构来说，桌脚与水平面的夹角为90°并不是最佳角度。

第三小问： 公司计划开发一种折叠桌设计软件，根据客户任意设定的折叠桌高度、桌面边缘线的形状大小和桌脚边缘线的大致形状，给出所需平板材料的形状尺寸和切实可行的最优设计加工参数，使得生产的折叠桌尽可能接近客户所期望的形状。

你们团队的任务是帮助给出这一软件设计的数学模型，并根据所建立的模型给出几个你们自己设计的创意平板折叠桌。

要求给出相应的设计加工参数，画出至少8张动态变化过程的示意图。

针对第三小问我们的解题思路是：首先我们考虑如何刻画桌面边缘线的形状大小，当用户给定桌面边缘线的期望形状时，在桌子放平二维平面上，我们可以通过对边缘线上每一点i 距离桌面中心线的距离i m 的计算，来近似描述用户需要的左面边缘线的轮廓。

我们通过用户给定的折叠桌的高度H ，和桌面边缘线的形状大小来来找到一组平板材料的形状尺寸和切实可行的加工参数，去尽量满足用户需要的桌角边缘线的大致形状。

首先我们遵循第二小问中的三条约束条件，钢筋位置约束1r a l<<，开槽长度约束max00x s l r =<<-，还有桌子高度约束()max x r H z l =±≤≤。

其次，关于对称性的约束，为了满足折叠桌能顺利展开和稳定摆放，我们必须考虑其对称性，即要求客户对桌面边缘的要求必须是关于桌子的中线是对称的，且还需要是左右对称的。

为了尽量满足用户对桌角边缘线的要求，我们设计了第四个目标条件：2241min ((a,)y )((a,))n i i i i i T y l z l z =⎧⎫⎡⎤=-+-⎨⎬⎣⎦⎩⎭∑ 其中y i 和i z 代表了，其表示了在桌子立起来时的稳定状态下，用户需要的桌角边缘线中每一点i 的y 和z 坐标值，(a,)i y l 和(a,)i z l 分别代表了我们进行优化选择的平板尺寸和加工参数之后的桌子立起来的稳定状态下的桌角边缘线的每一点i 的y 和z 坐标值。

当4T 越趋近于0时，我们可以说此时选取的平板尺寸和加工参数加工出来的桌子，在立起来稳定的时候所产生的桌角边缘线可以更好地满足客户对桌角边缘线的要求。

数学建模2010-2015试题2015年A: 太阳影⼦定位如何确定视频的拍摄地点和拍摄⽇期是视频数据分析的重要⽅⾯，太阳影⼦定位技术就是通过分析视频中物体的太阳影⼦变化，确定视频拍摄的地点和⽇期的⼀种⽅法。

1.建⽴影⼦长度变化的数学模型，分析影⼦长度关于各个参数的变化规律，并应⽤你们建⽴的模型画出2015年10⽉22⽇北京时间9:00-15:00之间天安门⼴场（北纬39度54分26秒,东经116度23分29秒）3⽶⾼的直杆的太阳影⼦长度的变化曲线。

2.根据某固定直杆在⽔平地⾯上的太阳影⼦顶点坐标数据，建⽴数学模型确定直杆所处的地点。

将你们的模型应⽤于附件1的影⼦顶点坐标数据，给出若⼲个可能的地点。

3. 根据某固定直杆在⽔平地⾯上的太阳影⼦顶点坐标数据，建⽴数学模型确定直杆所处的地点和⽇期。

将你们的模型分别应⽤于附件2和附件3的影⼦顶点坐标数据，给出若⼲个可能的地点与⽇期。

4．附件4为⼀根直杆在太阳下的影⼦变化的视频，并且已通过某种⽅式估计出直杆的⾼度为2⽶。

请建⽴确定视频拍摄地点的数学模型，并应⽤你们的模型给出若⼲个可能的拍摄地点。

如果拍摄⽇期未知，你能否根据视频确定出拍摄地点与⽇期？B：“互联⽹+”时代的出租车资源配置出租车是市民出⾏的重要交通⼯具之⼀，“打车难”是⼈们关注的⼀个社会热点问题。

随着“互联⽹+”时代的到来，有多家公司依托移动互联⽹建⽴了打车软件服务平台，实现了乘客与出租车司机之间的信息互通，同时推出了多种出租车的补贴⽅案。

请你们搜集相关数据，建⽴数学模型研究如下问题：(1) 试建⽴合理的指标，并分析不同时空出租车资源的“供求匹配”程度。

(2) 分析各公司的出租车补贴⽅案是否对“缓解打车难”有帮助？(3) 如果要创建⼀个新的打车软件服务平台，你们将设计什么样的补贴⽅案，并论证其合理性。

2014年A:嫦娥三号软着陆轨道设计与控制策略嫦娥三号于2013年12⽉2⽇1时30分成功发射，12⽉6⽇抵达⽉球轨道。

作者： 郑路通 郭志鹏 牛星月 李亚琴 孙国伟
作者机构： 运城学院应用数学系,山西运城044000
出版物刊名： 运城学院学报
页码： 31-35页
年卷期： 2014年 第5期
主题词： 平板折叠桌 参数方程 桌脚边缘线 桌面边缘线
摘要：本文研究平板折叠桌的制作原理,通过数学模型来描述平板折叠桌的设计参数及动态变化过程。

利用空间位置关系和相似三角形,用桌面边缘线的参量与状态变量表示钢筋与木条接触点、木条高低两端的坐标,获得桌脚线在动态过程中的含参变量方程。

同时利用获得的坐标关系求出开槽长度。

并从材料价格、开槽费用及稳定性三方面,分析优化的折叠桌设计加工参数,从而提高折叠桌的稳定性,并使其加工方便且用材最少。

创意平板折叠桌的数学模型大纲本文主要研究的是创意平板折叠桌的设计加工问题，对设计加工参数进行解析和优化并为公司开发设计折叠桌软件供应数学模型，为解决这些问题建立不同样的数学模型并用 MATLAB进行模型求解。

针对问题一，本文建立了模型Ⅰ——动向变化及数学描述模型。

利用解析几何求出每根桌腿由平铺状态到完好张开过程中转过的角度来描述折叠桌动向变化过程，并在此基础上用 MATLAB解出设计加工参数 : 桌腿木条开槽长度 K i，三维空间桌脚边缘线。

针对问题二，本文建立模型Ⅱ ——设计加工参数模型。

采用多目标决策解析方法使产品到达坚固性好、加工方便、用材最少，所以开槽长度K 和长方形平板面积S 必定达到最小，对于任意给定的高度H 和圆形桌面直径 R 确定：①决策变量： a1〔桌面最外侧木条的半长〕， 1 〔最外侧桌腿的竖直偏角〕，p 〔最外侧折叠处到钢筋地址距离与最外侧桌腿的比值〕②目标函数 : K ( 开槽总长度 ) ， S 长方形木板面积用 MATLAB求解出多组方案并确定目标函数最小的最优方案，列出设计加工参数。

针对问题三，本文建立了模型Ⅲ——软件设计模型。

依照客户设定的高度、桌面边缘线形状大小为客户供应三种桌面形状：①圆形桌面，②圆弧和矩形组合桌面，③“8〞字形桌面。

对于圆形桌面可参照模型Ⅱ；对于组合桌面，可在模型Ⅱ的基础上经过增大最外侧桌面木条的长度a1来实现；对于“8〞字形桌面那么可将两个组合桌面的直线边进行对接，所以模型三的建立和求解即可在模型Ⅱ 的基础上改动来实现。

要点词：解析几何MATLAB 多目标决策解析EXLINK1.问题重述某公司生产一种可折叠的桌子，桌面呈圆形，桌腿随着铰链的活动能够平摊成一张平板。

桌腿由假设干根木条组成，分成两组，每组各用一根钢筋将木条连接，钢筋两端分别固定在桌腿各组最外侧的两根木条上，并且沿木条有空槽以保证滑动的自由度。

桌子外形由直纹曲面组成，造型雅观。

试建立数学模型谈论以下问题：1.给定长方形平板尺寸为120 cm × 50 cm × 3 cm ，每根木条宽2.5 cm，连接桌腿木条的钢筋固定在桌腿最外侧木条的中心地址，折叠后桌子的高度为53 cm。

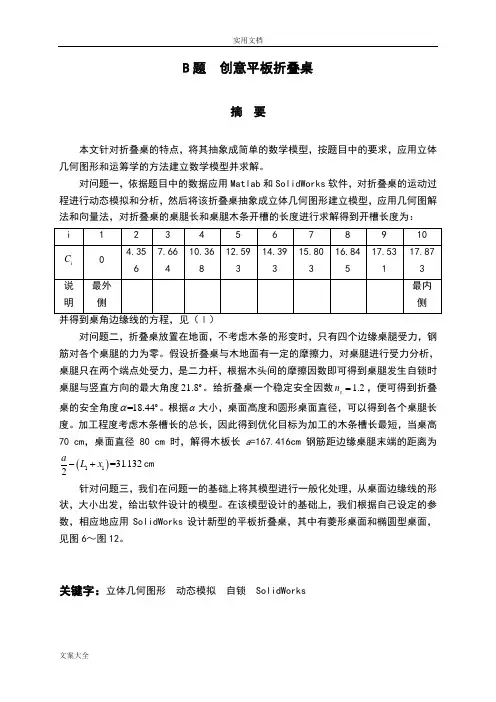
B 题 创意平板折叠桌摘 要本文针对折叠桌的特点，将其抽象成简单的数学模型，按题目中的要求，应用立体几何图形和运筹学的方法建立数学模型并求解。

对问题一，依据题目中的数据应用Matlab 和SolidWorks 软件，对折叠桌的运动过程进行动态模拟和分析，然后将该折叠桌抽象成立体几何图形建立模型，应用几何图解法和向量法，对折叠桌的桌腿长和桌腿木条开槽的长度进行求解得到开槽长度为：对问题二，折叠桌放置在地面，不考虑木条的形变时，只有四个边缘桌腿受力，钢筋对各个桌腿的力为零。

假设折叠桌与木地面有一定的摩擦力，对桌腿进行受力分析，桌腿只在两个端点处受力，是二力杆，根据木头间的摩擦因数即可得到桌腿发生自锁时桌腿与竖直方向的最大角度21.8。

给折叠桌一个稳定安全因数 1.2s n =，便可得到折叠桌的安全角度=18.44α。

根据α大小，桌面高度和圆形桌面直径，可以得到各个桌腿长度。

加工程度考虑木条槽长的总长，因此得到优化目标为加工的木条槽长最短，当桌高70 cm ，桌面直径80 cm 时，解得木板长a =167.416cm 钢筋距边缘桌腿末端的距离为()11=31.1322aL x -+cm 针对问题三，我们在问题一的基础上将其模型进行一般化处理，从桌面边缘线的形状，大小出发，给出软件设计的模型。

在该模型设计的基础上，我们根据自己设定的参数，相应地应用SolidWorks 设计新型的平板折叠桌，其中有菱形桌面和椭圆型桌面，见图6～图12。

关键字：立体几何图形 动态模拟 自锁 SolidWorks一、问题的重述某公司生产一种可折叠的桌子，桌面呈圆形，桌腿随着铰链的活动可以平摊成一张平板（如图1-2所示）。

桌腿由若干根木条组成，分成两组，每组各用一根钢筋将木条连接，钢筋两端分别固定在桌腿各组最外侧的两根木条上，并且沿木条有空槽以保证滑动的自由度（见图3）。

桌子外形由直纹曲面构成，造型美观。

附件视频展示了折叠桌的动态变化过程。

创意平板折叠桌的数学模型摘要本文主要研究的是创意平板折叠桌的设计加工问题，对设计加工参数进行分析和优化并为公司开发设计折叠桌软件提供数学模型，为解决这些问题建立不同的数学模型并用MATLAB 进行模型求解。

针对问题一，本文建立了模型Ⅰ——动态变化及数学描述模型。

利用解析几何求出每根桌腿由平铺状态到完全展开过程中转过的角度来描述折叠桌动态变化过程，并在此基础上用MATLAB 解出设计加工参数:桌腿木条开槽长度i K ，三维空间桌脚边缘线。

针对问题二，本文建立模型Ⅱ——设计加工参数模型。

采用多目标决策分析方法使产品达到稳固性好、加工方便、用材最少，所以开槽长度K 和长方形平板面积S 必须达到最小，对于任意给定的高度H 和圆形桌面直径R 确定：①决策变量：1a （桌面最外侧木条的半长），1 （最外侧桌腿的竖直偏角），p （最外侧折叠处到钢筋位置距离与最外侧桌腿的比值） ②目标函数 :K (开槽总长度)，S 长方形木板面积用MATLAB 求解出多组方案并确定目标函数最小的最优方案，列出设计加工参数。

针对问题三，本文建立了模型Ⅲ——软件设计模型。

根据客户设定的高度、桌面边缘线形状大小为客户提供三种桌面形状：①圆形桌面，②圆弧和矩形组合桌面，③“8”字形桌面。

对于圆形桌面可参照模型Ⅱ；对于组合桌面，可在模型Ⅱ的基础上通过增大最外侧桌面木条的长度1a 来实现；对于“8”字形桌面则可将两个组合桌面的直线边进行对接，所以模型三的建立和求解便可在模型Ⅱ的基础上改动来实现。

关键词：解析几何 MATLAB 多目标决策分析 EXLINK1.问题重述某公司生产一种可折叠的桌子，桌面呈圆形，桌腿随着铰链的活动可以平摊成一张平板。

桌腿由若干根木条组成，分成两组，每组各用一根钢筋将木条连接，钢筋两端分别固定在桌腿各组最外侧的两根木条上，并且沿木条有空槽以保证滑动的自由度。

桌子外形由直纹曲面构成，造型美观。

试建立数学模型讨论下列问题：1. 给定长方形平板尺寸为120 cm × 50 cm × 3 cm，每根木条宽2.5 cm，连接桌腿木条的钢筋固定在桌腿最外侧木条的中心位置，折叠后桌子的高度为53 cm。

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》（以下简称为“竞赛章程和参赛规则”，可从全国大学生数学建模竞赛网站下载）。

我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛章程和参赛规则的，如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛章程和参赛规则，以保证竞赛的公正、公平性。

如有违反竞赛章程和参赛规则的行为，我们将受到严肃处理。

我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： B我们的报名参赛队号为（8位数字组成的编号）：27027006所属学校（请填写完整的全名）：宝鸡文理学院参赛队员(打印并签名) ：指导教师或指导教师组负责人(打印并签名)：李晓波（论文纸质版与电子版中的以上信息必须一致，只是电子版中无需签名。

以上内容请仔细核对，提交后将不再允许做任何修改。

如填写错误，论文可能被取消评奖资格。

）日期： 2014年 09 月 15 日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：对创意平板折叠桌的最优化设计摘要本文主要研究了创意平板折叠桌的相关问题。

对于问题一，首先，我们根据所提供的已知尺寸的长方形平板和桌面形状，桌高的要求，以圆桌面中心作为原点建立了相应的空间直角坐标系，分别求出了各个桌腿的长度，根据在折叠过程中，钢筋穿过的每个点距离桌面的高度相同这一性质，利用MATLAB程序计算出了每根木棒卡槽的长度和桌脚底端每个点的坐标，其中卡槽长度依次为（从最外侧开始，单位：cm）：0、 4.3564、7.663、10.3684、12.5926、14.393、15.8031、16.8445、17.5314、17.8728，并且根据底端坐标拟合出了桌脚边缘线的方程并进行了检验。

1、已知平板尺寸和高度，如何将抽象的描述动态变化过程这一问题数学化？
动态变化过程可以表述为曲线方程问题，其要点是参量的选取，哪些变量在整个折叠过程中是变化的？通过这些变量就能清晰的了解平板变化到桌子的过程。

在此基础上，给出设计加工参数。

开槽长度和桌角边缘线是肯定的描述的，同时可以引入其他变量，如角度等等，可以参照剪式铰的公式增加需要的参量。

第一问切记，要用数学模型和数学描述。

2、三个目标：稳固性好、加工方便、用材最少。

任意给定桌子高度和桌面直径，求平板尺寸和折叠桌的最优加工参数，切记，是最优加工参数；用哪些指标呢？简单举例：平板尺寸（材料最少）、钢筋位置（稳固性好）、开槽长度（加工方便），也可以根据需要自己增加；多目标规划问题，可以用很多方法来解，函数表达式要合理。

3、已知高度和桌面边缘线、桌角边缘线，求解平板尺寸和加工参数。

第三问需要在前两问的基础上进行整合，并建立数学模型。

自己设计的创意折叠桌就各凭本领了。

贯穿3个问题的主线是桌子的基本构架：长方形平板的尺寸和桌子的高度，这两个参量肯定存在着某种联系，而这两个参量的联系又与稳固性好、加工方便、用材最少密不可分。

具体到怎么做，就要看各个参赛队伍的想法了。

B题建模很重要，主要看模型，所以在模型上要多下功夫。

同时，也不要忽视了桌子本身的结构、角度、力学原理等问题，都可能扩展做题思路。

作者： 杨兆兰
作者机构： 兰州文理学院师范学院,甘肃兰州730000
出版物刊名： 求知导刊
页码： 25-26页
年卷期： 2016年 第9期
主题词： 平板折叠桌 开槽长度 直纹曲面 旋转运动
摘要：随着住宅空间的变小,越来越多折叠家具出现,因此许多设计公司制造出了各式各样的折叠家具以满足市场需求,折叠桌作为一种低碳、环保、节能、健康的使用家具,在不少家庭迅中速推广与普及.本文用数学模型模拟出折叠桌的动态变化过程,对折叠桌的设计加工给出了具体的数学描述.。

创意平板折叠桌建模布慧楠1402214026侯爽1402214025张力琨1402214041摘要折叠家具突破传统家具的设计模式，通过折叠可以将面积或体积较大的物品尽量压缩。

细细品味，会发现一种独特的美感，更别说他们还无一例外地兼具到了实用主义。

或拥有灵活自由的使用方式，或功能多样化，为居室腾出不少空间。

某公司设计了一款折叠桌，并以此为背景提出了三个问题，本文利用受力分析、几何知识、以及非线性优化模型等解决了问题。

针对问题一，给定了给定了一块木板的长度、宽度和高度、木条的宽度，以及折叠桌的高度，利用折叠桌的对称性，以任一桌脚为原点，建立空间直角坐标系通过几何模型观察桌面与桌脚木条角度的关系，计算出每条桌角木条顶点处的坐标。

利用Matlab程序，画出桌脚边缘线的变化。

最后根据桌角边缘线的变化，画出折叠桌的动态变化。

针对问题二，针对稳定性好、加工方便、用料最少三个限制条件求出非线性规划的目标函数和限制函数。

由于要求稳定性好，所以桌子应该能承受最大的力量。

在保证稳定性的条件下，如何用最少的木条和选择最佳设计加工参数。

针对问题三，公司开发出一种折叠桌设计软件，根据客户任意设定的折叠桌长度、高度、桌面边缘线的形状大小、桌脚边缘线的大致形状，给出所需材料的形状、尺寸，以及切实可行的加工参数。

最后，对建立的模型和求解方式做一个客观评价，并指出改进方式。

关键字：折叠桌非线性规划目标规划受力分析1、问题重述1.1引言创意折叠木制品为了表现木制品的优雅和设计师所要表达的优雅和功能性。

为了增大有用面积，将木板的宽为直径做圆的直径，将剩余部分成了若干长短不同的木条。

分别用两根钢筋固定两侧的木条，使用者只需提起木板两侧，便可在重力作用下成为桌子。

1.2问题的提出（1）给定长方形平板尺寸120 cm ×50 cm ×3 cm，每根木条宽2.5 cm，连接桌腿木条的钢筋固定在桌腿最外侧木条的中心位置，折叠后桌子的高度为53 cm。