电子科大随机过程与排队论01

电子科技大学计算机学院导师及其科研能力介绍为方便大家报考我们学校,了解各位导师的学术和科研能力,科大考研网www.**将提供给大家详细的信息。

陈雷霆,1966年7月出生,男,现任电子科技大学计算机学院副教授、副院长,主管学院的科研、产业和外事工作,在职博士研究生;现为中国软件行业协会理事,四川省计算机学会理事。

主要研究方向:(1)信息安全;(2)网络多媒体与虚拟现实。

主要科研项目:国家“863-317-403”项目—综合业务多媒体通讯终端与系统;“八五”军事预研项目激光成像雷达系统;多媒体安全监控系统;“九五”军事预研项目激光防撞雷达系统;总装备部项目军用移动图象采集压缩传输系统;航空科技信息集成处理系统;模拟实战射击训练系统;国家“十五”863信息安全项目等。

开设研究生课程:多媒体技术及应用、计算机图形学、软件认证;本科生课程:多媒体技术、数字逻辑。

--------------------------------------------------------------------------------李毅超,男,1969年6月,硕士,副教授。

1997年4月毕业于电子科技大学,获计算机应用硕士学位。

现任网络安全基础实验室主任,计算机网络与通信研究室主任,计算机网络与安全技术研究所副所长,兼成都市软件行业协会副秘书长。

研究方向为计算机网络与通信、网络信息安全、嵌入式应用。

参加或主持"恩威网络MIS系统“、“420驻厂军代室光纤网络MIS系统”、“路由器开发”、信产部基金项目“IP电话网关”,成都华易“美视数字录像监控系统”、西部网信“软交换关守和IP电话多功能终端研发”等近10个科研项目,获得四川省科技三等奖1项,省部级科技成果鉴定5项,国家版权局软件著作权2项。

出版《计算机网络》教材1本在国内外重要刊物和国际会议上发表论文十余篇。

为本科和硕士生开设了若干课程。

获得Microsoft、Novell、SCO、Cisco、Compaq等各大公司认证证书和授权讲师资格。

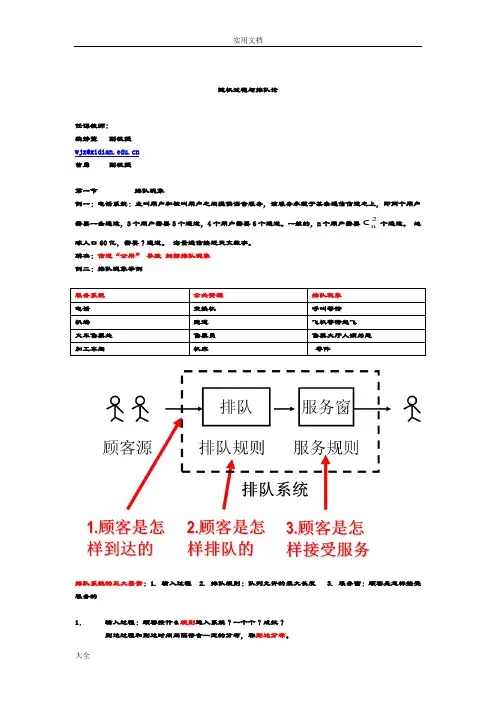
随机过程与排队论任课教师:魏静萱副教授wjx@曾勇副教授第一节排队现象例一：电话系统：主叫用户和被叫用户之间提供语音服务，该服务承载于某条通信信道之上，即两个用户c个通道。

地需要一条通道，3个用户需要3个通道，4个用户需要6个通道。

一般的，n个用户需要2n球人口60亿，需要？通道。

海量通信接近天文数字。

解决：信道“公用”导致拥挤排队现象例二：排队现象举例排队系统的三大要素：1. 输入过程 2. 排队规则：队列允许的最大长度 3. 服务窗：顾客是怎样接受服务的1．输入过程：顾客按什么规则进入系统？一个个？成批？到达过程和到达时间间隔符合一定的分布，称到达分布。

假设：到达过程和到达时间是独立同分布的。

到达过程假定为平稳的，对时间是齐次的。

注：Markov 齐次过程 如果一个过程只依赖于现在，而不是过去。

表1 输入过程的三种随机过程描述按顾客到达过程的不同概率特性分类： ① 定长输入（D ）：顾客等间隔到达，nc τ=n τ的分布函数为 1()()0n t c F t P t t cτ≥⎧=≤=⎨<⎩②Poisson 流输入(M): 系统的输入过程{M(t)>0}是Poission 流 满足4个条件：a) M(t)取值为非负数b) P(M(0)=0)=1, 即时间间隔为0时到达系统 的人数为0 c) 过程{M(t)} 具有平稳独立增量性 d) 每一个增量M(a+t)-M(a)非负，且服从参数为tλ的泊松分布(){()()}!k a t P M t a M a k e K λλ-+-==③ k 阶Erlang 输入(Ek)④ 一般独立输入(G)：顾客的到达过程{n τ}是独立同分布的随机变量序列，其分布函数可以是任意函数。

⑤ 成批到达系统：顾客一批批到达系统，每批相继到达的时间间隔为上述各种分布之一。

2．排队与服务规则① 损失制 （无排队队列）：顾客到达时，系统被占用，顾客离去，不再回来。

第一章随机过程 1
第一章随机过程
本章主要内容：
随机过程的基本概念
●随机过程的数字特征
●随机过程的微分和积分计算
●随机过程的平稳性和遍历性
●随机过程的相关函数及其性质
●复随机过程
●正态分布的随机过程
第一章我们介绍了随机变量，随机变量是一个与时间无关的量，随机变量的某个结果，是一个确定的数值。

例如，骰子的6面，点数总是1～6，假设A面点数为1，那么无论你何时投掷成A面，它的点数都是1，不会出现其它的结果，即结果具有同一性。

但生活中，许多参量是随时间变化的，如测量接收机的电压，它是一个随时间变化的曲线；又如频率源的输出频率，它随温度变化，所以有个频率稳定度的范围的概念（即偏离标称频率的最大范围）。

这些随时间变化的
随机变量就称为随机过程。

显然，随机过程是由随机变量构成，又与时间相关。

§2.3 泊松过程2.3.1 计数过程在客观世界中,存在这样一类随机现象,它们发生的时间、地点或者相联系的某些属性, 常可归属于某空间I中点的随机发生, 这种点的发生就构成随机点过程.12在天文，地理，物理，生物，通信，医学，计算机网络，密码学等许多领域中的如下问题：用盖格记数器记录某类粒子的到达；共同特点: 关心某个事件A 按时间顺序出现的情况. 电话交换机接到的呼唤事件；通信系统运行中出现的误码；细胞中染色体发生的交换；航空公司接受到的托运订单，…将事件A 第i 次发生记为事件A i , 则构成了一个随机事件列A 1, A 2, …, 称为随机事件流, 也称随机点过程.3EX.1一天中某电话交换台接收到的呼叫形成一个随机点过程. 每一次呼叫发生的时间即一个随机点, 此点过程的一条现实(样本函数)是一个时间的序列,其中},,,{21N t t t ,24021≤<<<<N t t t t n 是n 次呼叫发生的时间,N 则是一天中呼叫发生的次数.工程中对于随机点过程, 常需要关注它的计数性质.EX.2 某系统在t时刻开始运行, 在指定的时间段[t0, t+T]内考虑系统因故障停止运行这一事件. 假定系统出故障后能立即修复并继续运行, 则系统在时间区间[t0, t+T]内因出故障而停止运行这些事件构成随机点过程.工程中对于随机点过程, 常需要关注它的计数性质.45(1)N ( t )取非负整数值，且N (0)=0;若用N (t )表示在[0, t ]内出现点的总数, 则有以下特点：(2) 如果s < t ，则N ( s )≤N ( t )；(4) 若, 记43210t t t t <<<<),,(211t t I =),(432t t I =21I I ∪则在集合中发生点的个数为)]()([)]()([3412t N t N t N t N --+)s )t (3)对于s < t, N (t )－N (s )表示时间(s, t ]内发生点的个数；6(1) N (I )是取非负整数值的随机变量, 且N (φ)=0；(2) 对任意, 若,则T I I ⊂21,φ=21I I ∩)()()(2121I N I N I I N +=∪定义2.3.1设是一个随机过程, T =R n . }),({T I I N ⊂}0:{≥=t t T {(),0}N t t ≥特别当计数过程记为称为伴随随机点过程的计数过程(Counting Process).{(),}N I I T ⊂若N (I )表示集合I 中随机事件A 发生的总数，即对任意集合满足2.3.2泊松过程的数学模型及定义Poisson过程是一类很重要的计数过程.一、Poisson过程数学模型在数字通信中误码率λ是重要指标，设{N( t ), t≥0}为时间段[0, t)内发生的误码次{N( t ), t≥0}是计数过程.数,分析:78(1) 初始时刻不出现误码是必然的, (2) 在互不相交的各区间n n n t t t t t t t t <<<<− 2112110),,[,),,[),,0[出现的误码数应互不影响(相互独立), 在系统稳定运行的条件下, 在相同长度区间内出现k 个误码概率应相同,通信系统中误码计数过程{N ( t ), t ≥0}是平稳独立增量过程.故N ( t )为独立增量过程;故可认为N ( t )是平稳增量过程;故N (0)=0;(3) 对足够小Δt时间内出现一个误码的可能性与区间长度成正比是合理的, 即有P{N(Δt)=1}=λΔt+o(Δt), λ>0；(4) 假定对足够小的Δt时间内,出现两个以上误码的概率是关于Δt的高阶无穷小也是合理的, 有P{N(Δt)≥2}=o(Δt).终上所述, 通信系统中误码计数过程{N( t ), t≥0}有以下特点:9101) 零初值性N ( 0)=0;2) 独立增量性;3)齐性(平稳性)4）普通性终上所述, 通信系统中误码计数过程{N ( t ), t ≥0}有以下特点:在(s, t )时间内出现的误码次数仅与时间间隔长度t －s 有关，而与起始时间s 无关;在充分小的时间间隔内误码个数多于一次的概率很小.定义2.3.2 设计数过程{N( t ), t≥0} 满足：(1) N(0)=0;(2) 具有平稳独立增量；(3) P{N(h)=1}=λh+o(h), λ>0；(4) P{N(h)≥2}=o(h).称{N( t ),t≥0)是参数(或速率,强度)为λ的齐次泊松过程.数字通信误码计数过程{N( t ), t≥0} 即一个齐次泊松过程.1112泊松过程广泛存在于工程问题中. 记0(){()0}p h P N h ==),(}1)({)(1h o h h N P h p +===λ),()(}2)({2h o h p h N P k k ==≥∑∞=注：由定义中的条件(3)和(4) 可得,,2,1,0})({)(===k k h N P h p k ，刻画了泊松过程的事件A 发生的稀有性. 对充分小的h >01().h o h λ=−+13定理2.3.1 若{N (t ), t ≥0}是齐次泊松过程，则对任意0≤s ≤t , 随机变量N (t )－N (s )服从参数为λ(t －s )的泊松分布, 即),2,1,0(,!)]([})]()({[)( =−==−−−k e k s t k s N t N P s t kλλ证:因齐次泊松过程具有平稳增量和零初值(){()}k p t P N t k ==00{()()},P N t t N t k =+−=1o 由条件(2)～(4)，当k = 0{()(0)}P N t N k =−=0,1,2,k =14P 0(t+h )=P {N (t+h )=0}= P {N (t )=0}P {N (t+h )－N (t )=0}增量独立=P 0(t ) P 0(h )000()()()()P t h P t o h P t h hλ+−⇒=−+00()()0, dP t P t h dt λ⎧=−⎪→⎨⎪⎩令得.0,)(0≥=λ−t e t p t 解得00(){()}{()()},k p t P N t k P N t t N t k ===+−==P {N (t )=0,N (t+h )－N (t )=0｝=P 0(t )[1－λh +o(h )]0(0)1,P =((1)(0)0)N =条件152o 当k ≥1, 根据全概率公式有)()()()()(110h p t p h p t p h t p k k k −+=+t](t+h ])()()()1()(1h o t hp t p h h t p k k k ++−=+−λλ1()()()()()k k k k P t h P t o h P t P t h hλλ−+−⇒=−++=→dt t dP h k )(,0得令)()(1t P t P k k −+−λλ16=→dt t dP h k )(,0得令)()(1t P t P k k −+−λλ两边同乘以e λt 后移项整理得）（*)()]([1t p e dtt P e d k t k t −=λλλ当k=1, 则10[()]()t t t t d e P t e P t e e dt λλλλλλλ−⎧===⎪⎨⎪⎩1(),0.t p t te t λλ−=≥解得1(0)0P =171(),0t p t te t λλ−=≥解得成立假设t k k e k t t P λλ−−−−=)!1()()(11代入(*)式有)!1()()()]([11−==−−k t t p e dt t P e d k k t k t λλλλλ()t k e P t λ⇒=C k t k +!)(λ）（*)()]([1t p e dt t P e d k t k t −=λλλ利用初始条件可证得,0)0(=k P t kk e k t t P λλ−=!)()(18利用初始条件可证得,0)0(=k P t k k e k t t P λλ−=!)()(对一切k ≥0均成立.定理证明反之亦然.若具有零初值性计数过程{N (t ), t ≥0}满足),2,1,0(,!)]([})]()({[)( =−==−−−k e k s t k s N t N P s t k λλ(齐性)19则有{()1}{()(0)1}1!h h P N h P N h N e −==−==λλ(2){()2}!k h k h P N h ek ∞−=≥=∑λλ应用定义2.3.2 ,可得以下定理.(3)(4)),2,1,0(,!)]([})]()({[)( =−==−−−k e k s t k s N t N P s t kλλ[1()]()h h o h h o h =−+=+λλλ(2)[()][1()]()2!h o h h o h o h =+−+=λλ20定理2.3.2 计数过程{N (t ), t ≥0}是强度为λ的齐次泊松过程, 当且仅当(1)N (0)=0；(3)对一切0≤s <t , N (t )－N (s )～P (λ(t －s )),即),2,1,0(,!)]([})]()({[)( =−==−−−k e k s t k s N t N P s t k λλ(2)N (t )是独立增量过程；泊松过程的等价定义：21EX.3 设{N ( t ), t ≥0}是参数为λ的泊松过程,事件A 在(0,τ)时间区间内出现n 次,试求:P {N (s )=k N (τ)=n }, 0<k<n, 0<s<τ})({})(,)({n N P n N k s N P ====ττ原式解{(),()()}P N s k N N s n k τ==−=−n k n s k s e n k n s e k s e −−−−−−−−=)(!)!()]([!)()(λττλλλττλλk n k s s k n k n −⎟⎠⎞⎜⎝⎛τ−⎟⎠⎞⎜⎝⎛τ−=1)!(!!1,k n k k n s s C ττ−⎛⎞⎛⎞=−⎜⎟⎜⎟⎝⎠⎝⎠0,1,2,,.k n = !()n n e λτλτ−⋅222.3.3 泊松过程的分布及数字特征若{N ( t ), t ≥0}是参数为λ的泊松过程,利用其零初值性和齐性, 有0>∀t 对N (t )～P (λt )其一维分布:})]0()({[})({k N t N P k t N P =−==[],(0,1,2,)!k t t e k k λλ−== ()=u ,t ϕ()R u ,t eiu e t ∈+∞<≤−01λ23二维概率分布:()(){}kj ,t s k t N ,j s N P ≤<==()()()(){}j k s N t N ,j N s N P −=−=−0()(){}()(){}j k s N t N P j N s N P −=−=−=0()()[]()()s t j k s j e !j k s t e !j s −−−−−−=λλλλ()()()t j k j k e !j k !j s t s λλ−−−−=24均值函数t t N E t m λ==)}({)(t t N E )}({=λ有称λ为事件的平均到达率.,0>∀t 因对N (t )～P (λt ).方差函数t t D λ=)(均方差函数C(s,t )=λmin(s,t )，相关函数R (s,t )=λmin(s,t )+λ2st .数字特征25C(s,t )=λmin(s,t )，R (s,t )=λmin(s,t )+λ2st .证:因泊松过程{N ( t ), t ≥0)是平稳独立增量过程，不妨设t > s >0R (s,t )=E {N (t )N (s )}== E {N (s )[N (t )－N (s )]}+E [N 2(s )]sts s s s t s 22])([)(λλλλλλ+=++−×=t t N E t m λ==)}({)(()D t tλ=2(,)(,)()()C s t R s t m s m t s st s tλλλλ=−=+−⋅事实上，应用性质1.3.1即可得.E {N (s )[N (t )－N (s )+ N (s )]}。

电子科技大学计算机学院导师及其科研能力介绍为方便大家报考我们学校,了解各位导师的学术和科研能力,科大考研网www.**将提供给大家详细的信息。

陈雷霆,1966年7月出生,男,现任电子科技大学计算机学院副教授、副院长,主管学院的科研、产业和外事工作,在职博士研究生;现为中国软件行业协会理事,四川省计算机学会理事。

主要研究方向:(1)信息安全;(2)网络多媒体与虚拟现实。

主要科研项目:国家“863-317-403”项目—综合业务多媒体通讯终端与系统;“八五”军事预研项目激光成像雷达系统;多媒体安全监控系统;“九五”军事预研项目激光防撞雷达系统;总装备部项目军用移动图象采集压缩传输系统;航空科技信息集成处理系统;模拟实战射击训练系统;国家“十五”863信息安全项目等。

开设研究生课程:多媒体技术及应用、计算机图形学、软件认证;本科生课程:多媒体技术、数字逻辑。

--------------------------------------------------------------------------------李毅超,男,1969年6月,硕士,副教授。

1997年4月毕业于电子科技大学,获计算机应用硕士学位。

现任网络安全基础实验室主任,计算机网络与通信研究室主任,计算机网络与安全技术研究所副所长,兼成都市软件行业协会副秘书长。

研究方向为计算机网络与通信、网络信息安全、嵌入式应用。

参加或主持"恩威网络MIS系统“、“420驻厂军代室光纤网络MIS系统”、“路由器开发”、信产部基金项目“IP电话网关”,成都华易“美视数字录像监控系统”、西部网信“软交换关守和IP电话多功能终端研发”等近10个科研项目,获得四川省科技三等奖1项,省部级科技成果鉴定5项,国家版权局软件著作权2项。

出版《计算机网络》教材1本在国内外重要刊物和国际会议上发表论文十余篇。

为本科和硕士生开设了若干课程。

获得Microsoft、Novell、SCO、Cisco、Compaq等各大公司认证证书和授权讲师资格。

§1.2 随机过程的数字特征在实际应用中,很难确定出随机过程的有限维分布函数族.过程的数字特征能反映其局部统计性质,在许多实际问题和理论问题中都能很好地满足研究目的.在某些特定情况下, 随机过程的数字特征可以完全确定其有限维分布.需确定各类数字特征随时间的变化规律.12∫+∞∞−∈==T t x xdF X E t m t t ,)()(ˆ)(为此过程的均值函数.定义1.2.1设和是两个实随机过程, 称}),({T t X t ∈ω}),({T t Y t ∈ω1,),()()(−=∈+=j T t jY X Z t t t ωωω为复随机过程.定义1.2.2给定实随机过程, 称}),({T t X t ∈ω1.2.1均值函数与方差函数3复随机过程的均值函数定义为Tt Y jE X E t m t t Z ∈+=,)()(ˆ)(定义1.2.3给定随机过程, 称{}T t X t ∈,2)}({)(ˆ)(t m X E X D t D t t −==为过程的方差函数.称为过程的均方差函数.)(t D 复随机过程的方差函数定义为.},)({ˆ)(2Z T t t m Z E t D t Z ∈−=4)]([)]([)(Z t m Y j t m X t m Z Y t X t t −+−=−因).()(})]({[})]({[)(22t D t D t m Y E t m X E t D Y X Y t X t Z +=−+−=故一般而言, 均值函数和方差函数是时间的函数.问题均值函数和方差函数分别表征了随机过程的什么特征？复随机过程的方差函数定义为.},)({ˆ)(2Z T t t m Z E t D t Z ∈−=5方差函数描述了随机过程在各时点处的波动程度.仅描述了各个孤立时点过程的状态特征. 均值函数表征了随机过程在各时间点上的平均特征.问题均值函数和方差函数分别表征了随机过程的什么特征？描述不同时刻过程状态的关联关系？6需要研究在两个不同时点随机过程状态间的关联关系.回顾两个随机变量的相关系数)()()()()()()(),(Y D X D Y E X E XY E Y D X D Y X Cov XY −==ρ刻画了随机变量X 与Y 的线性相关程度. 1.2.2 协方差函数与相关函数(相关系数)7以下引入的数字特征都是刻画两个不同时点随机过程状态之间的线性关联程度.定义1.2.4给定随机过程,s , t ∈T ,称}),({T t X t ∈ω)(σ)(σ),(ˆ),(t s X X Cov t s t s =ρ为过程的自相关系数函数. 称{})]()][([),(ˆ),(t m X s m X E X X Cov t s C t s t s −−==为过程的协方差函数.8称)(ˆ),(t s X X E t s R =为过程的自相关函数.重点研究内容2)]([),()(t m X E t t C t D t −==有(,)(,)()()C s t R s t m s m t =−特别当时0)(≡t m 零均值随机过程),(),(t s R t s C =对于复随机过程tt t jY X Z +=9自相关函数为)(ˆ),(t s Z Z Z E t s R =协方差函数为]})()][({[),(ˆ),(t m Z s m Z E Z Z Cov t s C Z t Z s t s −−==Ex.1 设U , V 是两个相互独立随机变量, 均服从标准正态分布N (0, 1)，构成随机过程,≥+=t Vt U X t 计算过程的均值函数、方差函数及相关函数，并给出过程的一维和二维分布.对于复随机过程tt t jY X Z +=10解因,0)()(==V E U E 1)()(==V D U D 故均值函数为0,0)()(][)(≥=⋅+==t t V E U E X E t m t 方差函数为222)()(][)(Vt U E t m X E t D t +=−=0,1)()(2)(2222≥+=++=t t V E t UV tE U E U , V 相互独立Ex.1 设U , V 是两个相互独立随机变量, 均服从标准正态分布N (0, 1)，构成随机过程,≥+=t Vt U X t11)(),(),(t s X X E t s R t s C ==)])([(Vt U Vs U E ++=0,,1)()()()(22≥+=+++=t s st V stE UV E t s U E 因)1,0(~2t N Vt U X t ++=故过程的一维概率密度为,,)1(21)()1(2222≥∈+=+−t R x et x f t xt π二维概率密度参见教材P17.协方差函数为12Ex.2(教材P9例1.1.1) 随机开关系统过程..2,cos 21R t tt X t ∈⎩⎨⎧===ωωωωπ出现反面；出现正面求该过程的均值函数,方差函数,相关函数,协方差函数.X (t )cos πt 2tp1/2 1/2解因对任意实数t ∈R, 有;cos 21)()(X t t X E t m t +==π;2cos 21)(222t t X E t +=ππ2221()()()(cos );2X tX D t E X m t t t =−=−注意到X s 与X t 不相互独立, 联合分布律为..2,cos 21R t tt X t ∈⎩⎨⎧===ωωωωπ出现反面；出现正面14s t s t X X E t s R t s X 2221cos cos 21)(),(××+==ππ.2cos cos 21ts s t +ππ=协方差函数为)()(),(),(t m s m t s R t s C −=)cos 21)(cos 21(]2cos cos 21[t t s s ts s t ++−+=ππππts t ss t s t +−−=ππππcos 2cos 2cos cos 41(X (t ),X (s ))(cos πt, cos πs ) (2t, 2s )p 1/2 1/215Ex.3随机振幅周期矩形波5.0}1{}1{===−=X P X P 设是振幅为常数C , 周期为L 的矩形波信号. 另有随机变量X , 其分布律为}0),({≥t t x 对任意t ≥0, 令, 过程称为随机振幅周期矩形波, 试求其均值函数, 方差函数以及自相关函数.)(t x X X t ⋅=}0,{≥t X t16]5.0)1(5.0)[())(()()(=⋅−+===t x t Xx E X E t m t ),(),(t s R t s C =)]()([)(t Xx s Xx E X X E t s ⋅==)()()(2X E t x s x =)()(t x s x =解周期矩形波{x (t )}2222()()[()]()()()t D t D X E Xx t x t E X x t ====)(t x X X t ⋅=5.0}1{}1{===−=X P X P17Ex.4设复随机过程,1∑==nk tj k t k eA Z ω其中为相互独立服从正态N (0,σk 2)的实随机变量,ωk 为常数, 试求m Z (t ), R Z (t 1,t 2).n k A k ,2,1, =解∑∑==+==nk k k k nk tj k t t j t A eA Z k 11)sin (cos ωωω∵∑∑==+=nk n k k k k k tA j t A 11sin cos ωω18]sin []cos [))((11=+=∴∑∑==n k nk k k k k t A E j t A E t Z E ωω22)(,,,2,1,kk k A E n k A σ==且相互独立因 ωω12121211(,)()[()()]k k nnj t j t Z t t k k k k R t t E Z Z E A eA e====∑∑ωω11cos sin nnt k k k k k k Z A t j A t===+∑∑∑∑==−=n k nl t t j k l k eA E 11)(][21ωω∑=−=nk t t j k k eA E 1)(221)(ω∑=−=nkttjk keAE1)(221)(ω∑=−=nkttjk ke1)(221ωσ∑=−+−=nkkkkttjtt121212)(sin)((cosωωσ思考题：为什么说随机过程的均值函数和自相关函数在研究过程的概率与统计特性尤其重要?19201.2.3 多维随机过程及互相关函数类似于多维随机向量的概念，实际问题中常需要研究多维随机过程.Ex.5随机传输系统输入随机过程X t ，在系统L 的作用下，其输出为随机过程Y t .研究输入与输出过程间的相互关系，分析其整体统计特性.21Ex.6 n 台计算机通过一个有带宽限制的路由器获取网络数据,第i 台计算机获取数据的速度是随机过程:ni t X i t ,,2,1},0,{)( =≥需研究各台计算机的速度之间的关联关系.22定义1.2.5设给定概率空间(Ω,F , P )和指标集T , 若对每个t ∈T, 有定义在(Ω,F , P )上的随机向量,ω∈Ω与之对应. 称）ω，，ω，ω)()()(()()2()1(n t t t X X X },)()()({()()2()1(T t X X X n t t t ∈）ω，，ω，ω 为n 维随机过程.可定义多个随机过程的联合分布函数.参见教材P21.23工程实践中常需要研究多维随机过程的不同过程在相同或不同时点处的关联关系.},0,{≥t X t },0,{≥t Y t st引进两个随机过程的互相关函数.s X tX s Y24定义1.2.7 给定两个复随机过程},{)1(T t Z t ∈称和},,{)2(T t Z t ∈),(Cov ),()2()1()2()1(t s Z Z Z Z t s C =})]([)]({[)2()1()2()1(s m Z s m Z E Z t Z s −−=为两个随机过程的互协方差函数.][),()2()1()2()1(t s Z Z Z Z E t s R =为两个随机过程的称画指标.25当时间s 和t 变动, 两个过程的互协方差函数和互相关函数反映了它们之间的整体相关程度.对实随机过程和},{T t X t ∈},{T t Y t ∈)()(),(),(Cov ),(T m s m Y X E Y X t s C Y X t s t s XY −==若对任意s , t ∈T),(=t s C XY )()()()()(t s Y X t s Y E X E T m s m Y X E ==或称两个过程互不相关.26若对任意s , t ∈T)(),(==t s XY Y X E t s R 称两个过程正交.Ex.6设随机系统输入信号是随机过程输出过程是带有噪声的过程，即},{T t X t ∈Tt N X Y t t t ∈+=,其中是噪声过程.计算输出过程的均值函数与相关函数.},{T t N t ∈27解)()()()()()(t m t m N E X E Y E t m N X t t t Y +=+==)})({(),(t t s s Y N X N X E t s R ++=),(),(),(),(t s R t s R t s R t s R N NX XN X +++=特别当与相互正交,则},{T t X t ∈},{T t N t ∈),(),(),(t s R t s R t s R N X Y +=Ex.6设随机系统输入信号是随机过程输出过程是带有噪声的过程，即},{T t X t ∈Tt N X Y t t t ∈+=,其中是噪声过程.计算输出过程的均值函数与相关函数.},{T t N t ∈28Ex.7已知实随机过程的自相关函数为R (s , t ), 令},{T t X t ∈t a t t X X Y −=+求自相关函数R YY (s , t ).解])[(),(t s a s YY Y X X E t s R −=+),(),(t s R t a s R XY XY −+=)]([)(),(t a t s t s XY X X X E Y X E t s R −==+),(),(t s R a t s R −+=代入),(),(),(),(),(t s R a t s R t a s R a t a s R t s R YY ++−+−++=29),(),(),(),(),(t s R a t s R t a s R a t a s R t s R YY ++−+−++=特别取s=t ,则)(])[(),(2t t a t YY Y D X X E t t R =−=+),(),(),(),(t t R a t t R t a t R a t a t R ++−+−++=Ex.7已知实随机过程的自相关函数为R (s , t ), 令},{T t X t ∈t a t t X X Y −=+求自相关函数R YY (s , t ).。