随机过程在排队论中的应用

马尔可夫过程与排队论马尔可夫过程与排队论是数学中重要的两个概念，它们在统计学、概率论、运筹学等领域中有着广泛的应用。

本文将分别介绍马尔可夫过程和排队论的基本概念和应用。

马尔可夫过程是一个随机过程，其特点是未来的状态只与当前状态有关，与过去的状态无关。

这种性质被称为马尔可夫性。

马尔可夫过程是由状态空间和转移概率矩阵组成的。

状态空间是一组离散或连续的状态，转移概率矩阵描述了不同状态之间的转移概率。

马尔可夫过程的一个重要应用是在排队系统中的模拟和分析。

排队论是研究排队系统的数学方法和技术的学科。

排队系统是指由顾客和服务员组成的系统，顾客需要接受服务，而服务员有一定的处理能力。

排队论主要关注以下几个方面的问题：平均等待时间、系统繁忙率、系统的稳定性等。

排队论通过数学建模，提供了一种分析和优化排队系统的方法。

在排队系统中，马尔可夫过程可以用来描述系统的状态变化。

例如，一个银行的柜台服务系统可以看作是一个排队系统。

顾客到达银行后，根据柜台服务员的繁忙情况，决定是否需要排队等待。

排队等待时，顾客处于等待状态；当柜台服务员空闲时，顾客进入服务状态。

这个过程可以用马尔可夫过程来描述，其中状态空间包括顾客的等待状态和服务状态，转移概率矩阵描述了顾客在不同状态之间的转移概率。

马尔可夫的应用广泛，不仅在排队系统中有着重要作用，还在许多其他领域中有着广泛应用。

例如，马尔可夫链被用于自然语言处理中的语言模型，通过学习上下文的转移概率来预测下一个词的概率。

马尔可夫过程还被用于金融领域的风险管理，通过建立市场模型来预测金融资产的价格变动。

排队论也有许多重要的应用。

在制造业中，排队论可以用于优化生产线的运作效率，减少等待时间，提高资源利用率。

在交通领域，排队论可以用于交通信号控制系统的优化，减少拥堵现象。

在电信业中，排队论可以用于优化无线网络的资源分配，提高用户的通信质量。

总结来说，马尔可夫过程与排队论是数学中重要的两个概念。

马尔可夫过程描述了一个随机过程的状态变化，而排队论则应用了马尔可夫过程来分析和优化排队系统。

基于随机过程和排队论的客流量预测模型研究客流量预测是城市规划、交通管理和商业运营等领域重要的决策依据。

在过去几十年中，随机过程和排队论被广泛应用于客流量预测模型的研究和实践中。

本文将基于随机过程和排队论，探讨客流量预测模型的研究。

首先，介绍客流量预测的背景和意义。

客流量预测是指利用历史数据、实时采集的数据和其他相关信息，通过建立合理的数学模型和算法，对未来一段时间内的客流量进行预测。

这对于交通拥堵缓解、公共汽车和地铁的调度优化、商场的运营决策等都具有重要的意义。

其次，介绍随机过程在客流量预测中的应用。

随机过程是指一类随机变量组成的数列或随机函数，它们的值随时间的推移而变化。

在客流量预测中，可以使用随机过程来对客流量的变化进行建模。

例如，可以使用马尔可夫链来描述人群在不同地点之间的转移概率和持续时间，进而预测未来的客流量。

然后，介绍排队论在客流量预测中的应用。

排队论是研究排队系统的数学理论，可以帮助我们理解和优化排队现象。

在客流量预测中，可以使用排队论来模拟和分析客流量的到达和服务过程。

例如，可以使用M/M/1模型来预测某一时刻的客流量、平均排队长度和平均等待时间。

接下来，介绍基于随机过程和排队论的客流量预测模型的研究进展。

目前，已经有许多研究基于随机过程和排队论的方法提出了各种客流量预测模型。

这些模型包括马尔可夫链模型、M/M/1模型、基于时间序列的模型等。

其中，基于时间序列的模型在实际应用中较为常见，可以利用历史客流量数据进行参数估计和模型拟合，进而预测未来的客流量。

最后，总结基于随机过程和排队论的客流量预测模型的优点和不足。

随机过程和排队论能够提供可靠的理论基础和数学方法，帮助我们对客流量进行准确的预测和分析。

然而，这些模型往往依赖于许多假设和条件，对于复杂的客流量预测问题可能存在不足之处。

未来的研究可以进一步改进和拓展基于随机过程和排队论的客流量预测模型，提高其准确性和实用性。

综上所述，基于随机过程和排队论的客流量预测模型是客流量预测的重要研究方向。

概率论中的随机过程耦合方法随机过程耦合方法在概率论中起着重要的作用。

本文将介绍随机过程的基本概念以及耦合方法的原理和应用。

首先，我们将对随机过程进行定义和分类，然后介绍随机过程的性质，包括马尔可夫性、齐次性和平稳性。

接下来，我们将介绍随机过程的耦合方法，包括部分耦合和全耦合，以及它们的应用领域。

最后，我们将给出一些相关的例子和实际应用。

一、随机过程的定义和分类随机过程是一类随机变量的集合，这些随机变量的取值与时间有关。

根据时间的连续性和取值的离散性，随机过程可以分为连续时间随机过程和离散时间随机过程。

连续时间随机过程指的是时间可取无限多个值的情况，而离散时间随机过程指的是时间只能在有限的时间点上取值的情况。

二、随机过程的性质1. 马尔可夫性：随机过程在任意时刻的状态只与前一时刻的状态有关，与过去的状态无关。

这种性质称为马尔可夫性。

具有马尔可夫性的随机过程可以用马尔可夫链来描述。

2. 齐次性：随机过程的统计特性在时间上是不变的，即在不同时刻的状态转移概率是相同的。

这种性质称为齐次性。

3. 平稳性：随机过程的统计特性在时间上是相同的，即对任意时间间隔，它们的概率分布是相同的。

这种性质称为平稳性。

三、随机过程耦合方法随机过程耦合方法是一种通过联结多个随机过程来分析它们的性质的方法。

耦合方法可以分为部分耦合和全耦合两种。

1. 部分耦合：部分耦合是指将多个随机过程中的部分变量进行关联，使它们具有一定的联系。

通过部分耦合方法，可以分析随机过程的边界行为、极限特性等。

例如，在排队论中，可以通过耦合方法来研究排队系统中的稳定性和瓶颈效应。

2. 全耦合：全耦合是指将多个随机过程完全关联起来，使它们的演化趋势相同。

通过全耦合方法，可以研究随机过程的整体特性、大数定律等。

例如，在传播模型中，可以通过全耦合方法来研究信息传播的速度和范围。

四、随机过程耦合方法的应用随机过程耦合方法在概率论和统计学中有广泛的应用。

以下是一些典型的应用领域：1. 排队论：研究排队系统中的稳定性、服务能力和平均等待时间等。

随机过程与排队论在运输与物流管理中的应用与优化
随机过程与排队论是运输与物流管理中常用的数学工具，它们的应用可以帮助我们优化物流运输的效率和成本。

首先，随机过程可以用来描述物流运输中的不确定性。

物流运输过程中，往往会受到各种因素的影响，例如天气、交通状况、货物数量等等。

这些因素的变化会导致物流运输的时间和成本的波动，因此需要使用随机过程来建立模型，预测物流运输的时间和成本，并进行优化。

其次，排队论可以用来优化物流运输中的排队问题。

在物流运输中，往往会出现货物等待装卸的情况，这就需要排队论来分析和优化。

排队论可以帮助我们确定最佳的货物装卸顺序和数量，以最大程度地减少货物等待时间和成本。

除了以上两个方面，随机过程和排队论还可以应用于货车调度、仓库管理、供应链优化等方面。

通过建立数学模型，我们可以预测货车到达时间、货物储存位置、供应链中各环节的效率等等，从而优化物流运输的效率和成本。

总之，随机过程和排队论在运输与物流管理中有着广泛的应用和优化空间。

我们可以通过建立数学模型来预测和优化物流运输的效率和成本，从而提高企业的竞争力和盈利能力。

概率论中的随机过程耦合方法应用在概率论中，随机过程是一个随机变量集合，可以描述随机事件在时间上的演变过程。

随机过程是理解和研究许多实际问题的重要工具。

其中，随机过程的耦合方法是一种在不同的随机过程之间建立联系的数学技术，可以用于解决各种问题。

本文将介绍概率论中的随机过程耦合方法的应用。

一、随机过程耦合方法的基本概念随机过程的耦合方法是一种用于将两个或多个随机过程联系起来的方法。

通过随机过程的耦合，我们可以在不同的时间和空间范围内分析它们之间的关系。

这种方法提供了一种强大的工具，可以研究随机性的传播和传递，以及随机过程之间的相互影响。

二、随机过程耦合方法在随机游走中的应用随机游走是一种离散的、随机的过程，可以用来模拟随机事件在某个空间上的演化。

通过耦合方法，我们可以将两个或多个随机游走联系起来，研究它们之间的传播过程。

例如，在金融领域，我们可以使用随机过程耦合方法来分析两个或多个股票的价格演变，并预测它们之间的相互关系。

三、随机过程耦合方法在排队论中的应用排队论是研究排队系统的数学理论。

在排队系统中，有多个顾客同时到达，需要等待服务。

通过耦合方法，我们可以将两个或多个排队系统联系起来，研究它们之间的互动和影响。

例如，在交通规划领域，我们可以使用随机过程耦合方法来分析不同道路上的车辆流量，研究它们之间的交互作用，以及对整体交通流量的影响。

四、随机过程耦合方法在随机矩阵中的应用随机矩阵是一种随机过程耦合方法的重要应用。

随机矩阵是一种随机变量的矩阵表示，可以用于描述多个相关的随机事件。

通过耦合方法，我们可以将两个或多个随机矩阵联系起来，研究它们之间的相互作用。

例如，在通信系统中，我们可以使用随机过程耦合方法来分析多个天线之间的传输信道，并评估它们之间的干扰程度。

五、随机过程耦合方法在可靠性理论中的应用可靠性理论是研究系统可靠性和故障概率的数学理论。

通过耦合方法，我们可以将两个或多个系统联系起来，研究它们之间的可靠性。

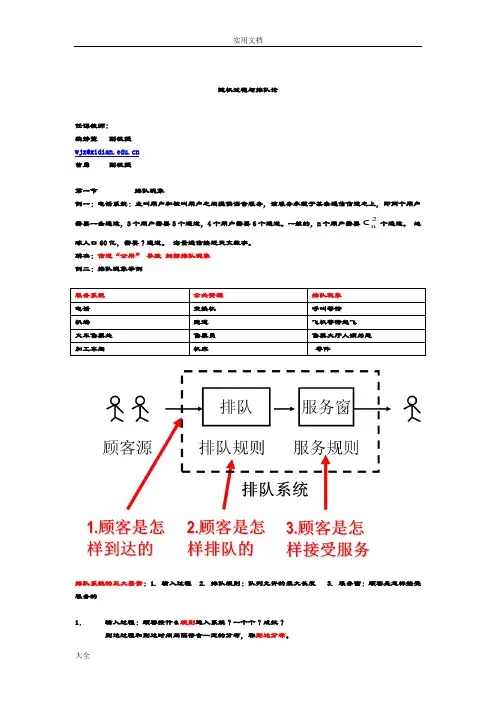
随机过程与排队论任课教师:魏静萱副教授wjx@曾勇副教授第一节排队现象例一：电话系统：主叫用户和被叫用户之间提供语音服务，该服务承载于某条通信信道之上，即两个用户c个通道。

地需要一条通道，3个用户需要3个通道，4个用户需要6个通道。

一般的，n个用户需要2n球人口60亿，需要？通道。

海量通信接近天文数字。

解决：信道“公用”导致拥挤排队现象例二：排队现象举例排队系统的三大要素：1. 输入过程 2. 排队规则：队列允许的最大长度 3. 服务窗：顾客是怎样接受服务的1．输入过程：顾客按什么规则进入系统？一个个？成批？到达过程和到达时间间隔符合一定的分布，称到达分布。

假设：到达过程和到达时间是独立同分布的。

到达过程假定为平稳的，对时间是齐次的。

注：Markov 齐次过程 如果一个过程只依赖于现在，而不是过去。

表1 输入过程的三种随机过程描述按顾客到达过程的不同概率特性分类： ① 定长输入（D ）：顾客等间隔到达，nc τ=n τ的分布函数为 1()()0n t c F t P t t cτ≥⎧=≤=⎨<⎩②Poisson 流输入(M): 系统的输入过程{M(t)>0}是Poission 流 满足4个条件：a) M(t)取值为非负数b) P(M(0)=0)=1, 即时间间隔为0时到达系统 的人数为0 c) 过程{M(t)} 具有平稳独立增量性 d) 每一个增量M(a+t)-M(a)非负，且服从参数为tλ的泊松分布(){()()}!k a t P M t a M a k e K λλ-+-==③ k 阶Erlang 输入(Ek)④ 一般独立输入(G)：顾客的到达过程{n τ}是独立同分布的随机变量序列，其分布函数可以是任意函数。

⑤ 成批到达系统：顾客一批批到达系统，每批相继到达的时间间隔为上述各种分布之一。

2．排队与服务规则① 损失制 （无排队队列）：顾客到达时，系统被占用，顾客离去，不再回来。

排队系统的符号表述描述符号：①/②/③/④/⑤/⑥各符号的意义：①——表示顾客相继到达间隔时间分布，常用以下符号：M——表示到达的过程为泊松过程或负指数分布；D——表示定长输入；EK——表示K阶爱尔朗分布；G——表示一般相互独立的随机分布。

②——表示效劳时间分布，所用符号与表示顾客到达间隔时间分布一样。

③——表示效劳台(员)个数：“1〞表示单个效劳台，“s〞(s>1)表示多个效劳台。

④——表示系统中顾客容量限额，或称等待空间容量。

如系统有K个等待位子，那么，0<K<∞，当K=0时，说明系统不允许等待，即为损失制。

K=∞时为等待制系统，此时一般∞省略不写。

K为有限整数时，表示为混合制系统。

⑤——表示顾客源限额，分有限与无限两种，∞表示顾客源无限，一般∞也可省略不写。

⑥——表示效劳规那么，常用以下符号FCFS：表示先到先效劳的排队规那么；LCFS：表示后到先效劳的排队规那么；PR：表示优先权效劳的排队规那么。

二、排队系统的主要数量指标描述一个排队系统运行状况的主要数量指标有：1．队长和排队长(队列长)队长是指系统中的顾客数(排队等待的顾客数与正在承受效劳的顾客数之和)；排队长是指系统中正在排队等待效劳的顾客数。

队长和排队长一般都是随机变量。

2．等待时间和逗留时间从顾客到达时刻起到他开场承受效劳止这段时间称为等待时间。

等待时间是个随机变量。

从顾客到达时刻起到他承受效劳完成止这段时间称为逗留时间，也是随机变量。

3. 忙期和闲期忙期是指从顾客到达空闲着的效劳机构起，到效劳机构再次成为空闲止的这段时间，即效劳机构连续忙的时间。

这是个随机变量，是效劳员最为关心的指标，因为它关系到效劳员的效劳强度。

与忙期相对的是闲期,即效劳机构连续保持空闲的时间。

在排队系统中，忙期和闲期总是交替出现的。

4．数量指标的常用记号(1)主要数量指标L——平均队长，即稳态系统任一时刻的所有顾客数的期望值；L q——平均等待队长，即稳态系统任一时刻等待效劳的顾客数的期望值；W——平均逗留时间，即(在任意时刻)进入稳态系统的顾客逗留时间的期望值；W q——平均等待时间，即(在任意时刻)进入稳态系统的顾客等待时间的期望值。

随机过程在排队论中的应用有哪些排队论是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法。

它在各个领域都有着广泛的应用，如通信系统、交通运输、计算机网络、生产制造等。

而随机过程作为一种描述随机现象随时间演变的数学工具，在排队论中发挥着至关重要的作用。

随机过程为排队论提供了精确的数学模型。

以最简单的单服务台排队系统为例，顾客到达的时间间隔和服务时间通常都是随机的。

我们可以用泊松过程来描述顾客的到达过程，用指数分布来描述服务时间。

泊松过程具有无记忆性，即过去的到达情况不影响未来的到达概率，这与实际中许多顾客到达的随机现象相符。

指数分布的无记忆性也使得它能很好地模拟服务时间的不确定性。

通过这些随机过程模型，我们能够计算出排队系统的各种性能指标，如平均排队长度、平均等待时间、系统利用率等。

在多服务台排队系统中，随机过程的应用更加复杂但也更加关键。

例如，假设我们有多个服务台并行工作，顾客到达后按照一定的规则选择服务台。

这时，我们可能需要用到更复杂的随机过程，如马尔可夫链来描述系统的状态转移。

马尔可夫链假设系统在某一时刻的状态只与前一时刻的状态有关，而与更早的历史无关。

通过构建合适的状态空间和转移概率矩阵，我们可以分析系统的稳态性能和瞬态性能。

随机过程还能帮助我们优化排队系统的设计和运营策略。

以银行的服务窗口为例，如果已知顾客到达的规律和服务时间的分布，我们可以利用随机过程的理论来确定最优的服务台数量，以平衡服务成本和顾客等待成本。

此外，还可以通过调整服务规则，如优先服务某些类型的顾客，或者采用预约制度等，来改善系统的性能。

这些优化决策都需要基于对排队系统随机行为的准确建模和分析，而随机过程为我们提供了这样的工具。

在通信领域，随机过程在排队论中的应用尤为突出。

例如，在网络数据包的传输中，数据包的到达和传输时间都是随机的。

我们可以用排队论来分析网络的拥塞情况，评估不同的流量控制策略和路由算法的效果。

通过随机过程模型，我们能够预测网络的性能指标，如丢包率、延迟时间等，从而为网络的设计和优化提供依据。

排队论的基本原理：
排队论（Queuing Theory）是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法，其基本原理主要包括以下几个方面：
1.排队系统的组成：排队系统通常由输入过程、排队规则和服务机构三个部分组成。

输入过程是指顾客到达服务系统的随机方式，排队规则是指顾客到达后按照怎样的规则排队等待服务，服务机构则是指服务的提供方式。

2.概率论和随机过程：排队论中需要用到概率论和随机过程的数学知识，如概率分布、
期望、方差等。

这些知识用于描述顾客到达和服务时间的统计规律。

3.状态分析：排队论中的状态分析主要是指对排队系统的状态进行描述和分类，如空
闲状态、忙状态等。

通过对状态的分析，可以确定系统的各种性能指标，如等待时间、队长等。

4.最优化原理：排队论中的最优化原理是指通过调整系统参数，如服务时间、服务速
率等，使得系统的性能指标达到最优。

最优化原理的目的是在满足一定约束条件下，使系统的某种性能指标达到最优。

5.可靠性理论：可靠性理论是排队论中的一个重要组成部分，它研究的是系统可靠性
的概念、指标和计算方法。

可靠性理论可以帮助我们分析系统的可靠性、故障率和可用性等方面的问题，为系统的设计和优化提供依据。

随机过程应用应用随机过程解决实际问题随机过程应用：应用随机过程解决实际问题随机过程是概率论中的一种重要的数学工具，用于描述随机变量随时间变化的过程。

随机过程的应用非常广泛，可以解决许多实际问题。

本文将探讨随机过程的应用，并介绍其中一些实际问题的解决方法。

一、排队论排队论是随机过程应用的一个重要领域，用于解决有关排队问题的数学模型。

排队问题广泛存在于我们的日常生活中，比如银行、超市等地的排队现象。

通过排队论的分析，可以确定最优的队列长度、服务台数量等，以提高服务效率。

二、信号处理随机过程在信号处理中也有广泛的应用。

在无线通信中，信号通常会受到噪声的干扰，而随机过程可以用来描述这些干扰的统计特征。

通过对随机过程进行分析，可以提高信号处理的效果，减小噪声对信号质量的影响。

三、金融工程随机过程在金融工程领域也有着重要的应用。

股票价格、利率等金融变量通常都是随机变量，它们的变化过程可以用随机过程来描述。

通过对随机过程进行建模和分析，可以预测未来的金融市场走势，为投资决策提供参考。

四、优化问题在一些优化问题中，随机过程也发挥着关键的作用。

比如在生产调度中，将任务分配给不同的机器，机器故障时间也可用随机过程来描述。

通过对随机过程的优化分析，可以提高生产效率，降低成本。

五、风险评估风险评估是许多领域中的一个重要问题，而随机过程可以用来对风险进行评估和预测。

比如在保险行业，通过对随机过程的分析，可以评估不同风险事件的发生概率，从而合理确定保险费率。

六、物理系统建模在物理系统的建模中，随机过程也是一个重要的工具。

比如在材料科学中，材料的疲劳寿命通常也是一个随机变量，可以用随机过程来描述。

通过对随机过程的分析，可以预测材料的寿命，从而制定合理的材料使用方案。

综上所述，随机过程在许多领域中都有着广泛的应用。

从排队论到金融工程，从信号处理到优化问题，从风险评估到物理系统建模，随机过程都为解决实际问题提供了有力的工具和方法。

随机过程简介随机过程这一 学科最早起源于对物理学的研究 ，如吉布斯（美国物理化学家、数 学物理学家）、玻尔兹曼（奥地利物理学家）、庞加莱（法国数学家）等人对统计力学的研究，及后来爱因斯坦、维纳（Wiener ，美国数学家，控制论的创始人 卜莱维（Levy ，法国数学家）等人对布朗运动的开创性工 作。

1907年前后，马尔可夫（Markov ）研究了一系列有特定相依性的随机变量，后人称之为 马尔可夫链。

1923年维纳给出布朗运 动的数学定义，直到今日这一过程仍是重要的研究课题。

随机过程一般理论的研究通常认为开始于 20世纪30年代。

1931年，柯尔莫哥洛夫发表了 《概率论的 解析方法》，1934年辛饮发表 了《平稳过程的相关理论》，这 两篇著作奠定了马尔可夫过程与 平 稳过程的理论 基础。

1953年，杜布出版了名著《随机过程论》，系统且严格地叙述了随机过程基 本理论。

一般认为，随机过程整个学科的理论基础是由 柯尔莫哥洛夫（Kolmogorov ）和杜布（Doob ）奠定的。

柯尔莫哥洛夫1903年4月25日，柯尔莫哥洛夫出生于俄罗斯 年去世。

他的 母亲出身于贵族家庭，在他出生后 10天去世。

他只好由二位和指导学习。

这一数学规律 。

研究范围的坦博夫城。

他的父亲在 1919姨妈抚育他5、6岁时就 归纳出了“丰1人2 , 1+3 =22 , 1+3+5=3人2 , 1+3+5+7 =4A2 .…”14岁时他就开始自学高等数学,冶金，后来转 学数学， 1920 大学三年级时就发表了年他高中 论文。

毕业，进入莫斯科大学, 先学习1925 年大学毕业 1929 年研究生毕 1935 年获得苏联 后，当研究生。

业后，担任莫斯科大学数学力学 首批博士学位。

研究所助理研究员。

1931 1933 年起他担任 年担任莫斯科大学数学力学研究所所长 莫斯科大学教授，并指导研究生 创建了概率论、数理统计、数，先后教过数学分析、 论、数理逻辑和信息论等课程。

随机过程与排队理论基础随机过程和排队理论是概率论中重要的研究领域，它们在现代科学和工程领域中有着广泛的应用。

随机过程是一种随机变量随时间变化的数学模型，而排队理论则是研究在服务系统中顾客到达、服务和离开的规律和性能的理论。

一、随机过程的基本概念在随机过程中，随机变量是定义在一个概率空间上的函数，通常用来描述系统在不同时间点的状态。

随机过程可以分为离散时间和连续时间两种类型。

离散时间随机过程可以理解为在离散时间点上取值的随机变量序列，而连续时间随机过程则是一个在连续时间上取值的随机变量的集合。

随机过程的一个重要性质是马尔可夫性质，即未来的状态只依赖于当前状态，与过去状态无关。

这种性质在很多实际问题中都有应用，如信道传输、股票价格模型等。

二、排队理论的基本原理排队理论是描述一定规则下队列中顾客到达、服务和离开的数学理论。

其中，排队系统由顾客到达过程、服务过程和排队规则三部分组成。

排队理论的研究重点在于通过建立数学模型，分析系统性能指标如平均等待时间、队列长度等，以优化系统效率。

排队理论中最常用的模型是M/M/1模型，其中M表示到达的随机过程服从泊松分布，服务时间的随机过程也服从指数分布，1表示只有一个服务通道。

这个模型简单而有效，可以推广到更复杂的多通道模型。

三、随机过程与排队理论的应用随机过程和排队理论广泛应用于信息技术、通信网络、交通系统、生产制造等领域。

在信息技术中，网络数据包的到达和处理就可以通过排队模型来分析和优化。

在交通系统中，排队理论可以用来研究车辆的拥堵情况和道路的负载能力。

总的来说，随机过程和排队理论为我们理解和优化复杂系统提供了重要的工具和方法，它们的研究将会继续对科学技术的发展产生深远影响。

HUNAN UNIVERSITY 排队买票过程
1.实验原理
排队问题是日常生活中常遇到的现象，与我们生活密不可分，如本次实验我们要做的——队列长度无限制的火车站窗口排队买票过程。

排队现象的要素包括两个方面的内容：一是需要接受服务的顾客；二是提供服务的服务台。

最近几十年来，排队理论在计算机网络、通信、交通以及其它公共事业
领域的应用越来越广泛，已成为分析和设计这些系统的一个不可或缺的工具。

本实验采用蒙特卡洛模拟方法，蒙特卡洛是一种应用随机数来进行计算机模拟的方法。

此方法对研究的系统进行随机观察抽样，通过对样本值的观察统计，求得所研究系统的某些参数。

在MATLAB中发生指数分布的随机数命令为exprnd()，产生均匀分布随机数命令。

2.实验目标
1、了解排队论，通过对每个个别的随机服务现象的统计研究，找出反映这些
随机现象平均特性的规律。

2、通过实例掌握简单的离散事件系统模拟的基本方法及其MATLAB实现方法。

3.实验设计
实验代码：
实验结果：
图为到达时间与离开时间对比图
图为等待时间和停留时间对比图
4.总结
通过本次实验让我看到用Matlab软件求解排队系统模型问题是非常简明扼要的，不用考虑计算公式和细节问题，只需按照代码和基本参数就能得到我们做实验时所关注的排队问题的主要数量指标即可。

利用软件模拟有助于我们对时机问题抽象模型的理解。

连续随机过程和离散随机过程
首先，让我们来看看连续随机过程。

连续随机过程是指在连续时间范围内随机变量的演化。

这种过程通常用随机变量的连续函数来描述，比如布朗运动就是一个典型的连续随机过程。

这种过程在金融领域、通信领域以及物理学中都有着广泛的应用。

例如，在金融领域中，股票价格的变化可以被描述为连续随机过程，而在通信领域中，信道的噪声也可以被建模为连续随机过程。

接下来，我们来看看离散随机过程。

离散随机过程是指在离散时间范围内随机变量的演化。

这种过程通常用随机变量的序列来描述，比如马尔可夫链就是一个典型的离散随机过程。

这种过程在排队论、信道编码等领域有着重要的应用。

例如，在排队论中，顾客到达和离开的过程可以被建模为离散随机过程，而在通信领域中，信道的状态转移也可以被描述为离散随机过程。

总的来说，连续随机过程和离散随机过程都是描述随机变量演化的重要工具，它们在不同的领域和应用中都有着广泛的应用。

对于理解和分析随机系统的行为，深入理解这两种随机过程是非常重要的。

在我们的日常生活中，常常遇到资源有限而需要按一定规则排队的情况，例如到超市购物付款，买火车票，数据的传输，电路交换等等，资源的有限性以及服务的随机性是排队现象存在的基础，研究这一类问题具有普遍意义。

数学中，通过随机过程分析来研究排队问题的方法论称为排队论，本文就是利用数学的随机过程理论来分析排队问题，讲述最基本的排队模型，标准的M/M/1 模型，分析代表其系统运行情况的指标。

排队系统一般来说是由等待资源的顾客和提供服务的服务员构成，由于顾客的到达与服务完毕的时间是不确定的，所以排队系统存在随机性。

为了既能保证服务质量又不浪费服务资源，人们在随机过程的基础上发展起来了一种数学方法—排队论。

任何排队系统都有三个基本参数，服务员的数目也称窗口数m ，顾客的到达速率λ，系统的服务速率μ。

除此之外，为了很好的描述系统的运行状态，还要研究顾客到达的时间间隔ti ，以及服务时间τi 的统计分布和排队规则。

最常用的方法也是比较合适的方法是认为它们服从指数分布，因为指数分布具有无记忆性，与现实中的一大类情况相似，并且使得排队过程称为马尔可夫过程。

所以要对排列规则做如下的假设：平稳性：到达k 个顾客的概率只和顾客到达的时间间隔t 有关，与起始时刻无关。

无后效性：顾客到达的时刻无相独立疏稀性：在无限小的时间间隔内，到达两个及以上顾客的概率为0，且在有限时间区间内到达的顾客数是有限的。

上面说做的假设，可以保证顾客到达的时间间隔t 为指数分布的随机变量，在现实生活中的排队系统里上述假设也是成立或者近似成立的。

t 的概率密度函数为 a(t)= λe −λt 式中的λ是顾客的到达率。

可以证明在T 时间间隔内，有k 个顾客到达的概率符合泊松分布：P k (T)=(λT)kk ! e −λT由于已经说明两个顾客服务所需的时间是互不相关的，平稳的，疏稀的，则服务时间τ的分布也服从指数分布b(τ)= μe −μτ类似的，在T 时间内，有k 个顾客被服务后离去的概率为Q k (T)=(μT)k k!e −μT 有了这些基础后，下面开始介绍一种基本的排队模型。

随机过程在通信系统性能分析与优化中应用随机过程在通信系统性能分析与优化中应用随机过程在通信系统性能分析与优化中发挥着重要的作用。

通信系统是指通过各种信号传输介质进行信息交换和传递的系统。

在信息通信技术的发展中，如何提高通信系统的性能一直是一个关键问题。

随机过程作为一种数学工具，可以帮助分析和优化通信系统的性能。

一、随机过程简介随机过程是指一族随机变量的集合，其值依赖于时间或其他参数。

它在时间上的演化是随机的，因此可以用来描述许多实际场景，如无线信道的衰落、用户的到达和离开等。

常见的随机过程有马尔可夫链、泊松过程等。

二、随机过程在通信系统性能分析中的应用1. 随机过程用于信道建模通信系统的性能受到信道影响较大。

随机过程可以用来建立信道模型，从而了解信号在传输过程中发生的随机变化。

以无线通信领域为例，信道通常受到多径衰落、阴影效应和多普勒效应等影响，这些影响可以通过随机过程进行建模。

2. 随机过程用于排队论分析通信系统中的等待时间和服务时间通常呈现出随机性。

随机过程可以用于排队论分析，帮助我们理解系统的稳定性和性能。

通过分析排队论参数，可以优化通信系统的性能，比如减少等待时间、提高系统吞吐量等。

3. 随机过程用于网络协议分析网络协议是实现通信系统的关键组成部分。

随机过程可以用于分析和优化网络协议的性能。

比如在数据链路层，通过建立马尔可夫链模型，可以计算出系统的传输效率和丢包率，从而改进数据链路的可靠性。

4. 随机过程用于流量建模通信系统的性能分析需要充分了解系统中的流量特点。

随机过程可以用于建立流量模型，分析其统计特性。

通过分析流量的波动情况和分布特点，可以合理规划系统资源，提高系统的容量。

三、随机过程在通信系统性能优化中的应用1. 基于马尔可夫决策过程的优化方法马尔可夫决策过程是一种基于状态转移的优化方法。

在通信系统中，可以将系统的性能目标定义为一个马尔可夫过程，并通过状态转移概率和决策规则来优化系统的性能。