当前位置：文档之家 › 第二章 地下水运动的基本微分方程及求解条件

第二章 地下水运动的基本微分方程及求解条件

  • 格式：doc
  • 大小：42.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

地下水动力学(第二章 地下水向河渠的运动-专)

地下水动力学(第二章 地下水向河渠的运动-专)

( ) (
)
任一断面单宽流量： ∂h 上式对x求导，并代入Darcy定律 q = − Kh ∂x 得：
q x ,t K = q x ,0 + ∆ h02,t G x, t − ∆ hl2,t G ′ x, t 2l
[ ( ) ( ) ( ) ( )]
式中：qx,0—x断面处回水前单宽流量； qx,t—x断面处回水后t时刻的单宽流量； G (x, t ) —河渠流量函数；
hx2, 0 = h02, 0 −
h02, 0 − hl2, 0 l
x
(3) 两侧河渠水位同时出现水位上升，发生瞬时回 水，左河水位自h0,0上升至h0,t，右河自hl,0上升至hl,t。 （二）数学模型的建立和求解 如图坐标，可得如下数学模型：
∂ ∂h ∂h K h = µ ∂x ∂x ∂t h 2 ( x,0 ) = h02, 0 − h(0 ,t ) = h0 ,t h(l ,t ) = hl ,t h02, 0 − hl2, 0 l x
d dh W =0 h + dx dx K h x =0 = h1 h x =l = h2
模型求解： W dh d h = − dx 将微分方程化为： dx K 两边不定积分： dh W
h dx =− K x + C1
再化简： 再积分：
W hdh = − xdx + C1dx K
特例， h1=h2
l=2
时， a =
l 2
，代入(2)式，可得
K 2 hmax − h12 W
(
)
可见，当水位条件一定时，在入渗强度愈大和渗 透性愈弱的含水层中，排水渠间距愈小，反之愈大。 (3) 河渠间单宽流量的计算 通用公式： 2 2 当x=0时，得流入左河的单宽流量：

水动力学基本微分方程

水动力学基本微分方程
Q y dy 沿y方向流入单元体的水量： (Qy y 2 )dt
流出： (Q Qy dy)dt y
y 2
沿z方向流入单元体的水量： v2 dx dy dt 流出：v1 dx dy dt
流入量－流出量＝：
Q x x方向： dxdt x
y方向： Q y y dydt
2 H 2 H 2 H s H 2 2 2 K t x y z
２.对于二维的情况，常用 和T表示(
各项均乘以m）
H H H (Tx ) (Ty ) ， x x y y t 2 H 2 H H 当Tx Ty T时, 则 2 2 x y T t
上述分析表明：H降低，承压含水层释 放部分地下水；H增大，承压含水层贮存部 分地下水，这部分水量称为弹性贮存量。
弹性贮水量的大小与含水层的岩性和 结构有关，为了表征含水层弹性释水（储 水）的能力，下面将给出弹性贮水率和贮 水系数的概念。
2.含水层的贮水率和贮水系数
１.贮水率（Specific storativity）用 s 表示
H H H H ( K xx ) ( K yy ) ( K zz ) s x x y y z z t
上式就是非均质各向异性承压含水层中地下水三 维非稳定运动的基本微分方程。对各向异性介质，取 坐标轴方向与主渗透方向一致。
（二）方程的化简和讨论
１.对于均质各向同性含水层，Ｋ为常数，这时 简化为：
a
o
b a dy
x y Ｑx为单位时间内通过abcd断面流入的水量。在dt内，
沿x方向通过abcd断面流入均衡单元的水量 a＇b＇c＇d＇断面从均衡单元流出的水量为
Qx (Qx dx)dt x

《地下水动力学》课程总结

《地下水动力学》课程总结
应用
求水文地质参数
K、T、μ、μ*、B…
计算运动要素
Q、q、H、s、t….
模型识别
判断水文地质条件 如边界性质
1、介质（为描述介质特性提出的一些概念）
连续介质模型-典型单元体 渗透性：
渗透系数（K）、等效渗透系数 均质、非均质 各向同性、各向异性
2、渗流场
渗流特征 运动要素：实际流速、渗透流速、质点流速、单个孔隙
5、水文地质参数及获取方法
渗透系数K 入渗强度W 导水系数T=KM 弹性释水系数μ* 给水度μ 阻越流系数B 压力传导系数a =T/ μ*
配线法 直线图解法 水位恢复资料法
1、达西定律
dH Q = -KA
ds
dH v = -K
ds
适用条件：1<Re<10的层流
2、 Dupuit假定，Dupuit微分方程
Kz
∂ ∂z
s(r, H 0 ,t )
=
-μ
∂ ∂t
s(r, H 0 ,t )
方程解析解
s(r, z, t) Q
4 T
1
0
4
yJ 0
(
y
2
)[ 0
(
y)
n ( y)]dy
n 1
• 纽曼解的特点
5、地下水向不完整井的运动
• 不完整井流特点（三点）
• 地下水向不完整井的稳定运动
井底进水的承压水不完整井（空间汇点法）
井壁进水的承压水不完整井（空间汇线法）
∫ Q
s = 4πK(z2 - z1)
[z2
1
+
z1 (z - η）2 +r 2
1
]dη
(z + η）2 +r 2

第二章地下水运动的基本微分方程及定解条件

第二章地下水运动的基本微分方程及定解条件

第二章一、填空题 1．渗流连续方程是 现。

地下水运动的基本微分方程及定解条件在地下水运动中的具体表 。

2．试写出在忽略含水层骨架压缩情况下的地下水连续方程 3．地下水运动基本微分方程实际上是 时间内从 层在单位时间 方向和 。

、方程，方程的左端表示单位方向进入单元含水层的净水量， 右端表示单元含水4．地下水平面二维、三维流基本微分方向的数学意义分别表示渗流区内 的渗流规律， 它们的物理意义分别表示任一 5．裘布依假设的要点是 直的，流线 体含水层。

7．贮水率的物理意义是：当水头 中由于水 是 ，后者是 ，以及介质骨架的 ，二是释放出 水量。

、 以及 。

时，从 ，而释放（贮存）的 含水层 水 不同，前者 以及没有 。

，高等于 柱 的水量均衡方程。

是铅 ，实际上意味着6．单位面积（或单位柱体）含水层是指量。

贮水系数与贮水率比较，主要差别有两点：一是含水层 水量，后者则完全是 二、判断题 1．对含水层来说其压缩性主要表现在空隙和水的压缩上。

（ 2．贮水率 μt=ρg (α+nβ)也适用于潜水含水层。

（ 3．贮水率只用于三维流微分方程。

（ ） ）不同，前者有疏干重力水和弹性8．在渗流场中边界类型主要分为）4．贮水系数既适用承压含水层，也适用于潜水含水层。

（ （ ） 6．潜水含水层的给水度就是贮水系数。

（ ））5．在一定条件下，含水层的给水度可以是时间的函数，也可以是一个常数。

7．在其它条件相同而只是岩性不同的两个潜水含水层中。

在补给期时，给水 度 µ 大，水位上升大，µ 小，水位上升小，在蒸发期时，µ 大，水位下降大，µ 小，水位下降小。

（ ）8．地下水连续方程和基本微分方向实际上都是反映质量守恒定律。

（9． 地下水三维流基本微分方程 div (K·gradH) = 于潜水。

（ ））m s = ¶H / ¶t 既适用于承压水也适用10．潜水和承压水含水层的平面二维流基本微分方向都是反映单位面积含水 层的水量均衡方程。

地下水动力学第二章

地下水动力学第二章

2.1.3 渗流连续性方程
连续性方程就是质量守恒方程，也称为水均衡方程 水均衡的基本思想：
对某一研究对象，流入－ 流出＝V 研究对象可以是大区域的，也可以是微分单元体
大区域的水均衡计算经常用于区域的水资源评价 本课程基于微分单元体做水均衡，推导渗流连续性方程。
为反映含水层地下水运动的普遍规律，我们选定在各向 异性多孔介质中建立地下三维不稳定流动连续性方程。
渗流连续性方程推导
( v)| x (xx,y,z,t)
X方向流入流出差
(v x )|(x ,y ,z ,t) y z t (v x )|(x x ,y ,z ,t) y z t
y方向流入流出差
(v y ) |( x ,y ,z , t ) x z t (v y ) |( x ,y y ,z , t ) x z t
V
V0 V0
( p0
p)
V V0
( p0
p)
水的压缩方程
dp 1 dV
V
V p
V0
由于V~V0变化不大，故 V p
由于V
m
V
d(m)
dV V
m
d ( 1 ) d
dp 1d
d
dp
多孔介质的压缩方程
假定多孔介质近似地符合弹性变形，依虎克定律，有
d 1 dVb Vb
t
(n z ) ( ze ) z( e e ) t t 1 e 1 e t t
根 据 e(1e)和 dp dH ,得 eep(1e)H
p
t pt
t
根d据 和 dp dH ,得 pH
dp
t pt
t
(nz) z [(1e)HeH]
t 1e

第二章地下水运动的基本微分方程及定解条件

第二章地下水运动的基本微分方程及定解条件

第二章一、填空题 1．渗流连续方程是 现。

地下水运动的基本微分方程及定解条件在地下水运动中的具体表 。

2．试写出在忽略含水层骨架压缩情况下的地下水连续方程 3．地下水运动基本微分方程实际上是 时间内从 层在单位时间 方向和 。

、方程，方程的左端表示单位方向进入单元含水层的净水量， 右端表示单元含水4．地下水平面二维、三维流基本微分方向的数学意义分别表示渗流区内 的渗流规律， 它们的物理意义分别表示任一 5．裘布依假设的要点是 直的，流线 体含水层。

7．贮水率的物理意义是：当水头 中由于水 是 ，后者是 ，以及介质骨架的 ，二是释放出 水量。

、 以及 。

时，从 ，而释放（贮存）的 含水层 水 不同，前者 以及没有 。

，高等于 柱 的水量均衡方程。

是铅 ，实际上意味着6．单位面积（或单位柱体）含水层是指量。

贮水系数与贮水率比较，主要差别有两点：一是含水层 水量，后者则完全是 二、判断题 1．对含水层来说其压缩性主要表现在空隙和水的压缩上。

（ 2．贮水率 μt=ρg (α+nβ)也适用于潜水含水层。

（ 3．贮水率只用于三维流微分方程。

（ ） ）不同，前者有疏干重力水和弹性8．在渗流场中边界类型主要分为）4．贮水系数既适用承压含水层，也适用于潜水含水层。

（ （ ） 6．潜水含水层的给水度就是贮水系数。

（ ））5．在一定条件下，含水层的给水度可以是时间的函数，也可以是一个常数。

7．在其它条件相同而只是岩性不同的两个潜水含水层中。

在补给期时，给水 度 µ 大，水位上升大，µ 小，水位上升小，在蒸发期时，µ 大，水位下降大，µ 小，水位下降小。

（ ）8．地下水连续方程和基本微分方向实际上都是反映质量守恒定律。

（9． 地下水三维流基本微分方程 div (K·gradH) = 于潜水。

（ ））m s = ¶H / ¶t 既适用于承压水也适用10．潜水和承压水含水层的平面二维流基本微分方向都是反映单位面积含水 层的水量均衡方程。

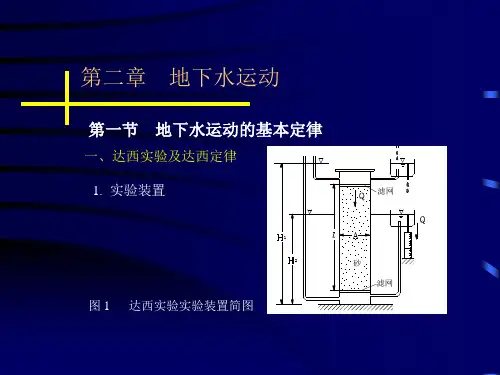
第四讲地下水运动

因此实际的未知量只有6个，
K xz K zx
K zy K yz
对于二维的情况，有
K
K xx
K
yx
K xy
K
yy
(14)
VI zxyx
实际的未知量只有三个.
式（12）表明，在各向异性介质中，x方向的渗透 速度分量，不仅同方向的水力坡度有贡献，而且不 同方向的和也有贡献。即渗透速度矢量v和水力坡 度矢量I不共线，有如图3所示，而在各向同性介质 中二者是共线的。
K xx
K
yy
Kx
Ky 2
Kx
Ky 2
cos 2
K
xy
Kx
Ky 2
sin 2
（19）
其值也可用摩尔园方法求出，见图5。
1
1 1
0
1
反之，如已知ox1y1坐标系上的分量Kxx ,Kxy 和Kyy，求与之交角为α的主轴坐标系oxy上的 主值，可用下式
1
K K
x y
K xx
K yy 2
K xx
——雷诺数(Re)是一个无量纲数,是 1883年雷诺(Osborne Reynolds)在管道 流实验时首先采用
Re Vd
式中 Re──雷诺数； V ──水流平均流速，m/s； d ──管径，m； ν ──水的运动粘滞系数，m2/s。
——流 态
层流（laminar flow) 紊流 (Turbulent flow)
达西和cm2二种单位之间有如下关系：
1da 9.8697109 cm2
da
当参数用渗透率表示时，达西定律有如下形式
V k g dH dS
（11）
引入渗透系数和渗透率概念有何用途？

地下水数值模拟02_地下水运动的数学模型


2
H 0
n 2
——隔水边界
第三类边界条件 H aH b n
例：弱透水边界
K H Hn H 0 n m1 / K1
溶质运移问题的边界条件
第一类边界条件
c(x,
y, z,t) 1

c1(x,
y, z,t)
——给定浓度边界
第二类边界条件 c
Di, j x j ni 2 f2 (xi , t)
u(x, y, z,t) t0 0(x, y, z)
• 2、边界条件
第一类边界条件 u(x, y, z,t) 1 1(x, y, z,t)
第二类边界条件
u n
2
1(x, y, z,t)
第三类边界条件
u



u n
3
3x,
y, z,t
水流问题的边界条件
Reynolds数小于1~10
• 有些情况下，用液体压强表示更为方便
– 例如：油水两相流动
vx

K
H x
vy

K
H y
vz

K
H z
K g k
H z p
g

k p
vx



x
v y


k
p y
vz


k


K ( d
)
dhc
C

t

x
K( )
x


y
K
(

)
y


z
K (

2地下水渗流基本方程及数学模型


安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
*范围值：n×10-3~ n×10-5； 范围值：0.05~ 0.30。实际测出的值往往小于理论值。
上述两参数之间的不同，还在于潜水含水层存在滞后疏干现象。 弹性释水与重力给水: 对于含水层而言，由于受埋藏条件的限制，抽水时，水的给 出存在着不同。 潜水含水层在抽水过程中，大部分水在重力作用下排出，疏干作用于水位变动带（
为反映含水层地下水运动的普遍规律，我们选定在各向异性多孔介 质中建立地下三维不稳定流动连续性方程。
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
由于渗流场中各点的渗流速度大小、方向都不同，为了反映液体运动的 质量守恒关系，需要在三维空间中建立微分方程形式表达的连续性方程。
则有：
即：
将
代入整理得：
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
所以有
上式为三维流微分方程，也可写成：
物理意义：渗流空间内任一单位体积含水层在单位时间内流入与流出该体 积含水层中的弹性水量的变化量，即单位体积含水层的水量均衡方程。
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
= =
由含水层状态方程，
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
因为 则可得到： 所以有 ，Z为定值，则
于是连续性方程变为：

地下水运动定解条件

3 上的Ｈ和
H 的线性组 n
H H n
其中： ， 为已知函数，这种类型的边界 条件称为第三类边界条件或混合边界条件。 第三类边界条件实例（J.Bear）
2015-6-4 10
注意：
1°求解非稳定渗流问题时，数学模型应 包括：支配方程、初始条件和边界条件；
2°而对稳定流问题，数学模型仅有：支 配方程和边界条件。
x2 y 2
H 0 亦为第一类边界；
潜水面任一点的水位已知时，抽水井井壁水位为一类 边界。
2015-6-4 6
（2）第二类边界条件
当已知渗流区某部分边界上的流量分布时，称这 部分边界为第二类边界或给定流量边界。相应的边界 条件表示为：
H H K K n n
ss22
q q11 ( (x x,, y y,, z z,,tt), ), （ （x x,, y y,, z z) ) S S22
5
常见的第一类边界有：
河流或湖泊切割含水层，二者有密切的水力联系，此 时，河湖的水位是已知的，水头 1 或 2是由河湖水位的 统计资料得到的关于t的函数；
泉水溢出带：其标高即为水位资料，但必须保证溢出 带不消失；
区域的抽水井，注水井或疏干巷道也可作为给定水头 边界处理； 无限边界 H ( x, y, t )
H ( x, y, z, t ) t 0 H0 ( x, y, z), （x, y, z) 空间区域
/ 或H ( x, y, t ) t 0 H0 ( x, y), （x, y) D平面区域
Ho ，Ho′为空间和平面区域上已知的水位分布。如 研究平面问题，某一时刻所测的等水位线即可作为初值。
2015-6-4 3
注意： a.初始条件对计算结果的影响，随计算 时间的延长而减弱； b.初始条件并非地下水的原始状态，即 未开发以前的状态； c.初始条件可根据需要任意选取。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章地下水运动的基本微分方程及求解
条件
一、填空题
1. 渗流连续方程是质量守恒定律在地下水运动中的具体表现。

2. 地下水运动基本微分方程实际上是地下水水量均衡方程，方程的左端表示单位时间内从水平方向和垂直方向进入单元含水层内的净水量，右端表示单元含水层在单位时间内质量变化量。

3. 越流因素Ｂ越大，则说明弱透水层的厚度越大，其渗透系数越小，越流量就越小。

4. 单位面积(或单位柱体)含水层是指底面积为一个单位，高等于含水层厚度柱体含水层。

5. 在渗流场中边界类型主要分为水头边界、流量边界以及混合边界。

二、判断题
1. 地下水连续方程和基本微分方程实际上都是反映质量守恒定律。

(√)
2. 潜水和承压水含水层的平面二维流基本微分方程都是反映单位面积含水层的水量均方程。

(√ )
3. 在潜水含水层中当忽略其弹性释放水量时，则所有描述潜水的非稳定流方程都与其稳定流方程相同。

(×)
4. 越流因素B和越流系数σ都是描述越流能力的参数。

(√)
5. 在实际计算中，如果边界上的流量和水头均已知，则该边界既可作为第一类边界，也可作为第二类边界处理。

(√)
6. 凡是边界上存在着河渠或湖泊等地表水体时，都可以将该边界作为第一类边界处理。

(×)
7. 同一时刻在潜水井流的观测孔中，测得的平均水位降深值总是大于该处潜水面的降深值。

(√)
三、分析建模题
1. 一口井位于无限分布的均质、各向同性潜水含水层中，初始时刻潜水水位在水平不透水底板以上高度为H 0（x ，y ），试写出下列两种情况下地下水流向井的非稳定流数学模型（已知水流为二维非稳定流）。

（1）井的抽水量Q w 保持不变；
解：数学模型如下
t H K K Q y H H y x H H x W ∂∂=-⎥⎦
⎤⎢⎣⎡∂∂∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂μ；（x,y ）∈D,t ≥0 ① H （x,y ，0）=H 0（x ，y ）；（x,y ）∈D ，t=0
② H （x,y ，t ）|Γ1=H 0（x ，y ）；（x,y ）∈Γ1,t>0
③ W
r Q n H
T W π2-
=∂∂Γ；（x,y ）∈Γw,t>0（Γw 为井壁） （2）井中水位H w 保持不变。

解：数学模型如下
t
H K y H H y x H H x ∂∂=⎥⎦⎤⎢⎣⎡∂∂∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂μ；（x,y ）∈D,t ≥0 ① H （x,y ，0）=H 0（x ，y ）；（x,y ）∈D ，t=0
② H （x,y ，t ）|Γ1=H 0（x ，y ）；（x,y ）∈Γ1,t>0
③ H （x,y ，t ）|ΓW =H w ；（x,y ）∈ΓW ,t>0（Γw 为井中）
2. 图2-1为某地供水水源地的平面图和水文地质剖面图，已知其开采强度为ε，试根据图示写出开采过程中地下水非稳定流的数学模型。

解：数学模型如下
t
H W y H KH y x H KH x ∂∂=-+⎥⎦⎤⎢⎣⎡∂∂∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂με；（x,y ）∈D,t ≥0 ④ H （x,y ，0）=H 0（x ，y ）；（x,y ）∈D ，t=0 ⑤ H （x,y ，t ）|Γ1=f （x ，y ，t ）；（x,y ）∈Γ1,t>0（Γ为河流边界） ⑥
0=∂∂ΓW n H ；（x,y ）∈ΓW ,t>0（Γw 为隔水边界）。