(完整版)求解共点力平衡问题的常见方法(经典归纳附详细答案),推荐文档
- 格式:pdf
- 大小:394.30 KB
- 文档页数:8

解答共点力平衡问题的常用方法物体的平衡问题,涉及力的概念、受力分析、力的合成与分解、列方程运算等多方面数学、物理知识和能力的应用,是高考中的热点。
一、共点力平衡问题的数学解法1、相似三角形法:如果在对力利用平行四边形定则运算的过程中,力三角形与几何三角形相似,则可根据相似三角形对应边成比例等性质求解。
2、拉密定理若在共点的三个力作用下,物体处于平衡状态,则各力的大小分别与另外两个力夹角的正弦成正比。
3、正交分解法:共点力平衡条件F合=0是矢量方程,通常用正交分解法把矢量运算转化为标量运算,给解题带来方便。
4、函数图象法:利用函数图象分析和解答问题,关键是分析图象的物理意义,进行推理判断和计算。
二、共点力平衡问题的物理方法1、离法与整体法通常在分析外力对系统的作用时,用整体法:在分析系统内各物体间的相互作用时,用隔离法。
二者常需交叉运用,从而优化解题思路和方法,使解题简洁明了。
2、动态平衡问题———图解法利用图解法解决此类问题的基本方法是:对研究对象在状态变化过程中的若干状态进行受力分析,依据某一参量的变化,在同一图中作出物体在平衡状态下的平衡力图(力的平行四边形),再由动态的力的四边形各边长度变化及角度变化,确定力的大小及方向的变化情况,3、临界法:从量变到质变的转变状态,叫临界状态。
分析和解决临界问题,有两种基本方法:一是演绎法———从一般到特殊的推理方法;二是临界法———从特殊到一般的推理方法。
因为临界状态总是比一般状态简单,所以解决临界问题,临界法比演绎法简单。
一般,只要分清物理过程抓住临界状态,确定临界状态,建立临界方程,问题就迎刃而解了。

求解共点力平衡问题的常见方法共点力平衡问题,涉及力的概念、受力分析、力的合成与分解、列方程运算等多方面数学、物理知识和能力的应用,是高考中的热点。
对于刚入学的高一新生来说,这个部分是一大难点。
一、力的合成法物体在三个共点力的作用下处于平衡状态,则任意两个力的合力一定与第三个力大小相等,方向相反;例1. 如图1所示,一小球在纸面内来回振动,当绳OA和OB拉力相等时,摆线与竖直方向的夹角为:()图1A. 15°B. 30°C. 45°D. 60°解析:对O点进行受力分析,O点受到OA绳和OB绳的拉力F A和F B及小球通过绳子对O点的拉力F三个力的作用,在这三个力的作用下O点处于平衡状态,由“等值、反向”原理得,F A和F B的合力F合与F是等值反向的,由平行四边形定则,作出F A和F B的合力F合,如图2所示,由图可知,故答案是A。
二、力的分解法在实际问题中,一般根据力产生的实际作用效果分解。
[例2]如图1所示,用一个三角支架悬挂重物,已知AB杆所受的最大压力为2000N,AC绳所受最大拉力为1000N,∠α=30°,为不使支架断裂,求悬挂物的重力应满足的条件?[分析]悬绳A点受到竖直向下的拉力F=G,这个拉力将压紧水平杆AB并拉引绳索AC,所以应把拉力F沿AB、CA两方向分解,设两分力为F1、F2,画出的平行四边形如图2所示。
[解]由图2可知:因为AB、AC能承受的最大作用力之比为当悬挂物重力增加时,对AC绳的拉力将先达到最大值,所以为不使三角架断裂,计算中应以AC绳中拉力达最大值为依据,即取F2=F2m=1000N,于是得悬挂物的重力应满足的条件为G m≤F2sin30°=500N,[说明]也可取A点为研究对象,由A点受力,用共点平衡条件求解。
A点受三个力:悬挂物的拉力F=G,杆的推力F B,绳的拉力F C,如图4所示。
根据共点力平衡条件,由F C sinα=G,F C cosα=F B,即得共点力平衡条件可以适用于多个力同时作用的情况,具有更普遍的意义。

处理共点力平衡问题得常见方法与技巧物体所受各力得作用线(或其反向延长线)能交于一点,且物体处于静止状态或匀速直线运动状态,则称为共点力作用下物体得平衡。
它就是静力学中最常见得问题,下面主要介绍处理共点力作用下物体平衡问题得一些思维方法。
1、解三个共点力作用下物体平衡问题得方法解三个共点力作用下物体平衡问题得常用方法有以下五种:(1)力得合成、分解法:对于三力平衡问题,一般可根据“任意两个力得合成与第三个力等大反向”得关系,即利用平衡条件得“等值、反向”原理解答。
例1、如图1所示,一小球在纸面内来回振动,当绳OA与OB拉力相等时,摆线与竖直方向得夹角为:( )图1A、 15°B、 30°C、 45°D、 60°解析:对O点进行受力分析,O点受到OA绳与OB绳得拉力F A与F B及小球通过绳子对O 点得拉力F三个力得作用,在这三个力得作用下O点处于平衡状态,由“等值、反向”原理得,F A 与F B得合力F合与F就是等值反向得,由平行四边形定则,作出F A与F B得合力F合,如图2所示,由图可知,故答案就是A。
图2(2)矢量三角形法:物体受同一平面内三个互不平行得力作用平衡时,这三个力得矢量箭头首尾相接,构成一个矢量三角形;反之,若三个力矢量箭头首尾相接恰好构成三角形,则这三个力得合成必为零,因此可利用三角形法,求得未知力。
例2、图3中重物得质量为m,轻细线AO与BO得A、B端就是固定得。
平衡时AO就是水平得,BO与水平面得夹角为。
AO得拉力与BO得拉力得大小就是:( )图3A、B、C、D、解析:因结点O受三力作用而平衡,且与mg垂直,所以三力应组成一个封闭得直角三角形,如图4所示,由直角三角形知识得:,所以选项B、D正确。
图4(3)正弦定理法:三力平衡时,三个力可构成一封闭三角形,若由题设条件寻找到角度关系,则可用正弦定理列式求解。
例3、如图5(a)所示,质量为m得物体用一轻绳挂在水平轻杆BC得C端,B端用铰链连接,C点由轻绳AC系住,已知AC、BC夹角为,则轻绳AC上得张力与轻杆BC上得压力大小分别为多少?图5解析:选C点为研究对象,受力情况如图5(b)所示,由平衡条件与正弦定理可得即得与所以由牛顿第三定律知,轻绳AC上得张力大小为,轻杆BC上得压力大小为。

共点力平衡的七大题型-Word版含解析引言在物理学中,共点力平衡是指当多个力作用在一个物体上时,这些力的合力为零,物体处于平衡状态。
共点力平衡是力学中的基础概念,也是解决各种物理问题的基础。
在本文中,我们将介绍共点力平衡的七大题型,并提供相应题型的解析。
题型一:两个力的平衡题目描述有一个物体,上面有两个力:F1和F2,分别作用在物体上的不同点,使物体处于平衡状态。
已知F1和F2的大小和方向,请问这两个力分别是多少?解析根据共点力平衡的定义,对于两个力的平衡题型,我们可以设立以下方程:F1+F2=0其中,F1和F2表示两个力的大小和方向,这里假设物体在水平方向上运动。
根据方程求解即可得到F1和F2的数值。
题型二:三个力的平衡题目描述有一个物体,上面有三个力:F1、F2和F3,分别作用在物体上的不同点,使物体处于平衡状态。
已知F1、F2和F3的大小和方向,请问这三个力分别是多少?解析对于三个力的平衡题型,我们可以设立以下方程组:$$ \\begin{cases} F1 + F2 + F3 = 0 \\\\ \\sum M = 0\\end{cases} $$其中,F1、F2和F3表示三个力的大小和方向,$\\sumM$表示物体上力矩的和,根据方程组求解即可得到F1、F2和F3的数值。
题型三:四个力的平衡题目描述有一个物体,上面有四个力:F1、F2、F3和F4,分别作用在物体上的不同点,使物体处于平衡状态。
已知F1、F2、F3和F4的大小和方向,请问这四个力分别是多少?解析对于四个力的平衡题型,我们可以设立以下方程组:$$ \\begin{cases} F1 + F2 + F3 + F4 = 0 \\\\ \\sum M = 0\\end{cases} $$同样地,F1、F2、F3和F4表示四个力的大小和方向,$\\sum M$表示物体上力矩的和。
根据方程组求解即可得到F1、F2、F3和F4的数值。
题型四:平衡条件的推导题目描述有一个物体,上面有多个力:F1、F2、…、Fn,分别作用在物体上的不同点,使物体处于平衡状态。

专题 共点力平衡得七大题型目录一、三类常考得“三力静态平衡”问题 (1)热点题型一 三个力中,有两个力互相垂直,第三个力角度(方向)已知。
(1)热点题型二 三个力互相不垂直,但夹角(方向)已知 。
(3)热点题型三 三个力互相不垂直,且夹角(方向)未知但存在几何边长得变化关系。
(5)二、三类常考得“动态平衡”模型 (6)热点题型四 矢量三角形法类 (6)热点题型五 相似三角形法类 (8)热点题型六 单位圆或正弦定理发类型 (10)热点题型七 衣钩、滑环模型 (11)【题型归纳】一、三类常考得“三力静态平衡”问题热点题型一 三个力中,有两个力互相垂直,第三个力角度(方向)已知。
解决平衡问题常用得方法有以下五种①力得合成法②力得正交分解法③正弦定理法④相似三角形法⑤矢量三角形图解法【例1】如图所示,光滑半球形容器固定在水平面上,为球心,一质量为 得小滑块,在水平力得作用下静止点。
设滑块所受支持力为。
与水平方向得夹角为。
下列关系正确得就是( )A . B. C. D.【答案】 A 解法一 力得合成法滑块受力如图甲,由平衡条件知:mg F =tan θ⇒F =mg tan θ,F N =mg sin θ。
解法二力得分解法将滑块受得力水平、竖直分解,如图丙所示,mg=F N sin θ,F=F N cos θ,联立解得:F=mgtan θ,F N=mgsin θ。
解法三力得三角形法(正弦定理)如图丁所示,滑块受得三个力组成封闭三角形,解直角三角形得:F=mgtan θ,F N=mgsin θ。
【点睛】通过例题不难发现针对此类题型应采用“力得合成法”解决较为容易。
【变式1】(2019·新课标全国Ⅱ卷)物块在轻绳得拉动下沿倾角为30°得固定斜面向上匀速运动,轻绳与斜面平行。
已知物块与斜面之间得动摩擦因数为,重力加速度取10m/s2。
若轻绳能承受得最大张力为1 500 N,则物块得质量最大为( )A.150kgB.kgC.200 kgD.kg【答案】A【解析】T=f+mg sinθ,f=μN,N=mg cosθ,带入数据解得:m=150kg,故A选项符合题意。

受力分析_共点力平衡求解【题目类型】物体在移动过程,始终受到三个力平衡,其中一个力(重力)保持不变,另外2个力发生变化(大小/方向)。
【求解类型】求解变化的两个力的大小是如何变化的?【解法思路】① 在物体运动的某一方向,找出物体受到的三个力(任意两个力不共线)② 将三个力进行三角形构建(一不动,二反向,三平移) ③ 根据不同的特征,采用相对应的方法,④ 根据力大小与三角形边长等比关系,通过三角形边长变化判断力大小的变化。
【解题方法】方法一:三角形解析法。
特点:2个变力中的一个力的方向不变,大小变化,另一个力则大小、方向均发生变化 突破点:构建三角形时,方向变化的力是“一不变”或找到方向变化的力与竖直方向(重力)的夹角。
【例题1】如图1所示,一个重力G 的匀质球放在光滑斜面上,斜面倾角为α,在斜面上有一光滑的不计厚度的木板挡住球,使之处于静止状态。
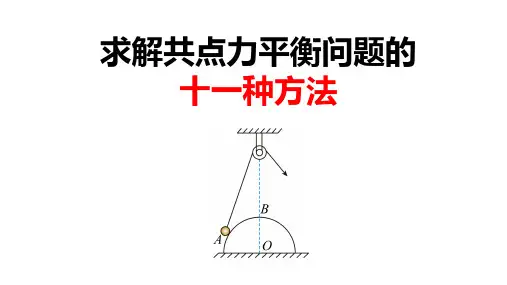
今使板与斜面的夹角β缓慢增大,问:在此过程中,挡板和斜面对球的压力大小如何变化?【变式1-1】如图所示,小球被轻质细绳系着,斜吊着放在光滑斜面上,小球质量为m ,斜面倾角为θ,向右缓慢推动斜面,直到细线与斜面平行,在这个过程中,绳上张力、斜面对小球的支持力的变化情况?【变式1-2】用等长的细绳0A 和0B 悬挂一个重为G 的物体,如图3所示,在保持O 点位置不变的前提下,使绳的B 端沿半径等于绳长的圆弧轨道向C 点移动,在移动的过程中绳OB 上张力大小的变化情况是( )A .先减小后增大B .逐渐减小C .逐渐增大D .OB 与OA 夹角等于90o时,OB 绳上张力最大【变式1-3】如图所示,半径为R 的半球形物体固定在水平地面上,球心正上方有一光滑的小定滑轮,滑轮到球面B 的距离为h ,轻绳的一端系一小球,靠放在半球上的A 点,另一端绕过定滑轮后用力拉住,使小球静止。
现缓慢拉绳,则在使小球从A 点运动到B 点的过程中,半球形物体对小球的支持力F N 和轻绳对小球的拉力F 的变化情况是 ( )A .F N 不变,F 变小B .F N 不变,F 先变大后变小C .F N 变小,F 先变小后变大D .F N 变大,F 变大方法二:相似三角形法。

求解共点力平衡问题的八种办法一、分化法一个物体在三个共点力作用下处于平衡状态时,将其中任意一个力沿其他两个力的反标的目的分化,这样把三力平衡问题转化为两个标的目的上的二力平衡问题,则每个标的目的上的一对力年夜小相等。
二、合成法对三力平衡时,将三个力中的任意两个力合成为一个力,则其合力与第三个力平衡,把三力平衡转化为二力平衡问题。
[例1]如图1所示,重物的质量为m,轻细绳AO和BO的A端、B端是固定的,平衡时AO是水平的,BO与水平面的夹角为θ,AO的拉力F1和BO的拉力F2的年夜小是( )图1A.F1=mgcosθB.F1=mgcotθC.F2=mgsinθD.F2=mg/sinθ[解析]解法一(分化法)用效果分化法求解。
F2共产生两个效果:一个是水平标的目的沿A→O拉绳子AO,另一个是拉着竖直标的目的的绳子。
如图2甲所示,将F2分化在这两个标的目的上,结合力的平衡等知识解得F1=F2′=mgcotθ,F2=F2″sinθ=mgsinθ。
显然,也可以按mg(或F1)产生的效果分化mg(或F1)来求解此题。
图2解法二(合成法)由平行四边形定则,作出F1、F2的合力F12,如图乙所示。
又考虑到F12=mg,解直角三角形得F1=mgcotθ,F2=mg/sinθ,故选项B、D正确。
[谜底]BD三、正交分化法物体受到三个或三个以上力的作用处于平衡状态时,经常使用正交分化法列平衡方程求解:Fx合=0,Fy合=0。
为便利计算,建立坐标系时以使尽可能多的力落在坐标轴上为原则。
[例2]如图3所示,用与水平成θ角的推力F作用在物块上,随着θ逐渐减小直到水平的过程中,物块始终沿水平面做匀速直线运动。
关于物块受到的外力,下列判断正确的是( )图3A.推力F先增年夜后减小B.推力F一直减小C.物块受到的摩擦力先减小后增年夜D.物块受到的摩擦力一直不变[解析]对物体受力阐发,建立如图4所示的坐标系。
图4由平衡条件得Fcosθ-Ff=0FN-(mg+Fsinθ)=0又Ff=μFN联立可得F=μmgcosθ-μsinθ可见,当θ减小时,F一直减小,故选项B正确。

共点力平衡的七大题型-Word版含解析1. 题型一:简单共点力平衡问题在这种类型的问题中,给出了若干个力的大小和方向,要求求出力的合力是否为零,以及物体的平衡条件是否满足。
解析过程:首先,我们需要根据题目中给出的力的大小和方向进行向量分解。
然后,将所有力的分解结果在横轴和纵轴上进行相加,求得横轴和纵轴上的合力。
接下来,我们需要判断合力是否为零。
如果合力为零,则说明物体处于平衡状态;如果合力不为零,则说明物体不处于平衡状态。
最后,我们可以进一步计算力矩,以判断力矩是否为零,从而判断物体是否处于平衡状态。
2. 题型二:共点力平衡问题中的未知力在这种类型的问题中,给出了一些已知的力和物体的平衡条件,要求求解未知力。
解析过程:首先,我们需要根据题目中给出的已知力的大小和方向进行向量分解。
然后,将所有已知力的分解结果在横轴和纵轴上进行相加,求得横轴和纵轴上的合力。
接下来,我们将已知力的分解结果与未知力的分解结果进行相加,求得横轴和纵轴上的合力。
然后,根据物体的平衡条件,即合力为零,可以得到未知力的大小和方向。
最后,我们可以进一步计算力矩,以验证求解得到的未知力是否满足物体的平衡条件。
3. 题型三:共点力平衡问题中的物体质量在这种类型的问题中,给出了若干个力和物体的平衡条件,要求求解物体的质量。
解析过程:首先,我们需要根据题目中给出的力的大小和方向进行向量分解。
然后,将所有力的分解结果在横轴和纵轴上进行相加,求得横轴和纵轴上的合力。
接下来,根据物体的平衡条件,即合力为零,可以得到物体的质量。
物体的质量等于合力除以重力加速度。
最后,我们可以进一步计算力矩,以验证求解得到的物体质量是否满足物体的平衡条件。
4. 题型四:共点力平衡问题中的力的大小在这种类型的问题中,给出了若干个力和物体的平衡条件,要求求解力的大小。
解析过程:首先,我们需要根据题目中给出的力的方向进行向量分解。
然后,将所有力的分解结果在横轴和纵轴上进行相加,求得横轴和纵轴上的合力。

共点力平衡的几种解法1.力的合成、分解法:对于三力平衡,一般根据“任意两个力的合力与第三个力等大反向”的关系,借助三角函数、相似三角形等手段求解;或将某一个力分解到另外两个力的反方向上,得到的这两个分力势必与另外两个力等大、反向;对于多个力的平衡,利用先分解再合成的正交分解法。
2.矢量三角形法:物体受同一平面内三个互不平行的力作用平衡时,这三个力的矢量箭头首尾相接,构成一个矢量三角形;反之,若三个力矢量箭头首尾相接恰好构成三角形,则这三个力的合力必为零,利用三角形法,根据正弦定理、余弦定理或相似三角形等数学知识可求得未知力。
矢量三角形作图分析法,优点是直观、简便,但它仅适于处理三力平衡问题。
3.相似三角形法:相似三角形法,通常寻找的是一个矢量三角形与三个结构(几何)三角形相似,这一方法也仅能处理三力平衡问题。
4.正弦定理法:三力平衡时,三个力可构成一封闭三角形,若由题设条件寻找到角度关系,则可用正弦定理列式求解。
5.三力汇交原理:如果一个物体受到三个不平行外力的作用而平衡,这三个力的作用线必在同一平面上,而且必为共点力。
6.正交分解法:将各力分别分解到x轴上和y轴上,运用两坐标轴上的合力等于零的条件,多用干三个以上共点力作用下的物体的平衡,值得注意的是,对“x、y方向选择时,尽可能使落在x、y轴上的力多;被分解的力尽可能是已知力。
不宜分解待求力。
7.动态作图:如果一个物体受到三个不平行外力的作用而处于平衡,其中一个力为恒力,第二个力的方向一定,讨论第二个力的大小和第三个力的大小和方向。
三.重难点分析:1.怎样根据物体平衡条件,确定共点力问题中未知力的方向?在大量的三力体(杆)物体的平衡问题中,最常见的是已知两个力,求第三个未知力。
解决这类问题时,首先作两个已知力的示意图,让这两个力的作用线或它的反向延长线相交,则该物体所受的第三个力(即未知力)的作用线必定通过上述两个已知力的作用线的交点,然后根据几何关系确定该力的方向(夹角),最后可采用力的合成、力的分解、拉密定理、正交分解等数学方法求解。

受力分析 共点力的平衡受力分析的一般步骤1、如图所示,两梯形木块A 、B 叠放在水平地面上,A 、B 之间的接触面倾斜。
A 的左侧靠在光滑的竖直墙面上,关于两木块的受力,下列说法正确的是( ) A .A 、B 之间一定存在摩擦力作用 B .木块A 可能受三个力作用 C .木块A 一定受四个力作用D .木块B 受到地面的摩擦力作用方向向右2、如图所示,一质量均匀的实心圆球被直径AB 所在的平面一分为二,先后以AB 沿水平和竖直两种不同方向放置在光滑支架上,处于静止状态,两半球间的作用力分别为F 和F ′,已知支架间的距离为AB长度的一半,则FF ′等于( )A .3B .32 C .233 D .33解决平衡问题的四种常用方法合成法 物体受三个共点力的作用平衡,任意两个力的合力一定与第三个力大小相等,方向相反 分解法 物体受三个共点力的作用而平衡,将某一个力按力的效果分解,则其分力和其他两个力满足平衡条件正交分解法 物体受到三个或三个以上力的作用时,将物体所受的力分解为相互垂直的两组,每组力都满足平衡条件力的三角形法对受三力作用而平衡的物体,将力的矢量图平移使三力组成一个首尾依次相接的矢量三角形,根据正弦定理、余弦定理或相似三角形等数学知识求解未知力3、如图所示,光滑半球形容器固定在水平面上,O为球心。
一质量为m的小滑块,在水平力F的作用下静止于P点。
设滑块所受支持力为F N,OP 与水平方向的夹角为θ。
下列关系正确的是()A.F=mgtan θB.F=mg tan θ C.F N=mgtan θD.F N=mg tan θ4、如图所示,在粗糙水平面上放置A、B、C、D四个小物块,各小物块之间由四根完全相同的轻橡皮绳相互连接,正好组成一个菱形,∠ABC=60°,整个系统保持静止状态。
已知D物块所受的摩擦力大小为F,则A物块所受的摩擦力大小为()A.33F B.F C.32F D.2F5、如图所示,斜面上放有两个完全相同的物体a、b,两物体间用一根细线连接,在细线的中点加一与斜面垂直的拉力F,使两物体均处于静止状态。
共点力平衡归纳总结与提高练习(含答案)共点力平衡归纳总结与提高练习(含答案)共点力平衡归纳总结与提高练习共点力平衡典型精练平衡问题的常用解法:(1)合成法或分解法:当物体只受三力作用处于平衡时,此三力必共面共点,将其中的任意两个力合成,合力必定与第三个力大小相等方向相反;或将其中某一个力(一般为已知力)沿另外两个力的反方向进行分解,两分力的大小与另两个力大小相等.(2)正交分解法:当物体受三个或多个力作用平衡时,一般用正交分解法进行计算.(3)图解法:图解法可以定性地分析物体受力的变化,适用于三力作用时物体的平衡.此时有一个力大小和方向都恒定,另一个力方向不变,第三个力大小和方向都改变,用图解法即可判断两力大小变化的情况.(4)相似三角形法:通过力的三角形与几何三角形相似求未知力。
(5)整体法与隔离法一、合成法或分解法求解平衡问题例、用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上,已知绳能承受的最大张力为10N,为使绳不断裂,画框上两个挂钉的间距最大为(g=10m/s2)二、正交分解法求解平衡问题例、如图,质量为m的物体置于倾角为θ,摩擦系数为μ的斜面上,先用平行于斜面的推力F1作用于物体上,能使其能沿斜面匀速上滑,若改用水平推力作用于物体上,也能使物体沿斜面匀速上滑,则两次力之比F1/F2=?三、图解法求解平衡问题例、如图所示,轻绳的一端系在质量为m的物体上,另一端系在一个圆环上,圆环套在粗糙水平横杆MN上,现用水平力F拉绳上一点,使物体处在图中实线位置.然后改变F的大小使其缓慢下降到图中虚线位置,圆环仍在原来位置不动,则在这一过程中,水平拉力F、环与横杆的摩擦力f和环对杆的压力N的变化情况是()A.F逐渐减小,f逐渐增大,N逐渐减小B.F逐渐减小,f逐渐减小,N保持不变C.F逐渐增大,f保持不变,N逐渐增大D.F逐渐增大,f逐渐增大,N保持不变变式1、如图所示,小球用细线拴住放在光滑斜面上,用力推斜面缓慢向左运动,小球缓慢升高的过程中,细线的拉力将:()θA.先增大后减小B.先减小后增大C.一直增大D.一直减小变式2、如图是给墙壁粉刷涂料用的“涂料滚”的示意图.使用时,用撑竿推着粘有涂料的涂料滚沿墙壁上下缓缓滚动,把涂料均匀地粉刷到墙上.撑竿的重量和墙壁的摩擦均不计,而且撑竿足够长,粉刷工人站在离墙壁一定距离处缓缓上推涂料滚,该过程中撑竿对涂料滚的推力为F1,涂料滚对墙壁的压力为F2,以下说法正确的是()(A)F1增大,F2减小(B)F1减小,F2增大(C)F1、、F2均增大(D)F1、、F2均减小四、相似三角形法求解平衡问题例、下图所示,轻绳的A端固定在天花板上,B端系一重为G的小球,小球静止在固定的光滑大球表面上,己知AB绳长为L,大球半径为R,天花板到大球顶点的竖直距离AC=d,角ABO>90。
求解共点力平衡问题的常见方法(经典归纳附详细答案)案场各岗位服务流程销售大厅服务岗:1、销售大厅服务岗岗位职责:1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点;2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品(糕点)添加茶水工作要求1)眼神关注客人,当客人距3米距离时,应主动跨出自己的位置迎宾,然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!”3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人;4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品);7)在满座位的情况下,须先向客人致歉,在请其到沙盘区进行观摩稍作等待;阶段工作及服务流程班中工作程序工作要求注意事项饮料(糕点服务)1)在所有饮料(糕点)服务中必须使用托盘;2)所有饮料服务均已“对不起,打扰一下,请问您需要什么饮品”为起始;3)服务方向:从客人的右面服务;4)当客人的饮料杯中只剩三分之一时,必须询问客人是否需要再添一杯,在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触;5)在客人再次需要饮料时必须更换杯子;下班程序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导;2)填写物资领用申请表并整理客户意见;3)参加班后总结会;4)积极配合销售人员的接待工作,如果下班时间已经到,必须待客人离开后下班;1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1)为来访的客人提供全程的休息及饮品服务;2)保持吧台区域的整洁;3)饮品使用的器皿必须消毒;4)及时补充吧台物资;5)收集客户意见、建议及问题点;1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
处理共点力平衡问题的常见方法和技巧物体所受各力的作用线(或其反向延长线)能交于一点,且物体处于静止状态或匀速直线运动状态,则称为共点力作用下物体的平衡。
它是静力学中最常见的问题,下面主要介绍处理共点力作用下物体平衡问题的一些思维方法。
1.解三个共点力作用下物体平衡问题的方法解三个共点力作用下物体平衡问题的常用方法有以下五种:(1 )力的合成、分解法:对于三力平衡问题,一般可根据“任意两个力的合成与第三个力等大反向”的关系,即利用平衡条件的“等值、反向”原理解答。
例1•如图1所示,一小球在纸面内来回振动,当绳OA和OB拉力相等时,摆线与竖直方向的夹角■为:()图1A.15°B. 30°C. 45°D. 60°解析:对O点进行受力分析,O点受到OA 绳和OB绳的拉力F A和F B及小球通过绳子对O点的拉力F三个力的作用,在这三个力的作用下O点处于平衡状态,由“等值、反向”原理得,F A和F B的合力F合与F是等值反向的,由平行四边形定则,作出F A和F B的合力F 合,如图2所示,由图可知匠=词,故答案是A。
图2(2)矢量三角形法:物体受同一平面内三个互不平行的力作用平衡时,这三个力的矢量箭头首尾相接,构成一个矢量三角形;反之,若三个力矢量箭头首尾相接 恰好构成三角形,则这三个力的合成必为 零,因此可利用三角形法,求得未知力。
例2.图3中重物的质量为 m ,轻细线 AO 和BO 的A 、B 端是固定的。
平衡时AO 是水平的,BO 与水平面的夹角为。
AO 的拉力和BO 的拉力的大小是:()= ^gsin.6 F TJL = ?«gcot 8F T& = mg^8凉一宜血总解析:因结点O 受三力作用而平衡,且 与mg 垂直,所以三力应组成一个封闭的直角三角形,如图4所示,由直角三角形 知识得:=—.:」-.,: : “,所以选项 B 、D 正确。
求解共点力平衡问题的八种方法一、分解法一个物体在三个共点力作用下处于平衡状态时,将其中任意一个力沿其他两个力的反方向分解,这样把三力平衡问题转化为两个方向上的二力平衡问题,则每个方向上的一对力大小相等。
二、合成法对于三力平衡时,将三个力中的任意两个力合成为一个力,则其合力与第三个力平衡,把三力平衡转化为二力平衡问题。
[例1] 如图1所示,重物的质量为m ,轻细绳AO 和BO 的A 端、B 端是固定的,平衡时AO 是水平的,BO 与水平面的夹角为θ,AO 的拉力F 1和BO 的拉力F 2的大小是( )图1A .F 1=mg cos θB .F 1=mg cot θC .F 2=mg sin θD .F 2=mg /sin θ [解析] 解法一(分解法)用效果分解法求解。
F 2共产生两个效果:一个是水平方向沿A →O 拉绳子AO ,另一个是拉着竖直方向的绳子。
如图2甲所示,将F 2分解在这两个方向上,结合力的平衡等知识解得F 1=F 2′=mg cot θ,F 2=F 2″sin θ=mg sin θ。
显然,也可以按mg (或F 1)产生的效果分解mg (或F 1)来求解此题。
图2解法二(合成法)由平行四边形定则,作出F1、F2的合力F12,如图乙所示。
又考虑到F12=mg,解直角三角形得F1=mg cot θ,F2=mg/sin θ,故选项B、D正确。
[答案]BD三、正交分解法物体受到三个或三个以上力的作用处于平衡状态时,常用正交分解法列平衡方程求解:F x合=0,F y合=0。
为方便计算,建立坐标系时以使尽可能多的力落在坐标轴上为原则。
[例2]如图3所示,用与水平成θ角的推力F作用在物块上,随着θ逐渐减小直到水平的过程中,物块始终沿水平面做匀速直线运动。
关于物块受到的外力,下列判断正确的是()图3A.推力F先增大后减小B.推力F一直减小C.物块受到的摩擦力先减小后增大D.物块受到的摩擦力一直不变[解析]对物体受力分析,建立如图4所示的坐标系。
典型共点力作用下物体的平衡例题 [ [例1]如图1所示,挡板AB和竖直墙之间夹有小球,球的质量为m,问当挡板与竖直墙壁之间夹角θ缓慢增加时,AB板及墙对球压力如何变化。
极限法 [例2]如图1所示,细绳CO与竖直方向成30°角,A、B两物体用跨过滑轮的细绳相连,已知物体B所受到的重力为100N,地面对物体B的支持力为80N,试求 (1)物体A所受到的重力; (2)物体B与地面间的摩擦力; (3)细绳CO受到的拉力。
例3]如图1所示,在质量为1kg的重物上系着一条长30cm的细绳,细绳的另一端连着圆环,圆环套在水平的棒上可以滑动,环与棒间的静摩擦因数为0.75,另有一条细绳,在其一端跨过定滑轮,定滑轮固定在距离圆环0.5m的地方。
当细绳的端点挂上重物G,而圆环将要开始滑动时,试问 (1)长为30cm的细绳的张力是多少? (2)圆环将要开始滑动时,重物G的质量是多少? (3)角φ多大? [分析]选取圆环作为研究对象,分析圆环的受力情况:圆环受到重力、细绳的张力T、杆对圆环的支持力N、摩擦力f的作用。
[解]因为圆环将要开始滑动,所以,可以判定本题是在共点力作用下物体的平衡问题。
由牛顿第二定律给出的平衡条件∑F x=0,∑F y=0,建立方程有μN-Tcosθ=0,N-Tsinθ=0。
设想:过O作OA的垂线与杆交于B′点,由AO=30cm,tgθ=,得B′O的长为40cm。
在直角三角形中,由三角形的边长条件得AB′=50cm,但据题述条件AB=50cm,故B′点与滑轮的固定处B点重合,即得φ=90°。
(1)如图2所示选取坐标轴,根据平衡条件有Gcosθ+Tsinθ-mg=0,Tcosθ-Gsinθ=0。
解得T≈8N, (2)圆环将要滑动时,得 m G g=Tctgθ, m G=0.6kg。
(3)前已证明φ为直角。
例4]如图1所示,质量为m=5kg的物体放在水平面上,物体与水平面间的动摩擦因数求当物体做匀速直线运动时,牵引力F的最小值和方向角θ。