人教版高中物理必修一整体法和隔离法解连接体问题练习

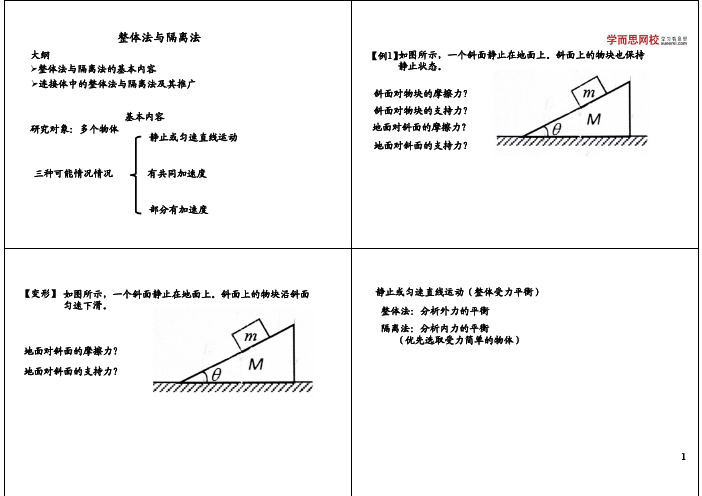
0角及F 为已知，求 A 与B 之间的压力为多少?醇静止不动，则左边木板对第一块砖，第二块砖对第三块砖的摩擦力分别为A. 4mg 、2mg B . 2mg 、0 C. 2mg mg 6 .如图所示，两个完全相同的重为G 的球，两球与水平地面间的动摩擦因市委都是球上，在绳的中点施加一个竖直向上的拉力，当绳被拉直后，两段绳间的夹角为整体法和隔离法对于连结体问题，通常用隔离法，也可采用整体法。

如果能够运用整体法，我们应该优先采用整体法，这样涉及 的研究对象少，未知量少，方程少，求解简便; 一般首先考虑整体法。

对于大多数动力学问题, 合的方法。

一、静力学中的整体与隔离 不计物体间相互作用的内力，或物体系内的物体的运动状态相同, 单纯采用整体法并不一定能解决，通常采用整体法与隔离法相结 通常在分析 外力对系统的作用时，用整体法 应遵循“先整体、后隔离” 的原则。

;在分析 系统内各物体（各部分）间相互作用时，用隔离法. 解题中1.在粗糙水平面上有一个三角形木块 a,在它的两个粗糙斜面上分别放有质量为 所示，已知 m1>m2三木块均处于静止，则粗糙地面对于三角形木块（ m1和m2的两个木块 b 和c,如图） A. B . C . D . 有摩擦力作用，摩擦力的方向水平向右 有摩擦力作用，摩擦力的方向水平向左 有摩擦力作用，但摩擦力的方向不能确定 没有摩擦力的作用 2.有一个直角支架 AOB, AO 水平放置，表面粗糙, OB 竖直向下，表面光滑， AO 上套有小环 P, OB 上套有小环 Q, 两环质量均为 mi,两环间由一根质量可忽略、不可伸展的细绳相连，并在某一位置平衡，如图。

现将 P 环向左移 一小段距离，两环再次达到平衡，那么将移动后的平衡状态和原来的平衡状态比较, AO 杆对P 环的支持力 N 和细 绳上的拉力T 的变化情况是（ A. N 不变，T 变大 B . N 不变，T 变/] C. N 变大，T 变大 D. N 变大，T 变/] 3.如图所示，设 A 重10N, B 重20N, A 、B 间的动摩擦因数为 0.1 , 为0.2 .问：（1）至少对B 向左施多大的力，才能使 A 、B 发生相对 间科1=0.4, B 与地间 科2=0.l ,则F 多大才能产生相对滑动？ B 与地面的摩擦因数 滑动？ （ 2）若A 、B 4.将长方形均匀木块锯成如图所示的三部分, 当用与木块左侧垂直的水平向右力其中日C 两部分完全对称,F 作用时，木块恰能向右匀速运动，且 现将三部分拼在一起放在粗糙水平面上，A 与B 、A 与C 均无相对滑动，图中的5.如图所示，在两块相同的竖直木板间，有质量均为 m 的四块相同的砖, 用两个大小均为 F 的水平力压木板，使科，一根轻绳两端固接在两个0 o 问当F 至少多大时，两球将D . 4mg 、mg发生滑动？7 .如图所示，重为 8N 的球静止在与水平面成 370角的光滑斜面上，并通过定滑轮与重4N 的物体A 相连，光滑挡板与水平而垂直，不计滑轮的摩擦，绳子的质量，求斜面和挡板所受的压力( sin37 0=0.6 )。

【专题概述】整体法和隔离法是牛顿第二定律应用中极为普遍的方法.隔离法是根本，但有时较烦琐；整体法较简便，但无法求解系统内物体间相互作用力.所以只有两种方法配合使用，才能有效解题.故二者不可取其轻重.连接体问题对在解题过程中选取研究对象很重要.有时以整体为研究对象，有时以单个物体为研究对象.整体作为研究对象可以将不知道的相互作用力去掉，单个物体作研究对象主要解决相互作用力.对于有共同加速度的连接体问题，一般先用整体法由牛顿第二定律求出加速度，再根据题目要求，将其中的某个物体进行隔离分析和求解．由整体法求解加速度时，F=ma，要注意质量m与研究对象对应．一、整体法、隔离法的选用1．整体法的选取原则若在已知与待求量中一涉及系统内部的相互作用时，可取整体为研究对象，分析整体受到的外力，应用牛顿第二定律列方程。

当系统内物体的加速度相同时：；否则。

2．隔离法的选取原则若在已知量或待求量中涉及到系统内物体之间的作用时，就需要把物体从系统中隔离出来，应用牛顿第二定律列方程求解．3．整体法、隔离法的交替运用若连接体内各物体具有相同的加速度，且要求物体之间的作用力时，可以先用整体法求出加速度，然后再用隔离法选取合适的研究对象，应用牛顿第二定律求作用力．即“先整体求加速度，后隔离求内力”．二、运用隔离法解题的基本步骤1.明确研究对象或过程、状态，选择隔离对象.2.将研究对象从系统中隔离出来，或将研究的某状态、某过程从运动的全过程中隔离出来.3.对隔离出的研究对象进行受力分析，注意只分析其它物体对研究对象的作用力.4.寻找未知量与已知量之间的关系，选择适当的物理规律列方程求解.【典例精析】【典例1】如图所示,一夹子夹住木块,在力 F 作用下向上提升.夹子和木块的质量分别为m、M,夹子与木块两侧间的最大静摩擦力均为f.若木块不滑动,力F的最大值是( )A BC D【典例2】如图所示,质量为M的框架放在水平地面上,一轻质弹簧上端固定在框架上,下端固定一个质量为m的小球,小球上下振动时,框架始终没有跳起,当框架对地面压力为零的瞬间,小球的加速度大小为当连体中各物体的加速度不同或涉及到各物体之间的相互作用力，要用隔离法解题，用隔离法对研究对象受力分析时，只分析它受到的力，而它对其它物体的反作用力不考虑，然后利用牛顿第二定律求解.【典例3】如图所示，猴子的质量为m，开始时停在用绳悬吊的质量为M的木杆下端，当绳子断开瞬时，猴子沿木杠以加速度a（相对地面）向上爬行，则此时木杆相对地面的加速度为（）A．g B．C．D．【典例4】倾角,质量的粗糙斜面位于水平地面上,质量的木块置于斜面顶端,从静止开始匀加速下滑,经到达底端,运动路程,在此过程中斜面保持静止取,求:(1)斜面对木块的摩擦力大小.(2)地面对斜面的支持力大小.【典例5】如图, m和M保持相对静止,一起沿倾角为的光滑斜面下滑,则M和m间的摩擦力大小是多少?【总结提升】1.整体法的选取原则若连接体内各物体具有相同的加速度，且不需要求物体之间的作用力，则可以把它们看成一个整体，分析整体受到的合外力，应用牛顿第二定律求出加速度（或其他未知量）.2.隔离法的选取原则若连接体内各物体的加速度不相同，或者需要求出系统内各物体之间的作用力，则需要把物体从系统中隔离出来，应用牛顿第二定律列方程求解。

高一物理整体法隔离法试题答案及解析1. 如图所示，在粗糙水平面上放一质量为M 的斜面体，质量为m 的木块在竖直向上力F 作用下，沿斜面体匀速下滑，此过程中斜面体保持静止，则地面对斜面（ ）A ．无摩擦力B ．有水平向左的摩擦力C ．支持力为（M+m ）gD ．支持力小于（M+m ）g【答案】AD【解析】对物体M 和m 整体受力分析，受拉力F 、重力（M+m ）g 、支持力F N ，根据共点力平衡条件竖直方向 F N +F-（M+m ）g=0，解得：F N =（M+m ）g-F ＜（M+m ）g ；水平方向不受力，故没有摩擦力． 故选AD ．【考点】整体法及隔离法。

2. 如图所示，两个等大的水平力F 分别作用在B 和C 上．A 、B 、C 都处于静止状态．各接触面与水平地面平行．A 、C 间的摩擦力大小为f 1，B 、C 间的摩擦力大小为f 2，C 与地面间的摩擦力大小为f 3，则（ ）A ．f 1=0，f 2=0，f 3=0B ．f 1=0，f 2=F ，f 3=0C ．f 1=F ，f 2=0，f 3=0D ．f 1=0，f 2=F ，f 3=F 【答案】B【解析】以ABC 整体为研究对象，分析整体在水平方向的受力易知，地面对C 的摩擦力为零，以A 为研究对象，A 处于平衡状态，故C 与A 之间无摩擦力，以B 为研究对象，易知C 与B 之间的摩擦力为F ，故选B 【考点】考查整体隔离法点评：本题难度较小，处理此类问题，研究对象的选择是灵活的，例如分析BC 间摩擦力时，可以以A 、C 整体为研究对象3. 如图水平向左的拉力F 作用在木块2上，三木块一起向左匀速运动，以下说法正确的是A ．木块1受到了向左的摩擦力B ．木块2受到了2对平衡力C ．木块1、2间有2对作用力和反作用力D ．木块2、3间有2对作用力和反作用力【答案】D【解析】三木块一起向左匀速运动，说明整体合外力为零。

将1物体隔离开，则水平方向静摩擦力为零，所以A错。

高中物理整体法隔离法解决物理试题的基本方法技巧及练习题及练习题一、整体法隔离法解决物理试题1．a、b两物体的质量分别为m1、m2，由轻质弹簧相连。

当用大小为F的恒力沿水平方向拉着 a，使a、b一起沿光滑水平桌面做匀加速直线运动时，弹簧伸长量为x1;当用恒力F竖直向上拉着 a，使a、b一起向上做匀加速直线运动时，弹簧伸长量为x2；当用恒力F倾斜向上向上拉着 a，使a、b一起沿粗糙斜面向上做匀加速直线运动时，弹簧伸长量为x3，如图所示。

则（）A．x1= x2= x3 B．x1 >x3= x2C．若m1>m2，则 x1>x3= x2 D．若m1<m2，则 x1＜x3= x2【答案】A【解析】【详解】通过整体法求出加速度，再利用隔离法求出弹簧的弹力，从而求出弹簧的伸长量。

对右图，运用整体法，由牛顿第二定律得整体的加速度为：；对b物体有：T1=m2a1；得；对中间图：运用整体法，由牛顿第二定律得，整体的加速度为：；对b物体有：T2-m2g=m2a2得：；对左图，整体的加速度：，对物体b：，解得；则T1=T2=T3，根据胡克定律可知，x1= x2= x3，故A正确，BCD错误。

故选A。

【点睛】本题考查了牛顿第二定律和胡克定律的基本运用，掌握整体法和隔离法的灵活运用．解答此题注意应用整体与隔离法，一般在用隔离法时优先从受力最少的物体开始分析，如果不能得出答案再分析其他物体．2．在如图所示的电路中，E为电源电动势，r为电源内阻，R1和R3均为定值电阻，R2为滑动变阻器．当R2的滑动触点在a端时合上开关S，此时三个电表A1、A2和V的示数分别为I1、I2和U．现将R2的滑动触点向b端移动，则三个电表示数的变化情况是A． I1增大，I2不变，U增大B． I1减小，I2增大，U减小C． I1增大，I2减小，U增大D． I1减小，I2不变，U减小【答案】B【解析】【分析】【详解】R2的滑动触点向b端移动时，R2减小，整个电路的总电阻减小，总电流增大，内电压增大，外电压减小，即电压表示数减小，R3电压增大，R1、R2并联电压减小，通过R1的电流I1减小，即A1示数减小，而总电流I增大，则流过R2的电流I2增大，即A2示数增大．故A、C、D错误，B正确．3．在如图所示的电路中，当开关S闭合后，电压表有示数，调节可变电阻R的阻值，使电压表的示数增大ΔU，则()A．可变电阻R被调到较小的阻值B．电阻R2两端的电压减小，减小量等于ΔUC．通过电阻R2的电流减小，减小量小于D．通过电阻R2的电流减小，减小量等于【答案】C【解析】【详解】A.由题意知，要使电压表的示数增大，则需电阻R和R1并联后的总电阻增大，则需将可变电阻R增大，即可变电阻R被调到较大的阻值，故A项不合题意；BCD.当R增大时，外电阻增大，干路电流减小，电阻R2两端的电压减小，且路端电压增大，所以电阻R2两端的电压减小量小于ΔU，由欧姆定律知，通过电阻R2的电流也减小，减小量小于，故B项不合题意、D项不合题意，C项符合题意．4．如图所示的电路中，电源电动势为E．内阻为R，L1和L2为相同的灯泡，每个灯泡的电阻和定值电阻阻值均为R．电压表为理想电表，K为单刀双掷开关，当开关由1位置掷到2位置时，下列说法中正确的是（）A．L1亮度不变，L2将变暗B．L1将变亮，L2将变暗C．电源内阻的发热功率将变小D．电压表示数将变小【答案】D【解析】开关在位置1时，外电路总电阻R总=，电压表示数U=E=，同理，两灯电压U1=U2=E，电源内阻的发热功率为P热==。

第四章运动和力的关系专题强化训练四：连接体问题和整体和隔离法的应用一、动力学的连接体问题1．连接体：两个或两个以上相互作用的物体组成的具有相同运动状态的整体叫连接体．如几个物体叠放在一起，或并排挤放在一起，或用绳子、细杆等连在一起，如图1所示，在求解连接体问题时常用的方法为整体法与隔离法．图12．整体法：把整个连接体系统看作一个研究对象，分析整体所受的外力，运用牛顿第二定律列方程求解．其优点在于它不涉及系统内各物体之间的相互作用力．3．隔离法：把系统中某一物体(或一部分)隔离出来作为一个单独的研究对象，进行受力分析，列方程求解．其优点在于将系统内物体间相互作用的内力转化为研究对象所受的外力，容易看清单个物体(或一部分)的受力情况或单个过程的运动情形．4．整体法与隔离法的选用(1)求解各部分加速度都相同的连接体问题时，要优先考虑整体法；如果还需要求物体之间的作用力，再用隔离法．(2)求解连接体问题时，随着研究对象的转移，往往两种方法交替运用．一般的思路是先用其中一种方法求加速度，再用另一种方法求物体间的作用力或系统所受合力．5.常见连接体的类型(1)同速连接体(如图)特点：两物体通过弹力、摩擦力作用，具有相同速度和相同加速度.处理方法：用整体法求出a与F合的关系，用隔离法求出F内力与a的关系.(2)关联速度连接体(如图)特点：两连接物体的速度、加速度大小相等，方向不同，但有所关联. 处理方法：分别对两物体隔离分析，应用牛顿第二定律进行求解.题型一：整体法和隔离法解决连接体问题1．（2021·重庆市渝北中学校高一月考）质量为2m 的物体A 和质量为m 的物体B 相互接触放在水平面上，如图所示，若对A 施加水平推力F ，使两物体沿水平方向做匀加速直线运动，下列说法正确的是（ ）A ．若水平面光滑，则物体A 的加速度为2F m B ．若水平面光滑，则物体A 对B 的作用力为23F C ．若水平面光滑，则物体A 对B 的作用力为13F D ．若物体A 、B 与地面的动摩擦因数均为μ，则物体A 对B 的作用力为3F mg μ- 2．（2021·云南·宣威市第十中学高一月考）如图所示，两物块置于水平地面上，其质量分别为3m 、2m ，两者之间用水平轻绳连接。

重点：整体法与隔离法的多次交替使用。

难点：解决连接体问题的关键——物体间相互作用力的求解。

利用整体法与隔离法求解动力学中的连接体问题 1. 整体法的选取原则若连接体内各物体具有相同的加速度，且不需要求物体之间的作用力，可以把它们看成一个整体，分析整体受到的合外力，应用牛顿第二定律求出加速度（或其他未知量）。

2. 隔离法的选取原则若连接体内各物体的加速度不相同，或者要求出系统内各物体之间的作用力时，就需要把物体从系统中隔离出来，应用牛顿第二定律列方程求解。

【技巧点拨】整体法、隔离法的交替运用若连接体内各物体具有相同的加速度，且要求物体之间的作用力时，可以先用整体法求出加速度，然后再用隔离法选取合适的研究对象，应用牛顿第二定律求作用力，即“先整体求加速度，后隔离求内力”。

例题1 （江苏高考）如图所示，一夹子夹住木块，在力F 作用下向上提升。

夹子和木块的质量分别为m 、M ，夹子与木块两侧间的最大静摩擦力均为f ，若木块不滑动，则力F 的最大值是（ ）A. M M m f )(2+B.m M m f )(2+C. MM m f )(2+－（m ＋M ）gD. mM m f )(2+＋（m ＋M ）g思路分析：由题意知，当M 恰好不能脱离夹子时，M 受到的摩擦力最大，F 取最大值，设此时提升的加速度为a ，由牛顿第二定律得对M 有：2f －Mg ＝Ma① 对m 有：F －2f －mg ＝ma②联立①②两式解得F ＝Mm M f )(2+，选项A 正确。

答案：A例题2 如图甲所示，质量为M 的小车放在光滑的水平面上，小车上用细线悬吊一质量为m 的小球，M ＞m 。

现用一力F 水平向右拉小球，使小球和车一起以加速度a 向右运动时，细线与竖直方向成α角，细线的拉力为T ；如图乙所示，若用一力F ′水平向左拉小车，使小球和车一起以加速度a ′向左运动时，细线与竖直方向也成α角，细线的拉力为T ′。

则（ ）A. a ′＝a ，T ′＝TB. a ′＞a ，T ′＝TC. a ′＜a ，T ′＝TD. a ′＞a ，T ′＞T思路分析：对图甲整体分析，由牛顿第二定律得a ＝mM F+，对小球受力分析如图（a ）所示，因此有F －T sin α＝ma ，T cos α＝mg ；对图乙小球受力分析如图（b ）所示，因此有T ′sin α＝ma ′，T ′cos α＝mg ，解得T ′＝T ＝αcos mg ，a ＝Mmg tan α，a ′＝g tan α，由于M ＞m ，故a ′＞a 。

专题--连接体问题（基本方法：整体法与隔离法）一、连接体：当两个或两个以上的物体通过绳、杆、弹簧相连，或多个物体直接叠放在一起的系统 二、处理方法——整体法与隔离法系统运动状态相同整体法问题不涉及物体间的内力 使用原则隔离法三、连接体题型：1【例1】A 、B 平力N F A 6=推A ，用水平力N F B 3=拉B ，A 、B【练1】如图所示，质量为M 的斜面A 在水平向左的推力F 作用下，A 与B 物体B 的质量为m ，则它们的加速度a A. ()(,sin μθ++==g m M F g a B. θθcos )(,cos g m M F g a +==C. ()(,tan μθ++==g m M F g a D. g m M F g a )(,cot +==μθ【练2】如图所示，质量为2m 的物体2滑定滑轮连接质量为1m 的物体，与物体1A. 车厢的加速度为θsin gB. 绳对物体1的拉力为θcos 1gmC. 底板对物体2的支持力为g m m )(12-D. 物体2所受底板的摩擦力为θtan 2g m2、连接体整体内部各部分有不同的加速度：【例2有一个环，箱和杆的总质量为M ，环的质量为m 加速度大小为a 时（a ＜g A. Mg + mg B. Mg —【练3】如图所示，一只质量为m 杆下降的加速度为（ ）A. gB. g M mC. g M m M +【练4个重4 N 的读数是（ ）A.4 NB.23 NC.0 N【练5】如图所示，A 、B 的质量分别为m A =0.2kg ，m B =0.4kg ，盘C 的质量m C =0.6kg ，现悬挂于天花板O 处，处于静止状态。

当用火柴烧断O 处的细线瞬间，木块A 的加速度a A 多大？木块B 对盘C 的压力F BC 多大？（g 取10m/s 2）连接体作业1、如图所示，小车质量均为M ，光滑小球P 的质量为m ，绳的质量不计，水平地面光滑。

题型一 整体法与隔离法的应用例题1 如下图，光滑水平面上放置质量分别为m 和2m 的四个木块，其中两个质量为m 的木块间用一不可伸长的轻绳相连，木块间的最大静摩擦力是μmg 。

现用水平拉力F 拉其中一个质量为2 m 的木块，使四个木块以同一加速度运动，那么轻绳对m 的最大拉力为 A 、5m g 3μ B 、4m g 3μ C 、2m g3μ D 、mg 3μ 变式1 如下图的三个物体A 、B 、C ，其质量分别为m 1、m 2、m 3，带有滑轮的物体B 放在光滑平面上，滑轮和所有接触面间的摩擦及绳子的质量均不计．为使三物体间无相对运动，那么水平推力的大小应为F ＝__________2.如图，质量为2m 的物块A 与水平地面的摩擦可忽略不计，质量为m 的物块B 与地面的动摩擦因数为μ，在水平推力F 的作用下，A 、B 做加速运动，A 对B 的作用力为多少？3.如下图，质量为M 的木箱放在水平面上，木箱中的立杆上套着一个质量为m 的小球，开场时小球在杆的顶端，由静止释放后，小球沿杆下滑的加速度为a =21g ,那么小球在下滑的过程中，木箱对地面的压力为多少？4.两个质量一样的小球用不可伸长的细线连结，置于场强为E 的匀强电场中，小球1和小球2均带正电，电量分别为q 1和q 2〔q 1＞q 2〕。

将细线拉直并使之与电场方向平行，如下图。

假设将两小球同时从静止状态释放，那么释放后细线中的张力T 为F m m 212-图B A〔不计重力及两小球间的库仑力〕〔 〕A ．121()2T q q E =-B ．12()T q q E =-C ．121()2T q q E =+D ．12()T q qE =+ 5.如下图，光滑水平面上放置质量分别为m 、2m 和3m 的三个木块，其中质量为2m 和3m 的木块间用一不可伸长的轻绳相连，轻绳能承受的最大拉力为F T 。

现用水平拉力F 拉质量为3m 的木块，使三个木块以同一加速度运动，那么以下说法正确的选项是〔 〕A ．质量为2m 的木块受到四个力的作用B ．当F 逐渐增大到F T 时，轻绳刚好被拉断C ．当F 逐渐增大到T 时，轻绳还不会被拉断D ．轻绳刚要被拉断时，质量为m 和2m 的木块间的摩擦力为13F T 题型二 通过摩擦力的连接体问题例题2 如下图，在高出水平地面h = 的光滑平台上放置一质量M = 2kg 、由两种不同材料连成一体的薄板A ，其右段长度l 2 = 且外表光滑，左段外表粗糙。

《整体法与隔离法》专题练习1、连接体：两个或两个以上的物体相互连接参加运动的系统2、整体法：当系统中各物体的加速度相同时，我们把整个系统内的所有物体看成一个整体，这个整体的质量等于各物体的质量之和，当整体受到的外力已知时，可由牛顿第二定律列方程求出整体的加速度，这种处理问题的思维方法叫做整体法。

注意：此方法一般适用于系统中各部分物体的加速度大小、方向相同的情况3、隔离法：求系统内物体间相互作用的内力时，常把某个物体从系统中“隔离”出来，作为一个单独的研究对象进行受力分析，依据牛顿第二定律列方程，这种处理连接体问题的思维方法叫隔离法注意：此方法对于系统中各部分物体的加速度大小、方向相同或不相同的情况均适用。

4、整体法和隔离法的选择求各部分的加速度相同的连接体的加速度或合外力时，优先考虑整体法；如果还要求各部分间的作用力，则用隔离法，要求哪个面上的作用力，就从哪个作用面将物体进行隔离；如果连接体中各部分加速度不同，一般都是选用隔离法。

处理连接体问题，整体法与隔离法往往交叉使用，一般的思路是先用整体法求加速度，再用隔离法求物体间的作用力。

例1、如图：两个质量相同的物体1和2紧靠在一起，放在光滑的水平桌面上，如果它们分别受到水平推力F1和F2作用，而且F1＞F2，则1对2 的作用力的大小为：例2、两物体A和B，质量分别为m1和m2，互相接触放在光滑的水平面上，如图所示，对物体A施以水平方向的力F，则A物体对B物体的作用力大小是___________,若水平面不光滑，摩擦系数为μ，A物体对B物体的作用力大小是__________例3、如图所示：质量为２ｍ的物体Ａ与水平地面的摩擦可忽略不计，质量为ｍ的物体Ｂ与地面的动摩擦因数为μ，，在已知水平力Ｆ的作用下，Ａ、Ｂ一起做加速运动，Ａ对Ｂ的作用力为：_____例4、如图：四个相同的木块并排放在光滑水平地面上，当用力F推1使它们一起加速运动时，第木块1对木块2的作用力大小是_______,木块3对木块4的作用力大小是________例5、如图，在光滑的地面上，水平外力F拉动小车和木块一起向右做匀加速运动，小车质量为M，木块质量是m，设加速度大小为a，木块和小车之间的动摩擦因数为μ，则在这个过程中，木块受到的摩擦力大小为：A、μmgB、maC、ｍＦ／（Ｍ＋ｍ）Ｄ．Ｆ－Ｍａ例6：如图所示，两个物体ｍＡ＝２ｍＢ(A在上方)，用细绳连接后放在光滑的斜面上，在它们一起下滑的过程中：（）Ａ。