常见的几何图形分割

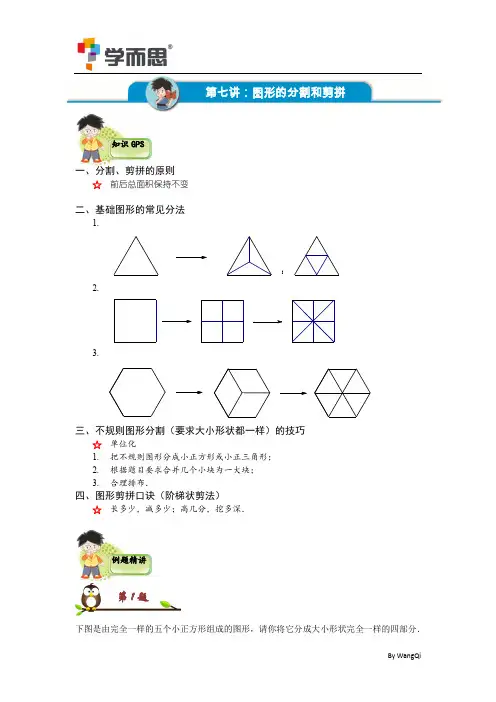
一、分割、剪拼的原则☆ 前后总面积保持不变二、基础图形的常见分法1.2.3.三、不规则图形分割（要求大小形状都一样）的技巧☆ 单位化1. 把不规则图形分成小正方形或小正三角形；2. 根据题目要求合并几个小块为一大块；3. 合理排布． 四、图形剪拼口诀（阶梯状剪法）☆ 长多少，减多少；高几分，挖多深．下图是由完全一样的五个小正方形组成的图形，请你将它分成大小形状完全一样的四部分．;第1题 例题精讲知识GPS解析：图形不规则，尝试先分成小正方形，直到分到5的倍数块，如下图一共20个小正方形，每4块合并成一大块，进行合理排布可以得到将一个49⨯的长方形剪成两部分，再拼成一个正方形．解析：直着剪，发现毫无头绪，那么就阶梯状剪．要知道我们最后要完成的目标是什么．根据剪拼前后总面积不变：4966⨯=⨯，长是9变为6，横着剪掉3格：第2题宽是4变为6，竖着剪掉2格上台阶就可以拼成下图第3题介绍一种别致的正六边形分完全相同4份的方法．当我们把图形分成很小的单元后，会找到一些新的分法，伙伴们可以多多尝试，培养对图形的感知力．比较图中两个阴影部分①和②的面积，他们的大小关系是什么？① ②解析：这道题是一道杯赛原题，它用到了面积割补的办法，也将会是寒假班“格点与割补”一讲学习的内容．① 的面积133=⨯=② 的面积3223=⨯÷=它们的面积相等。

第4题杯赛展示不得不说，这一讲的内容杯赛不会直接考，但分割图形的技巧，尤其是“面积不变”的原则对于我们高年级的几何问题来说至关重要，几乎每一道几何难题都会跟面积联系起来，也需要我们去分割．。

17五年级图形的分割练习题图形分割是数学中的一个重要概念，在五年级的学习中也占有一定的比重。

通过图形分割的练习，可以提高孩子们对几何图形的理解和应用能力。

下面我将为大家提供一些有趣的练习题，帮助五年级的学生们巩固和提高他们的图形分割能力。

练习题1：三角形的分割问题：将下面的等边三角形分割为4块相等的三角形。

（插入等边三角形的图示）解答：（插入三角形分割答案图示）练习题2：矩形的分割问题：将下面的矩形分割为4块相等的矩形。

（插入矩形图示）解答：（插入矩形分割答案图示）练习题3：正方形的分割问题：将下面的正方形分割为8块相等的小正方形。

（插入正方形图示）解答：（插入正方形分割答案图示）练习题4：圆形的分割问题：将下面的圆形分割为6块相等的扇形。

（插入圆形图示）解答：（插入圆形分割答案图示）通过以上练习题，我们可以看到图形分割有很多种不同的方式。

要想准确进行图形的分割，需要掌握一些基本的原则。

首先，分割后的图形块应当保持相等。

这意味着我们需要仔细计算每个图形块的边长或角度。

其次，分割线应当与图形的边界相切或穿过顶点。

这样才能确保分割后的图形块是连续的。

最后，我们还可以尝试不同的分割方式，发展出自己独特的解题思路。

不同的方法可以激发创造力，增强解决问题的能力。

通过反复练习图形的分割练习题，五年级的学生们将逐渐熟悉各种图形的特点，掌握图形分割的技巧，为更高级别的几何学习打下坚实的基础。

总结：图形分割是五年级数学学习中的重要内容之一。

通过分割图形的练习题，学生们可以提高对各种几何图形的理解和分析能力。

掌握图形分割的技巧，能够激发学生们的创造力和解决问题的能力。

希望以上的练习题对学生们的学习有所帮助，提升他们的图形分割能力。

几何面积问题除了利用常规的五大模型、各种公式求得之外，还可以用图形分割的思想来做。

我们发现，在迎春杯几何问题中，这类题目很多。

掌握好这种思想方法，可以帮助我们解决很多几何难题。

解题关键：分割其实就是运用特殊的三角形（等角直角三角形、等边三角形等）、正方形、等边图形的特殊性质进行分割而得，所以分割的关键是利用了特殊图形的关系解题。

解题思想：这其实就是一种化整为零的思想，各位同学不仅要学会几何题中的这种方法，更要细细体味这种思想在解决各种问题中的妙用。

模块一、简单分割【例 1】 3个相同的正方形纸片按相同的方向叠放在一起(如图)，顶点A 和B 分别与正方形中心点重合，如果所构成图形的周长是48厘米，那么这个图形覆盖的面积是__________平方厘米.【考点】图形的分割 【难度】2星 【题型】填空 【关键词】迎春杯，中年级组，复试，4题【解析】 将这3个正方形分割，可知这个图形的周长即为两个正方形纸片的周长之和，故正方形边长为48÷8=6（厘米），则图中每个分割得到的小正方形边长为6÷2=3（厘米），所以这个图形覆盖的面积为6×6×2+3×3×2=90（平方厘米）。

【答案】90平方厘米【例 2】 正方形ABCD 的面积是1平方米，将四条边分别向两端各延长一倍，连结八个端点得到一个正方形(如图)，求大正方形的面积．DCB A【考点】图形的分割 【难度】2星 【题型】解答【解析】 四条边分别向两端各延长一倍，很容易可以观察出，大正方形有9个小正方形组成，所以，大正方形的面积是：199⨯=(平方米)．【答案】9平方米例题精讲知识点拨4-2-4.图形的分割【例 3】 将边长为a 的正方形各边的中点连结成第二个正方形，再将第二个正方形各边的中点连结成第三个正方形，依此规律，继续下去，得到下图那么，边长为a 的正方形面积是图中阴影部分面积的________ 倍.【考点】图形的分割 【难度】3星 【题型】填空 【关键词】希望杯，四年级，复赛，第6题，4分 【解析】 阴影部分是大正方形的0.5×0.5×0.5×0.5=116，所以正方形是阴影的16倍 【答案】16倍【例 4】 正三角形ABC 的面积是1平方米，将三条边分别向两端各延长一倍，连结六个端点得到一个六边形(如右图)，求六边形的面积．CBA【考点】图形的分割 【难度】3星 【题型】解答【解析】 采用分割法，过A 、B 、C 分别作平行线，得到右上图，其中所有小三角形的面积都相同，所以六边形面积等于13平方米．【答案】13平方米【例 5】 正六边形ABCDEF 的面积是1平方米，将六条边分别向两端各延长一倍，交于六个点，组成如下图的图形，求这个图形的面积．FED CB A FAB CDE【考点】图形的分割 【难度】3星 【题型】解答【解析】 采用分割法，连接正六边形的对角线，会发现，所有的三角形面积都相同，一共有12个小三角形，原来正六边形的面积是1平方米，由6个小三角形组成，所以现在的大图形的面积是：122⨯= (平方米)【答案】2平方米【例 6】 长方形ABCD 的面积是40平方厘米，E 、F 、G 、H 分别为AC 、AH 、DH 、BC 的中点。

理解立体几何图形的切割立体几何图形在我们的日常生活中随处可见，从一杯咖啡的杯子到一幢高楼大厦的外形，都可以被视为立体几何图形。

而对于立体几何图形的切割也是一个非常重要的概念。

理解了立体几何图形的切割，有助于我们更好地理解它们的性质和特点。

本文将重点探讨立体几何图形的切割以及其应用。

一、切割的定义与原理切割是指将一个立体几何图形分割成两个或多个较小的部分的过程。

常见的切割方法有切块和切面两种。

切块是指将立体几何图形分割成数个立方体或其他几何形状的块状部分。

切面是指将立体几何图形通过一个平面分割成两个或多个平面图形。

在进行切割时，需要考虑到切割的方向、位置以及切割前后的图形性质等因素。

二、立体几何图形的切割应用1. 工程建设在工程建设中，立体几何图形的切割应用非常广泛。

比如在建造一座大楼时，可以通过切割立体图形来确定每层的平面图形，从而更好地进行施工规划。

又或者在制造一件复杂的零件时，通过将立体图形进行切割，可以使得制造过程更加简化和高效。

2. 数学教育立体几何的切割也是数学教育中的重要内容之一。

通过切割，学生可以更加直观地理解立体几何图形的性质和特点。

同时，通过进行切割实验，学生还可以通过观察切割后图形的变化，进一步探究立体几何的基本概念。

3. 艺术设计立体几何的切割在艺术设计中起到了重要的作用。

通过切割，可以将原本单一的立体几何图形转化为多个不同形状的图形，从而为艺术家提供更多的设计灵感。

许多艺术品的独特之处正是来源于艺术家对立体几何图形进行切割的巧妙运用。

三、立体几何图形切割的案例1. 瓦楞纸板的制作瓦楞纸板是一种常见的包装材料，其制作过程就是通过切割纸板的方式得到的。

通过对纸板进行切割，可以使得纸板具有更好的柔韧性和强度，提高其抗压能力，从而更好地满足包装需求。

2. 建筑模型的制作建筑模型的制作通常也需要对立体几何图形进行切割。

通过对模型材料进行切割，可以更好地还原建筑物的外观和内部结构。

同时，通过切割也可以使得建筑模型更加易于展示和拆卸。

长方形大小一样的四种分法
长方形是一种常见的几何图形，它在我们的日常生活中无处不在。

而对于一个大小相同的长方形，有许多种不同的分法，下面我们将介绍其中四种。

1. 水平分割
将长方形水平分割成两个部分，每个部分的高度相同，但长度可以不同。

这种分法可以有很多不同的应用，比如制作双层蛋糕、制作书籍的封面等等。

2. 竖直分割
将长方形竖直分割成两个部分，每个部分的长度相同，但高度可以不同。

这种分法也可以应用于许多场景，比如准备制作门牌、制作横幅等等。

3. 对角线分割
将长方形对角线分割成两部分，每个部分的长度和高度不同，但它们之间的比例相同。

这种分法可以应用于许多场景，比如制作方案图、制作标志等等。

4. 水平和竖直分割
将长方形同时进行水平和竖直分割，分割成四个部分，每个部分的长度和高度都不同。

这种分法可以应用于许多场景，比如制作九宫格、制作生日蛋糕等等。

总结
以上是四种将大小相同的长方形进行分割的方式。

这些分割方法可以应用于许多不同的场景中，从而实现我们想要的效果，并有效地传达我们的信息。

我们可以根据需要来选择最合适的分割方式。

小学数学几何中的割补法和分割法
割补法和分割法都是计算平面几何图形面积的推导方法，也是一种思考方法。

在面积和体积教学中，都有着广泛的应用。

割补法是指：把一个图形的某一部分割下来，填补在图形的另一部分，在原来面积不变的情况下，使其转化为已经掌握的旧的图形，以利于计算公式的推导。

平行四边形通过割补可转化为长方形（或正方形），梯形通过割补可转化为平行四边形，圆通过割补可转化为近似长方形等。

（1）平行四边形割补后转化为长方形。

（2）梯形割补后转化为平行四边形。

分割法是指：对一些不规则图形的面积，不能使用割补法，可以利用不规则图形的凹凸特点，将其分割成若干个可以计算的规则图形（如：长方形、三角形、梯形、……），先将各个规则图形的面积计算出来，然后再把这些规则图形的面积加在一起，总面积就是不规则图形的面积。

这种计算不规则图形的方法，叫做分割法。

初中数学什么是切割
在数学中，切割是指将一个图形或物体分割成若干个部分的过程。

切割可以是平面的，也可以是立体的，常见的切割方式有直线切割和曲线切割。

下面我将详细介绍切割的概念、方法和应用：
1. 直线切割：
直线切割是指通过直线将一个图形或物体分割成若干个部分。

直线切割可以是平行切割和垂直切割两种形式。

-平行切割：通过平行线将图形或物体分割成平行的多个部分。

平行切割可以用于分割长方形、正方形等图形。

-垂直切割：通过垂直线将图形或物体分割成垂直的多个部分。

垂直切割可以用于分割三角形、梯形等图形。

2. 曲线切割：
曲线切割是指通过曲线将一个图形或物体分割成若干个部分。

曲线切割可以是任意曲线，如圆弧、抛物线等。

曲线切割常见的应用场景包括分割圆形、椭圆形等图形。

3. 切割的方法：
切割可以通过直线和曲线的组合来实现。

切割的方法可以根据具体的图形和要求来选择，常用的方法包括划线、切割工具等。

4. 切割的应用：
切割在几何学和图形处理中有广泛的应用，常见的应用包括：
-分割图形：切割可以将一个图形分割成若干个部分，便于研究和分析图形的性质和特征。

-制作模型：切割可以用于制作各种模型，如纸艺、拼图等，通过切割可以将平面图形转化为立体模型。

-制作拼图：切割可以用于制作各种拼图游戏，通过切割将图形分割成若干个小块，让人们通过拼接还原原始图形。

以上是关于切割的概念、方法和应用的介绍。

切割是数学中的重要概念，它可以帮助我们更好地理解和应用图形的分割和处理技术。

希望以上内容能够满足你对切割的了解。

分形几何有许多典型的范例，以下是其中一些：
1. 谢尔宾斯基三角形：这是一种自相似的分形图形，通过不断将三角形划分为更小的三角形，最终得到具有无限复杂性的图形。

2. 谢尔宾斯基垫片：这是由谢尔宾斯基三角形进一步演化而来的一种分形图形，由三角形内部的三角形构成，整体呈现出一个自相似的模式。

3. 科赫曲线：又称为科赫雪花或科赫蛇，是一种分形曲线。

通过不断将一段线段分割成等长的两段，然后将每一段线段的中间部分弯曲成等边三角形，最终得到具有无限复杂性的图形。

4. 曼德布罗集：这是由数学家本华·曼德布罗提出的分形图形，通过不断将单位正方形进行切割和填充，最终得到的图形是一个具有无限复杂性的集合。

5. 皮亚诺曲线：这是一种由意大利数学家皮亚诺提出的分形图形，它是一种在平面上的连续曲线，通过不断将线段进行延长和弯曲，最终得到的图形具有无限复杂性和自相似性。

这些只是分形几何中的一些典型范例，实际上还有许多其他的分形图形和结构，如朱利亚集、费根堡姆曲线等。

这些分形图形的特点是具有无限的复杂性和自相似性，并且在许多领域中得到了应用。

分割图形是几何学中一个非常有趣味的课题，研究图形的分割问题不仅可以增强对几何图形的直观感受和判断能力，丰富对图形的想象力，提高数学思维能力，而且还有一定的实用价值.一、将正方形分割成若干个小正方形1926年前苏联数学家鲁金对“完美正方形”的存在提出了猜想.所谓“完美正方形”，是指它可以分割成一些边数各不相等且边长为整数的正方形.分割成小正方形的个数称为它的阶.1936年这个问题引起了英国剑桥大学三一学院的四个学生塔特、斯通、布鲁克斯、史密斯的兴趣.他们当时考虑了这样一个问题：把一个矩形分割成边长各不相等的正方形.值的说明的是,当时人们已经知道长为33、宽为32的矩形可以作正方形分割，如图1.斯通从一开始就怀疑“完美正方形”的存在，然而无法证实自己的想法；而其余三人则致力于寻找一个实际存在的“完美正方形”，但是几经失败后也开始倾向于斯通的看法.图1就在一筹莫展之际，柏林的施柏拉格居然找到了一个真实存在的“完美正方形”.这无疑是对塔特、斯通等人的一记闷棍，然而他们并没有气馁，很快改变了自己的研究方向.在理论的指导下，在1938年终于找到了一个由39个不同整数边的正方形组成的大正方形，被称为“39阶完美正方形”，如图2.这一成果大大增强了他们继续研究的信心，通过研究，发现了宽为176、长为177的矩形可分为边长不等的11个长方形（如图3）.光阴流逝，一晃过去了几十年，当年的大学生都成了蜚声数坛的组合数学专家和图论专家，他们的研究成果被成功地运用到电子、化学、建筑学、运筹学、通讯学和计算机等多个领域，成为造福人类的有力工具.图2图3数贝拾海601964年，塔特的学生威尔逊博士找到了一个25阶的完美正方形，后来这个图形保持了12年的最佳记录，直到威尔科克斯所创造的24阶完美正方形（如图4）.图41978年荷兰数学家特温特技术大学的杜依维斯廷，用大型电子计算机找出了一个21阶的完美正方形（如图5）.1962年荷兰数学家丢伐斯丁证明了小于或等于19阶的完美正方形不存在；1978年他又证明了20阶的完美正方形不存在，因而可以断定：21阶完美正方形是最小阶“完美正方形”，这个结论也同时被前苏联数学家鲁奎所证明.图5那么如何将矩形分割为边数各不相等且边长为整数的正方形呢？办法是先作一个草图，然后用尽可能少的未知数标出每个正方形的边长，再写出这些边长应满足的关系式，最后再求解这个方程组.图6如图6，先设相邻三个正方形的边长分别为x、y、z，然后按下列顺序求出其余正方形的边长：x+y、2x+y、y-z、y-2x、y-3z、2y-5z.由矩形对边相等的性质，可得出(2y-5z)+(y-2x)+(y-z)=(2x+y)+(x+y)，（2x+y)+(2y-5z)=(x+y)+y＋(y-z)3x-2y+8z=0,x-4z=0.令z=1，得x=4，y=10.这样便求得矩形被分割后的三个正方形的边长.下面我们再来看177×176的矩形是怎样分割成边数各不相等且边长为整数的正方形的.如图7，用两个未知数x，y表示所有正方形的边长，由矩形的水平边长相等得，(9x-5y)+(-2y)=(2x+5y)+(x+2y)+(x+y)+(2x+y)，即9x-16y=0，解得x=16、y=9，于是得到177×176矩形被分割后的正方形的边长.图71992年，布卡姆和杜伊维斯廷给出了21-28阶全部207个完美正方形：截至2018年，已经知道的21-35阶完美正方形的个数为：1，8，12，30，172，541，1372，3949，10209，26234，71892，196357，528866，1420439，3784262.二、将正方形分割成若干个直角三角形将一个正方形分割成若干个边长不相等的直角三角形，且使正方形的边长尽可能小，分割后的直角三角形数目也尽可能地少.这一问题最早由日本的铃木昭雄提出.至今虽然取得一些进展，但似乎看不见最终的结论.1966年，有人将一个边长为39780的大正方形分割若干个三角形；在以后的15年内，人们找到了20种数贝拾海61将边长在1000以下的正方形分割为三角形的方式.1968年，有人将边长为1248的正方形分割为5个直角三角形，如图8.1976年，有人将边长为48的正方形分割为7个直角三角形，如图9.以上分别是分割的直角三角形数最少和大正方形边长最小的，迄今为止的最好纪录.图8图9三、将正方形分割成若干个锐角三角形将一个正方形分割成若干个锐角三角形，要求分割的锐角三角形的个数尽可能少（虽不要求边长为整数）也是让人感兴趣的问题.如图10、图11、图12、图13分别是将正方形分割成11个、10个、9个、8个锐角三角形的图形，将正方形分割成8个锐角三角形是一种巧妙的方法，要想再减少锐角三角形的个数是不可能的.有趣的是，人们证明了如下事实：用边长分别为1、2、3……的正方形去覆盖平面，至少可以铺满整个平面的四分之三；还有人已经证明：要用边长大小不等的小正方体去填满一个大正方体是不可能的，亦即完美正方体是不存在的.图10图11图12图13四、分割其他图形如果把三角形、平行四边形分割成大小完全不同的正三角形，人们发现这种分割方式是不存在的.如果降低某些要求，比如允许某些正三角形边长相等，则可以找到这种分割方式.可将一个平行四边形分割成13个小正三角形（据称这是最小阶数的分割），如图14；可将一个正三角形分割成15个小正三角形，如图15.如果把正三角形记为“+”，把倒三角形记为“-”，在某种意义下，这种分割方式是完美的，那么图14、图15都可视为是完美分割图形.图14图15至此，数学家们的研究并没有停止，他们还将完美分割图形的问题推广到莫比乌斯带、圆柱面、环面和克莱因瓶上，也取得了许多有趣的成果.数贝拾海62。