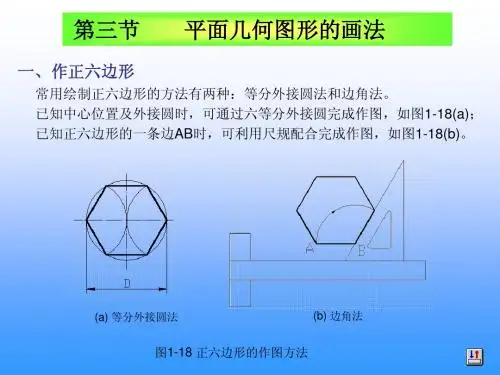
平面几何图形的画法

第5章绘制平面图形平面图形是由若干线段（直线或圆弧）封闭连接组合而成。

各组成线段之间可能彼此相交、相切或等距。

要用AutoCAD正确、快速地绘制一个平面图形，特别是较复杂的平面图形，必须首先对平面图形作尺寸分析和线段分析，然后按适当的方法、步骤画出。

与手工绘制平面图形相比，用AutoCAD绘制平面图形需要较高的作图技巧，要用到一些特殊的命令和一些特别的作图方法。

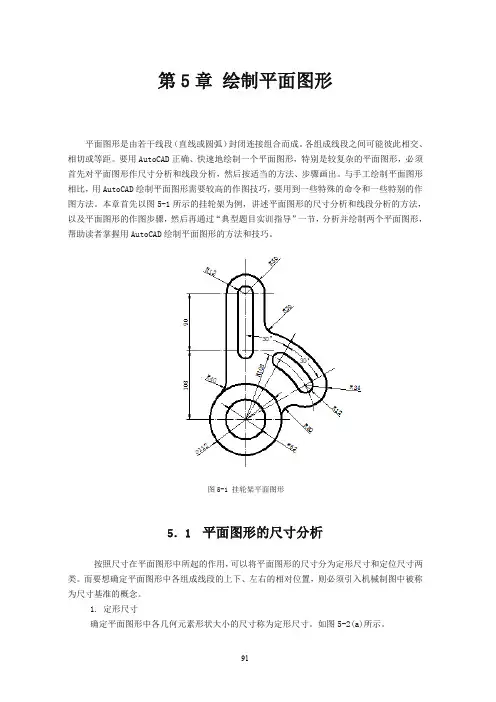
本章首先以图5-1所示的挂轮架为例，讲述平面图形的尺寸分析和线段分析的方法，以及平面图形的作图步骤，然后再通过“典型题目实训指导”一节，分析并绘制两个平面图形，帮助读者掌握用AutoCAD绘制平面图形的方法和技巧。

图5-1 挂轮架平面图形5．1 平面图形的尺寸分析按照尺寸在平面图形中所起的作用，可以将平面图形的尺寸分为定形尺寸和定位尺寸两类。

而要想确定平面图形中各组成线段的上下、左右的相对位置，则必须引入机械制图中被称为尺寸基准的概念。

1. 定形尺寸确定平面图形中各几何元素形状大小的尺寸称为定形尺寸。

如图5-2(a)所示。

2. 定位尺寸用于确定圆心、线段等几何元素在平面图形中所处位置的尺寸称为定位尺寸。

如图5-2(b)所示。

3. 尺寸基准确定平面图形中尺寸位置的点、线等几何元素称为尺寸基准，尺寸基准简称为基准。

一般以平面图形中的对称中心线、圆心、轮廓直线等作为尺寸基准，定位尺寸应以尺寸基准作为标注尺寸的起点。

一个平面图形应有水平和垂直两个方向的尺寸基准，对于较复杂的平面图形，在同一方向上往往有几个基准，其中一个为主要基准，其余为辅助基准。

如图5-1中Φ112的圆心和垂直中心线就是108和30°等尺寸的基准。

(a) 定形尺寸 (b) 定位尺寸图5-2 挂轮架平面图形的尺寸分析5．2 平面图形的线段分析平面图形中的线段通常指直线、圆弧和圆。

平面图形线段分析的实质是通过分析线段的尺寸情况来区分不同类型的线段，并由此确定各线段的作图顺序。

画法几何课件1. 简介画法几何是数学中的一个分支，主要研究平面上点、线、面的相互位置关系以及其相关性质。

它是很多数学领域的基础，如几何学、拓扑学、代数学等。

本课件将介绍画法几何的基础知识、相关概念和常用的绘画方法。

2. 基础概念2.1 点在画法几何中，点是最基本的元素，通常用大写的拉丁字母表示，如A、B、C 等。

点没有大小和形状，只有位置。

2.2 线段线段是由两个点A和B确定的一条有限长度的直线，通常用直线上两点之间加一横线表示，如AB。

2.3 直线直线是由无限多个点确定的一条无限延伸的线段，通常用一条箭头表示，如AB。

2.4 射线射线是由一个点A和一条直线上的任意一点B确定的一条从A点出发，通过B点并且延伸无限远的线段，通常用一条箭头加一横线表示，如→AB。

2.5 平面平面是由无限多个点确定的一个无限延伸的平面，可以想象成一个没有厚度的纸张。

通常用大写的希腊字母表示，如α、β等。

3. 绘图方法3.1 直尺直尺是绘图中最基本的工具之一，用来连接点、绘制线段和射线等。

在画法几何中，我们常用直尺和铅笔进行绘图。

3.2 足量器足量器是一种测量长度的工具，可以用来绘制准确的线段和尺寸。

在画法几何中，常用足量器来测量线段的长短。

3.3 毛笔和颜料毛笔和颜料是绘制曲线和填充颜色的工具，在画法几何中，我们可以使用毛笔和颜料来绘制弧线、曲线和填充形状。

4. 常用形状的绘制4.1 线段的绘制通过直尺和铅笔可以很容易地绘制一条线段，只需要确定起点和终点，然后用直尺连接这两个点即可。

4.2 弧线的绘制弧线是由一条曲线和两个端点确定的，可以通过规定曲率和端点位置来绘制不同形状的弧线。

4.3 多边形的绘制多边形是由若干条线段组成的闭合图形，可以通过逐个连接线段的方式来绘制不同形状的多边形。

4.4 填充颜色可以使用毛笔和颜料来为绘制的图形填充颜色，使图形更加生动和立体。

5. 画法几何的应用5.1 几何问题的求解画法几何在解决几何问题时起到了重要的作用，通过绘制几何图形，可以更加直观地理解和解决相关问题。

第二节平面图形的基本作图方法(建议4课时)考纲要求掌握平面图形的基本作图方法。

知识网络知识要点一、基本几何作图方法(一)等分线段的方法1．平行线法：过所要等分线段的某一端点作一辅助线，两线成任意锐角，在辅助线上截取几等份，连接辅助线端点及所等分线段的端点，在辅助线的各等分点上依次作端点连线的平行线，即将线段分成若干等份。

2．分规试分法：用分规以某一长度试分线段，不断调整分规两脚距离，直至等分完成。

(二)圆的等分1．尺规作图法：运用直尺、圆规，运用几何规律来等分。

要求能对圆周进行三、四、五、六等分的作图。

2．查表计算法：按公式a＝k·D(D为圆直径，k为等分系数)计算出正多边形每边长度，然后依次在圆周上截取，即得。

这种方法适合于任意等分圆周。

(三)椭圆的画法1．同心圆法(理论画法)：先求出曲线上一定数量的点，再用光滑的曲线将各点连接起来。

2．四心法(近似画法)：求出画椭圆的四个圆心和半径，用四段圆弧近似地代替椭圆。

(四)斜度与锥度画法1．斜度：一直线(或平面)对另一直线(或平面)的倾斜程度。

表示符号：∠或>，符号的方向应与斜度的方向一致。

2．锥度：指正圆锥体底圆直径与锥高之比。

表示符号⊲或⊳，符号所示方向应与圆锥方向一致。

3．斜度与锥度的比值均要写成1∶n的形式，如∠1∶n或⊲1∶n。

4．标注锥度时，锥度符号配置在基准线上，表示圆锥的图形符号和锥度应靠近轮廓标注，基准线应通过指引线与圆锥的轮廓素线相连。

基准线应与圆锥的轴线平行，图形符号的方向与圆锥方向一致。

当所标注的锥度是标准圆锥系列之一时，可用标准系列号和相应的标记表示。

(五)圆弧连接1．圆弧连接的实质，就是要使连接圆弧与相邻线段相切，以达到圆弧连接处光滑过渡的要求，切点即为连接点。

2．圆弧连接的基本作图步骤：(1)求作连接圆弧圆心；(2)找切点；(3)画连接圆弧。

作图时第(2)步找切点不要忽视，因为切点是连接圆弧的起点和终点，必须要找出。

5条直线6个交点,三种画法一、五条直线六个交点的三种画法在平面几何中，直线是最基本的几何元素之一，当五条直线相互交叉时，会形成六个交点。

这六个交点可以被连接，形成不同的图形。

本文将介绍三种不同的画法，展示这六个交点的具体位置和关系。

一、画法一：正五边形第一种画法是通过连接这六个交点，构成一个正五边形。

正五边形是一个五边形的特殊形式，其五个顶点均位于一个圆上，并且每个内角都为108度。

在这种画法中，五条直线互相交叉形成六个交点，然后我们按照交点的顺序依次连接它们，最终得到一个准确的正五边形。

二、画法二：星形第二种画法是通过连接这六个交点，构成一个星形。

星形是一种具有对称性的图形，其特点是由多个尖角和锐角组成。

在这种画法中，我们将六个交点按照某种顺序依次连接，形成多个尖角和锐角，最终得到一个六角星形。

三、画法三：六边形第三种画法是通过连接这六个交点，构成一个六边形。

六边形是一个具有六个边和六个顶点的多边形，它具有对称性和稳定性。

在这种画法中，我们将六个交点按照某种顺序依次连接，最终得到一个六边形。

以上是三种基本的画法，通过连接五条直线的六个交点，我们可以得到不同形状的图形。

这些图形在几何学和数学中都有着重要的应用，例如在建筑设计、计算机图形学等领域。

这些图形不仅美观，而且具有一定的几何性质，可以帮助我们更好地理解和应用几何学的知识。

总结：通过连接五条直线的六个交点，我们可以得到不同形状的图形，本文介绍了三种常见的画法：正五边形、星形和六边形。

这些图形具有美观性和几何性质，对于几何学的学习和应用都有着重要的意义。

希望读者通过本文的介绍，能够更好地理解和应用这些几何图形。

第⼆节平⾯图形的基本作图⽅法第⼆节平⾯图形的基本作图⽅法(建议4课时)考纲要求掌握平⾯图形的基本作图⽅法。

知识⽹络知识要点⼀、基本⼏何作图⽅法(⼀)等分线段的⽅法1．平⾏线法：过所要等分线段的某⼀端点作⼀辅助线，两线成任意锐⾓，在辅助线上截取⼏等份，连接辅助线端点及所等分线段的端点，在辅助线的各等分点上依次作端点连线的平⾏线，即将线段分成若⼲等份。

2．分规试分法：⽤分规以某⼀长度试分线段，不断调整分规两脚距离，直⾄等分完成。

(⼆)圆的等分1．尺规作图法：运⽤直尺、圆规，运⽤⼏何规律来等分。

要求能对圆周进⾏三、四、五、六等分的作图。

2．查表计算法：按公式a＝k·D(D为圆直径，k为等分系数)计算出正多边形每边长度，然后依次在圆周上截取，即得。

这种⽅法适合于任意等分圆周。

(三)椭圆的画法1．同⼼圆法(理论画法)：先求出曲线上⼀定数量的点，再⽤光滑的曲线将各点连接起来。

2．四⼼法(近似画法)：求出画椭圆的四个圆⼼和半径，⽤四段圆弧近似地代替椭圆。

(四)斜度与锥度画法1．斜度：⼀直线(或平⾯)对另⼀直线(或平⾯)的倾斜程度。

表⽰符号：∠或>，符号的⽅向应与斜度的⽅向⼀致。

2．锥度：指正圆锥体底圆直径与锥⾼之⽐。

表⽰符号?或?，符号所⽰⽅向应与圆锥⽅向⼀致。

3．斜度与锥度的⽐值均要写成1∶n的形式，如∠1∶n或?1∶n。

4．标注锥度时，锥度符号配置在基准线上，表⽰圆锥的图形符号和锥度应靠近轮廓标注，基准线应通过指引线与圆锥的轮廓素线相连。

基准线应与圆锥的轴线平⾏，图形符号的⽅向与圆锥⽅向⼀致。

当所标注的锥度是标准圆锥系列之⼀时，可⽤标准系列号和相应的标记表⽰。

(五)圆弧连接1．圆弧连接的实质，就是要使连接圆弧与相邻线段相切，以达到圆弧连接处光滑过渡的要求，切点即为连接点。

2．圆弧连接的基本作图步骤：(1)求作连接圆弧圆⼼；(2)找切点；(3)画连接圆弧。

作图时第(2)步找切点不要忽视，因为切点是连接圆弧的起点和终点，必须要找出。

正九边形最简单画法摘要：1.引言2.正九边形的特点3.正九边形的画法4.结论正文：1.引言正九边形是一种有九个边和九个角的平面几何图形。

在数学和艺术领域，正九边形有着广泛的应用。

要绘制一个正九边形，需要掌握一定的技巧和方法。

本文将为大家介绍一种最简单的画正九边形的方法。

2.正九边形的特点正九边形的特点是所有边长相等，所有角度均为140 度。

正九边形的中心角为360/9=40 度。

与正三角形、正方形和正五边形相比，正九边形的角度更为特殊，不易直接计算。

3.正九边形的画法（1）准备工具：直尺、圆规和铅笔。

（2）画一个正方形。

首先，画一条水平线作为基准线。

在这条基准线上选择一个点，作为正方形的一个顶点。

然后，向上画一条与基准线垂直的线段，使其与基准线形成一个直角。

接着，以这个直角为顶点，画一个正方形。

（3）将正方形分割成九个小正方形。

在正方形的每条边上，分别从顶点向内画一条线段，使其与相邻的边形成一个等腰直角三角形。

这样，正方形就被分割成了九个小正方形。

（4）连接小正方形的对角线。

从每个小正方形的顶点开始，向相邻的小正方形的对角线方向画一条线段。

这样，九个小正方形之间就形成了九条相交的线段。

（5）擦去多余的线段。

将分割正方形时画的线段和小正方形之间的线段擦去，留下连接小正方形对角线的线段。

这些线段就构成了一个正九边形。

4.结论通过以上步骤，我们可以用最简单的方法画出一个正九边形。

这种方法易于理解和操作，适用于初学者和需要快速绘制正九边形的场合。

在实际应用中，正九边形还有很多其他画法，例如利用三角函数、作图软件等。

几何图形画法几何图形是由线段、直线、角度等基本几何元素组成的图形。

通过对这些基本元素的组合使用，可以创造出各种形状的几何图形，如矩形、三角形、圆形等。

在绘制几何图形时，需要掌握一些基本的画法，具体如下：1. 直线的画法直线是几何图形中最基本的元素之一。

在画直线时，需要确定直线的起点和终点，在这两点之间，通过尺子或者其他工具画出一条直线。

如果要使直线更加精细，可以用剪刀剪一张纸片，将其对准直线，然后用铅笔沿着纸片边缘画出一条直线。

2. 角度的画法角度是由两条射线组成的几何图形。

在画角度时，需要确定两条射线的起点和终点，然后用尺子或者其他工具连接这些点，形成两条射线。

接着，需要用圆规和直尺画出一个圆弧，使其与两条射线相切，这样就可以得到所需的角度。

3. 三角形的画法三角形是由三条边和三个角组成的几何图形。

在画三角形时，首先需要确定三个顶点的位置，然后通过连接这些点画出三条边。

在这个过程中，需要确保三条边之间的角度符合要求，以保证所画出的是一个合法的三角形。

4. 矩形的画法矩形是由四条边和四个角组成的几何图形。

在画矩形时，需要确定矩形的长和宽，然后画出两条长边和两条短边。

在画长边和短边的过程中，需要确保它们之间的角度是直角。

5. 圆形的画法圆形是由一个圆心和一组等距离的点组成的几何图形。

在画圆形时，需要确定圆心的位置和圆的半径，然后用圆规画出一个圆弧，使其与圆心相切。

通过不断重复这个过程，可以得到一个完整的圆形。

绘制几何图形时，还需要注意以下几点：1. 确定尺寸：在绘制几何图形时，需要明确每个元素的长度、角度等尺寸参数，以确保所画出的图形符合要求。

2. 使用合适的工具：在画直线、角度、圆弧等元素时，需要选择合适的工具，以确保画出的图形精细、清晰。

3. 练习基本技能：几何图形的绘制需要掌握一些基本的技能，如使用尺子、圆规等工具，画直线、角度等元素，需要不断加强练习。

总之，准确、精细绘制几何图形需要掌握基本的绘图技能和细心认真的态度。