中考数学复习圆中的有关计算1[人教版](新编教材)

第２6讲 圆的有关计算一、弧长、扇形面积的计算１、假如弧长为ｌ,圆心角的度数为ｎ°,圆的半径为r ,那么弧长的计算公式为ｌ=_＿____＿___、2、由组成圆心角的两条半径与圆心角所对弧围成的图形叫做扇形、若扇形的圆心角为n °,所在圆半径为r ,弧长为l ,面积为S ,则S ＝_____＿＿＿_＿或Ｓ=１2l ｒ;扇形的周长＝2r +l 、 二、圆柱与圆锥1、圆柱的侧面展开图是＿_____＿___,这个矩形的长等于圆柱的底面圆的_＿__＿_＿＿__,宽等于圆柱的＿＿＿___＿__＿。

假如圆柱的底面半径是ｒ,则S 侧=２πrh ,Ｓ全=２πr ２+2πrh 、２、圆锥的轴截面为由母线、底面直径组成的等腰三角形、圆锥的侧面展开图是一个＿_＿____＿＿_,扇形的弧长等于圆锥的底面圆的_＿__＿＿_＿_＿,扇形的半径等于圆锥的_＿________。

因此圆锥的侧面积:S 侧＝12l ·2πr ＝πｒl (ｌ为母线长,r 为底面圆半径);圆锥的全面积:S 全=S 侧＋S 底＝πrl ＋πr 2。

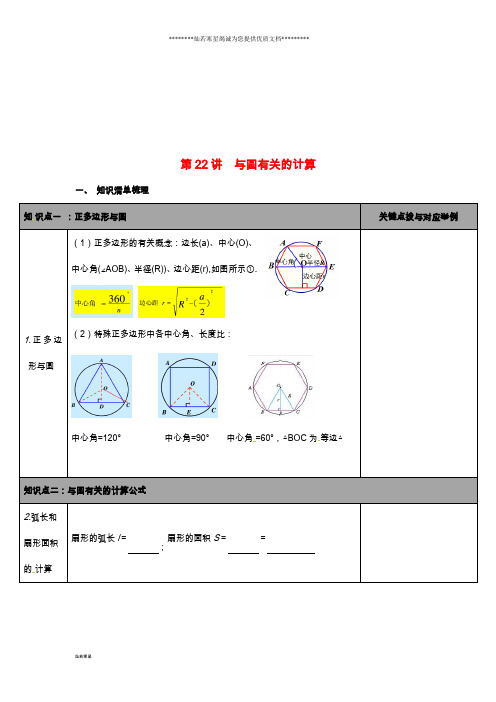
三、正多边形与圆１、正多边形:各边____＿____＿、各角＿___＿__＿＿＿的多边形叫做正多边形。

2、多边形的外接圆:经过多边形__________的圆叫做多边形的外接圆,这个多边形叫做圆的内接多边形、３。

正多边形的__＿____＿__的圆心叫做正多边形的中心,_＿＿___＿_＿_的半径叫做正多边形的半径、4、中心到正多边形的一边的_＿＿___＿＿＿_叫做正多边形的边心距、5、正多边形每一边所对的________＿_的圆心角叫做正多边形的中心角,正n 边形的每个中心角都等于___＿___＿__。

温馨提示(1)正多边形的各边、各角都相等。

(2)正多边形都是轴对称图形,一个正n 边形共有n 条对称轴,每条对称轴都通过正n 边形的中心、(3)边数为偶数的正多边形是中心对称图形,它的中心是对称中心、(４)边数相同的正多边形相似、它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方、四、不规则图形面积的计算求与圆有关的不规则图形的面积时,最基本的思想就是转化思想,即把所求的不规则的图形的面积转化为规则图形的面积、常用的方法有:１、直截了当用公式求解、2、将所求面积分割后,利用规则图形的面积相互加减求解、3。

新人教版初中数学——与圆有关的计算知识点归纳及中考典型题解析一、正多边形的有关概念正多边形中心：正多边形的外接圆的圆心叫做这个正多边形的中心．正多边形半径：正多边形外接圆的半径叫做正多边形半径．正多边形中心角：正多边形每一边所对的圆心角叫做正多边形中心角．正多边形边心距：正多边形中心到正多边形的一边的距离叫做正多边形的边心距．二、与圆有关的计算公式1．弧长和扇形面积的计算扇形的弧长l=π180n r；扇形的面积S=2π360n r=12lr．2．圆锥与侧面展开图（1）圆锥侧面展开图是一个扇形，扇形的半径等于圆锥的母线，扇形的弧长等于圆锥的底面周长．（2）若圆锥的底面半径为r，母线长为l，则这个扇形的半径为l，扇形的弧长为2πr，圆锥的侧面积为S圆锥侧=12ππ2l r rl⋅=．圆锥的表面积：S圆锥表=S圆锥侧+S圆锥底=πrl+πr2=πr·（l+r）．在求不规则图形的面积时，注意利用割补法与等积变化方法归为规则图形，再利用规则图形的公式求解．考向一正多边形与圆任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆．典例1如图，已知⊙O的周长等于8π cm，则圆内接正六边形ABCDEF的边心距OM的长为A．2 cm B．cmC．4 cm D．cm【答案】B【解析】如图，连接OC，OD，∵正六边形ABCDEF是圆的内接多边形，∴∠COD=60°，∵OC=OD，OM⊥CD，∴∠COM=30°，∵⊙O的周长等于8π cm，∴OC=4 cm，∴OM=4cos30°（cm），故选B．【点睛】本题考查了正多边形和圆、正六边形的性质、等腰三角形的判定与性质；熟练掌握正六边形的性质是解决问题的关键．1．若一个正多边形的一个外角为60°，则它的内切圆半径与外接圆半径之比是__________．2．如图，正方形ABCD的外接圆为⊙O，点P在劣弧CD上（不与C点重合）．（1）求∠BPC的度数；（2）若⊙O的半径为8，求正方形ABCD的边长．考向二 弧长和扇形面积1．弧长公式：π180n Rl =； 2．扇形面积公式：2π360n R S =扇形或12S lR =扇形．典例2 如图，A 、B 、C 是圆O 上三个不同的点，且//AO BC ，20OAC ∠=，若1OA =，则AB 长是A ．118π B ．19πC ．29πD ．718π【答案】C【解析】∵AO ∥BC ，∴∠ACB=∠OAC=20°，由圆周角定理，得：∠AOB=2∠ACB=2×20°=40°．∴AB 的长为401180π⨯⨯=29π，故选C ．【名师点睛】本题主要考查了弧长的求解，解题的关键是熟知圆周角定理和平行线的性质． 典例3 如图，一段公路的转弯处是一段圆弧AB ，则AB 的展直长度为A ．3πB ．6πC ．9πD ．12π【答案】B【解析】AB 的展直长度为：10810180π⨯=6π（m ）．故选B ．【名师点睛】此题主要考查了弧长计算，正确掌握弧长公式是解题关键．3．圆心角为240°的扇形的半径为3cm ，则这个扇形的面积是 A ．πcm 2 B ．3πcm 2C ．9πcm 2D ．6πcm 24．如图，从一块直径为2m 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为A ．22m π B ．232m πC ．2m πD ．22m π1．时钟的分针长5cm ，经过15分钟，它的针尖转过的弧长是A ．254πcm B ．152πcm C ．52πcm D ．512πcm 2．如图，正方形ABCD 内接于⊙O ，AB 2，则AB 的长是A ．πB ．32π C ．2π D ．12π 3．圆锥的主视图与左视图都是边长为4的等边三角形，则圆锥的侧面展开图扇形的圆心角是 A ．90°B ．120°C ．150°D ．180°4．已知半径为5的⊙O 是△ABC 的外接圆．若∠ABC =25°，则劣弧AC 的长为A ．25π36 B ．125π36C ．25π18D ．5π365．如图，正六边形ABCDEF 内接于O ，正六边形的周长是12，则O 的半径是A ．3B ．2C ．D ．6．如图，在ABC △中，90ACB ∠=︒，30A ∠=︒，4AB =，以点B 为圆心，BC 长为半径画弧，交AB 于点D ，则CD 的长为A ．1π6B ．1π3C ．2π3D ．π37．如图，AB 是圆锥的母线，BC 为底面半径，已知BC =6 cm ，圆锥的侧面积为15π cm 2，则sin ∠ABC 的值为A ．34B ．35C ．45D ．538．如图，AB 为O 的直径，C 和D 分别是半圆AB 上的三等分点，连接AC AD BC BD 、、、，若2AB =，则图中阴影部分的面积为A ．23π-B ．23π-C ．3π-D ．3π-9．若一个圆锥的底面积为24cm π，圆锥的高为，则该圆锥的侧面展开图中圆心角的度数为 A ．40︒B ．80︒C ．120︒D ．150︒10．如图，在⊙O 的内接四边形ABCD 中，AB AD =，120C ∠=︒，点E 在弧AD 上．若AE 恰好为⊙O 的内接正十边形的一边，DE 的度数为__________．11．小明用如图所示的扇形纸片折叠成一个圆锥的侧面，已知圆锥的母线长为5cm ，扇形的弧长是6πcm ，那么这个圆锥的高是__________．12．如图，I是△ABC的内心，∠B=60°，则∠A I C=__________．13．如图，小明自制一块乒乓球拍，正面是半径为8cm的⊙O，AB=90°，弓形ACB（阴影部分）粘贴胶皮，则胶皮面积为__________．14．如图，正六边形ABCDEF的边长为1，以点A为圆心，AB的长为半径，作扇形ABF，则图中阴影部分的面积为__________（结果保留根号和π）．15．如图1，作∠BPC平分线的反向延长线PA，现要分别以∠APB，∠APC，∠BPC为内角作正多边形，且边长均为1，将作出的三个正多边形填充不同花纹后成为一个图案．例如，若以∠BPC为内角，可作出一个边长为1的正方形，此时∠BPC=90°，而902=45是360°（多边形外角和）的18，这样就恰好可作出两个边长均为1的正八边形，填充花纹后得到一个符合要求的图案，如图2所示．图2中的图案外轮廓周长是__________；在所有符合要求的图案中选一个外轮廓周长最大的定为会标，则会标的外轮廓周长是__________．16．如图，AB 是⊙O 的弦，BC 切⊙O 于点B ，AD ⊥BC ，垂足为D ，OA 是⊙O 的半径，且OA =3．（1）求证：AB 平分∠OAD ；（2）若点E 是优弧AEB 上一点，且∠AEB =60°，求扇形OAB 的面积（计算结果保留π）．17．如图，AB 为⊙O 的直径，C 为⊙O 上一点，∠ABC 的平分线交⊙O 于点D ，DE ⊥BC 于点E ．（1）试判断DE 与⊙O 的位置关系，并说明理由；（2）过点D 作DF ⊥AB 于点F ，若BE DF =3，求图中阴影部分的面积．18．如图，在ABC ∆中，AB AC =，AO BC ⊥于点O ，OE AB ⊥于点E ，以点O 为圆心，OE为半径作半圆，交AO 于点F ． （1）求证：AC 是O 的切线；（2）若点F 是AO 的中点，3OE =，求图中阴影部分的面积；（3）在（2）的条件下，点P 是BC 边上的动点，当PE PF +取最小值时，直接写出BP 的长．19．如图，AB 是O 的直径，AC 是O 的切线，切点为A ，BC 交O 于点D ，点E 是AC 的中点.（1）试判断直线DE 与O 的位置关系，并说明理由；（2）若O 的半径为2，50B ∠=，5AC =，求图中阴影部分的周长.20．如图，C 、D 是半圆O 上的三等分点，直径AB =4，连接AD 、AC ，DE ⊥AB ，垂足为E ，DE 交AC于点F．（1）求∠AFE的度数；（2）求阴影部分的面积（结果保留π和根号）．21．如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC 分别交AM，BN于点D，C，且CB=CE．（1）求证：DA=DE；（2）若AB=6，CD，求图中阴影部分的面积．1．一个扇形的半径为6，圆心角为120°，则该扇形的面积是 A ．2π B ．4πC ．12πD ．24π2．如图，正五边形ABCDE 内接于⊙O ，P 为DE 上的一点（点P 不与点D 重合），则∠CPD 的度数为A ．30°B ．36°C ．60°D ．72°3．如图物体由两个圆锥组成．其主视图中，∠A =90°，∠ABC =105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为A ．2BC ．32D4．如图，在Rt △ABC 中，∠ABC =90°，AB BC =2，以AB 的中点O 为圆心，OA 的长为半径作半圆交AC 于点D ，则图中阴影部分的面积为A 2πB 2πC ．-πD ．-π25．如图是一个圆锥形冰淇淋外壳（不计厚度），已知其母线长为12 cm ，底面圆半径为3 cm ，则这个冰淇淋外壳的侧面积等于__________cm 2（结果精确到个位）．6．如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是__________．（结果保留π）7．如图，在扇形OAB中，半径OA与OB的夹角为120︒，点A与点B的距离为若扇形OAB 恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为__________．8．如图，O为Rt△ABC直角边AC上一点，以OC为半径的⊙O与斜边AB相切于点D，交OA于点E，已知BC，AC=3．则图中阴影部分的面积是__________．9．已知圆锥的底面半径是1__________度．AB=，将半圆绕点A顺时针旋转60︒，点B旋转到点C的位10．如图，AB为半圆的直径，且6置，则图中阴影部分的面积为__________．11．如图，在扇形AOB中，∠AOB=120°，半径OC交弦AB于点D，且OC⊥O A．若OA=则阴影部分的面积为__________．12．《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著，与古希腊的《几何原本》并称现代数学的两大源泉．在《九章算术》中记载有一问题“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”小辉同学根据原文题意，画出圆材截面图如图所示，已知：锯口深为1寸，锯道AB=1尺（1尺=10寸），则该圆材的直径为__________寸．13．如图，在△ABC中，BA=BC，∠ABC=90°，以AB为直径的半圆O交AC于点D，点E是BD上不与点B，D重合的任意一点，连接AE交BD于点F，连接BE并延长交AC于点G．（1）求证：△ADF≌△BDG；（2）填空：①若AB=4，且点E是BD的中点，则DF的长为__________；②取AE的中点H，当∠EAB的度数为__________时，四边形OBEH为菱形．14．如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF ⊥AC，垂足为点F．（1）求证：直线DF是⊙O的切线；（2）求证：BC2=4CF·AC；（3）若⊙O的半径为4，∠CDF=15°，求阴影部分的面积．15．如图，BE是⊙O的直径，点A和点D是⊙O上的两点，连接AE，AD，DE，过点A作射∠=∠．线交BE的延长线于点C，使EAC EDA（1）求证：AC是⊙O的切线；==（2）若CE AE1．【答案】C【解析】∵分针经过60分钟，转过360°，∴经过15分钟转过360°×1560=90°， 则分针的针尖转过的弧长是l C ． 2．【解析】（1）连接OB ，OC ，∵四边形ABCD 为正方形，∴∠BOC =90°， ∴∠P =12∠BOC =45°； （2）过点O 作OE ⊥BC 于点E ，∵OB =OC ，∠BOC =90°，∴∠OBE =45°，∴OE =BE ，∵OE 2+BE 2=OB 2，∴BE ==∴BC=2BE=2×=．【点睛】垂径定理：垂直于弦的直径平分弦并且平分弦所对的两条弧．3．【答案】D【解析】扇形面积的计算公式为：2π2409S6π360360n rπ⨯⨯===，故选D．4．【答案】A【解析】连接AC．∵从一块直径为2m的圆形铁皮上剪出一个同心角为90°的扇形，即∠ABC=90°，∴AC为直径，即AC=2m，AB=BC．∵AB2+BC2=22，∴AB=BCm，∴阴影部分的面积是290360π⨯=12π（m2）．故选A．【名师点睛】本题考查了圆周角定理和扇形的面积计算，能熟记扇形的面积公式是解答此题的关键．1．【答案】C【解析】∵25B∠=︒，∴50O∠=︒，∵//AB CO，∴50O A∠=∠=︒，故选C.【名师点睛】本题主要考查了圆周角定理及平行线的性质，熟练运用相关知识点是解决本题的关键.2．【答案】A【解析】如图，连接OA、OB，∵正方形ABCD内接于⊙O，∴AB=BC=DC=AD，∴AB BC CD DA===，∴∠AOB=14×360°=90°，在Rt△AOB中，由勾股定理得：2AO2=（）2，解得：AO=2，∴AB的长为90π2180⨯=π，故选A．3．【答案】D【解析】∵圆锥的主视图与左视图都是边长为4的等边三角形，∴圆锥的母线长为4，底面圆的直径为4，则圆锥的侧面展开图扇形的半径为4，设圆锥的侧面展开图扇形的圆心角是n，根据题意，得：·π·4180n=4π，解得：n=180°，故选D．4．【答案】C【解析】如图，连接AO，CO，∵∠ABC=25°，∴∠AOC=50°，∴劣弧AC的长=50π525π=18018⨯，故选C．5．【答案】B【解析】如图，连结OA，OB，∵ABCDEF 为正六边形，∴∠AOB =360°×16=60°，∴△AOB 是等边三角形， ∵正六边形的周长是12，∴AB =12×16=2，∴AO =BO =AB =2，故选B ．【名师点睛】本题考查了正多边形和圆，以及正六边形的性质，根据题意画出图形，作出辅助线求出∠AOB =60°是解答此题的关键. 6．【答案】C【解析】∵90ACB ∠=︒，4AB =，30A ∠=︒，∴60B ∠=︒，2BC =， ∴CD 的长为60π22π1803⨯=，故选C ． 7．【答案】C【解析】设圆锥的母线长为R ，由题意得15π=π×3×R ，解得R =5， ∴圆锥的高为4，∴sin ∠ABC =45．故选C ． 8．【答案】B【解析】设AD BC 、相交于点,E C 和D 分别是半圆AB 上的三等分点，AB 为⊙O 的直径30ABC BAD ∴∠=∠=︒.90ACB BDA ∠=∠=︒.2AB =，1,AC BD ∴==32ABC ABDBC AD SS==∴==，如图，连接OE ，则OE AB ⊥，1,AO BO OE ==∴=122ABES∴==，2222ABC ABES S S Sππ∴=-+=-+=-阴影半圆， 故选B .【名师点睛】此题主要考查了半圆的面积、圆的相关性质及在直角三角形中，30°角所对应的边等于斜边的一半，关键记得加上△ABE 的面积是解题的关键.9．【答案】C【解析】∵圆锥的底面积为4πcm 2，∴圆锥的底面半径为2cm ，∴底面周长为4π，圆锥的高为cm ， ∴由勾股定理得圆锥的母线长为6cm ， 设侧面展开图的圆心角是n °， 根据题意得：6180n π=4π，解得：n =120．故选C ． 【名师点睛】本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长． 10．【答案】84︒【解析】如图，连接BD ，OA ，OE ，OD ，∵四边形ABCD 是圆的内接四边形，∴180BAD C ∠+∠=︒， ∵120C ∠=︒，∴60BAD ∠=︒，∵AB AD =，∴ABD △是正三角形，∴60ABD ∠=︒，2120AOD ABD ∠=∠=︒， ∵AE 恰好是⊙的内接正十边形的一边，∴3603610AOE ︒∠==︒， ∴1203684DOE ∠=︒-︒=︒，∴DE 的度数为84°．故答案为：84°．11．【答案】4cm【解析】设圆锥的底面半径是r ，则2πr =6π，解得：r =3，cm ）． 【点睛】本题主要考查圆锥侧面展开图的计算．用到的知识点：圆锥的侧面展开图是一个扇形，扇形的弧长等于圆锥底面的周长，扇形的半径是圆锥的母线长． 12．【答案】120°．【解析】∵∠B =60°，∴∠BAC +∠BCA =120°∵三角形的内切圆的圆心是三角形三个角的平分线的交点，∴∠I AC =12∠BAC ，∠I CA =12∠BCA ， ∴∠I AC +∠I CA =12（∠BAC +∠BCA ）=60°，∴∠A I C =180°﹣60°=120°，故答案为120°．【名师点睛】此题主要考查利用三角形的内切圆的圆心是三角形三个角的平分线的交点性质进行角度求解，熟练掌握，即可解题. 13．【答案】（32+48π）cm 2【解析】如图，连接OA 、OB ，∵AB =90°，∴∠AOB =90°，∴S △AOB =12×8×8=32（cm 2）， 扇形ACB （阴影部分）=2270π8360⨯⨯=48π（cm 2），则弓形ACB 胶皮面积为（32+48π）cm 2， 故答案为：（32+48π）cm 2．14-π3 【解析】正六边形的中心为点O ，如图，连接OD 、OE ，作OH ⊥DE 于H ，∴∠DOE =3606︒=60°，∴OD =OE =DE =1，∴OH∴正六边形ABCDEF 的面积=12×，∠A =(62)1806-⨯︒=120°，∴扇形ABF 的面积=2120π13π603⨯=，∴图中阴影部分的面积=2-π3，故答案为：2-π3． 15．【答案】14；21【解析】图2中的图案外轮廓周长是：8-2+2+8-2=14； 设∠BPC =2x ，∴以∠BPC 为内角的正多边形的边数为：360180180290x x =--，以∠APB 为内角的正多边形的边数为：360x，∴图案外轮廓周长是=18090x --2+360x -2+360x -2=18090x -+720x-6，根据题意可知：2x 的值只能为60°，90°，120°，144°， 当x 越小时，周长越大，∴当x =30时，周长最大，此时图案定为会标， 则则会标的外轮廓周长是=180720903030+--6=21，故答案为：14；21．16．【解析】（1）连接OB ，如图所示：∵BC 切⊙O 于点B ，∴OB ⊥BC ，∵AD ⊥BC ，∴AD ∥OB ，∴∠DAB =∠OBA ，∵OA =OB ，∴∠OAB =∠OBA ，∴∠DAB =∠OAB ，∴AB 平分∠OAD ； （2）∵点E 是优弧AEB 上一点，且∠AEB =60°， ∴∠AOB =2∠AEB =120°，∴扇形OAB 的面积=2120π3360⨯=3π． 17．【解析】（1）DE 与⊙O 相切，理由：如图，连接DO ，∵DO =BO ， ∴∠ODB =∠OBD ，∵∠ABC 的平分线交⊙O 于点D ， ∴∠EBD =∠DBO ， ∴∠EBD =∠BDO ， ∴DO ∥BE ， ∵DE ⊥BC ，∴∠DEB =∠EDO =90°， ∴DE 与⊙O 相切．（2）∵∠ABC 的平分线交⊙O 于点D ，DE ⊥BE ，DF ⊥AB ， ∴DE =DF =3，∵BE∴BD =6， ∵sin ∠DBF =31=62， ∴∠DBA =30°， ∴∠DOF =60°，∴sin60°=3DF DO DO ==∴DO则FO ，132π2-=． 18．【解析】（1）如图，过O 作AC 垂线OM ，垂足为M ．∵AB AC =，AO BC ⊥， ∴AO 平分BAC ∠，∵OE AB OM AC ⊥⊥，， ∴OE OM =， ∵OE 为⊙O 的半径， ∴OM 为⊙O 的半径， ∴AC 是⊙O 的切线．（2）∵3OM OE OF ===，且F 是OA 的中点，∴6AO =，AE =∴2AEO S AO AE =⋅÷=△， ∵OE AB ⊥，∴60EOF ∠=︒，即9π603π3602OEF S ⋅︒==︒扇形，∴3π2S =阴影． （3）作B 关于BC 的对称点G ，交BC 于H ，连接FG 交BC 于P ，此时PE PF +最小， 由（2）知60EOF ∠=︒，30EAO ∠=︒， ∴60B ∠=︒， ∵3EO =，∴3EG =，32EH =，BH =， ∵EG BC ⊥，FO BC ⊥， ∴EHP △∽FOP △， ∴31322EH HP FO PO ==÷=，即2HP OP =，∵BO HP OP=+=，∴3HP=HP=，∴22BP=+=19．【解析】（1）直线DE与⊙O相切，理由如下：连接OE、OD，如图，∵AC是⊙O的切线，∴AB⊥AC，∴∠OAC=90°，∵点E是AC的中点，O点为AB的中点，∴OE∥BC，∴∠1=∠B，∠2=∠3，∵OB=OD，∴∠B=∠3，∴∠1=∠2，在△AOE和△DOE中，∵OA=OD，∠1=∠2，OE=OE，∴△AOE≌△DOE（SAS），∴∠ODE=∠OAE=90°，∴DE⊥OD，∵OD为⊙O的半径，∴DE为⊙O的切线；（2）∵DE、AE是⊙O的切线，∴DE=AE，∵点E是AC的中点，∴DE=AE=12AC=2.5，∵∠AOD=2∠B=2×50°=100°，∴阴影部分的周长=100210 2.5 2.551809ππ⨯++=+．【名师点睛】本题考查的是切线的判定与性质、全等三角形的判定和性质、三角形的中位线、切线长定理、弧长的计算，掌握切线的性质与判定、弧长公式是解题的关键．20．【解析】（1）如图，连接OD，OC，∵C、D是半圆O上的三等分点，∴AD=CD=BC，∴∠AOD=∠DOC=∠COB=60°，∴∠CAB=30°，∵DE ⊥AB ，∴∠AEF =90°，∴∠AFE =90°–30°=60°； （2）由（1）知，∠AOD =60°，∵OA =OD ，AB =4，∴△AOD 是等边三角形，OA =2，∵DE ⊥AO ，∴DE∴S 阴影=S 扇形AOD –S △AOD =260π2360–12×2321．【解析】（1）如图，连接OE 、BE ，∵OB =OE ， ∴∠OBE =∠OE B ． ∵BC =EC ， ∴∠CBE =∠CEB ， ∴∠OBC =∠OEC ． ∵BC 为⊙O 的切线， ∴∠OEC =∠OBC =90°． ∵OE 为半径， ∴CD 为⊙O 的切线， ∵AD 切⊙O 于点A ， ∴DA =DE ．（2）如图，连接OC ，过点D 作DF ⊥BC 于点F ，则四边形ABFD 是矩形， ∴AD =BF ，DF =AB =6，∴DC=BC+AD∵CF=∴BC-AD，∴BC在直角△OBC中，tan∠BOC=BC OB∴∠BOC=60°．在△OEC与△OBC中，OE OB OC OC CE CB=⎧⎪=⎨⎪=⎩，∴△OEC≌△OBC（SSS），∴∠BOE=2∠BOC=120°，∴S阴影部分=S四边形BCEO-S扇形OBE=2×12BC·OB-2120π360OB⋅⋅3π．1．【答案】C【解析】S=2120π6360⨯⨯=12π，故选C．2．【答案】B【解析】如图，连接OC，OD．∵ABCDE是正五边形，∴∠COD=3605︒=72°，∴∠CPD=12∠COD=36°，故选B．3．【答案】D【解析】∵∠A=90°，AB=AD，∴△ABD为等腰直角三角形，∴∠ABD=45°，BD AB，∵∠ABC=105°，∴∠CBD=60°，而CB=CD，∴△CBD为等边三角形，∴BC=BDAB，∵上面圆锥与下面圆锥的底面相同，∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB∶CB，∴下面圆锥的侧面积×．故选D．4．【答案】A【解析】∵在Rt△ABC中，∠ABC=90°，AB，BC=2，∴tan A=BCAB==，∴∠A=30°，∴∠DOB=60°，∵OD=12ABDE=32，3222π-=-，故选A．5．【答案】113【解析】这个冰淇淋外壳的侧面积=12×2π×3×12=36π≈113（cm2）．故答案为：113．6．【答案】π-1【解析】如图，延长DC，CB交⊙O于M，N，则图中阴影部分的面积=14×（S圆O-S正方形ABCD）=14×（4π-4）=π-1，故答案为：π-1．7．【答案】43【解析】如图，连接AB，过O作OM AB⊥于M，∵120AOB∠=︒，OA OB=，∴30BAO ∠=︒，AM =2OA =， ∵240π22π180r ⨯=，∴43r =，故答案为：43．【名师点睛】本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键． 8．【答案】6π【解析】在Rt ABC △中，∵BC =，3AC =．∴AB =，∵BC OC ⊥，∴BC 是圆的切线，∵O 与斜边AB 相切于点D ，∴BD BC =，∴AD AB BD =-==在Rt ABC △中，∵1sin2BC A AB ===，∴30A ∠=︒， ∵O 与斜边AB 相切于点D ，∴⊥OD AB ，∴9060AOD A ∠=︒-∠=︒，∵tan tan 30OD AAD ==︒=，∴1OD =， ∴260π13606πS ⨯==阴影．故答案为：6π．【名师点睛】本题考查了切线的性质定理、切线长定理以及勾股定理、解直角三角形的运用，熟记和圆有关的各种性质定理是解题的关键． 9．【答案】90【解析】设圆锥的母线为a ，根据勾股定理得，a =4， 设圆锥的侧面展开图的圆心角度数为n ︒，根据题意得π42π1180n ⨯⨯=，解得90n =， 即圆锥的侧面展开图的圆心角度数为90︒．故答案为：90．【名师点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长． 10．【答案】6π【解析】由图可得，图中阴影部分的面积为：22260π6π(62)π(62)6π36022⨯⨯⨯÷⨯÷+-=，故答案为：6π．【名师点睛】本题考查扇形面积的计算、旋转的性质，解答本题的关键是明确题意，利用数形结合的思想解答．11π【解析】如图，作OE ⊥AB 于点F ，∵在扇形AOB 中，∠AOB =120°，半径OC 交弦AB 于点D ，且OC ⊥O A ．OA = ∴∠AOD =90°，∠BOC =90°，OA =OB ，∴∠OAB =∠OBA =30°，∴OD =OA ·tan30°=3=2，AD =4，AB =2AF =2×2=6，OF ，∴BD =2，∴阴影部分的面积是：S △AOD +S 扇形OBC -S △BDO =2230π2π23602⨯+-=，π． 12．【答案】26【解析】设⊙O 的半径为r ．在Rt △ADO 中，AD =5，OD =r -1，OA =r ，则有r 2=52+（r -1）2，解得r =13，∴⊙O 的直径为26寸，故答案为：26．13．【解析】（1）∵BA =BC ，∠ABC =90°，∴∠BAC =45°， ∵AB 是⊙O 的直径， ∴∠ADB =∠AEB =90°，∴∠DAF +∠BGD =∠DBG +∠BGD =90°， ∴∠DAF =∠DBG ， ∵∠ABD +∠BAC =90°， ∴∠ABD =∠BAC =45°，∴AD =BD ， ∴△ADF ≌△BDG ．（2）①如图2，过F 作FH ⊥AB 于H ，∵点E 是BD 的中点， ∴∠BAE =∠DAE ， ∵FD ⊥AD ，FH ⊥AB ， ∴FH =FD ，∵FH BF =sin ∠ABD =sin45°=2，∴2FD BF =，即BF FD ， ∵AB =4，∴BD =4cos45°，即BF +FD +1）FD ，∴FD=4-故答案为：4-． ②连接OH ，EH ，∵点H 是AE 的中点，∴OH ⊥AE ，∵∠AEB =90°，∴BE ⊥AE ，∴BE ∥OH ，∵四边形OBEH 为菱形，∴BE =OH =OB =12AB ， ∴sin ∠EAB =BE AB =12， ∴∠EAB =30°．故答案为：30°．14．【解析】（1）如图所示，连接OD ，∵AB =AC ，∴∠ABC =∠C ，而OB =OD ，∴∠ODB =∠ABC =∠C ，∵DF ⊥AC ，∴∠CDF +∠C =90°，∴∠CDF +∠ODB =90°，∴∠ODF =90°，∴直线DF 是⊙O 的切线．（2）连接AD ，则AD ⊥BC ，则AB =AC ，则DB =DC =12BC ， ∵∠CDF +∠C =90°，∠C +∠DAC =90°，∴∠CDF =∠DCA ，而∠DFC =∠ADC =90°，∴△CFD ∽△CDA ，∴CD 2=CF ·AC ，即BC 2=4CF ·AC ． （3）连接OE ，∵∠CDF =15°，∠C =75°，∴∠OAE =30°=∠OEA ， ∴∠AOE =120°，S △OAE =12AE ·OE ·sin ∠OEA =12×2×OE ×cos ∠OEA ×OE sin ∠OEA =S 阴影部分=S 扇形OAE -S △OAE =120360︒︒×π×42-16π3- 15．【解析】（1）如图，连接OA ，过O 作OF AE ⊥于F ，∴90AFO ∠=︒，∴90EAO AOF ∠+∠=︒，∵OA OE =， ∴12EOF AOF AOE ∠=∠=∠， ∵12EDA AOE ∠=∠， ∴EDA AOF ∠=∠，∵EAC EDA ∠=∠，∴EAC AOF ∠=∠，∴90EAO EAC ∠+∠=︒，∵EAC EAO CAO ∠+∠=∠，∴90CAO ∠=︒，∴OA AC ⊥，∴AC 是⊙O 的切线．（2）∵CE AE ==C EAC ∠=∠，∵EAC C AEO ∠+∠=∠，∴2AEO EAC ∠=∠，∵OA OE =，AEO EAO ∠=∠，∴2EAO EAC ∠=∠，∵90EAO EAC ∠+∠=︒，∴30EAC ∠=︒，60EAO ∠=︒，∴OAE △是等边三角形，∴OA AE =，60EOA ∠=︒，∴OA =，∴260π2π360=AOE S ⋅⨯=扇形，在Rt OAE △中，sin 32OF OA EAO =⋅∠==，∴11322AOE S AE OF =⋅=⨯=△∴阴影部分的面积=2π-【名师点睛】此题主要考查圆的切线与扇形面积的求解，解题的关键是熟知圆的性质及判定定理．。

中考数学复习第30课时《与圆有关的计算》教案一. 教材分析《与圆有关的计算》是中考数学的重要内容之一，主要包括圆的周长、面积、弧长、扇形的面积等计算方法。

这部分内容在中考中占有较大比重，是学生必须掌握的知识点。

通过本节课的学习，使学生理解圆的计算方法，提高解决实际问题的能力。

二. 学情分析学生在学习本节课之前，已经掌握了相似多边形的性质、圆的定义、圆的性质等基础知识。

但部分学生在理解圆的计算方法，尤其是涉及到圆的周长、面积等公式的灵活运用上还存在困难。

因此，在教学过程中，教师需要关注学生的学习情况，针对性地进行辅导。

三. 教学目标1.理解圆的周长、面积、弧长、扇形的面积等计算方法。

2.能够灵活运用圆的计算公式解决实际问题。

3.提高学生的数学思维能力和解决问题的能力。

四. 教学重难点1.圆的周长、面积公式的理解和运用。

2.弧长、扇形面积的计算方法。

五. 教学方法1.采用问题驱动法，引导学生主动探究圆的计算方法。

2.利用多媒体辅助教学，直观展示圆的计算过程。

3.采用小组合作学习，培养学生团队合作精神。

4.注重个体差异，针对性地进行辅导。

六. 教学准备1.多媒体教学设备。

2.教学课件。

3.练习题。

七. 教学过程1.导入（5分钟）利用多媒体展示生活中的圆形物体，如硬币、地球等，引导学生关注圆的周长和面积。

提问：你知道这些物体的周长和面积是如何计算的吗？2.呈现（10分钟）讲解圆的周长和面积公式，以及如何运用这些公式解决实际问题。

通过例题，展示圆的周长和面积的计算过程。

3.操练（10分钟）学生独立完成练习题，巩固圆的周长和面积的计算方法。

教师巡回指导，针对性地进行辅导。

4.巩固（5分钟）针对学生练习中出现的问题，进行讲解和辅导。

再次强调圆的周长和面积公式的运用。

5.拓展（10分钟）讲解弧长和扇形面积的计算方法，引导学生运用所学知识解决实际问题。

6.小结（5分钟）对本节课的主要内容进行总结，强调圆的计算方法及其应用。