2015年数学模拟试卷(14)

2015年模拟数学试题卷（全卷三个大题，共23小题，共6页；满分120分，考试时间120分钟）参考公式：二次函数y=ax 2+bx+c 的顶点坐标是)4ab 4ac ,2a b (2--．一、选择题（本题有8小题，每小题3分，共24分.请选出各题中唯一的正确选项，不选、多选、错选， 均不给分） 1．﹣3的相反数为（ ）A 、3B 、13C 、﹣3D 、13-2．已知地球上海洋面积约为316 000 000km 2，316 000 000这个数用科学记数法可表示为( ) A ．3.16×109 B ．3.16×108 C ．3.16×107 D ．3.16×106 3．如图所示的是零件三通的立体图，则这个几何体的俯视图是（ ）A B C D4．已知反比例函数1y x-=，下列结论中正确的是（ ）A .图象经过点（1，1）B .图象在第一、三象限C .当1>x 时，10y -<<D .当0<x 时，y 随着x 的增大而减小5．如图，在Rt △ABC 中，90C ∠=︒，4AC =，3BC =，则tan A 的值为（ ） A ．34 B ．43 C ．35 D ．456．已知圆锥的母线长为5，底面半径为3，则圆锥的表面积为（ ） A ．15π B ．24π C ．30π D ．39π7．已知⊙O 1和⊙O 2的半径分别为2cm 和5cm ，两圆的圆心距是3cm ，则两圆的位置关系是（ ）A ．内含B ．外切C ．内切D ．相交8．某班体育委员调查了本班46名同学一周的平均每天体育活动时间，并制作了如图所示的频数分布直方图，从直方图中可以看出，该班同学这一周的平均每天体育活动时间的中位数和众数依次是（ ）A ．40分，40分B ．50分，40分C ．50分，50分D ．40分，50分（第5题图）主视方向（第3题图）6(第16题图）二、填空题（本题有6小题，每小题3分，共18分） 9．计算：23()a ．10．如图，已知//,,35AB CD BC ABE C BEC ∠∠=︒∠平分，则的度数是 ． 11．某校艺术节演出中，5位评委给某个节目打分如下：9分，9.2分，8.9分，8.8分，9.1分，则该节目的平均得分是分．12．阳阳从家到学校的路程为2400米，他早晨8点离开家，要在8点30分到8点40分之间到学校，如果用x 表示他的速度（单位：米/分），则x 的取值范围为 ． 13．如图，在平面直角坐标系xoy 中，直线AB 过点A （－4，0），B （0，4），⊙O 的半径O 为坐标原点），点P 在直线AB 上，过点P 作⊙O 的一条切线PQ ，Q 为切点，则切线长PQ 的 最小值为 ．14．如图，已知直线y ＝2x ＋6交y 轴于点A ，点B 是这条直线上的一点，并且位于第一象限，点P 是直线x=8上的一动点，若△APB 是等腰直角三角形，则点B 的坐标为 ．三、简答题(本题有9小题，共78分)15．（本题10分）（1）计算：101()(2013)3π-+-+ （2）解方程：xx x -=+--23123(第8题图)（第12题图）AD(第15题图)16．（本题6分）如图，图①，图②均为76 的正方形网格，点A ，B ，C 在格点（小正方形的顶点）上．（1）在图①中确定格点D ，并画出一个以A ，B ，C ，D 为顶点的四边形，使其为轴对称图形；（2）在图②中确定格点E ，并画出一个以A ，B ，C ，E 为顶点的四边形，使其为中心对称图形．17．（本题8分）如图，在□ABCD 中，分别延长BA ，DC 到点E ，使得AE=AB ，CH=CD ，连接EH ，分别交AD ，BC 于点F ,G 。

2015高考文科数学模拟试卷及答案解析目录2015高考文科数学模拟试卷 ......................................................................... 1 2015高考文科数学模拟试卷答案解析 (5)2015高考文科数学模拟试卷（本试卷共4页，21小题，满分150分．考试用时120分钟．）参考公式：锥体的体积公式13V Sh =，其中S 为柱体的底面积，h 为锥体的高．一、选择题（本大题共10小题，每小题5分，满分50分.每小题给出的四个选项中，只有一项是符合题目要求.）1．复数1iZ i=+（其中i 为虚数单位）的虚部是 （ ） A.12- B.12i C.12 D.12i -2．已知集合(){}lg 3A x y x ==+，{}2B x x =≥，则A B =（ ） A. (3,2]- B.(3,)-+∞ C.[2,)+∞ D.[3,)-+∞ 3．下列函数在定义域内为奇函数的是（ ） A. 1y x x=+B. sin y x x =C. 1y x =-D. cos y x = 4.命题“21,11x x <<<若则-”的逆否命题是（ ）A.21,1,1x x x ≥≥≤-若则或B.若11<<-x ，则12<xC.若1x >或1x <-，则12>xD.若1x ≥或1x ≤-，则12≥x 5．若向量(1,2),BA =(4,5),CA =则BC =A.(5,7)B.(3,3)--C.(3,3)D.(5,7)--6．若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算，得数据如下：那么方程220x x x +--=的一个最接近的近似根为（ ） A ．1.2 B ．1.3 C ．1.4 D ．1.57．执行如图所示的程序框图,若输入n 的值为7,则输出的s 的值为（ ） A ．22 B ．16 C ．15 D ．11（7题） （8题）8．函数())(,0,)2f x x x Rπωϕωϕ=+∈><的部分图象如图所示，则,ωϕ的值分别是（ ） A ．2,3π-B.2,6π-C.4,6π-D. 4,3π9．若双曲线22221x y a b-= ）A.2±B.12±D.2± 10．已知函数222,0()()()2(1),2,0x x x f x f a f a f x x x ⎧+≥⎪=-+≤⎨-<⎪⎩,若则实数a 的取值范围是 A.[)1,0- B.[]0,1 C.[]1,1- D.[]2,2-二、填空题：（本大题共5小题，考生作答4小题，每小题5分，满分20分.） （一）必做题（11～13题） 11. 计算33log 18log 2-= ．12．变量x 、y 满足线性约束条件222200x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩，则目标函数z x y =+的最大值为 .13（二）选做题：第14、15全答的，只计前一题的得分。

2015年浙江省高考数学(文科)模拟试题满分150分，考试时间120分钟。

参考公式： 球的表面积公式 S=4πR 2球的体积公式 V=43πR 3 其中R 表示球的半径 锥体的体积公式 V=13Sh 其中S 表示锥体的底面积，h 表示锥体的高柱体的体积公式 V=Sh其中S 表示柱体的底面积，h 表示柱体的高 台体的体积公式 V=13h(S 12) 其中S 1，S 2分别表示台体的上、下底面积， h 表示台体的高如果事件A ，B 互斥，那么 P(A+B)=P(A)+P(B)选择题部分 (共50分)一、 选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1、已知全集U R =，{22}M x x =-≤≤，{1}N x x =<，那么M N =（ ）A ．{21}x x -≤<B ．{21}x x -<<C ．{2}x x <-D ．{|2}x x ≤ 2.已知i 是虚数单位，则i i+-221等于( ) A.i -B.i -54C.i 5354-D.i3、等比数列{}n a 中，01>a ，则“41a a <”是“53a a <” 的（ ）A.充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件 4、已知函数()sin f x x π=的图像一部分如下方左图，则下方右图的函数图像所对应的解析式为 （ ）A 、1(2)2y f x =- B 、(21)y f x =- C 、(1)2x y f =- D 、1()22x y f =- ····5．设m 、n 是两条不同的直线,α、β是两个不同的平面，考察下列命题，其中真命题是（ ）A ．,,m m n n αβαββ⊥=⊥⇒⊥ B ． α∥β,,m α⊥n ∥βm n ⇒⊥C ．,,m n αβα⊥⊥∥βm n ⇒⊥D ． ,,m n m n αβαβ⊥⊂⊥⇒⊥6．从1，2，3，4这四个数字中依次取(不放回)两个数a ，b ，使得a 2≥4b 的概率是（）A ．31B ．512 C ．21D ．7127．已知一个空间几何体的三视图如右图，其中主视图，侧视图都是由半圆和矩形组成，根据图中标出的尺寸，可得这个几何体的表面积是（ ） A 、3π B、 C 、6π D 、5π8．若正数x ，y 满足x 2＋3xy －1＝0，则x ＋y 的最小值是（ ）A ．32B ．322C ．33D ．3329．一个半径为2的球放在桌面上，桌面上的一点1A 的正上方有一个光源A ，1AA 与球相切，16AA =，球在桌面上的投影是一个椭圆，则这个椭圆的离心率等于 （ ） A ．12 B C D10．设a ，b 为单位向量，若向量c 满足|c －(a ＋b)|＝|a －b |，则|c |的最大值是（）A ．1BC ．2D ．主观图侧视图B 1A 21B 2非选择题部分 (共100分)二、 填空题：本大题共7小题，每小题4分，共28分．11．甲、乙两名同学在5次数学考试中，成绩统计用茎叶图表示如图所示，若甲、乙两人的 平均成绩分别为_____________．12．函数f(x)＝223xx a m +-+(a>1)恒过点(1,10)，则m ＝________.13．如图所示，程序框图(算法流程图)的输出值x ＝________. 14．若实数x ，y 满足⎩⎪⎨⎪⎧2x －y ≥0，y ≥x ，y ≥－x ＋b ，且z ＝2x ＋y 的最小值为3，则实数b 的值为________.15．已知点O(0，0)，A(2，0)，B(－4，0)，点C 在直线l ：y ＝－x 上．若CO 是∠ACB 的平分线，则点C 的坐标为________． 16．设A(4，0)，B(0，3)，直线l ：y ＝19196ax ，圆C ：(x －a)2＋y 2＝9．若圆C 既与线段AB 又与直线l 有公共点，则实数a 的取值范围是________．17．已知函数f (x)＝12x 4－2x 3＋3m ，x ∈R ，若f (x)＋9≥0恒成立，则实数m 的取值范围是________．三、 解答题: 本大题共5小题，共72分．解答应写出文字说明、证明过程或演算步骤． 18．(本题满分14分)在△ABC 中，已知cos A ＝35.(1)求sin 2A2－cos(B ＋C)的值；(2)若△ABC 的面积为4，AB ＝2，求BC 的长．19．(本题满分14分)已知在正项数列{a n }中，a 1＝2，点A n (a n ，a n ＋1)在双曲线y 2－x2＝1上，数列{b n }中，点(b n ，T n )在直线y ＝－12x ＋1上，其中T n 是数列{b n }的前n 项和．(1)求数列{a n }的通项公式； (2)求证：数列{b n }是等比数列； (3)若c n ＝a n ·b n ，求证：c n ＋1<c n .20．(本题满分15分)如图，在四棱锥P —ABCD 中，PD ⊥平面ABCD ，AD ⊥CD ，DB 平分∠ADC ，E 为PC 的中点，AD ＝CD ＝1，DB ＝2 2.(1)证明PA ∥平面BDE ； (2)证明AC ⊥平面PBD ；(3)求直线BC 与平面PBD 所成的角的正切值.21．(本题满分15分)已知x ＝1是函数f (x)＝mx 3－3(m ＋1)x 2＋nx ＋1的一个极值点，其中m 、n ∈R ，m<0.(1)求m 与n 的关系表达式； (2)求f (x)的单调区间；(3)当x ∈[－1,1]时，函数y ＝f (x)的图象上任意一点的切线斜率恒大于3m ，求m 的取值范围．22．(本题满分14分)已知定点F(0,1)和直线l 1：y ＝－1，过定点F 与直线l 1相切的动圆的圆心为点C.(1)求动点C 的轨迹方程；(2)过点F 的直线l 2交轨迹于两点P,Q,交直线l 1于点R ，求RP →·RQ →的最小值．参考答案一、选择题: 本题考查基本知识和基本运算。

2015年初中毕业生中考仿真模拟测试数学试卷2015.02温馨提示：1. 全卷共三大题，24小题，满分为150分.考试时间为120分钟，本次考试采用闭卷形式； 2．全卷分为卷Ⅰ（选择题）和卷Ⅱ（非选择题）两部分，全部在答题卷上作答，在试题卷上作答一律无效。

3．参考公式：二次函数2y ax bx c =++图像的顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭. 卷 Ⅰ一、选择题（本题有10小题，每小题4分,共40分）1. 计算：23）（a 的结果是（ ） A ．6a 2 B ．9a C ．5a 2 D ．9a 22.据报道，四川雅安地震，经初步统计，导致的经济损失约1 880 000 000元。

经济损失总额用科学计数法表示为（ ）A.18.8×108B.188×107C.1.88×109D.1.9×109 3. ﹣2011的相反数是（ ）A 、﹣2011B 、2011C 、20111-D 、201114. 如下左图所示的几何体的府视图是（ ）5．已知点P （1 , 2）落在函数y=kx-2的图象上，则k 的值为（ ） A ．2k = B ．3=k C ．4k = D ．6=k6．对于二次函数y=1122+--）（x 下列说法正确的是（ ） A 、当x =1时有最大值1 B 、当x =1时有最小值1 C 、当x =-1时有最大值1 D 、当x =-1时有最小值-17. 已知圆锥的底面半径是3cm ，母线长为4cm ，则侧面积为（ ） A ．6π B ．7π C ．8π D ．12π8. 如图，AD 是⊙O 的直径，点B 、C 是弧ABD 的三等分点，则∠BEC 的度数为（ ） A ．15° B ．30° C ．45° D ．60°9．如图，在等腰Rt △ABC 中斜边BC=9，从中裁剪内接正方形DEFG ，其中DE 在斜边BC 上，点F 、G 分别在直角边AC 、AB 上，按照同样的方式．．．．．在余下的三角形中继续裁剪，如此操作下A ． B ． C ． D ． A第8题 第9题B第10题第15题去，共可裁剪出边长大于1的正方形几个（ ） A ．2 B ．3 C ．4 D．5 10. 如图，下列条件：①B ACD ∠=∠；②ADC ACB ∠=∠；③AC ABCD BC=；④ AB AD AC ∙=2能单独够判定ABC ACD △∽△的个数为（ ）A ．1 个B ．2 个C ．3个D ．4个二、填空题（本题有6小题，每小题5分，共30分） 11 .函数11-=x y 中，自变量x 的取值范围是 ．12．分解因式：2327a -= ．13. 在一个不透明的袋中装有3个除颜色外其余完全相同的小球，其中白球1个，红球2个，摸出一个球后不放回．．．，再摸一个球，则两次都摸到红球的概率是 ． 14.如图，已知∠AOB=30°，M 为OB 边上一动点，以M 为圆心、2cm 为半径作⊙M 。

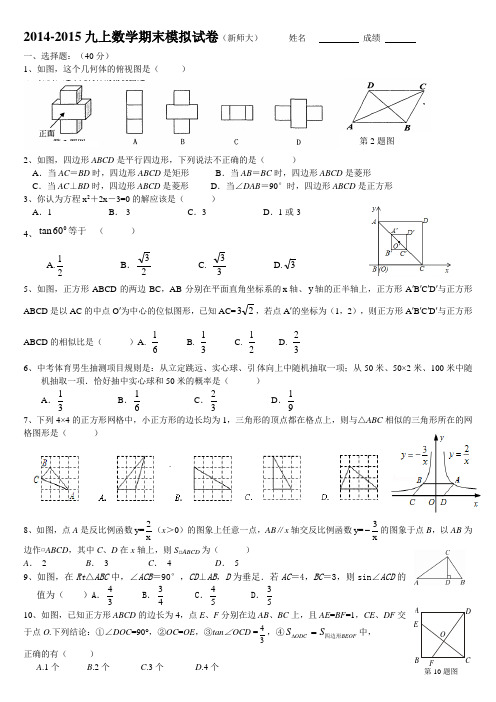
2014-2015九上数学期末模拟试卷（新师大） 姓名 成绩一、选择题：（40分）1、如图，这个几何体的俯视图是（ ）2、如图，四边形ABCD 是平行四边形，下列说法不正确的是（ ）A ．当AC ＝BD 时，四边形ABCD 是矩形B ．当AB ＝BC 时，四边形ABCD 是菱形 C ．当AC ⊥BD 时，四边形ABCD 是菱形 D ．当∠DAB ＝90°时，四边形ABCD 是正方形 3、你认为方程x 2＋2x －3=0的解应该是（ ）A ．1B ．-3C ．3D ．1或-34、060tan 等于 （ ）A.21 B ．23 C. 33 D.3 5、如图，正方形ABCD 的两边BC ，AB 分别在平面直角坐标系的x 轴、y 轴的正半轴上，正方形A ′B ′C ′D ′与正方形ABCD 是以AC 的中点O ′为中心的位似图形，已知AC=23，若点A ′的坐标为（1，2），则正方形A ′B ′C ′D ′与正方形ABCD 的相似比是（ ）A.61 B. 31 C. 21 D. 326、中考体育男生抽测项目规则是：从立定跳远、实心球、引体向上中随机抽取一项；从50米、50×2米、100米中随机抽取一项．恰好抽中实心球和50米的概率是（ ）A ．13 B ．16 C ．23 D ．197、下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC 相似的三角形所在的网格图形是（ ）8、如图，点A 是反比例函数2y=x （x ＞0）的图象上任意一点，AB ∥x 轴交反比例函数3y=x-的图象于点B ，以AB 为边作▱ABCD ，其中C 、D 在x 轴上，则S □ABCD 为（ ）A ． 2B ． 3C ． 4D ． 59、如图，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB ，D 为垂足．若AC ＝4，BC ＝3，则sin ∠ACD 的值为（ ）A ．34 B ．43 C ．54 D ．53 10、如图，已知正方形ABCD 的边长为4，点E 、F 分别在边AB 、BC 上，且AE =BF =1，CE 、DF 交于点O.下列结论：①∠DOC =90°，②OC =OE ，③tan ∠OCD =43，④ODC BEOF S S ∆=四边形中，正确的有（ ）A .1个B .2个C .3个D .4个第2题图第10题图A BC DEFO二、填空题（24分）11、计算2cos60°+ tan 245°=12、一个口袋中有10个黑球和若干个白球若干个，从口袋中随机摸出一球，记下其颜色，在把它放回摇均，重复上述过程，共实验100次，其中20次摸到黑球，于是可以估计袋中共有白球 个13、某种服装，平均每天可销售20件，每件盈利44元，若每件降价1元，则每天可多售5件，如果每天要盈利1600元，设每件降价x 元，所列的方程为 .14、如图。

七年级数学试题（时间：120分钟 满分：150分）一、选择题：（本大题共12个小题，每小题4分，共48分） 1．实数，32π，，722 39，2.0 ，8，0．1010010001，其中是无理数的有（ ） A ．2个B ．3个C ．4个D ．5个2．一个正数的平方根为2x +1和x -7，则这个正数是（ ）A ．5 B ．10 C ．25 D ．±253．下列调查中，适合用全面调查的是（ ）A .了解某班同学立定跳远的情况 B. 了解一批炮弹的杀伤半径 C .了解某种品牌奶粉中含三聚氰胺的百分比 D. 了解全国青少年喜欢的电视节目 4.已知a 、b 为实数，则下列命题正确的是（ ） A ．若b a =，则a =bB ．若a <b ,则22b a <C ．若 33b a =，则b a =;D ．若a >b ，则33b a >5、在平面直角坐标系中，点P （3，-4）位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 6．如图所示，下列条件中，能判断DE ∥AC 的是（ ）A ．EFC EDC ∠=∠B ．ACD AFE ∠=∠C ．43∠=∠D ．21∠=∠7、不等式⎩⎨⎧≥21＜x x 的解集在数轴上表示正确的是（ ）8、已知⎩⎨⎧==21y x 是关于x ，y 的方程，x -k y =3的一个解，则K 的值为（ ）A.-1 B.1 C.2 D.3 9.已知实数x ,y 满足()0122=++-y x ，则y x -等于( )A 、3B 、－3C 、1D 、－110. 已知△ABC 的三个顶点坐标分别是A(—2，3)，B(－4, －1)，C(2，0)，△ABC 中任意一点00(,)P x y 经平移后对应点为00(5,3)P x y ++，将△ABC 作同样的平移得到△111A B C ，则平移后的三个顶点坐标是（ ） A 、(3, 6)，(—1, 4)，(5, 5) B 、(3, 6)， (1, 2)， (7, 0)C 、(3, 3)， (1, 2)， (7, 3)D 、(3, 6)，(1, 2)， (7, 3) 11. 关于x 的不等式组⎩⎨⎧≤-<-1270x a x 的整数解有4个，则a 的取值范围是（ ）A.6a 7<<B. 6a 7<≤C. 6a 7≤≤D. 6a 7≤<12.如图，BD 为△ABC 角平分线，DE ∥AB ，EF 平分∠DEC ，下列结论：①∠BDE =∠FEC ；②EF ∥BD ；③CD =CE ；④BDE BDF S S ∆∆=正确的有（ ） A ．①② B ．①②③ C ．②③④ D ．①②④二、填空题：本大题共6小题，每小题4分，共24分．13.一张试卷一共有25道选择题，做对一题得4分，做错一题倒扣2分，FD AB 第12题图50cm李明同学为了得90分以上，那么他至少应做对道题14.若不等式⎩⎨⎧>-<-3212bxax的解集为－1＜x＜1，则1)1(+-ab的值为。

杭州市2015年各类高中招生文化模拟考试数学试卷参考公式：直棱柱的体积公式：V Sh =（S 为底面积，h 为高）；圆锥的全面积（表面积）公式：2S rl r ππ=+全（r 为底面半径，l 为母线长） 圆柱的全面积（表面积）公式：222S rh r ππ=+全（r 为底面半径，h 为高）一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的。

注意可以用多种不同的方法来选取正确答案。

1． 设a b .则21b a-的值为（ ）1 1 1 12． 如图是一块长、宽、高分别为6cm 、4cm 、3cm 的长方体木块，一只蚂蚁要从长方体木块的一个顶点A 处，沿着长方体的表面到长方体上和A 相对的顶点B 处吃食物，那么它需要爬行的最短路径的长是（ ）A B C D ．9cm 3． 如图，1∠的正切值为（ ）A BC ．3D ．24． 下列命题是真命题的有（ ）①对顶角相等；②两直线平行，内错角相等；③两个锐角对应相等的两个直角三角形全等；④有三个角是直角的四边形是矩形；⑤平分弦的直径垂直于弦，并且平分弦所对的弧。

A.1个B.2个C.3个D.4个5． 《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1，图2所示，图中各行从左到右列出的算筹数分别表示未知数x ，y 的系数与相应的常数项．把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来，就是3219,423.x y x y +=⎧⎨+=⎩类似地，图2所示的算筹图我们可以表述为（ ）图1 图2 A ．2114327x y x y +=⎧⎨+=⎩ B ．2114322x y x y +=⎧⎨+=⎩C ．3219423x y x y +=⎧⎨+=⎩D ．264327x y x y +=⎧⎨+=⎩6． 若不等式27125ax x x +->+对11a -≤≤恒成立，则x 的取值范围是（ ）A. 23x ≤≤B. 11x -<<C. 11x -≤≤D. 23x << 7． 一同学在n 天假期中观察：（1）下了7次雨，在上午或下午； （2）当下午下雨时，上午是晴天； （3）一共有5个下午是晴天； （4）一共有6个上午是晴天。

2014—2015学年度第二学期综合测试九年级数学参考答案一、选择题（本题共10小题,每小题3分，共30分）：1B 、 2B 、 3C 、 4C 、 5D 、 6A ； 7B 、 8D 、 9D 、 10B二、填空题（本题共6小题，每小题4分，共24分）：11； 12、26(1)x +； 13、120； 14、12y x =- ； 15、42°； 16、4123π-三、解答题（本题共3小题，每小题6分，共18分）：17、解：原式=2(1)12(1)(1)2x x x x x x x +-⨯-++-+……………………………………………………2分 =122x x x x +-++ ……………………………………………………3分 =12x + ……………………………………………………4分……………………………………………………5分…………………………………6分（解答到此给6分）1……………………(试卷讲评时要求分母有理化至最简结果)19、解：（1）作图（略）给分说明：作对一条线段得1分，作对∠C 得1分，作对△ABC 得1分，本问满分4分。

（2）过点A 作AD ⊥BC 于点D在△ACD 中，sin sin AD AC C b β=∠=∠ ………………………………………………5分∴△ABC的面积：111sin 642222S BC AD a b β===⨯⨯⨯= ……………………6分21、（1）样本平均数是__2.6___万元； ……………………………………………………2分（2）根据样本平均数估计这个商场四月份的月营业额约为___78__万元； ………………3分(3)解：设每月营业额增长率为x ，依题意，得方程：………………………………………4分 278(1)78(1)18.72x x +-+= ……………………………………………………5分 化简，得：2-0.24=0x x + 配方，得：2+0.5)0.49x =（ 解得：120.2, 1.2x x ==-（舍去） ……………………………………………………6分 答：每月营业额增长率是20%。

2014—2015学年上学期第三次统一模拟九年级数学试卷（满分：100分，考试时间：120分钟，）一、选择题：（本大题共8小题，每小题3分，共24分） 1．－5的绝对值是（ ） A ．51 B ．5 C ．5- D ．51- 2．要使式子2+a 有意义，a 的取值范围是（ ）A ．2-<aB ．2->aC ．2-≤aD ．2-≥a3．下列运算正确的是（ ）A ．6a ÷2a ＝3aB ．22532a a a -=C ．235()a a a -⋅= D ．527a b ab += 4．如图，直线21//l l ，∠1=40°，∠2=75°，则∠3等于（ ） A ．55° B ．60° C ．65° D ．70°5．观察下列图案，既是轴对称图形又是中心对称图形的有（ ）6、不等式组31526x x ->⎧⎨⎩，≤的解集在数轴上表示正确的是（ ）7．已知三角形两边的长是3和4，第三边的长是方程035122=+-x x 的根，则该三角形的周长是A ．14B ．12C ．12或14D ．以上都不对8、如图,已知抛物线x x y 421+-=和直线x y 22=.我们约定：当x 任取一值时,x 对应的函数值分别为y 1、y 2，若y 1≠y 2，取y 1、y 2中的较小值记为M ；若y 1=y 2，记M = y 1=y 2. 下列判断： ①当x ＞2时，M =y 2； ②当x ＜0时，x 值越大，M 值越大； ③使得M 大于4的x 值不存在；④若M =2，则x = 1 .其中正确的有 ( ) A ．1个 B ．2个 C ． 3个 D ．4个第4题图A ．B ．C ．D ．二、填空题：（本大题共6小题，每小题3分，共18分）9．已知x 、y 是实数，并且096132=+-++y y x ，则2014)(xy 的值是_______10．今年参加我州中考考生总数约为107300人，这个数据用科学记数法表示为_________ 11．分解因式：=-2282b a ___________________. 12．如图，已知AB ＝AC ，∠A ＝40°，AB 的垂直平分线MN 交AC 于点D ，则∠DBC ＝ ．13．若关于x 的一元二次方程0235)1(22=+-++-m m x x m 有 一个根是0，则m 的值得____________。

七年级下册数学试题一、选择题(每小题给出四个选项中只有一个是正确的,请把你认为正确的选项选出来,并将该选项的字母代号填入下表中．每选对一个得3分,选错、不选或选出的答案多于一个均得01．若m＞－1，则下列各式中错误的．．．是（）A．6m＞－6 B．－5m＜－5 C．m+1＞0 D．1－m＜22.下列各式中,正确的是( )A.±4B.=-43．已知a＞b＞0，那么下列不等式组中无解．．的是（）A．⎩⎨⎧-><bxaxB．⎩⎨⎧-<->bxaxC．⎩⎨⎧-<>bxaxD．⎩⎨⎧<->bxax4．一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度可能为（）(A) 先右转50°，后右转40° (B) 先右转50°，后左转40°(C) 先右转50°，后左转130° (D) 先右转50°，后左转50°5．解为12xy=⎧⎨=⎩的方程组是（）A.135x yx y-=⎧⎨+=⎩B.135x yx y-=-⎧⎨+=-⎩C.331x yx y-=⎧⎨-=⎩D.2335x yx y-=-⎧⎨+=⎩6．如图，在△ABC中，∠ABC=500，∠ACB=800，BP平分∠ABC，CP平分∠ACB，则∠BPC的大小是（）A．1000 B．1100 C．1150 D．1200PBA(1) (2) (3)7．四条线段的长分别为3，4，5，7，则它们首尾相连可以组成不同的三角形的个数是（）A．4 B．3 C．2 D．18．在各个内角都相等的多边形中，一个外角等于一个内角的12，则这个多边形的边数是（）A．5 B．6 C．7 D．89．如图，△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的，若△ABC的面积为20 cm2，则四边形A1DCC1的面积为（）C1A1A ．10 cm 2B ．12 cm 2C ．15 cm 2D ．17 cm 210.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(•0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )A.(5,4)B.(4,5)C.(3,4)D.(4,3)二、填空题：本大题共8个小题，每小题3分，共24分，把答案直接填在答题卷的横线上． 11.49的平方根是________,算术平方根是______,-8的立方根是_____. 12.不等式5x-9≤3(x+1)的解集是________.13.如果点P(a,2)在第二象限,那么点Q(-3,a)在_______.14.如图3所示,在铁路旁边有一李庄,现要建一火车站,•为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:____________.15.从A 沿北偏东60°的方向行驶到B,再从B 沿南偏西20°的方向行驶到C,•则∠ABC=_______度.16.如图,AD ∥BC,∠D=100°,CA 平分∠BCD,则∠DAC=_______.17．给出下列正多边形：① 正三角形；② 正方形；③ 正六边形；④ 正八边形．用上述正多边形中的一种能够辅满地面的是_____________．(将所有答案的序号都填上) 18.若│x 2-25│则x=_______,y=_______.三、解答题：本大题共7个小题，共46分，解答题应写出文字说明、证明过程或演算步骤．19．解不等式组：⎪⎩⎪⎨⎧+<-≥--.21512,4)2(3x x x x ,并把解集在数轴上表示出来．20．解方程组：2313424()3(2)17x y x y x y ⎧-=⎪⎨⎪--+=⎩C B A D21.如图, AD ∥BC , AD 平分∠EAC,你能确定∠B 与∠C 的数量关系吗?请说明理由。