相似三角形常用模型及应用

初中数学 ︵ 九年级 ︶培优篇初中数学 ︵ 九年级 ︶培优篇【基本模型】①如图，在ABC 中，点D 在AB 上，点E 在AC 上，//DEBC ，则ADE ABC △△∽，AD AE DEAB AC BC．②模型拓展1：斜交A 字型条件：C ADE ，图2结论：~ADE ACB ；③模型拓展2： 如图，∠ACD ＝∠B ⇔△ADC ∽△ACB ⇔AD AC CDAC AB BC．初中数学 ︵ 九年级︶培优篇【例1】如图，王华晚上由路灯A 下的B 处走到C 处时，测得影子CD 的长为1米，继续往前走2米到达B 处时，测得影子EF 的长为2米，已知王华的身高是1.5米，那么路灯A 的高度等于_________．【变式1-1】有一块直角三角形木板，∠B ＝90°，AB ＝1.5m ，BC ＝2m ，要把它加工成一个面积尽可能大的正方形桌面．甲、乙两位同学的加工方法分别如图1、图2所示．请你用学过的知识说明哪位同学的加工方法更好（加工损耗忽略不计）．初中数学 ︵ 九年级 ︶培优篇 【变式1-2】（2022•衢州二模）已知菱形ABCD ，E 是BC 边上一点，连接AE 交BD 于点F （1）如图1，当E 是BC 中点时，求证：AF ＝2EF ；（2）如图2，连接CF ，若AB ＝5，BD ＝8，当△CEF 为直角三角形时，求BE 的长； （3）如图3，当∠ABC ＝90°时，过点C 作CG ⊥AE 交AE 的延长线于点G ，连接DG ，若BE ＝BF ，求tan ∠BDG 的值．初中数学 ︵九年级 ︶培优篇 ③模型拓展：如图，∠A ＝∠C ⇔△AJB∽△CJD ⇔A B JA C D JC【例2】如图，在平行四边形ABCD 中，E 为边AD 的中点，连接AC 、BE 交于点F ．若△AEF 的面积为2，则△ABC 的面积为（ ） A ．8B ．10C ．12D ．14初中数学 ︵ 九年级 ︶培优篇 【变式2-1】如图，在△ABC 中，BC ＝6，AEA F EBFC，动点P 在射线EF 上，BP 交CE 于点D ，∠CBP 的平分线交CE 于点Q ，当CQ ＝14CE 时，EP ＋BP 的值为（ ）A ．9B ．12C ．18D ．24【变式2-2】如图，在Rt △ACB 中，∠ACB =90°，AC =4，BC =3，点D 为AC 上一点，连接BD ，E 为AB 上一点，CE ⊥BD 于点F ，当AD =CD 时，求CE 的长．【变式2-3】如图，已知D 是BC 的中点，M 是AD的中点．求AN:NC的值．初中数学 ︵ 九年级︶培优篇【例3】如图，在平行四边形ABCD 中，∠ABC 的平分线交AC 于点E ，交AD 于点F ，交CD 的延长线于点G ，若AF ＝2FD ，则BEEG的值为（ ） A ．12B ．13C ．23D ．34【变式3-1】（2020•杭州）如图，在正方形ABCD 中，点E 在BC 边上，连接AE ，∠DAE 的平分线AG 与CD 边交于点G ，与BC 的延长线交于点F ．设＝λ（λ＞0）．（1）若AB ＝2，λ＝1，求线段CF 的长． （2）连接EG ，若EG ⊥AF ， ①求证：点G 为CD 边的中点． ②求λ的值．初中数学 ︵ 九年级 ︶培优篇【例4】如图，在△ABC 中，45ABC ，AB A D A E ，D A E 90 ，C E，则CD 的长为______．初中数学 ︵ 九年级 ︶培优篇 【变式4-1】矩形ABCD 中，AD ＝9，AB ＝12，点E 在对角线BD 上（不与B 、D 重合），EF ⊥AE 交CD 于F 点，连接AF 交BD 于G 点． （1）如图1，当G 为DE 中点时． ①求证：FD ＝FE ； ②求BE 的长．（2）如图2，若E 为BD 上任意点，求证：AG 2＝BG •GE ．初中数学 ︵ 九年级 ︶培优篇 【变式4-2】如图，ABC 中，,,AB AC AB AC 点D E 、分别是BC AC 、的中点，AF BE ⊥与点F ．（1）求证：2AE FE BE ；（2）求A F C 的大小；（3）若DF=1，求△ABF 的面积．初中数学 ︵ 九年级 ︶培优篇结论：AH ⊥GF ，△AGF ∽△ABC ，GF AHBC AM【例5】如图1，在△ABC 中，AB =AC =5，BC =6，正方形DEFG 的顶点D 、G 分别在AB 、AC 上，EF 在BC 上． （1）求正方形DEFG 的边长；（2）如图2，在BC 边上放两个小正方形DEFG 、FGMN ，则DE= ．初中数学 ︵ 九年级 ︶培优篇 【变式5-1】有一块锐角三角形卡纸余料ABC ，它的边BC ＝120cm ，高AD ＝80cm ，为使卡纸余料得到充分利用，现把它裁剪成一个邻边之比为2：5的矩形纸片EFGH 和正方形纸片PMNQ ，裁剪时，矩形纸片的较长边在BC 上，正方形纸片一边在矩形纸片的较长边EH 上，其余顶点均分别在AB ，AC 上，具体裁剪方式如图所示． （1）求矩形纸片较长边EH 的长；（2）裁剪正方形纸片时，小聪同学是按以下方法进行裁剪的：先沿着剩余料△AEH 中与边EH 平行的中位线剪一刀，再沿过该中位线两端点向边EH 所作的垂线剪两刀，请你通过计算，判断小聪的剪法是否正确．初中数学 ︵ 九年级︶培优篇 ②拓展：（1）在正方形、长方形中经常会出现射影定理模型，如图，在有射影定理模型．（2）如图，在圆中也会出现射影定理模型．【例6】如图，四边形ABCD 中，AD ∥BC ，∠B ＝90°，E 为AB 上一点，分别以ED 、EC 为折痕将两个角(∠A 、∠B )向内折起，点A 、B 恰好落在CD 边的点F 处，若AD ＝3，BC ＝5，则EF 的长是（ ） A.15B ．215C ．17D ．217初中数学 ︵ 九年级 ︶培优篇 【变式6-1】如图所示，在△ABC 中，∠ABC ＝90°，BD ⊥AC ，DE ⊥BC ，垂足分别为D 、E 两点，则图中与△ABC 相似的三角形有（ ） A ．4个B ．3个C ．2个D ．1个【变式6-2】如图，在R t △ABC 中，∠ACB ＝90°，点D 在AB 上，且AD AC ＝ACAB． （1）求证 △ACD ∽△ABC ；（2）若AD ＝3，BD ＝2，求CD 的长．【变式6-3】ABC 中，90ABC ，BD AC ，点E 为B D 的中点，连接A E 并延长交B C 于点F ，且有AF CF ，过F 点作FH AC 于点H ． （1）求证：AD E CD B ∽； （2）求证：=2A E EF ； （3）若FHB C 的长．初中数学 ︵ 九年级 ︶培优篇②如图所示，BDE 和ABC 则ABD CBE ∽△△，且相似比为总结：旋转相似型中由公共旋转顶点、一点及其旋转后的对应点组成的三角形与由公共旋转顶点、另一点及其旋转后的对应点组成的三角形相似．初中数学 ︵ 九年级 ︶培优篇【例7】如图，在△ABC 与△ADE 中，∠ACB ＝∠AED ＝90°，∠ABC ＝∠ADE ，连接BD 、CE ，若AC ：BC ＝3：4，则BD ：CE 为（ ） A ．5：3B ．4：3C ．√5：2D ．2：√3【变式7-1】如图，点E 是菱形ABCD 对角线CA 的延长线上任意一点，以线段AE 为边作一个菱形AEFG ，且菱形AEFG ∽菱形ABCD ，相似比是：2，连接EB ，GD ．（1）求证：EB ＝GD ；（2）若∠DAB ＝60°，AB ＝2，求GD 的长．初中数学 ︵ 九年级 ︶培优篇 【变式7-2】如图，正方形ABCD ，对角线AC ，BD 相交于O ，Q 为线段DB 上的一点，90MQN ，点M 、N 分别在直线BC 、DC 上．（1）如图1，当Q 为线段OD 的中点时，求证：1132DN BM BC ；（2）如图2，当Q 为线段OB 的中点，点N 在CD 的延长线上时，则线段DN 、BM 、BC 的数量关系为 ；（3）在（2）的条件下，连接MN ，交AD 、BD 于点E 、F ，若:3:1M B M C ，N Q ，求EF 的长．初中数学 ︵ 九年级 ︶培优篇 补充：其他常见的一线三等角图形【例8】【感知】如图①，在四边形ABCD 中，点P 在边AB 上（点P 不与点A 、B 重合），90A B DPC ．易证DAP PBC △△∽．（不需要证明） 【探究】如图②，在四边形ABCD 中，点P 在边AB 上（点P 不与点A 、B 重合），A B D PC ．若4PD ，8P C ，6BC ，求AP 的长．【拓展】如图③，在ABC 中，8AC BC ，12A B ，点P 在边AB 上（点P 不与点A 、B 重合），连结CP ，作CPE A ，PE 与边BC 交于点E ，当CPE △是等腰三角形时，直接写出AP 的长．初中数学 ︵ 九年级 ︶培优篇 【变式8-1】如图，在矩形ABCD 中，CD ＝4，E 是BC 的中点，连接AE ，tan ∠AEB 43，P 是AD 边上一动点，沿过点P 的直线将矩形折叠，使点D 落在AE 上的点D ¢处，当A P D △是直角三角形时，PD 的值为（ ）A ．23或67B ．83或247C ．83或307D ．103或187初中数学 ︵ 九年级 ︶培优篇 【变式8-2】（2022秋•温州校级月考） 【推理】如图1，在正方形ABCD 中，点E 是CD 上一动点，将正方形沿着BE 折叠，点C 落在点F 处，连结BE ，CF ，延长CF 交AD 于点G ． （1）求证：BCE CDG △△≌． 【运用】（2）如图2，在【推理】条件下，延长BF 交AD 于点H ．若45HD HF ，9C E ，求线段DE 的长．【拓展】（3）将正方形改成矩形，同样沿着BE 折叠，连结CF ，延长CF ，BF 交直线AD 于G ，两点，若AB k BC ，45HD HF ，求DEEC的值（用含k 的代数式表示）．。

相似三角形模型总结相似三角形是中学数学中常见的一个概念。

相似三角形有着非常重要的应用，尤其在建筑、地图、航空等领域中被广泛地运用。

在这篇文章中，我将对相似三角形的模型及其应用进行总结。

一、相似三角形的定义相似三角形是指形状相似而大小不同的两个或多个三角形。

它们的对应角度相等，对应边的比例相等。

根据这个定义，我们可以推出相似三角形的判定定理：若两个三角形对应角度分别相等，则它们是相似的。

二、重心模型重心模型是一种抽象的几何模型，它是在研究固体对象的重心和转动惯量时得出的。

对于任意三角形 ABC，以其三条边的中点为顶点，连上互相垂直的直线，将它们相交于 G 点。

这里 G 点称为三角形 ABC 的重心，它与每个中点连成的线段相等。

同时，可以证明如果一个点在三角形内部且到三边距离的乘积等于其到三条中线距离的乘积，则该点一定是三角形的重心。

三、海龟图模型海龟图模型是一个很著名的相似三角形应用模型，它是由美国数学家T. N. Thiele 提出的。

在海龟图中，一个三角形符号代表前进一步，一个圆点符号则代表不动。

当这个图形以相似的规律继续扩展时，就能在图形中看到似乎随机且自相似的模式。

在实际操作中，我们可以将这个模型用于分形的制作和操作中，实现较好的效果。

四、印章模型印章模型是相似三角形的另一种应用模型。

在制作印章时，多会使用到相似三角形的概念。

根据相似三角形的定义，我们可以通过相似三角形来制造缩小复制的图案。

具体来说，我们可以通过将大三角形分割为单位面积相等的若干小三角形，然后根据相似的规律进行缩小，就可以得到与大三角形相似而更小的三角形。

五、三角剖分模型三角剖分模型是相似三角形的一种实际应用模型。

在三角剖分中，我们会把一个多边形分解为多个三角形，这些三角形可以保持相似性，这比将多边形分解成其它形状的图形更容易实现。

总结在本文中，我们总结了几种相似三角形的应用模型，这些模型不仅具有学术研究的意义，更能够应用于实际的生产和生活中。

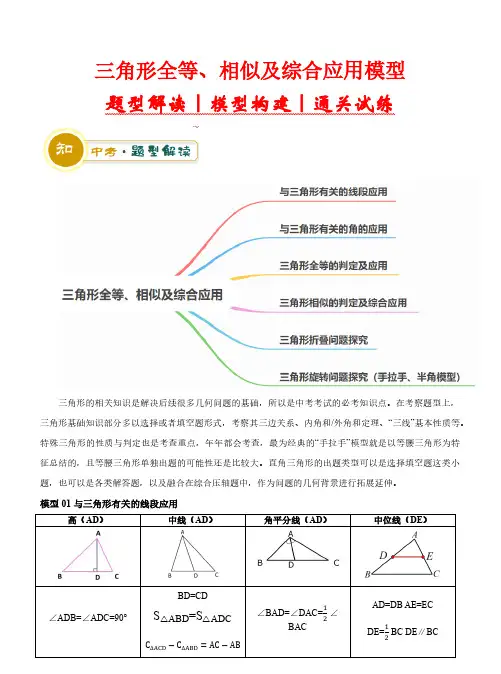
三角形全等、相似及综合应用模型题型解读｜模型构建｜通关试练三角形基础知识部分多以选择或者填空题形式，考察其三边关系、内角和/外角和定理、“三线”基本性质等。

特殊三角形的性质与判定也是考查重点，年年都会考查，最为经典的“手拉手”模型就是以等腰三角形为特征总结的，且等腰三角形单独出题的可能性还是比较大。

直角三角形的出题类型可以是选择填空题这类小题，也可以是各类解答题，以及融合在综合压轴题中，作为问题的几何背景进行拓展延伸。

模型01 与三角形有关的线段应用高（AD）中线（AD）角平分线（AD）中位线（DE）模型02 与三角形有关的角的应用（1）三角形的内角：（1）三角形内角的概念：三角形内角是三角形三边的夹角．每个三角形都有三个内角，且每个内角均大于0°且小于180°．（2）三角形内角和定理：三角形内角和是180°．（3）三角形内角和定理的证明证明方法，不唯一，但其思路都是设法将三角形的三个内角移到一起，组合成一个平角．在转化中借助平行线．（4）三角形内角和定理的应用主要用在求三角形中角的度数．①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．（2）三角形的外角：（1）三角形外角的定义：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．三角形共有六个外角，其中有公共顶点的两个相等，因此共有三对．（2）三角形的外角性质：①三角形的外角和为360°．②三角形的一个外角等于和它不相邻的两个内角的和．③三角形的一个外角大于和它不相邻的任何一个内角．（3）若研究的角比较多，要设法利用三角形的外角性质②将它们转化到一个三角形中去．（4）探究角度之间的不等关系，多用外角的性质③，先从最大角开始，观察它是哪个三角形的外角．模型03 三角形全等的判定及应用（1）全等三角形的定义：全等的图形必须满足：（1）形状相同；（2）大小相等能够完全重合的两个三角形叫做全等三角形。

相似三角形12种基本模型证明相似三角形是指拥有相同形状但不同大小的三角形。

在三角形中，如果它们的对应角度相等，那么它们就是相似三角形。

相似三角形一般用比例关系表示。

下面是相似三角形12种基本模型的证明：1. AAA相似模型如果两个三角形的三个角分别相等，则它们是相似的。

证明：三角形的三个角之和为180度。

如果两个三角形的三个角分别相等，那么它们的三个角和也相等，即这两个三角形的三个角和相等，因此它们是相似的。

2. AA相似模型如果两个三角形中有两个对应角相等，则它们是相似的。

证明：假设两个三角形的对应角分别为A和A’，B和B’，C和C’。

由于A和A’相等，B和B’相等，那么它们的第三个对应角C和C’也必须相等。

因此，这两个三角形的三个角分别相等，它们是相似的。

3. SSS相似模型如果两个三角形的三条边分别成比例，则它们是相似的。

证明：假设两个三角形的三条边为a, b, c和a’, b’, c’。

由于它们是成比例的，即a/a’= b/b’= c/c’，那么它们的三边比例相等，即它们是相似的。

4. SAS相似模型如果两个三角形中有两条边成比例，且夹角相等，则它们是相似的。

证明：假设两个三角形的两条边为a, b和a’, b’，夹角为C和C’。

由于它们是成比例的，即a/a’= b/b’，那么它们的三边比例相等。

又由于它们的夹角相等，即C = C’，因此它们是相似的。

5. ASA相似模型如果两个三角形中有两个角相等，且它们对应的两条边成比例，则它们是相似的。

证明：假设两个三角形的两个对应角分别为A和A’，B和B’，且对应的两条边分别为a, a’和b, b’。

由于它们的两条边成比例，即a/a’= b/b’，那么它们的三边比例相等。

又由于它们的两个角相等，即A = A’，因此它们是相似的。

6. HL相似模型如果两个三角形中有一条边和一条斜边分别成比例，且这两条边夹角相等，则它们是相似的。

证明：假设两个三角形的一条边为b，斜边为c，且夹角为C，另一个三角形的一条边为b’，斜边为c’，且夹角为C’。

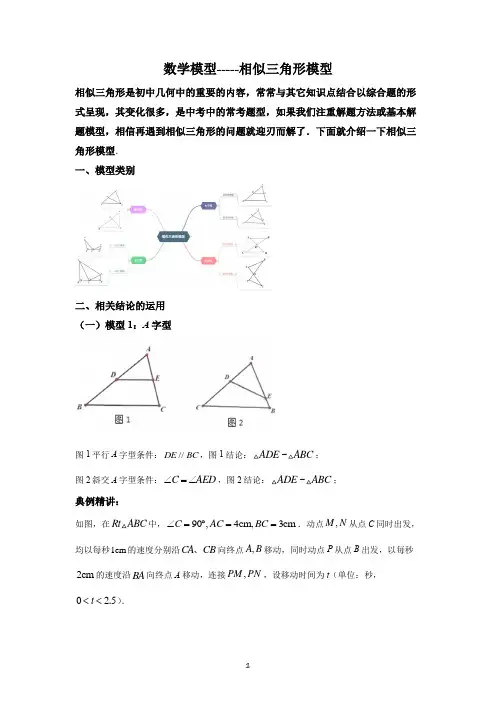
数学模型-----相似三角形模型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考中的常考题型，如果我们注重解题方法或基本解题模型，相信再遇到相似三角形的问题就迎刃而解了．下面就介绍一下相似三角形模型． 一、模型类别二、相关结论的运用 （一）模型1：A 字型图1平行A 字型条件：//DE BC ，图1结论：~ADE ABC ； 图2斜交A 字型条件：C AED ∠=∠，图2结论：~ADE ABC ；典例精讲：如图，在Rt ABC 中，90,4cm,3cm C AC BC ∠=︒==．动点,M N 从点C 同时出发，均以每秒1cm 的速度分别沿CA CB 、向终点,A B 移动，同时动点P 从点B 出发，以每秒2cm 的速度沿BA 向终点A 移动，连接,PM PN ，设移动时间为t （单位：秒，025t <<．）．（1）当t 为何值时，以,,A P M 为顶点的三角形与ABC 相似？（2）是否存在某一时刻t ，使四边形APNC 的面积S 有最小值？若存在，求S 的最小值；若不存在，请说明理由． 【思路点拨】根据勾股定理求得5cm AB =．（1）根据模型1：平行A 字型的结论得出APM ABC ∽，和模型1：斜交A 字型模型的结论得出AMP ABC ∽两种情况讨论：利用相似三角形的对应边成比例来求t 的值． （2）过点P 作PH BC ⊥于点H ，构造平行线//PH AC ，根据模型1：平行A 字型的结论得出PBH ABC ∽，从而求得以t 表示的PH 的值；然后根据“ABCBPHSSS=-”列出S 与t 的关系式24321(0 2.5)525S t t ⎛⎫=-+<< ⎪⎝⎭，则由二次函数最值的求法即可得到S的最小值． 【详解】解：∵如图，在Rt ABC 中，90,4cm,3cm C AC BC ∠=︒==．∴根据勾股定理，得5cm AB ==．（1）以,,A P M 为顶点的三角形与ABC 相似，分两种情况： ①当APM ABC ∽时，AM AP AC AB =，即45245t t--=，解得0t =（不合题意，舍去）．②当AMP ABC ∽时，AP AM AC AB =，即52445t t --=，解得32t =；综上所述，当32t =时，以A P M 、、为顶点三角形与ABC 相似．（2）存在某一时刻t ，使四边形APNC 的面积S 有最小值．理由如下： 假设存在某一时刻t ，使四边形APNC 的面积S 有最小值． 如图，过点P 作PH BC ⊥于点H ．则//PH AC ， ∴PBH ABC ∽∴PH BPAC BA =， 即245PH t=． ∴85tPH =． ∴ABC BPN S S S =-△△()118343225t t =⨯⨯-⨯-⋅ ()24321=0 2.5525t t ⎛⎫-+<< ⎪⎝⎭． ∵405>， ∴S 有最小值． 当32t =时，215S =最小值．答：当32t =时，四边形A P NC 的面积S 有最小值，其最小值是215． 【解题技法】作平行线构造A 字型相似，是解题中常用的一种作辅助线的方法实战演练：1. 如图，AD经过ABC的重心，点E是AC的中点，过点E作//EG BC交AD 于点G，若12BC=，则线段GE的长为（）A. 6B. 4C. 5D. 3【答案】D【解析】【分析】根据重心的概念得到点D为BC中点，即CD的长，再根据平行证明△AGE∽△ADC，结合点E是AC中点，得到12AE GEAC CD==，从而求出GE.【详解】解：∵AD经过ABC的重心，∴点D是BC中点，∵BC=12，∴CD=BD=6，∵GE∥BC，∴△AGE∽△ADC，∵点E是AC中点，∴12AE GEAC CD==，即162GE=，解得：GE=3，故选D.【点睛】本题考查的是重心的概念和性质、相似三角形的判定和性质，掌握三角形的重心是三角形三条中线的交点是解题的关键.2. 如图，在ABC 中，//DE BC ，//EF AB ，则下列结论正确的是（ ）A.AD DEDB BC= B.BF EFBC AD= C.EF BFAB BC= D.AE DEEC FC= 【答案】D 【解析】【分析】由两直线平行，得到两对同位角相等，证明△ADE ∽△ABC ，△CEF ∽△CAB ；由等代换可证明△ADE ～△EFC ，最后由相似三角形的性质判断四个答案的正误． 【详解】解：∵DE ∥BC ， ∴∠ADE=∠B ，∠AED=∠C ， ∴△ADE ∽△ABC ，DE AD ADBC AB DB∴=≠ ∴答案A 错舍去； 又∵EF ∥AB ，∴∠CEF=∠A ，∠CFE=∠B ， ∴△CEF ∽△CAB ，EF CE FC BFAB AC BC BC∴==≠ ∴答案C 错舍去； ∵//DE BC ，//EF AB ， ∴四边形BDEF 是平行四边形，∴DE=BF∵∠ADE=∠B ，∠CFE=∠B ， ∴∠ADE=∠CFE ， 又∵∠AED=∠C ， ∴△ADE ～△EFC ，EF BF BFAD FC D B E FC C∴==≠ ∴答案B 舍去 ∵△ADE ～△EFC ，AE DEEC FC∴= ∴答案D 正确； 故选：D ．【点睛】本题考查了平行线的性质，相似三角形的判定与性质，平行四边形的判定与性质等知识点，重点掌握三角形相似的判定与性质，易错点学生不会找两个相似三角形对应边的比相等．3. 如图，在ABC 中，D 、E 分别在AB 边和AC 边上，//DE BC ，M 为BC 边上一点（不与B 、C 重合），连结AM 交DE 于点N ，则（ ）A.ADANAN AEB.BD MNMN CEC.DN NEBM MCD.DN NEMC BM【答案】C 【解析】【分析】根据平行线的性质和相似三角形的判定可得△ADN ∽△ABM ，△ANE ∽△AMC ，再根据相似三角形的性质即可得到答案.【详解】∵//DE BC ，∴△ADN ∽△ABM ，△ANE ∽△AMC ，∴,DN AN ANNE DN NEBMAM AM MC BM MC，故选C.【点睛】本题考查平行线的性质、相似三角形的判定和性质，解题的关键是熟练掌握平行线的性质、相似三角形的判定和性质.（二）模型2：8字型图1平行8字型条件：//AB CD ， 图1结论：AOB DOC ∽△△； 图2斜交8字型条件：A D ∠=∠，，图2结论：AOB DOC ∽△△；典例精讲：如图1，在矩形ABCO 中，8,6,,OA OC D E ==分别是,AB BC 上一点，2,3,AD CE OE ==与CD 相交于点F ．（1）求证：OE CD ⊥；（2）如图2，点G 是CD 的中点，延长OG 交BC 于H ，求CH 的长． 【思路点拨】（1）根据四边形ABCO 是矩形，可得8,6OA BC OC AB ====，根据模型1中的图1结论得出ADP OCP ∽，从而求出PA 和PO ，再根据模型2中的图1结论得出OPF ECF ∽，求出EF 和CF 的长，再根据勾股定理的逆定理即可得OE CD ⊥；（2）在Rt CBD △中，8,624CB BD AB AD ==-=-=，根据勾股定理可得CD =G 是CD 的中点，可得CG DG ==G 是CP 的三等分点，根据模型2中的图1结论得出OPG HCG ∽即可求出CH 的长． 【详解】（1）∵四边形ABCO 是矩形， ∴8,6OA BC OC AB ====， 在Rt OCE 中，3CE =，∴OE ===∵//AB OC ，即//AD OC ，且2AD =， ∴ADP OCP ∽ ∴AD PAOC PO =， ∴268PA PA =+， ∴4PA =，∴12PO PA OA =+=， ∴在Rt OPC △中，6OC =，∴CP ===，∵//OA BC ，即//OP CE ， ∴OPF ECF ∽ ∴CE EF CFOP OF PF ==， ∴31124EF CF OF PF ===，∴15EF OE ==155CF CP ==∵22936955+=+=⎝⎭⎝⎭， ∴222EF CF CE +=， ∴CEF △是直角三角形， ∴90CFE ∠=︒， ∴OE CD ⊥；（2）在Rt CBD △中，8,624CB BD AB AD ==-=-=，根据勾股定理，得CD ===，∵点G 是CD 的中点，∴CGDG ==由（1）知：CP =，∴DP CP CD =-=∴点G 是CP 的三等分点， ∵//OA BC ，即//OP CH ， ∴APG HCG ∽ ∴CH CGOP GP=， ∴1122CH =， ∴6CH =． 答：CH 的长为6．【解题技法】利用A 字型和8字型混合模型得出三角形相似，再利用相似三角形的对应边成比例得出线段的长或比值，解决本题的关键实战演练：4. 已知，如图，在平行四边形ABCD 中，M 是BC 边的中点，E 是边BA 延长线上的一点，连接EM ，分别交线段AD 于点F 、AC 于点G ．（1）证明：AFG ∆∽CMG ∆ （2）求证：GF EFGM EM=； 【答案】（1）详见解析；（2）详见解析． 【解析】【分析】（1）利用平行线的性质及对顶角相等即可证明AFG ∆∽CMG ∆；（2）由相似三角形的性质可知GF AF GM CM=，由AD∽BC 可知AF EFBM EM =，通过等量代换即可证明结论． 【详解】（1）证明：AD ∥BCFAG MCG ∴∠=∠ AGF CGM ∠=∠ AFG ∴∆∽CMG ∆（2）证明：∵AFG ∆∽CMG ∆GF AFGM CM∴= ∽AD∽BC ， ∽AF EFBM EM= 又∵CM ＝BM ，AF EFCM EM∴=GF EFGM EM∴=【点睛】本题主要考查相似三角形的判定及性质，掌握相似三角形的判定方法及性质是解题的关键．5. 如图，在平行四边形ABCD中，点E在边BC上，连结AE并延长，交对角线BD于点F、DC的延长线于点G．如果23CEBE=，求FEEG的值．【答案】916 FEEG=【解析】【分析】由四边形ABCD是平行四边形，可得AD=BC，AD∥BC，即可证得△ADF∽△EBF，△GEC∽△GAD，然后由相似三角形的对应边成比例，求得答案．【详解】∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴△ADF∽△EBF，△GEC∽△GAD，∴EF BE EG ECAF AD AG AD＝，＝，∵23 CEBE=，∴3255 BE CEAD AD＝，＝，∴3255FE EGAF AG==，，∴3283FE EGAE AE==，，∴916FEEG=．【点睛】此题考查相似三角形的判定与性质以及平行四边形的性质．解题关键在于注意掌握数形结合思想的应用．6. 如图， ,BD AC 相交于点P ，连结,,,,AB BC CD DA DAP CBP ∠=∠． (1)求证: ADP BCP ∽；(2)直接回答ADP △与BCP 是不是位似图形? (3)若8,4,3AB CD DP ===，求AP 的长．【答案】（1）详见解析；（2）不是；（3）6AP = 【解析】【分析】（1）根据已知条件可知DAP CBP ∠=∠，根据对顶角相等可知DPA CPB ∠=∠，由此可证明ADP BCP ∽；（2）根据位似图形的定义（如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．）（3）由△ADP ∽△BCP ，可得AP BPDP CP=，而∠APB 与∠DPC 为对顶角，则可证△APB ∽△DPC ，从而得AP ABDP DC=，再根据8,4,3AB CD DP ===即可求得AP 的长．【详解】(1)证明:∵,DAP CBP DPA CPB ∠=∠∠=∠， ∴ADP BCP ∽；(2)点A 、D 、P 的对应点依次为点B 、C 、P ，对应点的连线不相交于一点，故ADP △与BCP 不是位似图形；(3)解:∵ADP BCP ∽ ∴=AP BP DP CP∵APB DPC ∠=∠，∴APB DPC ∽，AP ABDP DC∴= ∴8=43AP ∴6AP =．【点睛】本题考查相似三角形的性质和判定，位似图形的定义．熟练掌握相似三角形的判定定理是解决此题的关键．7. 在△ABC 中，90ACB ∠=，BE 是AC 边上的中线，点D 在射线BC 上．（1）如图1，点D 在BC 边上，:1:2CD BD =，AD 与BE 相交于点P ，过点A 作AFBC ，交BE 的延长线于点F ，易得APPD的值为 ； （2）如图2，在△ABC 中，90ACB ∠=，点D 在BC 的延长线上，AD 与AC 边上的中线BE 的延长线交于点P ，:1:2DC BC =，求APPD的值； （3）在（2）的条件下，若CD=2，AC=6，则BP= ． 【答案】（1）32；（2）23；（3）6【解析】【分析】（1）易证△AEF ≌△CEB ，则有AF=BC ．设CD=k ，则DB=2k ，AF=BC=3k ，由AF ∥BC 可得△APF ∽△DPB ，然后根据相似三角形的性质就可求出APPD的值；（2）过点A 作AF ∥DB ，交BE 的延长线于点F ，设DC=k ，由DC ：BC=1：2得BC=2k，DB=DC+BC=3k．易证△AEF≌△CEB，则有EF=BE，AF=BC=2k．易证△AFP∽△DBP，然后根据相似三角形的性质就可求出APPD的值；（3）当CD=2时，可依次求出BC、AC、EC、EB、EF、BF的值，然后根据FP BP的值求出BFBP的值，就可求出BP的值．【详解】解：（1）如图1中，∵AF∥BC，∴∠F=∠EBC，∵∠AEF=∠BEC，AE=EC，∴△AEF≌△CEB（AAS），∴AF=BC．设CD=k，则DB=2k，AF=BC=3k，∵AF∥BC，∴△APF∽△DPB，∴32 PA AFPD BD==，故答案是：32；（2）如图2，过点A作AF∥DB，交BE的延长线于点F，设DC=k ，由DC ：BC=1：2得BC=2k ，DB=DC+BC=3k ． ∵E 是AC 中点， ∴AE=CE ． ∵AF ∥DB ， ∴∠F=∠1．在△AEF 和△CEB 中，123F AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△AEF ≌△CEB ， ∴EF=BE ，AF=BC=2k ． ∵AF ∥DB ， ∴△AFP ∽△DBP ， ∴2233PA FP AF k PD BP BD k ====； （3）当CD=2时，BC=4， ∵AC=6， ∴EC=AE=3， ∴EB=5=∴EF=BE=5，BF=10． ∵23FP BP =， 53BF BP ∴=， ∴BP=35BF=35×10=6．故答案为6．【点睛】本题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识，结合中点，作平行线构造全等三角形是解决本题的关键．（三）模型3：k 字型图1一线三垂直条件：,,AB BD DE BD AC CE ⊥⊥⊥，图1结论：ABC CDE ∽△△； 图2一线三等角条件：B ACE D ∠=∠=∠，图2结论：ABC CDE ∽△△；典例精讲：如图，点P 是线段BD 上一个动点，90,6,4,B D AB CD BD a ∠=∠=︒===． （1）当90,14APC a ∠=︒=时，求BP 的长度；（2）若90APC ∠=︒时，点P 有两个符合要求即12,P P ，且122PP =，求a 的值； （3）若120APC ∠=︒时，点P 有且只有一个点符合要求，求a 的值．【思路点拨】（1）根据模型3：k 字型一线三垂直，证得ABP PDC △∽△，根据相似三角形的性质即可求得；（2）设BP x =，则PD a x =-，根据模型3：k 字型的一线三垂直证得ABP PDC △∽△，由相似三角形的性质得到2240x ax -+=，设方程的两个根为12,x x ，根据根与系数的关系可知1212,24x x a x x +=⋅=，根据题意即可得到()2121244x x x x =+-=，即可得到24244a -⨯=，解得即可；（3）作120AEP CFP ∠=∠=︒，解直角三角形求得33BE DF AE CF ====，根据模型3：k 字型的一线三等角证得EPA FCP ∽，由相似三角形的性质得到2320x a x ⎛--+= ⎝⎭，根据题意241320a ⎛∆=--⨯⨯= ⎝⎭，即可即可．【详解】解：（1）∵90,90B D APC ∠=∠=︒∠=︒， ∴90A APB CPD APB ∠+∠=∠+∠=︒， ∴A CPD ∠=∠， ∴ABP PDC △∽△， ∴BP AB CD PD =，即6414BP BP=-， 解得2BP =或12；（2）设BP x =，则PD a x =-， 由（1）可知ABP PDC △∽△， ∴AB BP PD DC=，即64xa x =-， ∴2240x ax -+=，设方程的两个根为12,x x ，根据根与系数的关系可知1212,24x x a x x +=⋅=，∵122PP =， ∴122x x -=，∴()()2212121244x x x x x x -=+-=，∴24244a -⨯=， 解得10a =±（负数舍去）， ∴10a =；（3）作120AEP CFP ∠=∠=︒， ∴60AEB CFD ∠=∠=︒， ∵6,4AB CD ==，∴BE AB DF ====∴223AE BE CF DF ====∵120AEP CFP APC ∠=∠=∠=︒， ∴EAP CPF ∠=∠， ∴EPA FCP ∽， ∴AE EPPF FC=， 设EP x =，则3PF a x =--，=，∴2320x a x ⎛--+= ⎝⎭，∵0=，∴2413203a ⎛--⨯⨯= ⎝⎭， ∵0a >，∴3a =+【解题技法】通过运用模型3：k 字型中从特殊到一般的方法，证明出两组对应角相等，从而得出相似三角形，利用对应边成比例是解题的关键．实战演练：8. 如图1和图2，在ABC ∆中，AB AC =，8BC =，3tan 4C =．点K 在AC 边上，点M ，N 分别在AB ，BC 上，且2AM CN ==．点P 从点M 出发沿折线MB BN -匀速移动，到达点N 时停止；而点Q 在AC 边上随P 移动，且始终保持APQ B ∠=∠．（1）当点P 在BC 上时，求点P 与点A 的最短距离；（2）若点P 在MB 上，且PQ 将ABC ∆的面积分成上下4：5两部分时，求MP 的长；（3）设点P 移动的路程为x ，当03x ≤≤及39x ≤≤时，分别求点P 到直线AC 的距离（用含x 的式子表示）；（4）在点P 处设计并安装一扫描器，按定角APQ ∠扫描APQ ∆区域（含边界），扫描器随点P 从M 到B 再到N 共用时36秒．若94AK =，请直接．．写出点K 被扫描到的总时长．【答案】（1）3；（2）43MP =；（3）当03x ≤≤时，24482525d x =+；当39x ≤≤时，33355d x =-+；（4）23t s =【解析】【分析】（1）根据当点P 在BC 上时，PA ⊥BC 时PA 最小，即可求出答案； （2）过A 点向BC 边作垂线，交BC 于点E ，证明△APQ ∽△ABC ，可得2APQ ABCS AP S AB ∆∆⎛⎫= ⎪⎝⎭，根据S S 上下=45可得 24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭，可得23AP AB =，求出AB=5，即可解出MP ；（3）先讨论当0≤x≤3时，P 在BM 上运动，P 到AC 的距离：d=PQ ·sinC ，求解即可，再讨论当3≤x≤9时，P 在BN 上运动，BP=x-3，CP=8-（x-3）=11-x ，根据d=CP·sinC 即可得出答案； （4）先求出移动的速度=936=14，然后先求出从Q 平移到K 耗时，再求出不能被扫描的时间段即可求出时间．【详解】（1）当点P 在BC 上时，PA ⊥BC 时PA 最小， ∵AB=AC ，△ABC 为等腰三角形， ∴PA min =tanC·2BC =34×4=3； （2）过A 点向BC 边作垂线，交BC 于点E ，S 上=S △APQ ， S 下=S 四边形BPQC ， ∵APQ B ∠=∠， ∴PQ ∥BC ， ∴△APQ ∽△ABC ，∴APAQPQAB AC BC ==， ∴2APQ ABCS AP S AB ∆∆⎛⎫= ⎪⎝⎭， 当S S 上下=45时，24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭， ∴23APAB =， AE=2BC·tan 3C =，根据勾股定理可得AB=5， ∴2253APMP AB +==，解得MP=43；（3）当0≤x≤3时，P 在BM 上运动，P 到AC 的距离：d=PQ·sinC ，由（2）可知sinC=35，∴d=35PQ ，∵AP=x+2， ∴25APx PQAB BC +==，∴PQ=285x +⨯，∴d=23855x +⨯⨯=24482525x +，当3≤x≤9时，P 在BN 上运动，BP=x-3，CP=8-（x-3）=11-x ， d=CP·sinC=35（11-x ）=-35x+335，综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩； （4）AM=2<AQ=94， 移动的速度=936=14， ①从Q 平移到K ，耗时：92414-=1秒， ②P 在BC 上时，K 与Q 重合时 CQ=CK=5-94=114， ∵∠APQ+∠QPC=∠B+∠BAP ，APQ B ∠=∠∴∠QPC=∠BAP ，又∵∠B=∠C ，∴△ABP ∽△PCQ ，设BP=y ，CP=8-y ，AB BP PC CQ =，即51184y y =-， 整理得y 2-8y=554-， （y-4）2=94， 解得y 1=52，y 2=112， 52÷14=10秒， 112÷14=22秒， ∴点K 被扫描到的总时长36-（22-10）-1=23秒．【点睛】本题考查了相似三角形的判定和性质，锐角三角函数，一次函数的应用，结合知识点灵活运用是解题关键．9. 如图，△AOB是直角三角形，∠AOB＝90°，OB＝2OA，点A在反比例函数y＝1 x 的图象上．若点B在反比例函数y＝kx的图象上，则k的值为_____．【答案】-4【解析】【分析】要求函数的解析式只要求出B点的坐标就可以，过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D．根据条件得到△ACO∽△ODB，得到：BD OD OB OC AC OA==＝2，然后用待定系数法求解即可．【详解】过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D，设点A的坐标是(m，n)，则AC＝n，OC＝m．∵∠AOB＝90°，∴∠AOC+∠BOD＝90°，∵∠DBO+∠BOD＝90°，∴∠DBO＝∠AOC，∵∠BDO＝∠ACO＝90°，∴△BDO∽△OCA．∴BD OD OB OC AC OA==，∵OB ＝2OA ，∴BD ＝2m ，OD ＝2n ，因为点A 在反比例函数y ＝1x 的图象上， ∴mn ＝1，∵点B 在反比例函数y ＝k x的图象上， ∴B 点的坐标是(﹣2n ，2m)，∴k ＝﹣2n •2m ＝﹣4mn ＝﹣4，故答案为﹣4．【点睛】本题考查了反比例函数图象上点的坐标特征，相似三角形的判定和性质，利用相似三角形的性质求得点B 的坐标(用含n 的式子表示)是解题的关键． 10. 如图，在ABC 中，点D E 、分别在边BC AC 、上，连接AD DE 、，且B ADE C ∠=∠=∠．（1）证明：BDA CED △∽△；（2）若45,2B BC ∠=︒=，当点D 在BC 上运动时（点D 不与B C 、重合），且ADE 是等腰三角形，求此时BD 的长．【答案】(1)理由见详解；（2）2BD =-1，理由见详解．【解析】【分析】∽1∽根据题目已知条件易得：180ADE ADB EDC ∠+∠+∠=︒，180B ADB DAB ∠+∠+∠=︒，所以得到DAB EDC ∠=∠，问题得证．∽2∽由题意易得ABC 是等腰直角三角形，所以90BAC ∠=︒，当ADE 是等腰三角形时，根据分类讨论有三种情况：①AD=AE ，②AD=DE ，③AE=DE ；因为点D 不与B C 、重合，所以第一种情况不符合，其他两种情况根据等腰三角形的性质“等边对等角”及45B ADE ∠=∠=︒，求出问题即可．【详解】（1）如图可知：180ADE ADB EDC ∠+∠+∠=︒在ABD △中，∴ 180B ADB DAB ∠+∠+∠=︒ 又B ADE C ∠=∠=∠∴EDC DAB ∠=∠∴BDA CED △∽△．（2）B ADE C ∠=∠=∠，45B ∠=︒∴ABC 是等腰直角三角形∴90BAC ∠=︒BC=2，∴AB=AC=2 ①当AD=AE 时，∴ADE AED ∠=∠45B ∠=︒，∴=45B ADE AED ∠=∠∠=︒∴90DAE ∠=︒∴90DAE BAC ∠=∠=︒点D 在BC 上运动时（点D 不与B C 、重合）,点E 在AC 上∴此情况不符合题意．②当AD=DE 时，∴DAE DEA ∠=∠∴由（1）结论可知：BDA CED ≌∴∴2BD =③当AE=DE 时，45ADE DAE ∠=∠=︒∴AED 是等腰直角三角形45B ∠=︒，∴==45B C DAE ∠∠∠=︒∴90ADC ∠=︒，即AD BC ⊥ ∴1=12BD BC =．综上所诉：2BD =1．【点睛】本题主要考查相似三角形的判定及等腰三角形的存在性问题，关键是利用“K ”型相似模型及根据“等边对等角”、等腰直角三角形的性质得到线段的等量关系，进而求解问题．11. 感知：如图①，在四边形ABCD 中，AB ∥CD ，∠B ＝90°，点P 在BC 边上，当∠APD＝90°时，可知△ABP∽△PCD．（不要求证明）探究：如图②，在四边形ABCD中，点P在BC边上，当∠B＝∠C＝∠APD时，求证：△ABP∽△PCD．拓展：如图③，在△ABC中，点P是边BC的中点，点D、E分别在边AB、AC上．若∠B＝∠C＝∠DPE＝45°，BC＝，BD＝4，则DE的长为．【答案】探究：见解析；拓展：52.【解析】【分析】感知：先判断出∠BAP＝∠DPC，进而得出结论；探究：根据两角相等，两三角形相似，进而得出结论；拓展：利用△BDP∽△CPE得出比例式求出CE，结合三角形内角和定理证得AC⊥AB且AC＝AB；最后在直角△ADE中利用勾股定理来求DE的长度．【详解】解：感知：∵∠APD＝90°，∴∠APB+∠DPC＝90°，∵∠B＝90°，∴∠APB+∠BAP＝90°，∴∠BAP＝∠DPC，∵AB∥CD，∠B＝90°，∴∠C＝∠B＝90°，∴△ABP∽△PCD；探究：∵∠APC＝∠BAP+∠B，∠APC＝∠APD+∠CPD，∴∠BAP+∠B＝∠APD+∠CPD．∵∠B＝∠APD，∴∠BAP＝∠CPD．∵∠B＝∠C，∴△ABP∽△PCD；拓展：同探究的方法得出，△BDP ∽△CPE ， ∴BD BP CP CE=， ∵点P 是边BC 的中点，∴BP ＝CP ＝，∵BD ＝4，CE=， ∴CE ＝92， ∵∠B ＝∠C ＝45°，∴∠A ＝180°﹣∠B ﹣∠C ＝90°，即AC ⊥AB 且AC ＝AB ＝6，∴AE ＝AC ﹣CE ＝6﹣92＝32，AD ＝AB ﹣BD ＝6﹣4＝2，在Rt △ADE 中，DE 52． 故答案是：52． 【点睛】此题是相似综合题．主要考查了相似三角形的判定与性质、勾股定理、三角形内角和定理以及三角形外角的性质．解本题的关键是判断出△ABP ∽△PCD ．（四）模型4：母子型图1垂直母子型条件：,AC BC AB CD ⊥⊥，图1结论：ABC ACD CBD ∽∽； 图2斜交母子字型条件：C ABD ∠=∠，图2结论：ABC ABD ∽；典例精讲：1、在Rt ABC 中，90,ACB CD AB ∠=︒⊥，垂足为,8,2D AD DB ==，求CD 的长【思路点拨】根据垂直母子型模型4证得ADC CDB ∽△△，再根据对应边成比例，即可求出CD 的值．【详解】∵CD AB ⊥，∴90ADC CDB ∠=∠=︒，∴90ACD A ∠+∠=︒，∵90ACB ∠=︒，∴90ACD BCD ∠+∠=︒，∴A BCD ∠=∠，∴ADC CDB ∽△△， ∴CD AD BD CD=， ∴28216CD AD BD =⋅=⨯=，∴4CD =．2、如图，在ABC 中，AB AC =，点P 、D 分别是BC AC 、边上的点，且APD B ∠=∠．（1）求证：AC CD CP BP ⋅=⋅；（2）若10,12AB BC ==，当//PD AB 时，求BP 的长．【思路点拨】（1）根据已知得出APD B C ∠=∠=∠，再根据斜交母子型模型4得出ABP PCD ∽，根据相似三角形的性质得到AB CD CP BP ⋅=⋅，由AB AC =即可得到AC CD CP BP ⋅=⋅；（2）由//PD AB 根据斜交母子型模型4得出BAP BCA ∽，然后运用相似三角形的性质即可求出BP 的长．【详解】（1）∵AB AC =，∴B C ∠=∠．∵APD B ∠=∠，∴APD B C ∠=∠=∠．∵,APC BAP B APC APD DPC ∠=∠+∠∠=∠+∠，∴BAP DPC ∠=∠，∴ABP PCD ∽， ∴BP AB CD CP=， ∴AB CD CP BP ⋅=⋅．∵AB AC =，∴AC CD CP BP ⋅=⋅；（2）如图，∵//PD AB ，∴APD BAP ∠=∠．∵APD C ∠=∠，∴BAP C ∠=∠．∵B B ∠=∠，∴BAP BCA ∽， ∴BA BP BC BA=． ∵10,12AB BC ==， ∴101210BP =， ∴253BP =．【解题技法】利用母子型模型4中有一组隐含的等角，此时需要通过已知得出判定三角形相似的条件，把证明AC CD CP BP ⋅=⋅转化为证明AB CD CP BP ⋅=⋅是解题的关键． 实战演练：12. 如图，已知BC 是O 的直径，AC 切O 于点C ，AB 交O 于点D ，E 为AC 的中点，连接CD ，DE ．（1）求证：DE 是O 的切线；（2）若4BD =，3CD =，求AC 的长．【答案】（1）见解析；（2）154=AC ． 【解析】 【分析】（1）连接OD ，根据切线的性质和直角三角形斜边的中线以及等腰三角形的性质得出，EDC ECD ∠=∠，ODC OCD ∠=∠，然后利用等量代换即可得出DE OD ⊥，从而证明结论；（2）首先根据勾股定理求出BC 的长度，然后证明BCD BAC ∽△△，最后利用CD BD AC BC=求解即可． 【详解】（1）证明：连接OD ，如图，∵BC 是O 的直径，∴90BDC ∠=︒，∴90ADC ∠=︒，∵E 为AC 的中点， ∴12DE EC AC ==， ∴EDC ECD ∠=∠，∵OD OC = ，∴ODC OCD ∠=∠，∵AC 切O 于点C ，∴AC OC ⊥．∴90EDC ODC ECD OCD ∠+∠=∠+∠=︒，∴DE OD ⊥，∴DE 是O 的切线；（2）解：在Rt BCD 中，∵4BD =，3CD =，∴5BC ==∵90BDC BCA ∠=∠=︒，B B ∠=∠．∴BCD BAC ∽△△， ∴CD BD AC BC=， 即345AC =， ∴154=AC ．【点睛】本题主要考查圆的综合问题，掌握切线的判定及性质，相似三角形的判定及性质是解题的关键．13. 如图，在ABC ∆中，2AC =，4BC =，D 为BC 边上的一点，且CAD B ∠=∠．若ADC ∆的面积为a ，则ABD ∆的面积为（ ）A. 2aB. 52aC. 3aD. 72a 【答案】C【解析】 【分析】根据相似三角形的判定定理得到ACDBCA ∆∆，再由相似三角形的性质得到答案.【详解】∵CAD B ∠=∠，ACD BCA ∠=∠，∴ACD BCA ∆∆， ∴2ACD BCA S AC S AB ∆∆⎛⎫= ⎪⎝⎭，即14BCAa S ∆=，解得，BCA ∆的面积为4a ，∴ABD ∆的面积为：43a a a -=，故选C ．【点睛】本题考查相似三角形的判定定理和性质，解题的关键是熟练掌握相似三角形的判定定理和性质.14. 如图，点D 是△ABC 的边BC 的中点，且∠CAD ＝∠B ，若△ABC 的周长为10，则△ACD 的周长是（ ）A. 5 C. 52 D. 【答案】B【解析】 【分析】先根据已知证明△ACD ∽△BCA ，再根据相似三角形的性质得到AC 2=CD•CB ，设BD=CD=x ，得到x ，根据相似三角形的性质计算即可．【详解】解：∵∠CAD=∠B ，∠C=∠C ，∴△ACD ∽△BCA ， ∴AC CD BC AC=，即AC 2=CD•CB ， 设BD=CD=x ，∵点D 是△ABC 的边BC 的中点，∴BC=2x∴x ，∴=ABC 22ACD AC BC ==的周长的周长，即102ACD =的周长;∴△ACD 的周长故选B ．【点睛】本题考查的是相似三角形的判定和性质，掌握相似三角形的周长比等于相似比是解题的关键．。

三角形相似基本模型一、引言三角形是几何学中最基本的图形之一，而相似三角形则是三角形中的重要概念之一。

相似三角形是指具有相同形状但大小不同的两个三角形。

在实际生活中，我们经常会遇到需要利用相似三角形来解决问题的情况。

本文将介绍三种常见的三角形相似基本模型，并通过具体例子来说明其应用。

二、模型一：角-角相似在角-角相似模型中，两个三角形的对应角度相等。

具体来说，如果两个三角形的角度分别为A、B、C和A'、B'、C'，且满足A=A'、B=B'、C=C'，那么这两个三角形是相似的。

例如，已知三角形ABC与三角形A'B'C'的角度分别为∠A=40°、∠B=60°、∠C=80°，且∠A'=40°、∠B'=60°、∠C'=80°，则可以得出三角形ABC与三角形A'B'C'是相似的。

在实际应用中，我们可以利用角-角相似模型解决一些测量问题。

例如，在无法直接测量某个角度时，我们可以利用已知的相似三角形来计算出该角度的近似值。

三、模型二：边-边-边相似在边-边-边相似模型中，两个三角形的对应边长成比例。

具体来说，如果两个三角形的边长分别为a、b、c和a'、b'、c'，且满足a/a'=b/b'=c/c'，那么这两个三角形是相似的。

例如，已知三角形ABC的边长分别为AB=4cm、BC=6cm、AC=8cm，而三角形A'B'C'的边长分别为A'B'=8cm、B'C'=12cm、A'C'=16cm，则可以得出三角形ABC与三角形A'B'C'是相似的。

在实际应用中，我们经常会遇到需要测量无法直接测量的边长的情况。

相似三角形及其应用相似三角形是指两个或多个三角形的对应角度相等，并且对应的边长成比例。

在几何学中，相似三角形是一个重要的概念，具有广泛的应用。

本文将介绍相似三角形的性质以及它在实际问题中的应用。

一、相似三角形的性质1. AA相似定理：如果两个三角形的两个角分别相等，则这两个三角形相似。

2. SSS相似定理：如果两个三角形的三条边对应成比例，则这两个三角形相似。

3. SAS相似定理：如果两个三角形的两边成比例，且包含这两边的夹角相等，则这两个三角形相似。

4. 相似三角形中对应边的比例关系：如果三角形ABC与三角形DEF相似，那么AB与DE的比例等于AC与DF的比例，BC与EF的比例等于AC与DF的比例，AB与DE的比例等于BC与EF的比例。

二、相似三角形的应用1. 测量难以直接获取的距离：通过相似三角形的比例关系，可以利用已知的距离和长度来计算无法直接测量的距离和长度。

例如，在实际测绘中，可以通过测量一棵树的阴影以及测量人的身高和阴影长度，来计算树的高度。

2. 解决高空物体的测量问题：在很多时候，无法直接测量高空物体的高度，但可以通过相似三角形的比例关系来间接计算。

比如，在测量高楼的高度时，可以通过测量建筑物的阴影长度以及测量阴影与高楼的投影角度，来计算出高楼的实际高度。

3. 三角测量法的应用：在导航、航海和地理测量等领域，三角测量法是一种常用的测量技术。

这种方法利用相似三角形的性质，通过测量三角形的边长和角度来计算未知的长度和距离。

4. 建筑工程中的应用：在建筑工程中，相似三角形的概念经常被应用于设计、施工和测量。

通过相似三角形的比例关系，可以确定建筑物的尺寸、高度和角度，保证工程的准确性和稳定性。

5. 几何模型的相似：在计算机图形学和动画制作中，相似三角形的概念被广泛应用。

通过构建相似的几何模型，可以实现图形的放大、缩小和形变，从而实现各种特效和动画效果。

总结：相似三角形是几何学中一个重要的概念，用于描述两个或多个三角形的形状和尺寸关系。

相似三角形重要模型-手拉手模型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型，在实际的应用和解题当中出现时，对于同学们来说，都比较困难。

而深入理解模型内涵，灵活运用相关结论可以显著提高解题效率，本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。

手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等；②分子和分子组成一个三角形、分母和分母组成一个三角形；③第②步成立，直接从证这两个三角形相似，逆向证明到线段乘积相等；④第②步不成立，则选择替换掉线段比例式中的个别线段，之后再重复第③步。

模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义：如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变)，我们称这样的图形变换为旋转相似变换，这个顶点称为旋转相似中心，所得的三角形称为原三角形的旋转相似三角形。

1)手拉手相似模型(任意三角形)条件:如图，∠BAC =∠DAE =α，AD AB =AE AC=k ；结论：△ADE ∽△ABC ，△ABD ∽△ACE ；EC BD =k .2)手拉手相似模型(直角三角形)条件:如图，∠AOB =∠COD =90°，OC OA =OD OB =k (即△COD ∽△AOB )；结论：△AOC ∽△BOD ；BD AC =k ，AC ⊥BD ，S ABCD =12AB ×CD .3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点；结论：△BME ∽△CMF ；BE CF =3.条件:△ABC 和ADE 是等腰直角三角形；结论：△ABD ∽△ACE .1(2023秋·福建泉州·九年级校考期末)问题背景：(1)如图①，已知△ABC ∽△ADE ，求证：△ABD ∽△ACE ；尝试应用：(2)如图②，在△ABC 和△ADE 中，∠BAC =∠DAE =90°，∠ABC =∠ADE =60°，AC 与DE相交于点F ，点D 在BC 边上，DF CF=233，求AD BD 的值；拓展创新：(3)如图③，D 是△ABC 内一点，∠BAD =∠CBD =30°，∠BDC =90°，AB =4，AC =23，求AD 的长．【答案】(1)见解析；(2)AD BD =2；(3)AD =5【分析】问题背景(1)由题意得出AB AD =AC AE ，∠BAC =∠DAE ，则∠BAD =∠CAE ，可证得结论；尝试应用(2)连接EC ，证明△ABC ∽△ADE ，由(1)知△ABD ∽△ACE ，由相似三角形的性质得出AE AD =EC BD =3，∠ACE =∠ABD =∠ADE ，可证明△ADF ∽△ECF ，得出DF CF =AD CE=233，则可求出答案．拓展创新(3)过点A 作AB 的垂线，过点D 作AD 的垂线，两垂线交于点M ，连接BM ，证明△BDC ∽△MDA ，由相似三角形的性质得出BD MD =DC DA ，证明△BDM ∽△CDA ，得出BM CA =DM AD=3，求出BM =6，由勾股定理求出AM ，最后由直角三角形的性质可求出AD 的长．【详解】问题背景(1)证明：∵△ABC ∽△ADE ，∴AB AD =AC AE ，∠BAC =∠DAE ，∴∠BAD =∠CAE ，AB AC =AD AE，∴△ABD ∽△ACE ；尝试应用(2)解：如图，连接EC ，∵∠BAC=∠DAE=90°，∠ABC=∠ADE=60°，∴△ABC∽△ADE，AE=3AD由(1)知△ABD∽△ACE，∴AEAD=ECBD=3，∠ACE=∠ABD=∠ADE=60°，∴AEEC=ADBD，∵∠AFD=∠AEFC∴△ADF∽△ECF∴DFCF =ADCE∵DF CF =233∴DFCF=ADCE=233∴AD=233CE∴AE=3AD=2CE∴ADBD=AEEC=2，拓展创新(3)解：如图2，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，∵∠BAD=30°，∴∠DAM=60°，∴∠AMD=30°，∴∠AMD=∠DBC，又∵∠ADM=∠BDC=90°，∴△BDC∽△MDA，∴BDMD=DCDA，又∠BDC=∠ADM，∴∠BDC+∠CDM=∠ADM+∠CDM，即∠BDM=∠CDA，∴△BDM∽△CDA，∴BMCA=DMAD=3，∵AC=23，∴BM=23×3=6，∴AM=BM2-AB2=62-42=25，∴AD=12AM=5．【点睛】此题是相似形综合题，考查了直角三角形的性质，勾股定理，相似三角形的判定与性质等知识，熟练掌握相似三角形的判定与性质是解题的关键．2(2023秋·江苏无锡·九年级校考阶段练习)【模型呈现：材料阅读】如图，点B，C，E在同一直线上，点A，D在直线CE的同侧，△ABC和△CDE均为等边三角形，AE，BD 交于点F，对于上述问题，存在结论(不用证明)：(1)△BCD≌△ACE(2)△ACE可以看作是由△BCD绕点C旋转而成；⋯【模型改编：问题解决】点A ，D 在直线CE 的同侧，AB =AC ，ED =EC ，∠BAC =∠DEC =50°，直线AE ，BD 交于F ，如图1：点B 在直线CE 上，①求证：△BCD ∽△ACE ； ②求∠AFB 的度数． 如图2：将△ABC 绕点C 顺时针旋转一定角度．③补全图形，则∠AFB 的度数为；④若将“∠BAC =∠DEC =50°”改为“∠BAC =∠DEC =m °”，则∠AFB 的度数为．(直接写结论)【模型拓广：问题延伸】如图3：在矩形ABCD 和矩形DEFG 中，AB =2，AD =ED =23，DG =6，连接AG ，BF ，求BF AG 的值．图1 图2 图3【答案】【模型改编：问题解决】①见解析；②65°；③图见解析，115°；④90°+m °2【模型拓广：问题延伸】233【分析】【模型改编：问题解决】①先证明△ABC ∽△EDC ，可得AC EC =BC DC，再证明∠ACE =∠BCD ，可得△BCD ∽△ACE ；②由△BCD ∽△ACE ，可得∠DBC =∠EAC ，再结合三角形的外角可得答案；③连接EA 并延长交BD 于F ，同理可得：△BCD ∽△ACE ，∠CEF =∠BDC ，再结合三角形的外角可得答案；④先求解∠CDE =∠DCE =12180°-m ° =90°-12m °，结合③的思路可得答案；【模型拓广：问题延伸】连接BD 、DF ，先证明△ADB ∽△GDF ，可得∠ADB =∠GDF ，AD DG =BD DF ，证明∠ADG =∠BDF ，可得△BDF ∽△ADG ，可得BF AG =BD AD，从而可得答案．【详解】【模型改编：问题解决】①∵AB =AC ，ED =EC ，∠BAC =∠DEC =50°，∴∠ABC =∠ACB =180°-50° ÷2=65°，∠EDC =∠ECD =180°-50° ÷2=65°，∴△ABC ∽△EDC ，∴AC EC =BC DC，∵∠ACE =180°-∠ACB =115°，∠BCD =180°-∠DCE =115°，∴∠ACE =∠BCD ，∴△BCD ∽△ACE ；②由①知，△BCD ∽△ACE ，∴∠DBC =∠EAC ，∴∠AFB =∠DBC +∠CEA =∠EAC +∠CEA =∠ACB =65°③补图如下：连接EA 并延长交BD 于F ，图2同理可得：△BCD ∽△ACE ∴∠CEF =∠BDC ，∴∠AFB =∠BDC +∠CDE +∠DEF =∠CEF +∠CDE +∠DEF =∠CED +∠CDE =50°+65°=115°，④∵∠BAC =∠DEC =m °，CE =DE ，∴∠CDE =∠DCE =12180°-m ° =90°-12m °，同理③可得∠AFB =∠CED +∠CDE =m °+90°-12m °=90°+m °2，故答案为：90°+m °2；【模型拓广：问题延伸】连接BD 、DF ，图3∵在矩形ABCD 和矩形DEFG 中，AB =2，AD =ED =FG =23，DG =6，∴AB AD =GF DG =33，又∵∠BAD =∠DGF =90°，∴△ADB ∽△GDF ，∴∠ADB =∠GDF ，AD DG=BD DF ，∵∠ADG =∠GDF +∠ADF ，∠BDF =∠ADB +∠ADF ，∴∠ADG =∠BDF ，∴△BDF ∽△ADG ，∴BF AG =BD AD，∵AD =23，AB =2，∴BD =AB 2+AD 2=4，∴BF AG =BD AD =423=233．【点睛】本题考查的是等腰三角形的性质，矩形的性质，勾股定理的应用，相似三角形的判定与性质，熟练的证明三角形相似是解本题的关键．3(2023春·湖北黄冈·九年级专题练习)【问题呈现】△CAB 和△CDE 都是直角三角形，∠ACB =∠DCE =90°,CB =mCA ,CE =mCD ，连接AD ，BE ，探究AD ，BE 的位置关系．(1)如图1，当m =1时，直接写出AD ，BE 的位置关系：；(2)如图2，当m ≠1时，(1)中的结论是否成立？若成立，给出证明；若不成立，说明理由．【拓展应用】(3)当m =3,AB =47,DE =4时，将△CDE 绕点C 旋转，使A ,D ,E 三点恰好在同一直线上，求BE 的长．【答案】(1)BE ⊥AD (2)成立；理由见解析(3)BE =63或43【分析】(1)根据m =1，得出AC =BC ，DC =EC ，证明△DCA ≌△ECB ，得出∠DAC =∠CBE ，根据∠GAB +∠ABG =∠DAC +∠CAB +∠ABG ，求出∠GAB +∠ABG =90°，即可证明结论；(2)证明△DCA ∽△ECB ，得出∠DAC =∠CBE ，根据∠GAB +∠ABG =∠DAC +∠CAB +∠ABG ，求出∠GAB +∠ABG =90°，即可证明结论；(3)分两种情况，当点E 在线段AD 上时，当点D 在线段AE 上时，分别画出图形，根据勾股定理求出结果即可．【详解】(1)解：∵m =1，∴AC =BC ，DC =EC ，∵∠DCE =∠ACB =90°，∴∠DCA +∠ACE =∠ACE +∠ECB =90°，∴∠DCA =∠ECB ，∴△DCA ≌△ECB ，∴∠DAC =∠CBE ，∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG，=∠CBE+∠CAB+∠ABG=∠CAB+∠CBA=180°-∠ACB=90°，∴∠AGB=180°-90°=90°，∴BE⊥AD；故答案为：BE⊥AD．(2)解：成立；理由如下：∵∠DCE=∠ACB=90°，∴∠DCA+∠ACE=∠ACE+∠ECB=90°，∴∠DCA=∠ECB，∵DC CE =ACBC=1m，∴△DCA∽△ECB，∴∠DAC=∠CBE，∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG，=∠CBE+∠CAB+∠ABG =∠CAB+∠CBA=180°-∠ACB=90°，∴∠AGB=180°-90°=90°，∴BE⊥AD；(3)解：当点E在线段AD上时，连接BE，如图所示：设AE=x，则AD=AE+DE=x+4，根据解析(2)可知，△DCA∽△ECB，∴BE AD =BCAC=m=3，∴BE=3AD=3x+4=3x+43，根据解析(2)可知，BE⊥AD，∴∠AEB=90°，根据勾股定理得：AE2+BE2=AB2，即x2+3x+432=472，解得：x=2或x=-8(舍去)，∴此时BE=3x+43=63；当点D在线段AE上时，连接BE，如图所示：设AD=y，则AE=AD+DE=y+4，根据解析(2)可知，△DCA∽△ECB，∴BE AD =BCAC=m=3，∴BE=3AD=3y，根据解析(2)可知，BE⊥AD，∴∠AEB=90°，根据勾股定理得：AE 2+BE 2=AB 2，即y +4 2+3y 2=47 2，解得：y =4或y =-6(舍去)，∴此时BE =3y =43；综上分析可知，BE =63或43．【点睛】本题主要考查了全等三角形的判定和性质，相似三角形的判定和性质，三角形内角和定理的应用，勾股定理，解题的关键是熟练掌握三角形相似的判定方法，画出相应的图形，注意分类讨论．4(2023秋·福建泉州·九年级校考阶段练习)如图，已知△ABC 中，AB =AC ，∠BAC =α．点D 是△ABC 所在平面内不与点A 、C 重合的任意一点，连接CD ，将线段CD 绕点D 顺时针旋转α得到线段DE ，连接AD 、BE ．(1)如图1，当α=60°时，求证：BE =AD ．(2)当α=120°时，请判断线段BE 与AD 之间的数量关系是，并仅就图2的情形说明理由．(3)当α=90°时，且BE ⊥AB 时，若AB =8，BE =2，点E 在BC 上方，求CD 的长．【答案】(1)见解析，(2)BE =3AD ，理由见解析(3)82【分析】(1)先证明△ABC 和△DCE 是等边三角形，再证明△ADC ≌△BEC ，可推出BE =AD ；(2)过A 作AH ⊥BC 与H ，先根据含30°的直角三角形的性质，等腰三角形的性质以及勾股定理可求出BC =3AC ，同理求出CE =3CD ，可得出BC EC =3AC 3DC=AC DC ，证明∠DCA =∠BCE ，然后证明△EBC ∽△DAC 即可求解；(3)过E 作EF ⊥BC 于F ，可判断△BEF 是等腰直角三角形，然后可求出EF ，BF ，CF 的长度，由(2)同理可证出△EBC ∽△DAC ，最后根据相似三角形的性质即可求解．【详解】(1)解：∵旋转，∴CD =ED ，当α=60°时，又AB =AC ，∴△ABC 和△DCE 是等边三角形，∴AC =BC ，DC =EC ，∠DCE =∠ACB =60°，∴∠ACD =∠BCE ，∴△ADC ≌△BEC ，∴AD =BE ；(2)解：BE =3AD 过A 作AH ⊥BC 与H ，∵AB =AC ，∠BAC =α=120°，∴∠ACB =30°，CH =12BC ，∴AC =2AH ，又由勾股定理得AH 2+CH 2=AC 2，∴CH =32AC ，∴BC =3AC ，同理CE =3CD ，∵DC =EC ，∠CDE =α=120°，∴∠DCE =30°=∠ACB ，∴∠DCA =∠BCE ，∵BC =3AC ，CE =3CD ，∴BC EC =3AC 3DC =AC DC ，∴△EBC ∽△DAC ，∴BE AD =BC AC =3，即BE =3AD (3)解：如图，过E 作EF ⊥BC 于F ，当α=90°时，∵AC =AB =8，∴∠ACB =45°，BC =AB 2+AC 2=2AC =82，∵BE ⊥AB ，∴∠EBF =45°=∠BEF ，∴BF =EF ，∵BE =EF 2+BF 2=2EF =2，∴EF =BF =2，∴CF =BF +BC =92，∴CE =EF 2+CF 2=241，由(2)同理可证△EBC ∽△DAC ，∴EC DC =BC AC=2，即241DC =2，∴DC =82．【点睛】本题属于三角形综合题，考查了等边三角形的判定和性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理等知识，解题的关键在于正确寻找全等三角形或相似三角形．5(2023·黑龙江齐齐哈尔·统考中考真题)综合与实践数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．(1)发现问题：如图1，在△ABC 和△AEF 中，AB =AC ，AE =AF ，∠BAC =∠EAF =30°，连接BE ，CF，延长BE交CF于点D．则BE与CF的数量关系：，∠BDC=°；(2)类比探究：如图2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；(3)拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC=∠EAF=90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：；(4)实践应用：正方形ABCD中，AB=2，若平面内存在点P满足∠BPD=90°，PD=1，则S△ABP=．【答案】(1)BE=CF，30(2)BE=CF，∠BDC=60°，证明见解析(3)BF=CF+2AM(4)7+74或7-74【分析】(1)根据已知得出∠BAE=∠CAF，即可证明△BAE≌△CAF，得出BE=CF，∠ABE=∠ACF，进而根据三角形的外角的性质即可求解；(2)同(1)的方法即可得证；(3)同(1)的方法证明△BAE≌△CAF SAS，根据等腰直角三角形的性质得出AM=12EF=EM=MF，即可得出结论；(4)根据题意画出图形，连接BD，以BD为直径,BD的中点为圆心作圆，以D点为圆心，1为半径作圆，两圆交于点P,P1，延长BP至M，使得PM=DP=1，证明△ADP∽△BDM，得出PA=22BM，勾股定理求得PB，进而求得BM，根据相似三角形的性质即可得出PA=221+7=2+142，勾股定理求得BQ,PQ，进而根据三角形的面积公式即可求解．【详解】(1)解：∵∠BAC=∠EAF=30°，∴∠BAE=∠CAF，又∵AB=AC，AE=AF，∴△BAE≌△CAF，∴BE=CF，∠ABE=∠ACF设AC,BD交于点O，∵∠AOD=∠ACF+∠BDC=∠ABE+∠BAO∴∠BDC=∠BAO=∠BAC=30°，故答案为：BE= CF，30．(2)结论：BE=CF，∠BDC=60°；证明：∵∠BAC=∠EAF=120°，∴∠BAC-∠EAC=∠EAF-∠EAC，即∠BAE=∠CAF，又∵AB=AC，AE=AF，∴△BAE≌△CAF∴BE=CF，∠AEB=∠AFC∵∠EAF=120°，AE=AF，∴∠AEF=∠AFE=30°，∴∠BDC=∠BEF-∠EFD=∠AEB+30°-∠AFC-30°=60°，(3)BF=CF+2AM，理由如下，∵∠BAC=∠EAF=90°，∴∠BAC-∠EAC=∠EAF-∠EAC，即∠BAE=∠CAF，又∵△ABC和△AEF均为等腰直角三角形∴AB=AC,AE=AF，∴△BAE≌△CAF SAS，∴BE= CF，在Rt △AEF 中，AM ⊥BF ，∴AM =12EF =EM =MF ，∴BF =BE +EF =CF +2AM ；(4)解：如图所示，连接BD ，以BD 为直径,BD 的中点为圆心作圆，以D 点为圆心，1为半径作圆，两圆交于点P ,P 1，延长BP 至M ，使得PM =DP =1，则△MDP 是等腰直角三角形，∠MDP =45°∵∠CDB =45°,∴∠MDB =∠MDP +∠PDC +∠CDB =90°+∠PDC =∠ADP ，∵AD DB =12,DP DM =12，∴△ADP ∽△BDM ∴PA BM =12=22，∴PA =22BM ，∵AB =2，在Rt △DPB 中，PB =DB 2-DP 2=22 2-12=7，∴BM =BP +PM =7+1∴PA =221+7 =2+142过点P 作PQ ⊥AB 于点Q ，设QB =x ，则AQ =2-x ，在Rt △APQ 中，PQ 2=AP 2-AQ 2，在Rt △PBQ 中，PQ 2=PB 2-BQ 2∴AP 2-AQ 2=PB 2-BQ 2∴2+142 2-2-x 2=7 2-x 2解得：x =7-74，则BQ =7-74，设PQ ,BD 交于点G ，则△BQG 是等腰直角三角形，∴QG =QB =7-74在Rt △DPB ,Rt △DP 1B 中，DP =DP 1DB =DB ∴Rt △DPB ≌Rt △DP 1B ∴∠PDB =∠P 1DB又PD =P 1D =1，DG =DG ∴△PGD ≌△P 1DG ∴∠PGD =∠P 1GD =45°∴∠PGP 1=90°，∴P 1G ∥AB ∴S △ABP 1=12AB ×QG =12×2×7-74=7-74，在Rt △PQB 中，PQ =PB 2-BQ 2=7 2-7-74 2=7+74∴S△ABP =12AB ×PQ =12×2×7+74=7+74，综上所述，S△ABP=7+74或7-74故答案为：7+74或7-74．【点睛】本题考查了全等三角形的性质与判定，相似三角形的性质与判定，正方形的性质，勾股定理，直径所对的圆周角是直角，熟练运用已知模型是解题的关键．6(2023·山东济南·九年级统考期中)问题背景：一次小组合作探究课上，小明将一个正方形ABCD和等腰Rt△CEF按如图1所示的位置摆放(点B、C、E在同一条直线上)，其中∠ECF=90°．小组同学进行了如下探究，请你帮助解答：初步探究(1)如图2，将等腰Rt△CEF绕点C按顺时针方向旋转，连接BF，DE．请直接写出BF与DE的关系；(2)如图3，将(1)中的正方形ABCD和等腰Rt△CEF分别改成菱形ABCD和等腰△CEF，其中CE=CF，∠BCD=∠FCE，其他条件不变，求证：BF=DE；深入探究：(3)如图4，将(1)中的正方形ABCD和等腰Rt△CEF分别改成矩形ABCD和Rt△CEF，其中∠ECF=90°且CECF =CDBC=34，其它条件不变．①探索线段BF与DE的关系，说明理由；②连接DF，BE若CE=6，AB=12，直接写出DF2+BE2=．【答案】(1)BF=DE，BF⊥DE；(2)见解析；(3)①DEBF=34，DE⊥BF，见解析；②500【分析】(1)由正方形的性质，等腰直角三角形的性质，得到BC=CD，CE=CF，证明△BCF≌DCE，得到BF=DE，∠CBF=∠CDE，结合对顶角相等，即可得到BF⊥DE；(2)由菱形的性质，旋转的性质，先证明ΔBCF≌ΔDCE，即可得到结论成立；(3)①由矩形的性质，直角三角形的性质，先证明ΔBCF∽ΔDCE，得到BF与DE的数量关系，再由余角的性质证明位置关系即可；②连接BD，先求出矩形的边长，直角三角形的边长，与(1)同理先证明BF⊥DE，然后利用勾股定理，等量代换，即可得到DF2+BE2=500．【详解】解：(1)如图：∵正方形ABCD和等腰Rt△CEF中，∴BC=CD，CE=CF，∠BCD=∠ECF=90°，∴∠BCD+∠DCF=∠ECF+∠DCF，即∠BCF=∠DCE，∴△BCF≌DCE，∴BF=DE，∠CBF=∠CDE，∵∠BGC=∠DGF，∴∠BCG=∠DFG=90°∴BF⊥DE．(2)证明：如图：∵∠BCD=∠FCE，∴∠BCF=∠DCE，∵四边形ABCD为菱形∴BC=CD，又∵CE=CF∴△BCF≌△DCE(SAS)，∴BF=DE；(3)①∵在矩形ABCD中，∠BCD=90°，∴∠BCD=∠FCE∴∠BCF=∠DCE，又∵CECF=CDBC=34∴△BCF∽△DCE，∴DEBF=CECF=34；∴∠CBF=∠CDE，设CD与BF交于点G∵∠BGC=∠DGF∴180°-∠CBF-∠BGC=180°-∠CDE-∠DGF，∴∠DQB=∠BCD=90°∴DE⊥BF．②如图：连接BD在矩形ABCD中，CD=AB=12，∵CE=6，6CF =12BC=34，∴CF=8，BC=16，∵△BCF∽△DCE，∴∠CBF=∠CDE，∵∠BGC=∠DGF，∴∠BCG=∠DQG=90°，∴BF⊥DE；在直角△BCD中，有BD2=BC2+CD2=162+122=400，在直角△BDQ中，BD2=BQ2+DQ2=400；在直角△CEF中，EF2=CE2+CF2=62+82=100，在直角△EFQ中，EF2=EQ2+FQ2=100；∴BQ2+DQ2+EQ2+FQ2=400+100=500；在直角△BEQ和直角△DFQ中，由勾股定理，则∵BQ2+EQ2=BE2，DQ2+FQ2=DF2，∴DF2+BE2=BQ2+DQ2+EQ2+FQ2=500；故答案为：500．【点睛】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，旋转的性质，勾股定理，以及等腰直角三角形的性质等知识，解题的关键是熟练掌握所学的知识，正确的作出辅助线，找到证明三角形相似和三角形全等的条件进行解题．7(2023春·广东·九年级专题练习)已知在△ABC中，O为BC边的中点，连接AO，将△AOC绕点O顺时针方向旋转(旋转角为钝角)，得到△EOF，连接AE，CF．(1)如图1，当∠BAC=90°且AB=AC时，则AE与CF满足的数量关系是；(2)如图2，当∠BAC =90°且AB≠AC时，(1)中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；(3)如图3，延长AO到点D，使OD=OA，连接DE，当AO=CF=5，BC=6时，求DE的长．【答案】(1)AE=CF；(2)成立，证明见解析；(3)511 3【分析】(1)结论AE=CF．证明ΔAOE≅ΔCOF(SAS)，可得结论．(2)结论成立．证明方法类似(1)．(3)首先证明∠AED=90°，再利用相似三角形的性质求出AE，利用勾股定理求出DE即可．【详解】解：(1)结论：AE=CF．理由：如图1中，∵AB=AC，∠BAC=90°，OC=OB，∴OA=OC=OB，AO⊥BC，∵∠AOC=∠EOF=90°，∴∠AOE=∠COF，∵OA=OC，OE=OF，∴ΔAOE≅ΔCOF(SAS)，∴AE=CF．(2)结论成立．理由：如图2中，∵∠BAC=90°，OC=OB，∴OA=OC=OB，∵∠AOC=∠EOF，∴∠AOE=∠COF，∵OA=OC，OE=OF，∴ΔAOE≅ΔCOF(SAS)，∴AE=CF．(3)如图3中，由旋转的性质可知OE =OA ，∵OA =OD ，∴OE =OA =OD =5，∴∠AED =90°，∵OA =OE ，OC =OF ，∠AOE =∠COF ，∴OA OC =OE OF ，∴ΔAOE ∽ΔCOF ，∴AE CF =OA OC，∵CF =OA =5，∴AE 5=53，∴AE =253，∴DE =AD 2-AE 2=102-253 2=5113．【点睛】本题属于几何变换综合题，考查了旋转变换，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形或相似三角形解决问题，属于中考压轴题．课后专项训练1(2023秋·北京顺义·九年级校考期中)如图，△ABC 和△ADE 都是等腰直角三角形，∠ABC =∠ADE =90°．连接BD ，CE ．则BD CE的值为()A.12B.22C.2D.2【答案】B 【分析】由等腰直角三角形的性质可推出∠DAE =∠BAC =45°，AE =2AD ，AC =2AB ，从而可得出∠EAC =∠DAB ，AE AD =AC AB=2，证明△DAB ∽△EAC 即可得出结论．【详解】解：∵△ABC 和△ADE 都是等腰直角三角形，∴∠DAE =∠BAC =45°，AE =2AD ，AC =2AB ，∴∠EAC =∠DAB ，AE AD =AC AB =2，∴△DAB ∽△EAC ，∴BD CE =AD AE=22．故选B ．【点睛】本题考查等腰直角三角形的性质，勾股定理，相似三角形的判定和性质．掌握三角形相似的判定条件是解题关键．2(2023春·浙江金华·九年级校考期中)如图，在Rt △ABC 中，∠ABC =90°，以AB ，AC 为边分别向外作正方形ABFG 和正方形ACDE ，CG 交AB 于点M ，BD 交AC 于点N ．若GM CM =12，则CG BD=() A.12 B.34 C.255 D.13013【答案】D【分析】设AG =a =AB ，BC =2a ，由“AAS ”可证△ABC ≌△CHD ，可得AB =CH =a ，DH =BC =2a ，利用勾股定理分别求出CG ，BD 的长，即可求解．【详解】解：如图，过点D 作DP ⊥BC ，交AC 的延长线于点P，交BC 的延长线于点H ，∵AG ∥BF ，∴△AGM ∽△BCM ，∴AG BC =GM CM=12，∴设AG =a =AB ，BC =2a ，∴CG =GF 2+FC 2=a 2+(3a )2=10a ，∵DH ⊥BC ，AB ⊥BC ，∴∠DHC =∠ABC =∠ACD =90°，AB ∥DH ，∴∠DCH +∠ACB =90°=∠ACB +∠BAC ，∴∠DCH =∠BAC ，在△ABC 和△CHD 中，∠ABC =∠DHC ∠BAC =∠DCH AC =CD，∴△ABC ≌△CHD (AAS )，∴AB =CH =a ，DH =BC =2a ，∴BD =BH 2+DH 2=(3a )2+(2a )2=13a ，∴CG BD =10a 13a =13013．故选：D ．【点睛】本题考查了相似三角形的判定和性质，正方形的性质，全等三角形的判定和性质，添加恰当辅助线构造相似三角形是解题的关键．3(2023春·浙江丽水·九年级专题练习)如图，在△ABC 中，过点C 作CD ⊥AB ，垂足为点D ，过点D 分别作DE ⊥AC ，DF ⊥BC ，垂足分别为E ，F ．连接EF 交线段CD 于点O ，若CO =22，CD =32，则EO ⋅FO 的值为( )．A.63B.4C.56D.6【答案】B【分析】由题意易得出∠DEC=∠DFC=90°，即说明点C，E，D，F四点共圆，得出∠DEO=∠FCO，从而易证△DOE∽△FOC，得出EOCO=DOFO．由题意可求出DO=CD-CO=2，即可求出EO⋅FO=CO⋅DO=4．【详解】解：∵DE⊥AC，DF⊥BC，∴∠DEC=∠DFC=90°，∴点C，E，D，F四点共圆，∴∠DEF=∠FCD，即∠DEO=∠FCO．又∵∠DOE=∠FOC，∴△DOE∽△FOC，∴EOCO=DOFO，∴EO⋅FO=CO⋅DO．∵CO=22，CD=32，∴DO=CD-CO=2，∴EO⋅FO=CO⋅DO=22×2=4．故选B．【点睛】本题考查相似三角形的判定和性质，四点共圆的知识，圆周角定理．确定点C，E，D，F四点共圆，从而可得出证明△DOE∽△FOC的条件是解题关键．4(2022·广西梧州·统考一模)如图，在△ABC中，∠C=45°，将△ABC绕着点B逆时针方向旋转，使点C的对应点C′落在CA的延长线上，得到△A′BC′，连接AA′，交BC′于点O．下列结论：①∠AC′A′= 90°；②AA′=BC′；③∠A′BC′=∠A′AC′；④△A′OC′∽△BOA．其中正确结论的个数是()A.1B.2C.3D.4【答案】C【分析】利用旋转的性质和等腰三角形的性质推出∠AC A =90°，即可判断①的正确性；通过点A 、B、A、C 四点共圆可以判断出②③④的正确性．【详解】解：由题意可得：BC=BC ，∠C=∠A C B∵∠C=45°∴∠BC A=45°∵∠AC A =∠A C B+∠BC A∴∠AC A =90°，故①正确；∵∠BC A=∠C=45°∴∠C BC=90°∵∠ABC=∠A BC ∴∠A BA=90°∴∠A BA+∠AC A =180°，∠C AB+∠C A B=180°∴点A 、B、A、C 四点共圆∵∠AC A =90°，∠BAC ≠90°∴A A是直径，BC 不是直径∴A A≠BC ，故②错误；∵点A 、B、A、C 四点共圆∴∠A BC =∠A AC ，故③正确；∵点A 、B、A、C 四点共圆∴∠AA C =∠ABC ，∠A C B=∠A AB∴△A OC ∽△BOA，故④正确；∴正确结论的个数是3个故选C．【点睛】本题考查了图形的旋转、等腰三角形的性质、四点共圆、圆周角定理的推论以及相似的判定等知识点，灵活运用这些知识点是解题的关键．5(2023·广东深圳·校联考模拟预测)如图，已知▱ABCD ，AB =3，AD =8，将▱ABCD 绕点A 顺时针旋转得到▱AEFG ，且点G 落在对角线AC 上，延长AB 交EF 于点H ，则FH 的长为．【答案】558【分析】先利用平行四边形的性质得到CD =AB =3，BC =AD =8，∠D =∠ABC ，再根据旋转的性质得到∠DAG =∠BAE ，AE =AB =3，EF =BC =8，∠E =∠ABC ，接着证明△ADC ∽△AEH ，然后利用相似比求出EH ，从而得到FH 的长．【详解】解：∵四边形ABCD 为平行四边形，∴CD =AB =3，BC =AD =8，∠D =∠ABC ，∵将▱ABCD 绕点A 顺时针旋转得到▱AEFG ，且点G 落在对角线AC 上，∴∠DAG =∠BAE ，AE =AB =3，EF =BC =8，∠E =∠ABC ，∴∠E =∠D ，∵∠DAC =∠HAE ，∴△ADC ∽△AEH ，∴AD AE =DC EH ，∴83=3EH ，∴EH =98，∴FH =EF -EH =8-98=558，故答案为：558．【点睛】本题考查了平行四边形的性质，旋转、三角形相似的判定利用三角形相似比求线段的长，根据旋转的性质得到∠DAG =∠BAE ，然后根据两组对应角分别相等的两三角形相似得出AD AE=DC EH 是本题的关键．6(2022·安徽·模拟预测)如图，将边长为3的菱形ABCD 绕点A 逆时针旋转到菱形AB C D 的位置，使点B 落在BC 上，B C 与CD 交于点E ．若BB =1，则CE 的长为．【答案】34/0.75【分析】延长D D 交BC 的延长线于点M ，过点C 作CN ∥DM 交B C 于点N ，根据菱形的性质和旋转的性质证明△ABB ≌△ADD ≌△DCM ≌B C M ，求得C D =B C =2，CM =C M =1，再根据CN ∥DM ，得CN MC =B C B M ，CN DC=CE DE ，代入即可求解．【详解】解：如图，延长D D 交BC 的延长线于点M ，过点C 作CN ∥DN 交B C 于点N ，∵四边形ABCD是菱形∴AB=BC=CD=AD=3，∠B=∠ADC=∠D ，AB∥CD∴∠DCM=∠B由旋转的性质得：AB =AB=3，AD =AD=3，∠BAB =∠DAD =∠MB C ，B C =D C =3，∠ADC=∠D ，∴△ABB ≌△ADD ∴DD =BB =1∴DC =D C -DD =2∵∠CDM+∠ADC=∠DAD +∠D ∴∠BAB =∠DAD =∠CDM∴△ABB ≌△DCM≌B C M，∴DM=AB =3，∠M=∠AB B∴C M=CM=3-2=1∵CN∥DM∴△B CN∽△B MC ∴CNMC =B CB M∵B C=BC-BB =2∴CN1=23∴CN=23∵CN∥DM∴△CNE∽△DC E∴CNDC =CEDE∴232=CE3-CE∴CE=34故答案为：34【点睛】本题考查菱形的性质，旋转的性质，全等三角形的判定与性质，相似三角形的判定与性质，综合性较强，作辅助线构造全等三角形和相似三角形是解题的关键．7(2021·湖南益阳·统考中考真题)如图，Rt△ABC中，∠BAC=90°,tan∠ABC=32，将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB C ，连接BB ，CC ，则△CAC 与△BAB 的面积之比等于．【答案】9:4【分析】先根据正切三角函数的定义可得ACAB=32，再根据旋转的性质可得AB=AB,AC=AC ,∠BAB=∠CAC =α，从而可得ACAC =ABAB=1，然后根据相似三角形的判定可得△CAC ∼△BAB ，最后根据相似三角形的性质即可得．【详解】解：∵在Rt△ABC中，∠BAC=90°,tan∠ABC=32，∴ACAB=32，由旋转的性质得：AB=AB ,AC=AC ,∠BAB =∠CAC =α，∴ACAC=ABAB=1，在△CAC 和△BAB 中，ACAC=ABAB∠CAC =∠BAB，∴△CAC ∼△BAB ，∴S△CACS△BAB=ACAB2=94，即△CAC 与△BAB 的面积之比等于9:4，故答案为：9:4．【点睛】本题考查了正切三角函数、旋转的性质、相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题关键．8(2023秋·山东济南·九年级校考阶段练习)如图，已知∠ACB=∠DCE=90°，∠ABC=∠CED=∠CAE=30°．(1)求证：△ACD∽△BCE；(2)若AC=3，AE=8，求AD．【答案】(1)见详解(2)AD=103 3【分析】(1)根据30°的正切值得ACBC=DCEC，即可证明相似．(2)先证明∠BAE=90°，进而求出BE=10，再根据△ACD∽△BCE得出ADBE=ACBC=DCEC=33，即可求出AD=33BE=1033．【详解】(1)∵∠ACB=∠DCE=90°∴∠ACD=∠BCE∵∠ABC=∠CED=∠CAE=30°∴tan∠ABC=ACBC =33，tan∠CED=DCEC=33∴AC BC =DCEC∴△ACD∽△BCE(2)∵由(1)，△ACD∽△BCE∴ADBE =ACBC=DCEC=33∵∠ABC=∠CED=∠CAE=30°∴∠BAC=60°∴∠BAE=90°∵AC=3，∠ABC=30°∴AB=2AC=6∵AE=8∴BE=10∴AD=33BE=1033【点睛】本题考查相似三角形的判定、特殊角三角函数值及勾股定理，根据特殊角得出对应线段成比例是解题关键．9(2023·安徽滁州·九年级校考阶段练习)如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，CD与BE、AE分别交于点P、M．求证：(1)△BAE∽△CAD；(2)MP⋅MD=MA⋅ME．【答案】(1)证明见解析(2)证明见解析【分析】(1)由题意可得AC=2AB，AD=2AE，∠BAE=∠CAD=135°，即可证△BAE∽△CAD；(2)由△BAE∽△CAD可得∠BEA=∠CDA，即可证△PME∽△AMD，可得MP⋅MD=MA⋅ME．【详解】(1)证明：∵等腰Rt △ABC 和等腰Rt △ADE ，∴AB =BC ，AE =DE ，∠BAC =∠DAE =45°，∴AC =2AB ，AD =2AE ，∠BAE =∠CAD =135°，∴AC AB =AD AE=2，∴△BAE ∽△CAD ，(2)∵△BAE ∽△CAD ，∴∠BEA =∠CDA ，且∠PME =∠AMD ，∴△PME ∽△AMD ，∴ME MD =MP AM，∴MP ⋅MD =MA ⋅ME ．【点睛】本题考查了相似三角形的判定和性质，等腰直角三角形性质，勾股定理的应用，熟练运用相似三角形的判定是本题的关键．10(2023秋·湖北孝感·九年级校联考阶段练习)问题背景：如图1，在△ABC 中，∠ACB =90°，AC =BC ，AD 是BC 边上的中线，E 是AD 上一点，将△CAE 绕点C 逆时针旋转90°得到△CBF ，AD 的延长线交BF 于点P ．问题探究：(1)当点P 在线段BF 上时，证明EP +FP =2BP ．①先将问题特殊化，如图2，当CE ⊥AD 时，证明：EP +FP =2BP ；②再探究一般情形，如图1，当CE 不垂直AD 时，证明：EP +FP =2BP ；拓展探究：(2)如图3，若AD 的延长线交BF 的延长线于点P 时，直接写出一个等式，表示EP ，FP ，BP 之间的数量关系．【答案】(1)①见解析，②见解析(2)EP -FP =2PB【分析】①结论：PE +PF =2PB ．根据旋转的性质△ACE ≌△BCF ，再证明四边形CEPF 是正方形，可得结论．②结论不变，如图2中，过点C 作CG ⊥AD 于点G ，过点C 作CH ⊥BF 交BF 的延长线于点H ．证明△CHF ≌△CGE ，可以推出FH =EG ，再利用正方形的性质解决问题即可．(2)结论：EP -FP =2PB ，证明方法类似②．【详解】(1)①证明：∵CE ⊥AD ，∴∠AEC =∠PEC =90°，在△ABC 中，∠ACB =90°，AC =AB ，∵将△CAE 绕点C 逆时针旋转90°得到△CBF ，∴△ACE ≌△BCF ，CF =CE ，∠ECF =90°，∠BFC =∠AEC =90°，∴∠BFC =∠ECF =∠PEC =90°，∴四边形CEPF 是矩形，∵CE =CF ，∴四边形CEPF 是正方形，∴CE =EP =FP =CF ，∠EPF =90°，∴∠BPD =90°=∠CED ，∵AD 是△ABC 中BC 边上的中线，∴BD =CD =12BC ，在△CED 和△BPD 中，∴∠CED =∠BPD∠CDE =∠BDP CD =BD，∴△CED ≌△BPD (AAS )，∴CE =BP ，∴BP =EP =CE =FP ，∴EP +FP =2BP②结论成立，证明：过点C 作CG ⊥AD 于点G ，过点C 作CH ⊥BF 交BF 的延长线于点H ．则∠CGE =∠CGD =∠CHF =90°．由旋转性质可知，△CBF≌△CAE，∴CF=CE，∠CFB=∠CEA，∠ACE=∠BCF，∵∠CFH=180°-∠CFB，∠CEG=180°-∠CEA，∴∠CFH=∠CEG，∴△CHF≌△CGE，∴∠FCH=∠ECG，CH=CG，FH=EG．∴∠FCH+∠BCF+∠DCG=∠ECG+∠ACF+∠DCG=90°．∴∠HCG=90°．∴四边形CGPH是正方形．∴CG=GP=PH，∴EP+FP=GP+PH=2CG．∵CD=BD，∠CGD=∠BPD=90°，∠CDG=∠BDP，∴△CDG≌△BDP．∴CG=BP．∴EP+FP=2PB．(2)解：EP-FP=2PB．理由：如下图所示，过C作CN∥BP交AP于点N，CM∥DP交BP的延长线于点M，则四边形CNPM是平行四边形，△BPD∽△BMC，∴CN=PM,CM=PN，BPBM =BDBC=12，∴BM=2BP，∴PM=BP，∵∠APB=90°，∴∠NPM=90°，∴四边形CNPM是矩形，∴∠M=∠CNE=∠CNP=90°，在△CFM和△CEN中，∠H=∠CNE=90°∠CFH=∠CEN CF=CE，∴△CFM≌△CEN(AAS)，∴CM=CN，FM=EN，∴四边形CNPM是正方形，∴PM=CN=PN，∴EP-FP=PN+EN-FP=PN+FM-FP=PN +PM=2PM，∴EP-FP=2BP．【点睛】本题属于几何变换综合题，考查相似三角形的判定和性质，等腰直角三角形的性质，全等三角形的判定和性质，正方形的判定和性质等知识，解题关键是正确寻找全等三角形解决问题，属于中考压轴题．11(2022·河南·九年级专题练习)规定：有一角重合，且角的两边叠合在一起的两个相似四边形叫做“嵌套四边形”，如图，四边形ABCD和AMPN就是嵌套四边形．(1)问题联想：如图①，嵌套四边形ABCD，AMPN都是正方形，现把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N'，连接BM'，DN'交于点O，则BM'与DN'的数量关系为，位置关系为；(2)类比探究：如图②，将(1)中的正方形换成菱形，∠BAD=∠MAN=60，其他条件不变，则(1)中的结论还成立吗?若成立，请说明理由；若不成立，请给出正确的结论，并说明理由；(3)拓展延伸：如图3，将(1)中的嵌套四边形ABCD和AMPN换成是长和宽之比为2:1的矩形，旋转角换成α(90°<α<180°)，其他条件不变，请直接写出BM'与DN'的数量关系和位置关系．【答案】(1)BM =DN ，BM ⊥DN ；(2)BM =DN 成立，BM ⊥DN 不成立，BM 与DN 相交，且夹角为60°.理由见解析；(3)BM =2DN ，BM ⊥DN .【分析】(1)根据SAS证明△ABM'≌△AND'，进而得到BM =DN ，∠ABM'=∠ADN'，再利用三角形内角和可推出∠BOD=90°，即BM ⊥DN ；(2)根据旋转和菱形的性质证明ΔABM ≌ΔADN ，再推出∠BOD=∠BAD=60°，故可求解；(3)根据旋转和矩形的性质证明ΔABM ∼ΔADN ，得到BM =2DN ，再推出∠BOD=∠BAD=90°即可求解．【详解】(1)如图设AB，DN 交于点H，，∵四边形ABCD，AMPN都是正方形，把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N'，∴AB=AD,AM'=AD', ∠BAM =∠DAN =150°∴△ABM'≌△AND'，∴BM =DN ，∠ABM'=∠ADN'，∵∠ADN'+∠DHA+∠DAH=180°，∠ABM'+∠BHO+∠BOD=180°，又∠DHA=∠BHO∴∠BOD=∠BAD=90°，即BM ⊥DN 故答案为：BM =DN ，BM ⊥DN ；(2)BM =DN 成立，BM ⊥DN 不成立，BM 与DN 相交，且夹角为60°.理由：设AB，DN 交于点E，由旋转的性质可得∠BAM =∠DAN =150°.∵四边形ABCD，AM P N 都是菱形，∴AB=AD，AM =AN ，∴ΔABM ≌ΔADN ，∴BM =DN ，∠ABM =∠ADN .。

相似三角形的九大模型1.在三角形ABC中，已知2.在三角形ABC中，CD为边AB上的高，正方形EFGH 的四个顶点分别在三角形ABC上，证明：111+EF^2=AB^2+BC^2+AC^2.3.在矩形ABCD中，AB=2，BC=3，点E、F、G、H分别在矩形ABCD的各边上，且EF∥HG∥AC，EH∥FG∥BD，则四边形EFGH的周长是10.4.在三角形ABC中，M是AC的中点，E是AB上一点，且BE=3AE，求BC的值。

5.在三角形ABC中，D、E分别为边AB、AC上的点，且∠ADE=∠ACB。

证明：AD×AB=AE×AC。

如果三角形ABC的面积为m，DE=3，BC=5，求三角形ADE的面积。

6.在三角形ABC中，点D、E分别在边AB、AC上，DE、BC的延长线相交于点F，且EF×DF=BF×CF。

证明：AD×AB=AE×AC。

当AB=12，AC=9，AE=8时，求BD的长与△ADE的面积。

7.将三角形纸片△ABC按如图所示的方式折叠，使点C落在AB边上的点D，折痕为EF。

已知AB=AC=3，BC=4，若以点B、D、F为顶点的三角形与△ABC相似，那么CF的长度是2/7.8.将三角形ABC纸片按如图所示的方式折叠，使点B落在边AC上，记为点B'，折痕为EF。

已知AB=AC=6，BC=8.求△ABC的周长。

若以点B'、F、C为顶点的三角形与△XXX 相似，求BF的长。

9.在三角形ABC中，AB=6，BC=8.点D以每秒1个单位长度的速度由B向A运动，同时点E以每秒2个单位长度的速度由C向B运动，当点E停止运动时，点D也随之停止。

设运动时间为t秒，当以B、D、E为顶点的三角形与△ABC相似时，求t的值。

10.在锐角三角形ABC中，AG⊥BC于点G，点D、E分别在XXX、AB上，XXX⊥DE于点F，且∠EAF=∠GAC。

证明：△ADE∽△ABC。

模型探究相似三角形考查范围广，综合性强，其模型种类多，其中有关一线三垂直模型在前面的专题已经很详细的讲解，这里就不在重复.模型一、A字型相似模型A字型（平行）反A字型（不平行）模型二、8字型与反8字型相似模型模型三、AX型相似模型（A字型及X字型两者相结合）模型四、共边角相似模型（子母型）模型五、手拉手相似模型考点一、A 字相似模型【例1】．如图，在△ABC 中，∠A ＝78°，AB ＝4，AC ＝6，将△ABC 沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（ ）A ．B ．C ．D ．➢变式训练 【变式1-1】．如图，在△ABC 中，DE ∥BC ，AH ⊥BC 于点H ，与DE 交于点G ．若，则＝ ．例题精讲【变式1-2】.如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM 并延长，交BC的延长线于D，则＝__________.【变式1-3】．如图，在△ABC中，点D在边AB上，AD＝9，BD＝7．AC＝12．△ABC的角平分线AE交CD于点F．（1）求证：△ACD∽△ABC；（2）若AF＝8，求AE的长度．考点二、8字与反8字相似模型【例2】．如图，AG∥BD，AF：FB＝1：2，BC：CD＝2：1，求的值➢变式训练【变式2-1】．如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（）A．B．C．D．【变式2-2】．如图，在平行四边形ABCD中，E为边AD的中点，连接AC，BE交于点F．若△AEF的面积为2，则△ABC的面积为（）A．8B．10C．12D．14【变式2-3】.如图，锐角三角形ABC中，∠A＝60°，BE⊥AC于E，CD⊥AB于D，则DE：BC＝．考点三、AX型相似模型（A字型及X字型两者相结合）【例3】.如图，在△ABC中，点D和E分别是边AB和AC的中点，连接DE，DC与BE交于点O，若△DOE的面积为1，则△ABC的面积为（）A．6B．9C．12D．13.5➢变式训练【变式3-1】.如图，DE是△ABC的中位线，F为DE中点，连接AF并延长交BC于点G，若S△EFG＝1，则S△ABC＝．【变式3-2】．如图：AD∥EG∥BC，EG交DB于点F，已知AD＝6，BC＝8，AE＝6，EF ＝2．（1）求EB的长；（2）求FG的长．【变式3-3】.如图，已知AB∥CD，AC与BD相交于点E，点F在线段BC上，，．（1）求证：AB∥EF；（2）求S△ABE：S△EBC：S△ECD．模型四、子母型相似模型【例4】.如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB＝120°，求证：（1）△ACP∽△PDB，（2）CD2＝AC•BD．➢变式训练【变式4-1】.如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A．∠ABP＝∠C B．∠APB＝∠ABC C．D．【变式4-2】.如图，在△ABC中，点D在AC边上，连接BD，若∠ABC+∠BDC＝180°，AD＝2，CD＝4，则AB的长为（）A．3B．4C．D．2【变式4-3】．如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则P A+PB 的最小值为．模型五、手拉手相似模型【例5】.如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD：BE的值为．➢变式训练【变式5-1】.如图，在△ABC与△ADE中，∠BAC＝∠DAE，∠ABC＝∠ADE．求证：（1）△BAC∽△DAE；（2）△BAD∽△CAE．【变式5-2】.如图，点D是△ABC内一点，且∠BDC＝90°，AB＝2，AC＝，∠BAD＝∠CBD＝30°，AD＝．【变式5-3】．如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB（k为常数），则BD的长为．（用含k的式子表示）实战演练1．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．＝B．C．D．2．如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为（）A．2：3B．2：5C．4：9D．：3．如图，菱形ABCD中，E点在BC上，F点在CD上，G点、H点在AD上，且AE∥HC ∥GF．若AH＝8，HG＝5，GD＝4，则下列选项中的线段，何者长度最长？（）A．CF B．FD C．BE D．EC4．如图，在△ABC中，BC＝6，E，F分别是AB，AC的中点，动点P在射线EF上，BP 交CE于点D，∠CBP的平分线交CE于点Q，当CQ＝CE时，EP+BP的值为（）A．6B．9C．12D．185．如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝2，AD＝2，将△ABC绕点C顺时针方向旋转后得△A′B′C，当A′B′恰好经过点D时，△B′CD为等腰三角形，若BB′＝2，则AA′等于（）A．B．2C．D．6．如图，已知，△ABC中边AB上一点P，且∠ACP＝∠B，AC＝4，AP＝2，则BP＝．7．如图，在▱ABCD中，AC、BD相交于点O，点E是OA的中点，联结BE并延长交AD 于点F，如果△AEF的面积是4，那么△BCE的面积是．8．如图，在△ABC中，点G为ABC的重心，过点G作DE∥AC分别交边AB、BC于点D、E，过点D作DF∥BC交AC于点F，如果DF＝4，那么BE的长为．9．如图，已知Rt△ABC中，两条直角边AB＝3，BC＝4，将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，并且点A落在DE边上，则sin∠ABE＝．10．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．（1）求线段DE的长；（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求的值．11．如图，在菱形ABCD中，∠ADE、∠CDF分别交BC、AB于点E、F，DF交对角线AC 于点M，且∠ADE＝∠CDF．（1）求证：CE＝AF；（2）连接ME，若＝，AF＝2，求ME的长．12．[问题背景]（1）如图①，已知△ABC∽△ADE，求证：△ABD∽△ACE．[尝试应用]（2）如图②，在△ABC和△ADE中，∠BAC＝∠DAE＝90°∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，①填空：＝；②求的值．13．如图，在正方形ABCD中，AB＝4，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于点M、N，连接EN、EF．（1）求证：△ABN∽△MBE；（2）求证：BM2+ND2＝MN2；（3）①求△CEF的周长；②若点G、F分别是EF、CD的中点，连接NG，则NG的长为．14．问题背景如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；尝试应用如图（2），在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，求的值；拓展创新如图（3），D是△ABC内一点，∠BAD＝∠CBD＝30°，∠BDC＝90°，AB ＝4，AC＝2，直接写出AD的长．15．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的数量关系BG＝DE及所在直线的位置关系BG⊥DE；②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断；（2）将原题中正方形改为矩形（如图4﹣6），且AB＝a，BC＝b，CE＝ka，CG＝kb（a ≠b，k＞0），则线段BG、线段DE的数量关系＝及所在直线的位置关系BG ⊥DE；（3）在第（2）题图5中，连接DG、BE，且a＝4，b＝3，k＝，直接写出BE2+DG2的值为．。

相似三角形常见模型[总结]相似三角形常见模型相似三角形是初中数学中一个重要的概念，也是解题过程中常见的模型。

通过研究和总结相似三角形的常见模型，可以帮助我们更好地理解和应用这个概念。

本文将从角度相似、边长比例和投影相似三个方面进行内容阐述。

一、角度相似在相似三角形中，角度是最直观的相似特征。

如果两个三角形的对应角相等，那么它们就是相似三角形。

根据这一特性，我们可以应用以下模型：1. AA相似模型当两个三角形中角的对应边分别相等时，这两个三角形相似。

这个模型常用于证明和构造相似三角形。

例如，在已知一个角相等的情况下，可以通过构造等腰三角形来证明相似。

2. AAA相似模型当两个三角形的三个角分别相等时，这两个三角形相似。

这个模型常用于解题中，当我们已知两个三角形的三个角分别相等时，可以得出它们是相似三角形的结论。

二、边长比例在相似三角形中，边长的比例关系也是常见的模型。

如果两个三角形的对应边的比值相等，那么它们是相似三角形。

根据这一特性，我们可以应用以下模型：1. 直角三角形边长模型在一个直角三角形中，由勾股定理可知，两直角边的平方和等于斜边的平方。

如果两个直角三角形斜边的比例相等，那么它们是相似的。

这个模型常用于解决与直角三角形相关的问题。

2. 形状类似三角形边长模型当两个三角形形状相似时，它们的对应边长之比也相等。

例如，当一个等边三角形与一个正三角形形状相似时，它们的对应边长比例为1:2。

这个模型常用于解决与形状类似三角形相关的问题。

三、投影相似在相似三角形中，投影的相似关系也是一种常见的模型。

当两个三角形的两直角边分别成比例时，它们是相似三角形。

根据这一特性，我们可以应用以下模型：1. 倒影相似模型当两个直角三角形的一条直角边与另一个直角三角形的斜边成比例时，它们是相似的。

这个模型常用于解决与倒影相似三角形相关的问题。

2. 旁影相似模型当两个直角三角形的一条直角边与另一个直角三角形的直角边成比例时，它们是相似的。

相似三角形模型分析大全1、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型）B（平行）B（不平行）（二）8字型、反8字型BCBC（蝴蝶型）（平行）（不平行）（三）母子型B（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（6）双垂型：2、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展B一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：．OE OA OC ⋅=2例2：已知：如图，△ABC 中，点E 在中线AD 上, ．ABC DEB ∠=∠求证：（1）； （2）．DA DE DB ⋅=2DAC DCE ∠=∠ACDEB例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：．EG EF BE ⋅=2相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：．FC FB FD ⋅=22、已知：AD 是Rt△ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME∽△NMD; (2)ND =NC·NB23、已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于D，E是AC上一点，CF⊥BE于F。

求证：EB·DF=AE·DB⊥，垂足为F，延长AD到G，使DG=EF，M是AH的中点。

4.在∆ABC中，AB=AC，高AD与BE交于H，EF BCGBM90求证：∠=︒5．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）已知：如图，在Rt△ABC 中，∠C =90°，BC =2，AC =4，P 是斜边AB 上的一个动点，PD ⊥AB ，交边AC于点D （点D 与点A 、C 都不重合），E 是射线DC 上一点，且∠EPD =∠A ．设A 、P 两点的距离为x ，△BEP 的面积为y ．（1）求证：AE =2PE ；（2）求y 关于x 的函数解析式，并写出它的定义域；（3）当△BEP 与△ABC 相似时，求△BEP 的面积．双垂型1、如图，在△ABC 中，∠A=60°，BD 、CE 分别是AC 、AB 上的高A（第25题图）求证：（1）△ABD∽△ACE；（2）△ADE∽△ABC；(3)BC=2ED2、如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=6，求：点B 到直线AC 的距离。

相似三角形的九大模型相似三角形是几何学中一类重要的图形，它具有一些独特的性质和模型。

这些模型可以用来解决各种实际问题，从简单的长度关系到复杂的空间结构。

本文将介绍相似三角形的九大模型，并给出相应的例子和应用场景。

相似三角形是指两个三角形形状相同，大小成比例。

相似三角形的对应边成比例，对应角相等。

相似三角形还有一些其他的性质，例如，相似三角形的中线、角平分线、高的比等于它们的相似比。

平行线模型：两个三角形分别在两条平行线上，它们的对应边平行且成比例。

这种模型经常用于解决一些与长度和角度相关的问题。

共顶点模型：两个三角形有一个共同的顶点，且它们的对应边成比例。

这种模型常用于证明两个三角形相似，以及求解一些角度问题。

角平分线模型：一个三角形的角平分线将这个三角形分成两个小的相似三角形。

这种模型可以用于证明两个三角形相似，以及求解一些角度问题。

平行四边形模型：一个平行四边形被它的两条对角线分成四个小的相似三角形。

这种模型可以用于解决一些与面积和长度相关的问题。

位似模型：一个相似变换将一个三角形映射到另一个三角形，这种变换称为位似变换。

这种模型可以用于解决一些与长度、角度和面积相关的问题。

旋转模型：一个三角形绕着它的一个顶点旋转一定的角度后得到另一个三角形，这两个三角形是相似的。

这种模型可以用于解决一些与角度和长度相关的问题。

镜像模型：一个三角形沿一条直线翻折后得到另一个三角形，这两个三角形是相似的。

这种模型可以用于解决一些与长度和角度相关的问题。

传递模型：如果一个三角形与另一个三角形相似，那么这个三角形的每一个部分都与另一个三角形的对应部分相似。

这种模型可以用于解决一些与长度和角度相关的问题。

扩展模型：如果一个三角形与另一个三角形相似，那么这个三角形的每一个部分都与另一个三角形的对应部分成比例。

这种模型可以用于解决一些与长度和角度相关的问题。

相似三角形的九创作者是几何学中一类重要的模型，它们具有广泛的应用价值。

第一部分 相似三角形模型分析大全一、相似三角形判定的基本模型认识（一）A 字型、反A 字型（斜A 字型）ABCDE（平行）CBA DE（不平行）（二）8字型、反8字型J OADBCAB CD（蝴蝶型）（平行） （不平行）（三）母子型ABCDCAD（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：CAD二、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ． 求证：OE OA OC ⋅=2．例2：已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2； （2）DAC DCE ∠=∠．例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ． 求证：EG EF BE ⋅=2．相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ⋅=2．AC D E B2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。

求证：EB ·DF=AE ·DB4.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。