SPSS相关性和回归分析一元线性方程案例解析
- 格式:doc
- 大小:455.50 KB
- 文档页数:8
用SPSS做一元线性回归分析粮食生产是一个关系到国家生存与发展的一个重要问题,粮食产量波动,制约着国民经济发展,影响着粮食的价格。
因此,研究影响粮食产量波动的因素的意义不可小觑。
本次分析主要通过SPSS以及线性回归分析方法,研究分析粮食产量与土地灌溉面积之间的关系。
大致的操作过程为:首先做散点图,查看两因素之间是否线性相关;如果线性相关,接着做线性回归分析,揭示其数量关系。
最后对回归方程做显著性检验以及经济意义的检验。
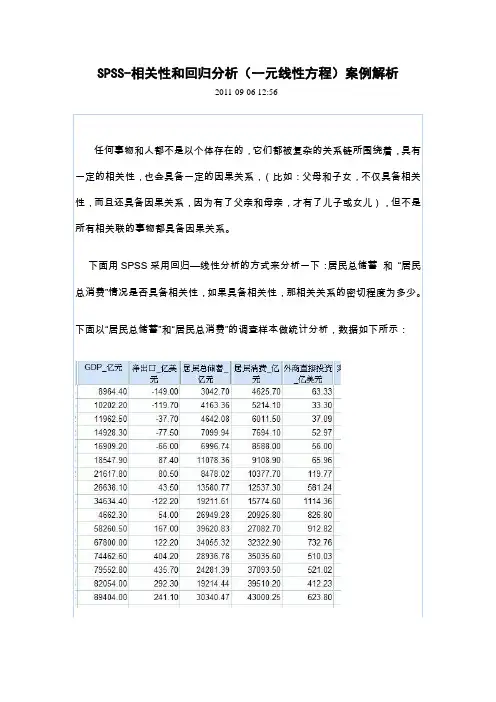
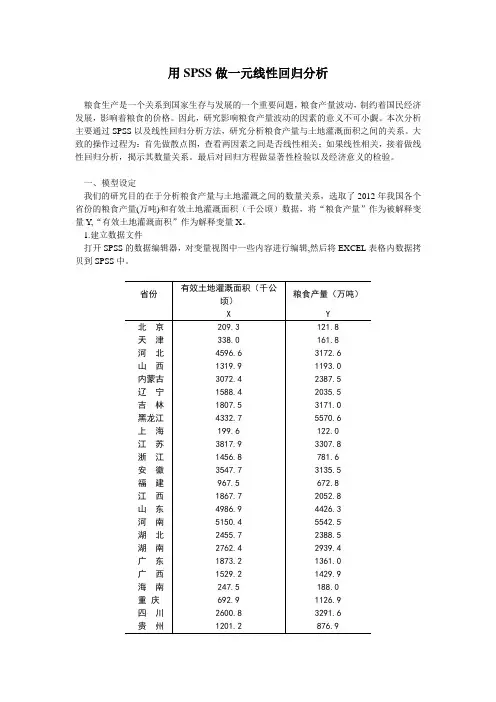
一、模型设定我们的研究目的在于分析粮食产量与土地灌溉之间的数量关系,选取了2012年我国各个省份的粮食产量(万吨)和有效土地灌溉面积(千公顷)数据,将“粮食产量”作为被解释变量Y,“有效土地灌溉面积”作为解释变量X。
1.建立数据文件打开SPSS的数据编辑器,对变量视图中一些内容进行编辑,然后将EXCEL表格内数据拷贝到SPSS中。
云南1634.2 1673.6西藏245.3 93.7陕西1274.3 1194.7甘肃1291.8 1014.6青海251.7 103.4宁夏477.6 359.0新疆3884.6 1224.7表一2.画散点图从菜单上依次点选:图形—旧对话框—散点/点状,定义简单分布,设置Y为粮食产量,X 为有效土地灌溉面积,点击确定,即可出现下面的散点图。
图一由散点图发现,粮食产量与有效土地灌溉面积之间线性相关。
所以建立如下线性模型:二、线性回归分析从菜单上依次点选:分析—回归—线性,出现线性回归对话框。
在主对话框中设置因变量为“粮食产量”,自变量为“有效土地灌溉面积”,“方法”选择默认的“进入”,即自变量一次全部进入的方法。
然后,单击右侧“保存”(注意:在“保存”中被选中的项目,都将在数据编辑窗口显示),在出现的界面中勾选95%的置信区间单值,未标准化残差。
最后,关于“统计量”,在默认情况下有“估计”和“模型拟合度”复选框被选中,再勾选“R方变化”复选框。
上述操作完成后,单击确定。

spss一元回归分析详细操作与结果分析Case1:降水&纬度Case1数据说明:⏹53个台站的年降水量、年蒸发量、纬度和海拔数据⏹在本例中,把降水量P作为因变量,纬度作为自变量Case1目的:⏹分析降水量和纬度之间的数量关系Case1操作要点:⏹做散点图,查看两因素之间是否线性相关⏹如果线性相关,接着做线性回归分析,揭示其数量关系⏹对回归方程做显著性检验打开spss的数据编辑器,编辑变量视图注意:因为我们的数据中“台站名”最多是5个汉字,所以字符串宽度最小为10才能全部显示。
编辑数据视图,将excel数据复制粘贴到spss中⏹从菜单上依次点选:图形—旧对话框—散点/点状⏹定义简单分布,设置Y为年降水量,X为纬度⏹由散点图发现,降水量与纬度之间线性相关给散点图添加趋势线的方法:•双击输出结果中的散点图•在“图表编辑器”的菜单中依次点击“元素”—“总计拟合线”,由此“属性”中加载了“拟合线”•拟合方法选择“线性”,置信区间可以选95%个体,应用step3:线性回归分析⏹从菜单上依次点选:分析—回归—线性⏹设置:因变量为“年降水量”,自变量为“纬度”⏹“方法”:选择默认的“进入”,即自变量一次全部进入的方法。
⏹“统计量”:•勾选“模型拟合度”,在结果中会输出“模型汇总”表•勾选“估计”,则会输出“系数”表⏹“绘制”:在这一项设置中也可以做散点图⏹“保存”:•注意:在保存中被选中的项目,都将在数据编辑窗口显示。
•在本例中我们勾选95%的置信区间单值,未标准化残差⏹“选项”:只需要在选择方法为逐步回归后,才需要打开【统计量】按钮⏹“回归系数”复选框组:定义回归系数的输出情况•勾选“估计”可输出回归系数B及其标准误差,t值和p值•勾选“误差条图的表征”则输出每个回归系数的95%可信区间•勾选“协方差矩阵”则会输出各个自变量的相关矩阵和方差、协方差矩阵。
⏹“残差”复选框组:•用于选择输出残差诊断的信息,可选的有Durbin-Watson残差序列相关性检验、个案诊断。



实验报告四.spss一元线性相关回归分析预测
本实验使用spss 17.0软件,针对50个被试者,使用一元线性相关回归分析预测变
量X和Y的关系。
一、实验目的
通过一元线性相关回归分析,预测50个被试者的被试变量X(会计实操次数)和被试变量Y(综合评价分)之间的关系,来检验变量X是否能够预测变量Y的值。
二、实验流程
(2)数据收集:通过收集50个被试者的实际实操次数与综合评价分,建立反映这两
者之间关系的一元线性回归方程。
(3)数据分析:通过SPSS软件的一元线性相关回归分析预测变量X和Y的关系,使
用R方值进行检验研究结果的显著性。
以分析变量X对于变量Y的影响程度。
三、实验结果及分析
1.回归分析结果如下所示:变量X的系数b = 0.6755,t = 7.561,p = 0.000,说
明变量X和被试变量Y之间存在着显著的相关关系;R方值为0.941,说明变量X可以较
好地预测变量Y。
2.可以得出一元线性回归方程为:Y=0.67×X+5.293,其中,b为系数,X是自变量,Y是因变量。
四、结论
(1)50个被试者实际实操次数与综合评价分之间存在着显著的相关性;
(2)变量X可以较好地预测变量Y,R方值较高;。

回归分析例题SPSS求解过程(一)1、一元线性回归SPSS求解过程:判别:xy202.0173.2ˆˆˆ1+=+=ββ,且x与y的线性相关系数为R=0.951,回归方程的F检验值为75.559,对应F值的显著性概率是0.000<0.05,表示线性回归方程具有显著性,当对应F值的显著性概率>0.05,表示回归方程不具有显著性。
每个系数的t检验值分别是3.017与8.692,对应的检验显著性概率分别为:0.017(<0.05)和0.000(<0.05),即否定0H,也就是线性假设是显著的。
二、一元非线性回归SPSS求解过程:1、Y与X的二次及三次多项式拟合:所以,二次式为:2029.07408.00927.6xxY-+=三次式为:320046.01534.07068.1118.4xxxY+-+=2、把Y与X的关系用双曲线拟合:作双曲线变换:xVyU1,1==判别:V U 131.0082.0-=,x V y U 1,1==,V 与U 的相关系数为R=0.968,回归方程系数的F 检验值为196.227,对应F 值的显著性概率是0.000(<0.05),表示线性回归方程具有显著性 ,每个系数的t 检验值分别是440514与14.008,对应的检验显著性概率分别为:0.000(<0.05)和0.000(<0.05),即否定0H ,也就是线性假设是显著的。
3、把Y 与X 的关系用倒指数函数拟合:x bae Y =,则x b a Y 1ln ln +=令U1=LN (Y ),V1=V=1/x,有 U1=c+bV1.判别:V U 111.1458.21-=,x V y U /1,ln 1==,V 与1U 的相关系数为R=0.979,回归方程的F 检验值为303.190,对应F 值的显著性概率是0.000(<0.05),表示线性回归方程具有显著性 ,每个系数的t 检验值分别是195.221与-17.412,对应的检验显著性概率分别为:0.000(<0.05)和0.000(<0.05),即否定0H ,也就是线性假设是显著的。
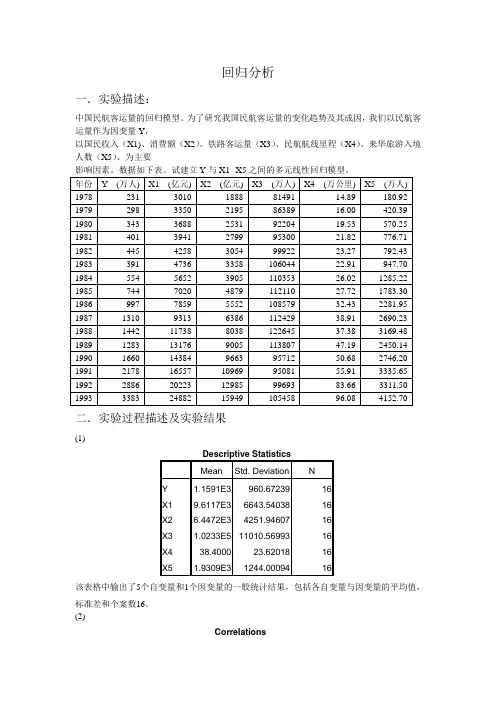
回归分析一.实验描述:中国民航客运量的回归模型。
为了研究我国民航客运量的变化趋势及其成因,我们以民航客运量作为因变量Y,以国民收入(X1)、消费额(X2)、铁路客运量(X3)、民航航线里程(X4)、来华旅游入境人数(X5)、为主要影响因素。
数据如下表。
试建立Y与X1--X5之间的多元线性回归模型。
二.实验过程描述及实验结果(1)该表格中输出了5个自变量和1个因变量的一般统计结果,包括各自变量与因变量的平均值,标准差和个案数16。
该表格中列出了各个变量之间的相关性,从该表格可以看出因变量Y和自变量X1之间的相关系数为0.989,相关性最大,。
因变量Y与自变量X3之间相关系数为0.227,相关性最小。
(3)该表格输出的是被引入或从回归方程中被剔出的各变量。
说明进行线性回归分析时所采用的方法是全部引入法Enter。
因变量为Y。
(4)该表格输出的是常用统计量。
从该表看出相关性系数R为0.999,判定系数R2为0.998,调整的判定系数为0.997,回归估计的标准误差为49.49240。
该表格输出的是方差分析表。
从这部分结果看出:统计量F为1.128E3;相伴概率值小于0.01,拒绝原假设说明多个自变量与因变量Y之间存在线性回归关系。
Sum of Squares一栏中分别代表回归平方和(1.382E7),残差平方和(24494.981)以及总平方和(1.384E7),df为自由度。
判定系数R2=0.99855。
该表格为回归系数分析。
其中Unstandardized Coefficients为非标准化系数,Standardized Coefficients为标准化系数,t为回归系数检验统计量,sig为相伴概率值。
由表知t检验的相伴概率值均小于0.01,拒绝原假设,说明个变量与因变量之间均有显著线性相关关系。
从表格中可以看出该多元线性回归方程为:y=450.909+0.354 X1-0.561 X2-0.007 X3+21.578 X4+0.435 X5该表格为残差统计结果表。

用下面的数据做相关分析和一元线性回归分析:选用普通高等学校毕业生数和高等学校发表科技论文数量做相关分析和一元线性回归分析。
一、相关分析1.作散点图普通高等学校毕业生数和高等学校发表科技论文数量的相关图从散点图可以看出:普通高等学校毕业生数和高等学校发表科技论文数量的相关性很大。
2.求普通高等学校毕业生数和高等学校发表科技论文数量的相关系数把要求的两个相关变量移至变量中,因为都是定距数据,选择相关系数中的Pearson,点击确定,可以得到下面的结果:关;相关系数检验对应的概率P值=0.000,小于显著性水平0.05,应拒绝原假设(两变量之间不具有相关性),即毕业生人数好发表科技论文数之间的相关性显著。
3.求两变量之间的相关性选择相关系数中的全部,点击确定:Correlations(万人) (篇)Kendall's tau_b (万人)CorrelationCoefficient1.000 1.000** Sig. (2-tailed) . .N 14 14 (篇) CorrelationCoefficient1.000**1.000Sig. (2-tailed) . .N 14 14Spearma n's rho (万人)CorrelationCoefficient1.000 1.000**Kendall相关系数=1.000,呈正相关;无相关系数检验对应的概率P 值,应接受原假设(两变量之间不具有相关性),即毕业生数与发表论文数之间相关性不显著。
两相关变量(毕业生数和发表论文数)的Spearman 相关系数=1.000,呈正相关;无相关系数检验对应的概率P值,应接受原假设(两变量之间不具有相关性),即毕业生数与发表论文数之间相关性不显著。
4.普通高等学校毕业生数和高等学校发表科技论文数量的相关系数将所求变量移至变量,将控制变量移至控制中,选中显示实际显著性水平,点击确定:Correlations相关系数=0.998,呈正相关;对应的偏相关系数双侧检验p 值0,小于显著性水平0.05,应拒绝原假设(两变量之间不具有相关性),即普通高校毕业生数与发表论文数之间相关性显著。

用下面的数据做相关分析和一元线性回归分析:选用普通高等学校毕业生数和高等学校发表科技论文数量做相关分析和一元线性回归分析。
一、相关分析1.作散点图普通高等学校毕业生数和高等学校发表科技论文数量的相关图从散点图可以看出:普通高等学校毕业生数和高等学校发表科技论文数量的相关性很大。
2.求普通高等学校毕业生数和高等学校发表科技论文数量的相关系数把要求的两个相关变量移至变量中,因为都是定距数据,选择相关系数中的Pearson,点击确定,可以得到下面的结果:Correlations普通高等学校毕业生数(万人)高等学校发表科技论文数量(篇)普通高等学校毕业生数(万人)PearsonCorrelation1.998** Sig. (2-tailed).000 N1414高等学校发表科技论文数量(篇)PearsonCorrelation.998**1 Sig. (2-tailed).000N1414Correlations普通高等学校毕业生数(万人)高等学校发表科技论文数量(篇)普通高等学校毕业生数(万人)PearsonCorrelation1.998** Sig. (2-tailed).000 N1414高等学校发表科技论文数量(篇)PearsonCorrelation.998**1 Sig. (2-tailed).000N1414**. Correlation is significant at the 0.01 level(2-tailed).两相关变量的Pearson相关系数=0.0998,表示呈高度正相关;相关系数检验对应的概率P值=0.000,小于显着性水平0.05,应拒绝原假设(两变量之间不具有相关性),即毕业生人数好发表科技论文数之间的相关性显着。
3.求两变量之间的相关性选择相关系数中的全部,点击确定:Correlations(万人)(篇)Kendall's tau_b (万人)CorrelationCoefficient1.000 1.000**Sig. (2-tailed)..N1414 (篇)CorrelationCoefficient1.000** 1.000Sig. (2-tailed)..N1414Spearman's rho (万人)CorrelationCoefficient1.000 1.000**Sig. (2-tailed)..N1414 (篇)CorrelationCoefficient1.000** 1.000Sig. (2-tailed)..N1414**. Correlation is significant at the 0.01 level(2-tailed).注解:两相关变量(毕业生数和发表论文数)的Kendall相关系数=1.000,呈正相关;无相关系数检验对应的概率P值,应接受原假设(两变量之间不具有相关性),即毕业生数与发表论文数之间相关性不显着。