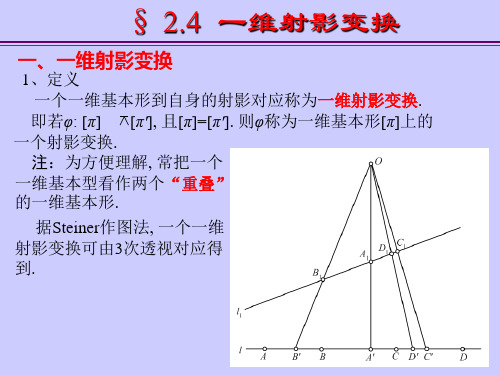
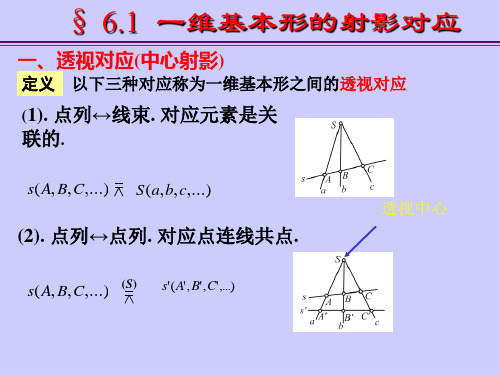
高等几何讲义 第三章 射影变换____§1 一维射影变换

第三讲射影几何与射影空间一、射影几何的起源与确立射影几何是研究图形的射影性质，即经过射影变换后，依然保持图形性质不变的几何学分支。

射影几何也叫投影几何学，通过它可以把欧氏几何、仿射几何等联系起来。

射影几何的某些内容在公元前就已经出现了，基于绘图学和建筑学的需要，古希腊几何学家就开始研究透视法，也就是投影和截影。

早在公元前200年左右，阿波罗尼奥斯就曾把二次曲线作为正圆锥面的截线来研究。

在4世纪帕普斯的著作中，出现了帕普斯定理。

但射影几何直到十九世纪才形成独立体系，趋于完备。

1.达·芬奇（1452—1519）射影几何的最早起源是绘画。

达·芬奇是一位思想深邃，学识渊博，多才多艺的画家、发明家、哲学家、音乐家、医学家、建筑和军事工程师。

他广泛地研究与绘画有关的光学、数学、地质学、生物学等多种学科。

在《绘画专论》一书中，他对透视法作了详尽的论述。

他的代表作《最后的晚餐》是基督教传说中最重要的故事。

这幅画就是严格采用透视法的。

在数学方面，他巧妙地用圆柱滚动一周的方法解决了化圆为方的难题，另外他还研究过等腰梯形、圆内接多边形的作图，四面体的重心等。

此外，达·芬奇还发现了液体压力的概念，提出了连通器原理。

达·芬奇在生理解剖学上也取得了巨大的成就，被认为是近代生理解剖学的始祖。

他绘制了比较详细的人体解剖图。

在建筑方面，达·芬奇也表现出了卓越的才华。

他设计过桥梁、教堂、城市街道和城市建筑。

达·芬奇的研究和发明还涉及到了军事领域。

他发明了簧轮枪、子母弹、三管大炮、坦克车、浮动雪鞋、潜水服及潜水艇、双层船壳战舰、滑翔机、直升飞机和旋转浮桥等。

看过《达·芬奇密码》的人大概都知道达·芬奇密码筒。

达·芬奇设计的这种密码筒造型古典，内涵着文艺复兴特质，设计优雅。

要打开密码筒，必须解开一个5位数的密码，密码筒上有5个转盘，每个转盘上都有26个字母，可能作为密码的排列组合多达11881376种。

射影变换4.1 点列和线束点列和线束定义．两个矢量),,(321a a a 和),,(321b b b 表示不同的点当且仅当这两个矢量线性无关． 在两点A ),,(321a a a 与B ),,(321b b b 的连线上任意一点),,(321x x x X 满足0321321321=b b b a a a x x x即，三点A ),,(321a a a ，B ),,(321b b b 与),,(321x x x X 共线的充分必要条件是0321321321=b b b a a a x x x以B A ,为基点的点列中，任何一点X 都可以表示为B A X μλ+=，用齐次坐标可以表示为B A B A X λλμ'+=+=；以m l ,为基线的线束中，任何一直线p 都可以表示为m l p μλ+=，用齐次坐标可以表示为m l m l p λλμ'+=+=．练习4－1１．已知A 和B 的齐次坐标分别为)1,1,5(和)1,0,1(-，求直线AB 上一点C ，使1)(-=ABC ，若B A C λ+=，求出λ．解利用非齐次坐标),(y x 与齐次坐标),,(321x x x 之间的关系31x x x =，32x xy =．这时，)1,5(),(=y x A ，)0,1(),(-=y x B ，再利用BC AC ABC =)(．115-=+-x x ，解得2=x，101-=--y y ，解得21=y ．即)21,2(=C ，C 点的齐次坐标为)1,21,2(． 因为B A C 2121+=，所以 1=λ． 注意：以B A ,为基点的点列中，任何一点X 都可以表示为B A X μλ+=，用齐次坐标可以表示为B A B A X λλμ'+=+=． ２．试证明：三点),,(321x x x ，),,(321y y y ，),,(321z z z 共线的充分必要条件为0321321321=z z z y y y x x x 证明三点),,(321x x x ，),,(321y y y ，),,(321z z z 共线的充分必要条件为λ=--=--=--333322221111y z x z y z x z y z x z所以0332211321332211321321321=-------=y z y z y z y y y x z x z x z z z z y y y x x x４．已知直线0143=++y x 与02=+y x ，求过两直线的交点与点)0,1,2(的直线方程．解两直线0143=++y x 与02=+y x 的交点为)5,1,3(112143321--=x x x 于是点)5,1,3(--与点)0,1,2(的直线方程为05105012513321321=+-=--x x x x x x即05105321=+-x x x ．4.2 点列和线束的交比定义4.2设D C B A ,,,为点列上共线的四点，则这四点的交比为ADBC BDAC CD AB ⋅⋅=),(．定理 4.１取A 和B 为基点，将D C B A ,,,四点的坐标依次表示为a ，b ，b a 1λ+，b a 2λ+，则四点的交比为21),(λλ=CD AB ． 定理4.２若D C B A ,,,四点的坐标为)4,3,2,1(21=+i P P i λ，21,P P 点列上两个基点，则),(),(432124142313λλλλλλλλλλλλ=----=CD AB定理4.３将某两点互换，同时互换其余两点，则交比不变．即),(),(),(),(BA DC AB CD DC BA CD AB ===定理4.４只在一对点中互换，交比转为其倒数．即),(1),(CD AB DC AB =，),(1),(CD AB CD BA =定理4.５交换中间两点，则交比为１与原值的差，即),(1),(CD AB BD AC -= 定义4.３当1),(-=CD AB 时，称D C ,调和分割线段AB ．调和分割的关系是对等的．因为1),(),(-==CD AB AB CD ，所以，B A ,也调和分割线段CD ，有时也称D C B A ,,,为调和点列．定义4.４称21λλ为四直线d c b a ,,,的交比，记为),(cd ab ．即 =),(cd ab 21λλ．注意：用齐次坐标之间的关系定义交比，点列的交比与线束的交比在形式上完全一致．定理4.６设四直线d c b a ,,,，若b a c 1λ+=，b a d 2λ+=，则=),(cd ab 21λλ． 定理4.7若四直线q p a 1μ+=，q p b 2μ+=，q p c 3μ+=，q p d 4μ+=，则 424132314321),(),(μμμμμμμμμμμμ----==cd ab ．这个比值也称为数4321,μμμμ的交比．定理4.８两个点列经过中心投影，交比不变．练习4－2１． 设E D C B A ,,,,是同一直线上的五点，求证1),)(,)(,(=EC AB DE AB CD AB ．证明由交比定义ADBC BDAC CD AB ⋅⋅=),(，1),)(,)(,(=⋅⋅⋅⋅⋅⋅⋅⋅=ACBE BCAE AE BD BE AD AD BC BD AC EC AB DE AB CD AB ．２．设C B A ,,三点的坐标分别为)1,1,1(，)1,1,1(-，)1,0,1(，且2),(=CD AB ，求点D 的坐标．解)1,1,1(=A ，)1,1,1(-=B ，则C B A ==+)1,0,1(2121，于是12=λ．设B A D 1λ+=，由2),(21==λλCD AB 可知，21=λ，所以)3,1,3(2-=+=B A D ．注意：以B A ,为基点的点列中，任何一点X 都可以表示为B A X μλ+=，用齐次坐标可以表示为B A B A X λλμ'+=+=． ３．求四点)1,1,2(-A ，)1,1,1(-B ，)0,0,1(C ，)5,5,1(-D 的交比),(CD AB ．解利用定理 4.1，取A 和B 为基点，将D C B A ,,,四点的坐标依次表示为a ，b ，b a 1λ+，b a 2λ+，则四点的交比为21),(λλ=CD AB ． 这里B AC +=，于是11=λ， B AD 32-=，于是232-=λ，由21),(λλ=CD AB 可知，32),(21-==λλCD AB ． 注意：以B A ,为基点的点列中，任何一点X 都可以表示为B A X μλ+=，用齐次坐标可以表示为B A B A X λλμ'+=+=． ７．试证：02321=+-x x x ，023321=-+x x x ，0721=-x x ，0531=-x x 所表示的四直线共点，并求这四直线的交比．解直线0721=-x x 与0531=-x x 的交点为)5,7,1(15017321=--x x x 点)5,7,1(满足四直线，所以，此四直线共点． 四直线与x 轴的交点分别为211-=x ，322=x ，03=x ，514=x ，所以，21),(4321=l l l l ．4.3 完全四点形和完全四线形完全四点形和完全四线形定义．定理4.6完全四点形通过每一个对角点有一组调和线束，即通过这个对角点的两边和对角三角形的两边．定理4.10完全四线形的每一条对角线上有一组调和点列，即这条直线上的两个顶点及对角三角形的两个顶点．练习4－3２．设XYZ 是完全四点形ABCD 的对边三点形，XY 分别交BD AC ,于M L ,，不用笛沙格定理，证明CM BL YZ ,,共点．证明由四点形ABCD ，根据定理可知，在AC 边上的四点L Y C A ,,,调和共轭， 即1),(-=YL AC ．在四点形YBZL 中，LB 与YZ 交于N ，MN 与YL 交于C '，由定理可得),(-='YL CA 所以，点C 应与点C '重合，即CM BL YZ ,,共点．4.4 一维基本图形的射影对应两个点列成射影对应的定义． 两个线束成射影对应的定义． 点列与线束成射影对应的定义．定理4.11 设两个一维基本图形成射影对应，则对应四元素的交比相等． 定理4.12 若两个一维基本图形对应四个元素的交比相等，则必成射影对应． 定理 4.13 如果已知两个一维图形的任意三对对应元素，那么可以确定唯一一个射影对应．练习4－4５． 若三角形ABC 的三边AB 、BC 、C A 分别通过共线的三点P ，Q ，R ，二顶点B 与C 各在定直线上，求证顶点A 也在一条直线上．证明根据图形(见第４题图)可知，题图）（第2Λ),,,(21ΛB B B ),,,(21ΛC C C ，则Λ),,,(21ΛB B B P ),,,(21ΛC C C R在这两个射影线束中，PR是自对应元素，所 以Λ),,,(21ΛB B B P ),,,(21ΛC C C R两透视对应的线束对应直线的交点Λ,,,21A A A 共线． 4.5 透视对应定义4.8点列和线束成射影对应，如果对应直线过对应点，这种特殊的射影对应称为透视对应，这时也这两个一维图形处于透视状态．定义4.9两个点列和同一个线束成透视对应，也就是说两个点列成中心射影对应，则称这两个点列成透视对应．定义4.10两个线束和同一个点列成透视对应，则称这两个线束成透视对应． 定理4.14两个射影对应的点列成透视的充要条件是：两个点列的公共点自对应． 定理4.15两个射影对应的线束成透视的充要条件是：两个线束的公共点自对应． 定理4.16(巴卜斯定理)设C B A ,,是直线l 上互异的三点，C B A ''',,是l '上互异的三点，那么三个交点C B C B L '⨯'=，B A B A N '⨯'=，A C A C M '⨯'=共线．定理4.17对于两个不共底的且不成透视对应的射影对应点列，用两次透视对应，可把第一个点列变成第二个点列．也就是说，射影对应是两个透视对应的复合．定理4.18设一个点列与一个线束成射影对应而不成透视对应，那么用三次透视就可以彼此转换．即，这时的射影对应是三个透视对应的复合．题图）（第5A１．如图四边形ABCD 被EF 分成两个四边形AFED 和FBCE ，求证三个四边形ABCD ，AFED ，FBCE 的对角线交点H G K ,,共线．证明因为D ，E ，C 直线l 上互异的三点，A ，F ，B 是直线m 上互异 的三点，由定理4.16（巴卜斯定理），三个交点AE DF G⨯=，AC DB K ⨯=， FC EB H ⨯=共线．4.6 对合对应对合对应定义．定理4.19两个重叠的一维图形（点列、线束）q p μ+，q p μ'+成为对合对应的充分必要条件是：对应元素的参数μ和μ'满足0)(=+'++'d b a μμμμ其中02≠-b ad ．定理4.20不重合的两对对应元素，确定唯一一个对合对应．１．求参数为21→，20→的两对对应元素所确定的对合对应． 解利用定理 4.19，这里两对对应元素的参数μ和μ'分别为21,1='=μμ和2,0='=μμ，设0)(=+'++'d b a μμμμ为所求的对合对应，把两对对应参数值代入得）题图（第1DAFBCEGKHlm⎪⎩⎪⎨⎧=+=++0202321d b d b a 解得2:1:1::-=d b a ，因此，这两对对应元素所确定的对合对应为02=-'++'μμμμ．。