一维射影变换

第三章 射影变换与射影坐标本章首先引入射影不变量——交比。

然后在此基础上，讨论了一维基本形之间的射影对应与射影变换，以及二维射影对应和射影变换，还定义了一维和二维射影坐标。

§1 交比与调和比点列中四点的交比与调和比定义1.1 共线的四个不同点A ，B ，C ，D 的交比等于单比（ABC ）与单比（ABD ）的比，记作：（AB ，CD ），即（AB ，CD ）=)()(ABD ABC其中A ，B 叫基点偶，C ，D 叫分点偶。

交比又称交叉比和复比。

由交比和单比的定义，我们可AD BC BDAC BDAD BC ACABD ABC CD AB ⋅⋅===)()()(， 其中AC ，BC ，AD ，BD 是有向线段的数量。

我们不难得出：（1） 点偶C ，D 不分离点偶A ，B 时，交比（AB ，CD ）﹥0； （2） 点偶C ，D 分离点偶A ，B 时，交比（AB ，CD ）﹤0； （3） 当C ，D 重合时，（AB ，CD ）=1； （4） 当A ，C 重合时，（AB ，CD ）=0。

定理1.1 基点偶与分点偶交换，交比值不改变，即 （AB ，CD ）=（CD ，AB ） 证明 由定义1.1，（CD ，AB ）=),(CD AB BCAD BDAC CB DA DB CA =⋅⋅=⋅⋅ 定理1.2 基点偶的两个字母交换或分点偶的两个字母交换，交比的值变成原来的交比值的倒数，即（BA ，CD ）=（AB ，DC ）=),(1CD AB证明（AB ，DC ）=),(1)()(1)()(CD AB ABD ABC ABC ABD == 又（BA ，CD ）=（CD ，BA ）=),(1),(1CD AB AB CD =推论 同时交换每个点偶里的字母，交比的值不改变，即 （AB ，CD ）=（BA ，DC ） 定理1.3 交换中间的两个字母或两端的两个字母，交比的值等于1减去原来的交比值，即（AC ，BD ）=（DB ，CA ）=1－（AB ，CD ）证明（AC ，BD ）AD CB CD AB ⋅⋅=AD CB BD CB BC AC ⋅++=))(( AD CB BDAC CB BD CB AC ⋅⋅+++=)(AD CB BD AC ⋅⋅+=1=1+)(ADBC BDAC ⋅⋅-=1－（AB ，CD ）共线四点1，2，3，4一共有4！=24中不种的排列，所以有24个交比，根据交比的运算性质，它们只有6个不同的交比值，即（12，34）=（34，12）=（21，43）=（43，21）=m（21，34）=（34，21）=（12，43）=（43，12）=m1（13，24）=（24，13）=（31，42）=（42，31）=1－m（13，42）=（42，13）=（31，24）=（24，31）=m-11（14，23）=（23，14）=（41，32）=（32，41）=1－m 1（14，32）=（32，14）=（41，23）=（23，41）=1-m m例1 已知（P 1P 2，P 3P 4）=3，求（P 4P 3，P 2P 1）和（P 1P 3，P 2P 4）的值解 （P 4P 3，P 2P 1）= （P 2P 1 ，P 4P 3）=（P 1P 2，P 3P 4）=3 （P 1P 3，P 2P 4）=1－（P 1P 2，P 3P 4）=1－3=－2下面研究交比的代数表示定理1.4 一直线上的无穷远点分其上任何两点的单比等于1。

《高等几何》课程学习指南一、课程目的本课程是大学数学类专业的主干基础课程之一。

本课程在大家具备初等几何、解析几何、高等代数、数学分析知识的基础上，系统地学习射影几何的基本知识，使我们能用变换群的观点来看待几何学，加深对几何学的理解，拓展几何空间概念。

通过本课程利用商空间思想研究亏格为零不可定向的闭曲面上的几何学的训练，一方面使得我们拓宽眼界，扩大知识领域，提高抽象思维、理性思维能力，为进一步的数学学习打下基础；另一方面使得我们加深对中学几何特别是解析几何的理论与方法的理解，从而获得用高观点来处理中学几何问题的能力，为未来的中学几何教学打下基础；第三，本课程包括了许多著名的定理，奇妙的图形，匪夷所思的处理技巧，通过本课程的学习，可以有效地提高我们的数学审美意识。

概括来说，学习本课程后，希望大家有如下收获：（1）空间不只是平直的，除欧氏空间外，还有很多其他的空间。

即让学生在空间观念上有一个提升；（2）进一步让了解处理几何问题不只是可以用综合法，还可以用解析法；（3）深刻理解对偶原理，认识到射影几何是与欧氏几何完全不同的几何学；（4）深刻理解射影变换及其性质，认识到射影几何是研究射影图形在射影变换下的不变性和不变量的一门科学；（5）深刻理解Klein的变换群观点，即研究某空间中的图形在它的某变换群作用下不变的性质和数量的科学就称为一门几何学；（6）深刻了解一些平面射影图形的射影性质。

如：点列，线束，完全n点（线）形，二次曲线的射影性质。

（7）学会构造射影图形。

因为我们的纸张是欧氏平面，所以在其上构造射影图形还是有很多技巧，我们要深刻领会这些技巧。

二、课程主要内容结构以平面射影几何为主体，涵盖射影几何，变换群理论，仿射几何等内容，主要包括5个部分：1、射影平面。

包括引论，拓广平面，齐次点坐标，线坐标，射影平面，对偶原则，复元素，Desargues定理等。

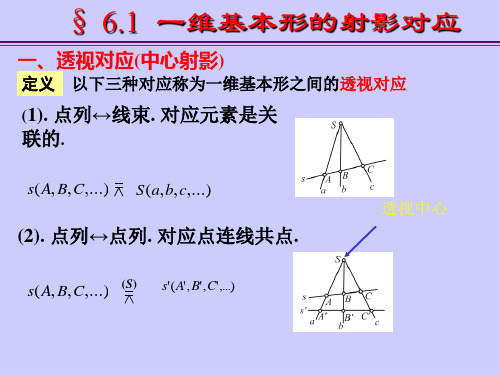
2、射影变换。

包括交比与调和比，完全四点形与完全四线形的调和性，一维基本形的射影对应，一维射影变换，一维基本形的对合，二维射影变换等。

高等几何_南京师范大学中国大学mooc课后章节答案期末考试题库2023年1.一维射影变换是答案:椭圆型对合2.两个点列之间的射影对应是由答案:三对对应点唯一确定3.已知共线四点的交比, 则交比答案:4.点的齐次线坐标方程为答案:5.以下四条直线上的无穷远点与其他三条上无穷远点不同的是答案:6.射影平面上，三条互异直线最多把平面划分为个不同部分答案:7.已知共线四点A,B,C,D 是一个调和点组，任意调整四点顺序所得交比不会出现的是答案:8.仿射几何的基本不变量是答案:单比9.射影几何的基本不变量是答案:交比10.二次曲线的射影分类总共可分为类。

答案:511.两射影线束，，生成的二阶曲线方程为.答案:正确12.圆的任意一条切线截其四条相异的定切线所得截点的交比是定值。

答案:正确13.非退化二阶曲线的任一内接三点形每一顶点处的切线与对边的交点三点必共线.答案:正确14.设为非退化有心二阶曲线的两条直径，又为其两条渐近线，则为的一对互异共轭直径当且仅当。

答案:正确15.在射影仿射平面上，非退化二阶曲线为椭圆的充要条件是其与无穷远直线相切。

答案:错误16.直线关于二阶曲线的极点坐标为。

答案:错误17.直线是非退化二阶曲线的直径的充要条件是关于的极点为无穷远点。

答案:错误18.在射影平面上，一条二阶曲线上必有无三点共线的相异五点。

答案:错误19.两个不同底的成射影对应的点列对应点的连线的集合构成一条非退化二级曲线。

答案:错误20.两个不同束心的成射影对应的线束对应直线的交点的集合构成一条二阶曲线。

答案:正确21.在射影仿射平面上，任一非退化二阶曲线皆有两条相异的渐近线。

答案:错误22.非退化二阶曲线的任一外切简单四线形的两条对角线和两组对边上的切点的连线必共点。

答案:正确23.对射影仿射平面上的二阶曲线，若，则二阶曲线为椭圆。

答案:错误24.平面上任意五点可确定唯一一条非退化二阶曲线。

答案:错误25.平面上五条直线（其中无三线共点）可确定唯一一条非退化二级曲线。