图论实现邻接矩阵实验报告C语言
- 格式:doc
- 大小:72.50 KB
- 文档页数:4

一、实验目的1. 理解传递闭包的概念及其在图论中的应用。
2. 掌握利用Floyd-Warshall算法求解传递闭包的方法。
3. 通过编程实现传递闭包的计算,验证算法的正确性。
4. 分析实验结果,加深对传递闭包性质的理解。
二、实验原理传递闭包是指在给定集合X上的二元关系R,找到一个最小的传递关系R,使得对于任意的x, y, z∈X,若xRy且yRz,则xRz成立。
传递闭包可以用来描述图中节点之间的可达性,是图论中一个重要的概念。
Floyd-Warshall算法是一种求解传递闭包的经典算法,它通过构建一个n×n的邻接矩阵A,其中A[i][j]表示节点i到节点j的可达性。
算法的基本思想是:逐步更新矩阵A,使得A[i][j]的值表示节点i到节点j的最短路径可达性。
三、实验内容1. 设计一个图,包括节点和边,并构建相应的邻接矩阵。
2. 利用Floyd-Warshall算法计算邻接矩阵的传递闭包。
3. 分析传递闭包的结果,验证算法的正确性。
4. 对比不同图结构下的传递闭包计算结果,探讨传递闭包的性质。
四、实验步骤1. 设计一个图,包括5个节点和6条边,如下所示:```1 -- 2| || |3 -- 4| || |5 -- 6```2. 构建邻接矩阵A,如下所示:```| 1 2 3 4 5 6 |1| 0 1 0 0 0 0 |2| 0 0 1 0 0 0 |3| 0 0 0 1 0 0 |4| 0 0 0 0 1 0 |5| 0 0 0 0 0 1 |6| 0 0 0 0 0 0 |```3. 编写Floyd-Warshall算法的代码,计算传递闭包。
```pythondef floyd_warshall(adj_matrix):n = len(adj_matrix)for k in range(n):for i in range(n):for j in range(n):if adj_matrix[i][j] > adj_matrix[i][k] + adj_matrix[k][j]:adj_matrix[i][j] = adj_matrix[i][k] + adj_matrix[k][j]return adj_matrix# 初始化邻接矩阵adj_matrix = [[0, 1, 0, 0, 0, 0],[0, 0, 1, 0, 0, 0],[0, 0, 0, 1, 0, 0],[0, 0, 0, 0, 1, 0],[0, 0, 0, 0, 0, 1],[0, 0, 0, 0, 0, 0]]# 计算传递闭包transitive_closure = floyd_warshall(adj_matrix) print(transitive_closure)```4. 分析传递闭包的结果,验证算法的正确性。


数据结构实验报告一、实验目的数据结构是计算机科学中非常重要的一门课程,通过本次实验,旨在加深对常见数据结构(如链表、栈、队列、树、图等)的理解和应用,提高编程能力和解决实际问题的能力。
二、实验环境本次实验使用的编程语言为C++,开发工具为Visual Studio 2019。
操作系统为 Windows 10。
三、实验内容1、链表的实现与操作创建一个单向链表,并实现插入、删除和遍历节点的功能。
对链表进行排序,如冒泡排序或插入排序。
2、栈和队列的应用用栈实现表达式求值,能够处理加、减、乘、除和括号。
利用队列实现银行排队系统的模拟,包括顾客的到达、服务和离开。
3、二叉树的遍历与操作构建一棵二叉树,并实现前序、中序和后序遍历。
进行二叉树的插入、删除节点操作。
4、图的表示与遍历用邻接矩阵和邻接表两种方式表示图。
实现图的深度优先遍历和广度优先遍历。
四、实验步骤及结果1、链表的实现与操作首先,定义了链表节点的结构体:```cppstruct ListNode {int data;ListNode next;ListNode(int x) : data(x), next(NULL) {}};```插入节点的函数:```cppvoid insertNode(ListNode& head, int val) {ListNode newNode = new ListNode(val);head = newNode;} else {ListNode curr = head;while (curr>next!= NULL) {curr = curr>next;}curr>next = newNode;}}```删除节点的函数:```cppvoid deleteNode(ListNode& head, int val) {if (head == NULL) {return;}ListNode temp = head;head = head>next;delete temp;return;}ListNode curr = head;while (curr>next!= NULL && curr>next>data!= val) {curr = curr>next;}if (curr>next!= NULL) {ListNode temp = curr>next;curr>next = curr>next>next;delete temp;}}```遍历链表的函数:```cppvoid traverseList(ListNode head) {ListNode curr = head;while (curr!= NULL) {std::cout << curr>data <<"";curr = curr>next;}std::cout << std::endl;}```对链表进行冒泡排序的函数:```cppvoid bubbleSortList(ListNode& head) {if (head == NULL || head>next == NULL) {return;}bool swapped;ListNode ptr1;ListNode lptr = NULL;do {swapped = false;ptr1 = head;while (ptr1->next!= lptr) {if (ptr1->data > ptr1->next>data) {int temp = ptr1->data;ptr1->data = ptr1->next>data;ptr1->next>data = temp;swapped = true;}ptr1 = ptr1->next;}lptr = ptr1;} while (swapped);}```测试结果:创建了一个包含 5、3、8、1、4 的链表,经过排序后,输出为 1 3 4 5 8 。

图的上机实验报告一、实验目的本次实验的目的是进一步了解图的概念、图的存储结构和图的遍历算法,并通过具体的上机实验来熟悉图的相关操作。
二、实验环境- 操作系统:Windows 10- 编程语言:C++- 开发环境:Visual Studio 2019三、实验内容本次实验主要包括以下几个方面的内容:1.图的基本概念首先,我们需要了解图的基本概念。
图是一种非线性的数据结构,由顶点集合和边集合构成。
顶点代表图中的一个节点,而边则代表顶点之间的关系。
图可以分为有向图和无向图,其中有向图的边是有方向的,而无向图的边是无方向的。
2.图的存储结构图的存储结构有两种常见的方式:邻接矩阵和邻接表。
邻接矩阵是用一个二维数组来表示图的结构,数组中的元素表示两个顶点之间是否有边。
邻接表则是由一个链表数组组成,每个数组元素对应一个顶点,链表中存储了与该顶点相邻的其他顶点。
3.图的遍历算法图的遍历算法有两种常见的方式:深度优先搜索(DFS)和广度优先搜索(BFS)。
深度优先搜索是从某个顶点开始,递归地访问该顶点的邻接顶点,直到无法再继续深入为止,然后回溯到之前的顶点。
而广度优先搜索是从某个顶点开始,依次访问该顶点的所有邻接顶点,然后按照同样的方式访问邻接顶点的邻接顶点,直到所有顶点都被访问完毕。
四、实验步骤根据上述内容,我们进行了如下实验步骤:1. 创建一个图对象,选择合适的存储结构(邻接矩阵或邻接表);2. 根据实际需求,添加图的顶点和边;3. 选择相应的遍历算法(DFS或BFS);4. 遍历图,输出遍历结果。
五、实验结果在实验过程中,我们成功地创建了一个图对象,并使用邻接矩阵存储了图的结构。
然后,我们添加了一些顶点和边的信息,并选择了深度优先搜索算法进行遍历。
最后,我们成功地遍历了整个图,并输出了遍历结果。
六、实验总结通过本次实验,我们进一步掌握了图的基本概念、图的存储结构和图的遍历算法。
同时,我们也了解到不同的存储结构和遍历算法在不同的应用场景中,有着各自的优缺点。
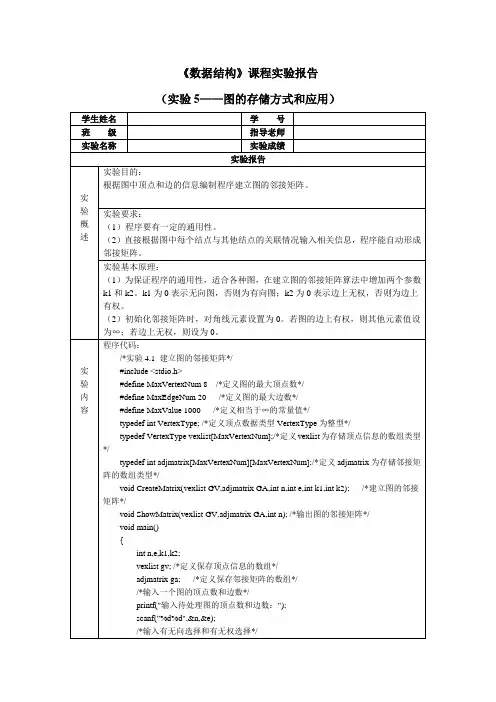


数学与计算机学院课程设计说明书课程名称: 数据结构与算法课程设计课程代码: 6014389 题目: 无向图的邻接矩阵存储结构年级/专业/班: 2010级软件4班学生姓名: 吴超学号: 312010*********开始时间: 2011 年 12 月 9 日完成时间: 2011 年 12 月 30 日课程设计成绩:指导教师签名:年月日数据结构课程设计任务书学院名称:数学与计算机学院课程代码:__6014389______ 专业:软件工程年级:2010一、设计题目无向图的邻接矩阵存储结构二、主要内容图是无向带权图,对下列各题,要求写一算法实现。
1)能从键盘上输入各条边和边上的权值;2)构造图的邻接矩阵和顶点集。
3)输出图的各顶点和邻接矩阵4)插入一条边5)删除一条边6)求出各顶点的度7)判断该图是否是连通图,若是,返回1;否则返回0.8)使用深度遍历算法,输出遍历序列。
三、具体要求及应提交的材料用C/C++语言编程实现上述内容,对每个问题写出一个算法实现,并按数学与计算机学院对课程设计说明书规范化要求,写出课程设计说明书,并提交下列材料:1)课程设计说明书打印稿一份2)课程设计说明书电子稿一份;3)源程序电子文档一份。
四、主要技术路线提示用一维数组存放图的顶点信息,二维数组存放各边信息。
五、进度安排按教学计划规定,数据结构课程设计为2周,其进度及时间大致分配如下:六、推荐参考资料[1] 严蔚敏,吴伟民.数据结构.清华大学出版社出版。
[2] 严蔚敏,吴伟民. 数据结构题集(C语言版) .清华大学出版社.2003年5月。
[3]唐策善,李龙澎.数据结构(作C语言描述) .高等教育出版社.2001年9月[4] 朱战立.数据结构(C++语言描述)(第二版本).高等出版社出版.2004年4月[5]胡学钢.数据结构(C语言版) .高等教育出版社.2004年8月指导教师签名日期年月日系主任审核日期年月日目录引言 (7)1 需求分析 (7)1.1任务与分析 (7)1.2测试数据 (8)2 概要设计 (8)2.1 ADT描述 (8)2.2程序模块结构 (9)2.3各功能模块 (11)3详细设计 (11)3.1类的定义 (11)3.2 初始化 (12)3.3 图的构建操作 (13)3.4 输出操作 (13)3.5 get操作 (14)3.6 插入操作 (14)3.7 删除操作 (15)3.8 求顶点的度操作 (15)3.10 判断连通操作 (17)3.11 主函数 (17)4 调试分析 (17)4.1 测试数据 (20)4.2调试问题 (20)4.3 算法时间复杂度 (20)4.4 经验和心得体会 (21)5用户使用说明 (21)6测试结果 (21)6.1 创建图 (21)6.2插入节点 (22)6.3 深度优先遍历 (22)6.4 求各顶点的度 (22)6.5 输出图 (23)6.6 判断是否连通 (23)6.7 求边的权值 (24)6.8 插入边 (24)6.9 删除边 (25)结论 (26)致谢 (27)摘要随着计算机的普及,涉及计算机相关的科目也越来越普遍,其中数据结构是计算机专业重要的专业基础课程与核心课程之一,为适应我国计算机科学技术的发展和应用,学好数据结构非常必要,然而要掌握数据结构的知识非常难,所以对“数据结构”的课程设计比不可少。

沈阳工程学院学生实验报告(课程名称:数据结构与算法)实验题目:图班级计算机121学号2012417116 姓名赵玉林地点F608 指导教师张欣实验日期: 2013 年11 月28 日一、实验目的1.掌握图的基本存储方法。
2.掌握有关图的操作算法并用高级语言实现。
3.熟练掌握图的两种搜索路径的遍历方法。
4.掌握图的有关应用。
二、实验环境Turbo C或是Visual C++三、实验内容与要求实验1 建立无向图的邻接矩阵或邻接表存储并输出本题给出了一个无向图的邻接矩阵存储表示,在此基础上稍加改动就可以实现有向图、无向图和有向网的邻接矩阵表示。
实验2 建立图的邻接矩阵或邻接表存储并在此基础上实现图的深度优先遍历和广度优先遍历图的广度优先遍历用非递归方法很容易理解,非递归方法需要辅助队列Q以及出队、入队函数。
四、实验过程及结果分析源代码:#include<stdio.h>#include<malloc.h>#define MAX_NUM 20#define OK 1#define ERROR -1typedef int ElemType;typedef char VertexType;typedef struct ArcNode{ //定义弧结点ElemType data;ArcNode *nextarc;}ArcNode,*ArcLink;typedef struct VNode{ //定义顶点结点VertexType data;ArcLink firstarc;}VNode,AdjList[MAX_NUM];typedef struct{AdjList vdata;int vexnum,arcnum;}ALGraph;//构建图的邻接表int Creategraph(ALGraph &G,int n){ ArcLink p;int e,i;char v,w;for(i=0;i<n;i++){G.vdata[i].data='A'+i;G.vdata[i].firstarc=NULL;}printf("输入边的个数:\n");scanf("%d",&e);for(i=0;i<e;i++){getchar();//接收scanf的回车符printf("请输入某边所依附的两个顶点用A--%C表示\n",'A'+n-1); scanf("%c%c",&v,&w);//fflush(stdin);printf("V=%c,W=%c,I=%d\n",v,w,i);p=(ArcLink )malloc(sizeof(ArcNode));p->data=(int)(w-'A'+1);printf("%d\n",p->data);p->nextarc=G.vdata[(int)(v-'A')].firstarc;G.vdata[(int)(v-'A')].firstarc=p;p=(ArcLink)malloc(sizeof(ArcNode));p->data=(int)(v-'A'+1);p->nextarc=G.vdata[(int)(w-'A')].firstarc;G.vdata[(int)(w-'A')].firstarc=p;}G.vexnum=n; G.arcnum=e;return OK;}//输出邻接表int printGraph(ALGraph G){ArcLink p;int i;for(i=0;i<G.vexnum;i++){printf("%2d %c",i,G.vdata[i]);for(p=G.vdata[i].firstarc;p!=NULL;p=p->nextarc){ printf("-->");printf("%d",p->data);}printf("\n");}return OK;}int main(){ALGraph G;int n;printf("请输入你要构建的无向图的顶点个数:\n"); scanf("%d",&n);Creategraph(G,n);printf("你所构建的无向图的邻接表如下所示:\n"); printGraph(G);return OK;}1-1建立无向图的顶点数1-2建立无向图的边数1-3建立无向图五、成绩评定优良中及格不及格出勤内容格式创新效果总评指导教师:年月日。


洛谷邻接矩阵、邻接表的例题c++一、概述在学习和理解图的基本概念时,邻接矩阵和邻接表是两种常用的表示方法。
它们可以帮助我们更加直观地理解和分析图的结构和特性。
本文将以洛谷上的一个例题为例,介绍如何使用C++语言结合邻接矩阵和邻接表来解决图相关问题。
二、洛谷例题描述题目描述:给定一个有向图,图中包含n个节点和m条边,每条边连接两个节点。
现在需要求解图中每个节点的入度和出度。
输入格式:第一行包含两个整数n和m,分别表示节点数和边数。
接下来m行,每行包含两个整数a和b,表示图中存在一条边从a指向b。
输出格式:按照节点编号从小到大的顺序,输出每个节点的入度和出度。
三、解题思路1. 使用邻接矩阵表示图的结构;2. 使用邻接表统计每个节点的入度和出度。
四、基于邻接矩阵和邻接表的C++程序实现```cpp#include <iostream>#include <vector>using namespace std;const int MAXN = 1005;int n, m;int g[MAXN][MAXN]; // 邻接矩阵vector<int> inDegree(MAXN, 0); // 入度vector<int> outDegree(MAXN, 0); // 出度int m本人n() {cin >> n >> m;// 初始化邻接矩阵for (int i = 0; i < m; i++) {int a, b;cin >> a >> b;g[a][b] = 1;}// 统计入度和出度for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (g[i][j] == 1) { // 有一条边从i指向joutDegree[i]++;inDegree[j]++;}}}// 输出结果for (int i = 1; i <= n; i++) {cout << "节点" << i << "的入度为:" << inDegree[i] << ",出度为:" << outDegree[i] << endl;}return 0;}```五、测试样例输入样例:```5 61 21 32 32 43 44 5```输出样例:```节点1的入度为:0,出度为:2节点2的入度为:1,出度为:2节点3的入度为:2,出度为:2节点4的入度为:2,出度为:1节点5的入度为:1,出度为:0```六、总结通过本文的讲解,我们了解了如何使用C++语言结合邻接矩阵和邻接表来解决有关图的问题。

一、实验目的1. 理解邻接矩阵的概念及其在图论中的应用。
2. 掌握邻接矩阵的构建方法。
3. 学会使用邻接矩阵进行图的深度优先遍历和广度优先遍历。
4. 比较邻接矩阵和邻接表两种图的存储结构的优缺点。
二、实验内容1. 构建邻接矩阵2. 使用邻接矩阵进行图的深度优先遍历3. 使用邻接矩阵进行图的广度优先遍历4. 分析邻接矩阵和邻接表的优缺点三、实验环境1. 操作系统:Windows 102. 编程语言:C++3. 开发工具:Visual Studio 2019四、实验步骤1. 构建邻接矩阵(1)定义图的顶点数量n。
(2)创建一个nn的二维数组A,用于存储邻接矩阵。
(3)根据图的边信息,将对应的A[i][j]值设置为1(表示存在边)或0(表示不存在边)。
2. 使用邻接矩阵进行图的深度优先遍历(1)初始化访问标记数组visited,用于记录顶点是否被访问过。
(2)从某个顶点v开始,将其标记为已访问,并将其加入访问序列。
(3)对于v的每个邻接顶点u,如果u未被访问过,则递归调用深度优先遍历算法,并将u加入访问序列。
(4)重复步骤3,直到所有顶点都被访问过。
3. 使用邻接矩阵进行图的广度优先遍历(1)初始化队列Q和一个访问标记数组visited。
(2)将起始顶点v入队,并将其标记为已访问。
(3)当队列不为空时,执行以下步骤:a. 从队列中取出一个顶点v。
b. 将v的邻接顶点u入队,并将u标记为已访问。
c. 将v加入访问序列。
(4)重复步骤3,直到队列空为止。
4. 分析邻接矩阵和邻接表的优缺点(1)邻接矩阵的优点:a. 查找边的时间复杂度为O(1)。
b. 遍历图的时间复杂度为O(n^2)。
c. 适用于稠密图。
(2)邻接矩阵的缺点:a. 空间复杂度为O(n^2),对于稀疏图,空间利用率低。
b. 查找边和遍历图的时间复杂度较高。
(3)邻接表的优点:a. 空间复杂度为O(n+e),对于稀疏图,空间利用率高。
b. 查找边和遍历图的时间复杂度为O(n+e)。
一、实验目的、意义(1)熟悉图的邻接矩阵的表示方法;(2)掌握建立图的邻接矩阵算法;(3)加深对图的理解,逐步培养解决实际问题的编程能力二、实验内容及要求求有向网络中单源点到其它各个顶点v的最短路径。
具体要求:(1)建立图的邻接矩阵;(2)求有向网中单源点到其它各个顶点v的最短路径P[v]及带权长度D[v]。
三、实验所涉及的知识点1.图的邻接矩阵的表示方法;2.建立图的邻接矩阵算法;3.有向网中求最短路径算法和带权长度。
四、实验记录(调试过程及调试中遇到的问题及解决办法,其他算法的存在与实践等。
) 实验中对最短路径和求带权长度的算法不是很理解,这部分程序的编写对我来说难度也比较大。
通过上网查找资料,把程序调了出来。
五、实验结果及分析(所输入的数据及相应的运行结果,运行结果要有提示信息,运行结果采用截图方式给出。
)六、总结与体会(调试程序的心得与体会,若实验课上未完成调试,要认真找出错误并分析原因等。
)七、程序清单(包含注释)#include<string.h>#include<ctype.h>#include<malloc.h>#include<limits.h>#include<stdio.h>#include<stdlib.h>#include<math.h>#define TRUE 1#define FALSE 0#define OK 1#define MAX_NAME 5 //顶点字符串的最大长度+1#define MAX_INFO 20 //相关信息字符串的最大长度+1#define MAX_VERTEX_NUM 20//最大顶点数#define INFINITY INT_MAX //用整形最大值代替无穷typedef int VRType;typedef char InfoType;typedef char VertexType[MAX_NAME];typedef char InfoType;typedef int Status;typedef int Boolean;typedef int PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef int ShortPathTable[MAX_VERTEX_NUM];typedef enum{DG,DN,AG,AN}GraphKind;typedef struct{VRType adj; //顶点关系类型,无权图,用1/0表示相邻否,对于带权图,则为权值类型。
浅谈图论中邻接矩阵的应用[摘要] 使用邻接矩阵求解有关实际问题符合数学中数形结合的思想,对于更好地理解问题,思考问题从而求解问题具有现实意义。
图论知识的应用是相当广泛的,它是数学的重要分支,使今年来较为活跃的数学分支。
这个问题其实也是一个数学游戏问题,是源于生活,高于生活。
图论作为组合数学的一分支,与其他数学分支,如矩阵论,概率论,拓扑学数值分析都有着重要的联系。
[关键字] 邻接矩阵、算法、连通性、最小生成树1、引言首先介绍图论中邻接矩阵的一个重要定理:G是一个图,V (G)为G的顶点集, E(G)为G的边集。
设G中有n个顶点,v1,v2,…,vn;A=(aij)n ×n为G的邻接距阵, 其中定理1:设A (G)为图G的邻接距阵,则G中从顶点vi 到顶点vj,长度为k的道路的Ak条数为中的i行j列元素。
证:对k用数学归纳法k =1时,显然结论成立;假设k时,定理Al.A= Al+1成立,考虑k +1的情形。
记Al的i行j列元素为l≥2,因为所以(1)而从vi,vj到长k +1的道路无非是从vi 经k步到某顶点vl(1≤l≤n),再从vl走一步到vj; 由归纳假设从vl到vj长为k的道路共计而从vl到vj 长为1的道路为aij条,所以长为k+1的vl经过k部到vi再一步到vj的道路共有条故从vi经k +1步到vj的路径共有1、邻接矩阵现实问题中的运用锁具装箱问题某厂生产一种弹子锁具,每个锁具的钥匙有5个槽,每个槽的高度从{1, 2, 3, 4, 5, 6}6个数(单位略)中任取一数由于工艺及其他原因,制造锁具时对5个槽的高度还有两个限制:至少有3个不同的数,相邻两槽的高度之差不能为5,满足以上条件制造出来的所有互不相同的锁具称为一批。
销售部门在一批锁具中随意地取每60个装一箱出售。
问每一批具有多少个,装多少箱。
分析:锁具装箱这个问题是一个排列组合的数学问题,但在这里我们用图论中的邻接矩阵方法来解决这个问题。
离散数学实验3报告讲解实验报告⽬录第⼀章实验概述 (3)1.1实验⽬的 (3)1.2实验内容 (3)1.3实验环境 (3)第⼆章实验原理和实现过程 (4)2.1实验原理 (4)2.1.1建⽴图的邻接矩阵,判断图是否连通 (4)2.1.2 计算任意两个结点间的距离 (4)2.1.3对不连通的图输出其各个连通⽀ (5)2.2实验过程(算法描述) (5)2.2.1 程序整体思路 (5)2.2.2具体算法流程 (5)第三章实验数据及结果分析 (7)3.1建⽴图的邻接矩阵并判断图是否连通的功能测试及结果分析 (7)3.1.1输⼊⽆向图的边 (7)3.1.2建⽴图的连接矩阵 (8)3.2其他功能的功能测试和结果分析 (9)3.2.1计算节点间的距离 (9)3.2.2判断图的连通性 (9)3.2.3输出图的连通⽀ (10)3.2.4退出系统 (10)第四章实验收获和⼼得体会 (11)4.1实验收获 (11)4.2⼼得体会 (12)第五章实验源程序清单 (13)5.1程序代码 (13)第⼀章实验概述1.1 实验⽬的理解图论的基本概念,图的矩阵表⽰,图的连通性,图的遍历,以及求图的连通⽀⽅法。
通过实验,帮助学⽣更好地掌握计算机科学技术常⽤的离散数学中的概念、性质和运算,培养逻辑思维;通过实验提⾼学⽣编写实验报告、总结实验结果的能⼒,提⾼理论联系实际的能⼒;使学⽣具备程序设计的思想,能够独⽴完成简单的算法设计和分析。
1.2 实验内容以偶对的形式输⼊⼀个⽆向简单图的边,建⽴该图的邻接矩阵,判断图是否连通(A),并计算任意两个结点间的距离(B),对不连通的图输出其各个连通⽀(C)。
注意:题⽬类型分为A,B,C三类,其中A为基本题,完成A类题⽬可达到设计的基本要求,其他均为加分题,并按字母顺序分数增加越⾼。
基本要求如下:程序需具有基本的容错控制,在输⼊错误时有处理⼿段;程序界⾯友好,需要输⼊的地⽅有输⼊说明,说明输⼊的内容和格式要求等;实验原理和实现过程应该详细分析问题,给出解决思路,描述算法思想,不能⽤源程序代替算法;测试数据应全⾯,包括⾮法输⼊的处理结果等都应包含在内。
实验报告六图及图的操作实验一、实验目的:1、掌握图的基本概念和术语2、掌握图的存储结构及创建算法。
3、掌握图的遍历算法(递归或非递归算法)。
二、实验内容:1、图邻接矩阵存储结构表示及基本操作算法实现(1)邻接矩阵存储结构类定义:自定义如下:public interface LList<T> {boolean isEmpty();int length();T get(int i);void set(int i,T x);void insert(int i,T x);void append(T x);T remove(int i);void removeAll();}public class SeqList<T> implements LList<T> {private Object[] element;private int len;public SeqList(int size){this.element=new Object[size];this.len = 0;}public SeqList(SeqList<T> list){this(list.len);this.len=list.len;}public SeqList(){this(64);}public boolean isEmpty(){return this.len==0;}public int length(){return this.len;}public T get(int i){if(i>=0&&i<this.len)return (T)this.element[i];return null;}public void set(int i, T x){if(x==null)return;if(i>=0&&i<this.len)this.element[i] = x;elsethrow new IndexOutOfBoundsException(i+""); }public String toString(){String str = "(";if(this.len>0)str += this.element[0].toString();for(int i=1;i<this.len;i++)str +=","+this.element[i].toString();return str+")";}public void insert(int i, T x){if(x==null)return;if(this.len==element.length){Object[] temp = this.element;this.element=new Object[temp.length*2];for(int j=0;j < temp.length;i++)this.element[j]=temp[j];}if(i<0)i=0;if(i>this.len)i=this.len;for(int j=this.len-1;j>=i;j--)this.element[j+1] = this.element[j];this.element[i]=x;this.len++;}public void append(T x){insert(this.len,x);}public T remove(int i){if(this.len==0||i<0||i>=len)return null;T old = (T)this.element[i];for(int j=0;j<this.len-1;j++)this.element[j] = this.element[j+1];this.element[this.len-1]=null;this.len--;return old;}public void removeAll(){this.len=0;}}(2)创建邻接矩阵算法创建无向图邻接矩阵算法:public class MatrixGraph<T> {protected SeqList<T> vertexlist;protected int[][] adjmatrix;private final int Max=0;public MatrixGraph(int size){size=size<10?10:size;this.vertexlist=new SeqList<T>(size);this.adjmatrix=new int[size][size];for(int i=0;i<size;i++)for(int j=0;j<size;j++)this.adjmatrix[i][j]=(i==j)?0:Max;}public MatrixGraph(T[] vertices,Edge[] edges){ this(vertices.length);if(vertices==null)return;for(int i=0;i<vertices.length;i++)insertVertex(vertices[i]);if(edges!=null)for(int j=0;j<edges.length;j++)insertEdge(edges[j]);}public int vertexCount(){return this.vertexlist.length();}public T get(int i){return this.vertexlist.get(i);}public int getWeight(int i,int j){return this.adjmatrix[i][j];}public String toString(){String str="顶点集合:"+this.vertexlist.toString()+"\n 邻接矩阵:\n";int n=this.vertexCount();for(int i=0;i<n;i++){for(int j=0;j<n;j++)str+=this.adjmatrix[i][j]==Max?" 0":" "+this.adjmatrix[i][j];str+="\n";}return str;}public int insertVertex(T x){this.vertexlist.append(x);if(this.vertexCount()>this.adjmatrix.length){int temp[][]=adjmatrix,i,j;this.adjmatrix=new int[temp.length*2][temp.length^2];for(i=0;i<temp.length;i++){for(j=0;j<temp.length;j++)this.adjmatrix[i][j]=temp[i][j];for(j=temp.length;j<temp.length*2;i++)this.adjmatrix[i][j]=Max;}for(i=temp.length;i<temp.length*2;i++)for(j=0;j<temp.length*2;j++)this.adjmatrix[i][j]=(i==j)?0:Max;}return this.vertexlist.length()-1;}public void insertEdge(int i,int j,int weight){int n=this.vertexCount();if(i>=0&&i<n&&j>=0&&i!=j&&this.adjmatrix[i][j]==Max) this.adjmatrix[i][j]=weight;}public void insertEdge(Edge edge){this.insertEdge(edge.start,edge.dest,edge.weight);}}创建无向网邻接矩阵算法:public class MatrixGraph<T> {protected SeqList<T> vertexlist;protected int[][] adjmatrix;private final int Max=99999;public MatrixGraph(int size){size=size<10?10:size;this.vertexlist=new SeqList<T>(size);this.adjmatrix=new int[size][size];for(int i=0;i<size;i++)for(int j=0;j<size;j++)this.adjmatrix[i][j]=(i==j)?0:Max;}public MatrixGraph(T[] vertices,Edge[] edges){this(vertices.length);if(vertices==null)return;for(int i=0;i<vertices.length;i++)insertVertex(vertices[i]);if(edges!=null)for(int j=0;j<edges.length;j++)insertEdge(edges[j]);}public int vertexCount(){return this.vertexlist.length();public T get(int i){return this.vertexlist.get(i);}public int getWeight(int i,int j){return this.adjmatrix[i][j];}public String toString(){String str="顶点集合:"+this.vertexlist.toString()+"\n 邻接矩阵:\n";int n=this.vertexCount();for(int i=0;i<n;i++){for(int j=0;j<n;j++)str+=this.adjmatrix[i][j]==Max?" ∞":" "+this.adjmatrix[i][j];str+="\n";}return str;}public int insertVertex(T x){this.vertexlist.append(x);if(this.vertexCount()>this.adjmatrix.length){int temp[][]=adjmatrix,i,j;this.adjmatrix=new int[temp.length*2][temp.length^2];for(i=0;i<temp.length;i++){for(j=0;j<temp.length;j++)this.adjmatrix[i][j]=temp[i][j];for(j=temp.length;j<temp.length*2;i++)this.adjmatrix[i][j]=Max;}for(i=temp.length;i<temp.length*2;i++)for(j=0;j<temp.length*2;j++)this.adjmatrix[i][j]=(i==j)?0:Max;}return this.vertexlist.length()-1;}public void insertEdge(int i,int j,int weight){int n=this.vertexCount();if(i>=0&&i<n&&j>=0&&i!=j&&this.adjmatrix[i][j]==Max)this.adjmatrix[i][j]=weight;}public void insertEdge(Edge edge){this.insertEdge(edge.start,edge.dest,edge.weight);}}创建有向图邻接矩阵算法:(可使用前无向图邻接矩阵算法)创建有向网邻接矩阵算法:(可使用前无向图邻接矩阵算法)(3)输出邻接矩阵结果算法public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,1),new Edge(0,3,1),new Edge(1,0,1),new Edge(1,2,1),new Edge(1,3,1),new Edge(2,1,1),new Edge(2,3,1),new Edge(2,4,1),new Edge(3,0,1),new Edge(3,1,1),new Edge(3,2,1),new Edge(3,4,1),new Edge(4,2,1),new Edge(4,3,1),};MatrixGraph<String> graph=new MatrixGraph<String>(vertices,edges);System.out.println("无向图:"+graph.toString());}public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,5),new Edge(0,3,2),new Edge(1,0,5),new Edge(1,2,7),new Edge(1,3,6),new Edge(2,1,7),new Edge(2,3,8),new Edge(2,4,3),new Edge(3,0,2),new Edge(3,1,6),new Edge(3,2,8),new Edge(3,4,9),new Edge(4,2,3),new Edge(4,3,9)};MatrixGraph<String> graph=new MatrixGraph<String>(vertices,edges);System.out.println("无向网:"+graph.toString());}public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,1),new Edge(0,3,1),new Edge(1,3,1),new Edge(2,3,1),new Edge(2,4,1),new Edge(3,1,1),new Edge(3,2,1),new Edge(4,2,1),new Edge(4,3,1)};MatrixGraph<String> graph=new MatrixGraph<String>(vertices,edges);System.out.println("有向图:"+graph.toString());}public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,5),new Edge(0,3,2),new Edge(1,3,6),new Edge(2,3,8),new Edge(2,4,3),new Edge(3,1,9),new Edge(3,2,2),new Edge(4,2,3),new Edge(4,3,9)};MatrixGraph<String> graph=new MatrixGraph<String>(vertices,edges);System.out.println("有向网:"+graph.toString());}测试结果粘贴如下:2、图邻接表存储结构表示及基本操作算法实现(1)邻接表存储结构类定义:自定义如下:public class Vertex<T> {public T data;public SortedSinglyLinkedList<Edge> adjlink;public Vertex(T data){this.data=data;this.adjlink=new SortedSinglyLinkedList<Edge>();}public String toString(){return"\n"+this.data.toString()+": "+this.adjlink.toString();}}(2)创建邻接表算法创建无向网邻接表算法:(可使用下有向网邻接表算法)创建有向网邻接表算法:public class AdjListGraph<T> {protected SeqList<Vertex<T>> vertexlist;public AdjListGraph(int size){size=size<10?10:size;this.vertexlist=new SeqList<Vertex<T>>(size);}public AdjListGraph(T[] vertices,Edge[] edges){this(vertices.length*2);if(vertices==null)return;for(int i=0;i<vertices.length;i++)insertVertex(vertices[i]);if(edges!=null)for(int j=0;j<edges.length;j++)insertEdge(edges[j]);}public String toString(){return"出边表: \n"+this.vertexlist.toString()+"\n";}public int insertVertex(T x){this.vertexlist.append(new Vertex<T>(x));return this.vertexlist.length()-1;}public int vertexCount(){return this.vertexlist.length();}public void insertEdge(int i,int j,int weight){if(i>=0&&i<vertexCount()&&j>=0&&j<vertexCount()&&i!=j){Edge edge=new Edge(i,j,weight);SortedSinglyLinkedList<Edge>adjlink=this.vertexlist.get(i).adjlink;Node<Edge> front=adjlink.head,p=front.next;while(p!=null&&pareTo(edge)<0){front=p;p=p.next;}if(p!=null&&pareTo(edge)==0)return;front.next=new Node<Edge>(edge,p);}}public void insertEdge(Edge edge){this.insertEdge(edge.start,edge.dest,edge.weight);}(3)输出邻接表结果算法public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,5),new Edge(0,3,2),new Edge(1,0,5),new Edge(3,0,2),new Edge(2,4,3),new Edge(4,2,3)};AdjListGraph<String> graph=new AdjListGraph<String>(vertices,edges);System.out.println("无向网:"+graph.toString());}public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,5),new Edge(0,3,2),new Edge(1,0,6),new Edge(1,2,7),new Edge(2,4,3),new Edge(3,2,8),new Edge(3,4,9)};AdjListGraph<String> graph=new AdjListGraph<String>(vertices,edges);System.out.println("有向网:"+graph.toString());}测试结果粘贴如下:3、图的遍历递归算法(1)(存储结构为邻接表)深度优先遍历算法递归算法:public interface QQueue<T> {boolean isEmply();void enqueue(T x);T dequeue();}public class SeqQueue<T> implements QQueue<T>{private Object element[];private int front,rear;public SeqQueue(int length){if(length<64)length=64;this.element=new Object[Math.abs(length)];this.front=this.rear=0;}public SeqQueue(){this(64);}public boolean isEmply(){return this.front==this.rear;}public void enqueue(T x){if(x==null)return;if(this.front==(this.rear+1)%this.element.length){ Object[] temp = this.element;this.element=new Object[temp.length*2];int i=this.front,j=0;while(i!=this.rear){this.element[j]=temp[i];i=(i+1)%temp.length;j++;}this.front=0;this.rear=j;}this.element[this.rear]=x;this.rear=(this.rear+1)%this.element.length;}public T dequeue(){if(isEmply())return null;T temp=(T)this.element[this.front];this.front=(this.front+1)%this.element.length;return temp;}public String toString(){String str="(";if(!isEmply()){str+=this.element[this.front].toString();int i=(this.front+1)%this.element.length;while(i!=this.rear){str+=","+this.element[i].toString();i=(i+1)%this.element.length;}}return str+=")";}public int length(){return(this.element.length+this.rear-this.front)%(this.element.length);}}public abstract class AbstractGraph<T> {public abstract int vertexCount();public abstract T get(int i);public abstract int getNextNeighbor(int i,int j);public void DFSTraverse(int i){boolean[] visited= new boolean[this.vertexCount()];int j=i;do{if(!visited[j]){System.out.print("{");this.depthfs(j,visited);System.out.print("}");}j=(j+1)%this.vertexCount();}while(j!=i);System.out.println();}public void depthfs(int i,boolean[] visited){System.out.print(this.get(i)+" ");visited[i]=true;int j=this.getNextNeighbor(i, -1);while(j!=-1){if(!visited[j])depthfs(j,visited);j=this.getNextNeighbor(i, j);}}}public class AdjListGraph<T> extends AbstractGraph<T>{ protected SeqList<Vertex<T>> vertexlist;public AdjListGraph(int size){size=size<10?10:size;this.vertexlist=new SeqList<Vertex<T>>(size);}public T get(int i){return this.vertexlist.get(i).data;}public AdjListGraph(T[] vertices,Edge[] edges){this(vertices.length*2);if(vertices==null)return;for(int i=0;i<vertices.length;i++)insertVertex(vertices[i]);if(edges!=null)for(int j=0;j<edges.length;j++)insertEdge(edges[j]);}public String toString(){return"出边表: \n"+this.vertexlist.toString()+"\n";}public int insertVertex(T x){this.vertexlist.append(new Vertex<T>(x));return this.vertexlist.length()-1;}public int vertexCount(){return this.vertexlist.length();}public void insertEdge(int i,int j,int weight){if(i>=0&&i<vertexCount()&&j>=0&&j<vertexCount()&&i!=j){ Edge edge=new Edge(i,j,weight);SortedSinglyLinkedList<Edge>adjlink=this.vertexlist.get(i).adjlink;Node<Edge> front=adjlink.head,p=front.next;while(p!=null&&pareTo(edge)<0){front=p;p=p.next;}if(p!=null&&pareTo(edge)==0)return;front.next=new Node<Edge>(edge,p);}}public void insertEdge(Edge edge){this.insertEdge(edge.start,edge.dest,edge.weight);}public int getNextNeighbor(int i,int j){int n=this.vertexCount();if(i>=0&&i<n&&j>=-1&&j<n&&i!=j){Node<Edge> p=this.vertexlist.get(i).adjlink.head.next;while(p!=null){if(p.data.dest>j)return p.data.dest;p=p.next;}}return -1;}public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,1),new Edge(0,3,1),new Edge(1,0,1),new Edge(1,2,1),new Edge(1,3,1),new Edge(3,0,1),new Edge(3,1,1),new Edge(3,2,1),newEdge(3,4,1),new Edge(2,3,1),new Edge(2,1,1),new Edge(2,4,1),new Edge(4,2,1),new Edge(4,3,1)};AdjListGraph<String> graph=new AdjListGraph<String>(vertices,edges);System.out.println(graph.toString());for(int i=0;i<graph.vertexCount();i++){graph.DFSTraverse(i);}}}public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,1),new Edge(0,3,1),new Edge(1,0,1),new Edge(1,2,1),new Edge(3,2,1),new Edge(3,4,1),new Edge(2,4,1),};AdjListGraph<String> graph=new AdjListGraph<String>(vertices,edges);System.out.println(graph.toString());for(int i=0;i<graph.vertexCount();i++){graph.DFSTraverse(i);}}测试结果粘贴如下:有向网的测试结果:无向网的测试结果:(2)广度优先遍历算法非递归算法public abstract class AbstractGraph<T> {public abstract int vertexCount();public abstract T get(int i);public abstract int getNextNeighbor(int i,int j);public void BFSTraverse(int i){boolean[] visited=new boolean[this.vertexCount()];int j=i;do{if(!visited[j]){System.out.print("{");breadthfs(j,visited);System.out.print("}");}j=(j+1)%this.vertexCount();}while(j!=i);System.out.println();}public void breadthfs(int i,boolean[] visited){System.out.print(this.get(i)+" ");visited[i]=true;SeqQueue<Integer> que=new SeqQueue<Integer>(this.vertexCount());que.enqueue(new Integer(i));while(!que.isEmply()){i=que.dequeue().intValue();int j=this.getNextNeighbor(i, -1);while(j!=-1){if(!visited[j]){System.out.print(this.get(j)+"");visited[j]=true;que.enqueue(new Integer(j));}j=this.getNextNeighbor(i, j);}}}}public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,1),new Edge(0,3,1),new Edge(1,0,1),new Edge(1,2,1),new Edge(3,2,1),new Edge(3,4,1),new Edge(2,4,1),};AdjListGraph<String> graph=new AdjListGraph<String>(vertices,edges);System.out.println(graph.toString());for(int i=0;i<graph.vertexCount();i++){graph.BFSTraverse(i);}}public static void main(String[] args){String[] vertices={"A","B","C","D","E"};Edge edges[]={new Edge(0,1,1),new Edge(0,3,1),new Edge(1,0,1),new Edge(1,2,1),new Edge(1,3,1),new Edge(3,0,1),new Edge(3,1,1),new Edge(3,2,1),newEdge(3,4,1),new Edge(2,3,1),new Edge(2,1,1),new Edge(2,4,1),new Edge(4,2,1),new Edge(4,3,1)};AdjListGraph<String> graph=new AdjListGraph<String>(vertices,edges);System.out.println(graph.toString());for(int i=0;i<graph.vertexCount();i++){graph.BFSTraverse(i);}}测试结果粘贴如下:有向网的测试结果:无向网的测试结果:三、实验心得(含上机中所遇问题的解决办法,所使用到的编程技巧、创新点及编程的心得)图这一章牵涉很广,仅是上三道题,就需要线性表、单链表、队列三种存储方式。
图的存储实验报告图的存储实验报告引言在计算机科学领域中,图是一种重要的数据结构,用于描述对象之间的关系。
图的存储方式对于图的遍历、搜索和其他操作有着重要的影响。
本实验旨在探究不同的图存储方式,并比较它们在不同操作下的性能差异。
一、邻接矩阵存储方式邻接矩阵是一种常见的图存储方式,它使用二维数组来表示图中各个顶点之间的关系。
在邻接矩阵中,行和列分别代表图中的顶点,矩阵中的元素表示两个顶点之间的边的关系。
实验中,我们通过一个简单的例子来说明邻接矩阵的存储方式。
假设有一个无向图,其中包含5个顶点和6条边。
我们可以使用一个5x5的矩阵来表示这个图,矩阵中的元素为1表示两个顶点之间存在边,为0表示不存在边。
邻接矩阵的优点是可以快速判断两个顶点之间是否存在边,时间复杂度为O(1)。
然而,邻接矩阵的缺点是当图中的边数较少时,会造成存储空间的浪费。
此外,在图中顶点的增加和删除操作时,需要重新调整矩阵的大小,开销较大。
二、邻接表存储方式邻接表是另一种常见的图存储方式,它使用链表来表示图中各个顶点之间的关系。
在邻接表中,每个顶点都有一个链表,链表中存储了与该顶点相邻的顶点。
实验中,我们同样以一个简单的例子来说明邻接表的存储方式。
假设有一个有向图,其中包含4个顶点和5条边。
我们可以使用一个包含4个链表的数组来表示这个图,数组中的每个元素表示一个顶点,链表中的元素表示与该顶点相邻的顶点。
邻接表的优点是在图中边的数量较少时,可以节省存储空间。
此外,在图中顶点的增加和删除操作时,开销较小。
然而,邻接表的缺点是判断两个顶点之间是否存在边的时间复杂度较高,需要遍历链表,时间复杂度为O(顶点的度数)。
三、性能比较与结论通过实验,我们对比了邻接矩阵和邻接表两种图存储方式在不同操作下的性能差异。
在判断两个顶点之间是否存在边的操作中,邻接矩阵的时间复杂度为O(1),而邻接表的时间复杂度为O(顶点的度数)。
因此,在此操作下,邻接矩阵的性能更优。
邻接矩阵的生成
一、实验目的
了解邻接矩阵的定义和其基本概念以及构建方式。
二、实验内容
1、根据已知图形的内容输入相关参数生成邻接矩阵;
2、用C语言编程来实现此算法。
用下面的实例来调试程序:
三、使用环境
Xcode编译器,编写语言C。
四、编程思路
邻接矩阵表示的是顶点与边的关系,因此需要一个一维数组Vertex[]来保存顶点的相关信息,一个二维数组Edges[][]来保存边的权植,因为C语言二维数组的输出需要用循环语句,因此为了方便,构造一个输出函数Out,用来打印数组各元素的数值。
五、调试过程
1.程序代码:
#include <stdio.h>
#define VERTEX_MAX 26//最大顶点数目
#define MAXVALUE 32767//顶点最大权值
//定义图
typedef struct
{
char Vertex[VERTEX_MAX]; //保存顶点信息
int Edges[VERTEX_MAX][VERTEX_MAX]; //保存边的权值
int isTrav[VERTEX_MAX]; //是否遍历
int VertexNum ; //顶点数目
int EdgeNum; //边的数目
}Graph;
//创建邻接矩阵
void Create(Graph *G)
{
int i,j,k,weight; //i,j,k分别为迭代数,weight是权值
char start,end; //边或者弧的起始顶点
printf("输入各个顶点的信息:\n"); //输入各个顶点的信息
for(i=0;i<G->VertexNum;i++)
{
getchar();
printf("这是第%d 个顶点的名字:",i+1);
scanf("%c",&(G->Vertex[i]));//保存到数组中
}
//输入每个边的起始顶点和权值
printf("输入每个边的起始顶点和权值,例如A,B,1:\n");
for(k=0;k<G->EdgeNum;k++)
{
getchar();
printf("这是第%d 个边:",k+1);
scanf("%c,%c,%d",&start,&end,&weight);//起点,终点,权值
for(i=0;start!=G->Vertex[i];i++);//查找起点
for(j=0;end!=G->Vertex[j];j++); //查找终点
G->Edges[i][j]=weight;//保存权值
G->Edges[j][i]=weight;
}
}
void Out(Graph *G) //输出邻接矩阵
{
int i,j;//迭代数
for(j=0;j<G->VertexNum;j++)
{
printf("\t%c",G->Vertex[j]);
} //第一行输出顶点信息
printf("\n");
for(i=0;i<G->VertexNum;i++)
{
printf("%c",G->Vertex[i]);
for(j=0;j<G->VertexNum;j++)
{
if(G->Edges[i][j]==MAXVALUE) //如果权是最大值就输出MAX printf("\tMAX");
else
printf("\t%d",G->Edges[i][j]);//否则就输出权值
}
printf("\n");
}
}
int main()
{
Graph G;
int i,j;//迭代数
//输入顶点数目和边的数目
printf("输入顶点数目和边的数目,例如1,2:");
scanf("%d,%d",&G.VertexNum,&G.EdgeNum);//保存顶点和边的数目
for(i=0;i<G.VertexNum;i++)//清空矩阵
for(j=0;j<G.VertexNum;j++)
G.Edges[i][j]=MAXVALUE;//设置各元素的值为最大值
Create(&G);//创建邻接矩阵
printf("邻接矩阵为:\n");
Out(&G);//输出邻接矩阵
getchar();
return0;
}
2.运行窗口:
在运行窗口输入:输出为:
则输出:
所以连通分支如下:。