人教版中考数学二轮复习专题练习上二次函数与分割面积

人教版中考数学专题复习二次函数综合题1．已知二次函数2(0)y ax bx a =+≠，其对称轴为直线x=t ．（1）当a=1，b=4时，t=________；（2）当a<0时，若点A(1，m)，B(5，n)在此二次函数图象上，且m<n ，则t 的取值范围是________；（3）已知点C(0，a)，D(2，3a -2b)，若此二次函数图象与线段CD 有且仅有一个公共点，求t 的取值范围．2．如图，已知顶点是M 的抛物线()230y ax bx a =+-≠与x 轴交于()1,0A -，()3,0B 两点，与y 轴交于点C ．（1）求抛物线对应的函数解析式；（2）点P 是x 轴上方抛物线上的一点，若PAB △的面积等于3，求点P 的坐标．（3）是否在y 轴存在一点Q ，使得QBM 为直角三角形？若存在，求出Q 的坐标，若不存在，说明理由．3．如图，抛物线y ＝（x ﹣1）2﹣4的图象与x 轴交于的A 、B 两点，与y 轴交于点D ，抛物线的顶点为C ．（1）求△ABD 的面积；（2）求△ABC 的面积；（3）点P 是抛物线上一动点，当△ABP 的面积为4时，求所有符合条件的点P 的坐标；（4）点P 是抛物线上一动点，当△ABP 的面积为8时，求所有符合条件的点P 的坐标；（5）点P 是抛物线上一动点，当△ABP 的面积为10时，求所有符合条件的点P 的坐标．4．如图，已知抛物线经过点(1,0)A -，(3,0)B ，(0,3)C 三点．（1）求抛物线的解析式；（2）点M 是线段BC 上的点（不与B ，C 重合），过M 作//MN y 轴交抛物线于N 点，若点M 的横坐标为m ，请用含m 的代数式表示MN 的长；（3）在（2）的条件下，连接NB ，NC ，当m 为何值时，BNC 的面积最大．5．如图，在平面直角坐标系中，抛物线2y x bx c =-++，与y 轴交于点A 与x 轴交于点E 、B ．且点()0,5A ，()5,0B ，点P 为抛物线上的一动点．（1）求二次函数的解析式；（2）如图1，过点A 作AC 平行于x 轴，交抛物线于点C ，若点P 在AC 的上方，作PD 平行于y 轴交AB 于点D ，连接PA ，PC ，当245AOE APCD S S ∆=四边形时，求点P 坐标； （3）设抛物线的对称轴与AB 交于点M ，点Q 在直线AB 上，当以点M 、E 、P 、Q 为顶点的四边形为平行四边形时，请直接写出点Q 的坐标．6．如图是二次函数y ＝（x+2）2的图象，顶点为A ，与y 轴的交点为B ．（1）求经过A，B两点的直线的函数关系式；（2）请在第二象限中的抛物线上找一点C，使△ABC的面积与△ABO的面积相等；（3）已知抛物线上存在点P，使△PAB为等腰三角形，则所有符合条件的这样的点P共有几个?7．如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B，C三点，点A的坐标是(3，0)，点C的坐标是(0，﹣3)，动点P在抛物线上．（1）b= ，c= （直接填写结果）（2）是否存在点P，使得ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；8．已知，点A是平面直角坐标系内的一点，将点A绕坐标原点O逆时针旋转90°得到点B，经过A、O、B 三点的二次函数的图象记为G．（1）若点A的坐标为（1，2），求二次函数G的解析式；（2）若点A的坐标为（m，2m）（m≠0），图象G所对应的函数表达式为y=ax2+bx（a、b为常数，a≠0）．写出b 的值，并用含m 的代数式表示a ．（直接写出即可）（3）在（2）的条件下，直线x=-2与图象G 交于点P ，直线x=1与图象G 交于点Q ．图象G 在P 、Q 之间的部分（包含P 、Q 两点）记为G 1．①当图象G 在-2≤x≤1上的函数值y 随自变量x 的增大而增大时，设图象G 1的最高点的纵坐标为h 1，最低点的纵坐标为h 2，记h=h 1-h 2，求h 的取值范围．②连结PQ ，当PQ 与图象G 1围成的封闭图形与x 轴交于点D （点D 不与坐标原点重合）．当OD≥12时，直接写出m 的取值范围．9．如图，直线y ＝﹣12x ＋2交y 轴于点A ，交x 轴于点C ，抛物线y ＝﹣14x 2＋bx ＋c 经过点A ，点C ，且交x 轴于另一点B ．（1）点A 的坐标为 ，点C 的坐标为 ，并求抛物线的解析式；（2）在直线AC 上方的抛物线上有一点M ，求四边形ABCM 面积的最大值及此时点M 的坐标；（3）将线段OA 绕x 轴上的动点P （m ，0）顺时针旋转90°得到线段O A ''，若线段O A ''与抛物线只有一个公共点，请你直接写出m 的取值范围．10．如图，平面直角坐标系xoy 中，抛物线223y x x =--与x 轴交于点A ，B ，与y 轴交于点C ．（1）求顶点D 的坐标；（2）求ABC 的面积．11．如图，抛物线2(0)y ax bx c a =++≠与x 轴交于A ，B 两点，与y 轴交于点C ，抛物线的对称轴交x 轴于点D ，已知A （﹣2，0），B （4，0），C （0，8）．（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在点P ，使△PCD 是等腰三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）点E 是线段BC 上的一个动点，过点E 作x 轴的垂线与抛物线相交于点F ，求△CBF 的最大面积及此时点E 的坐标．12．如图1，在平面直角坐标系xOy 中，抛物线y ＝ax 2+bx+c 与x 轴分别相交于A 、B 两点，与y 轴相交于点C ，下表给出了这条抛物线上部分点（x ，y ）的坐标值：（2）如图1，直线1y kx =+()0k <与抛物线交于P ，Q 两点，交抛物线对称轴于点T ，若QMT 的面积是PMT 面积的两倍，求k 的值；（3）如图2，点D 是第四象限内抛物线上一动点，过点D 作DF⊥x 轴，垂足为F ，ABD 的外接圆与DF 相交于点E ．试问：线段EF 的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．13．如图，在平面直角坐标系中，二次函数y ＝x 2+bx+c 的图象与x 轴交于A 、B 两点，A 点在原点左侧，B 点的坐标为（4，0），与y 轴交于C （0，﹣4）点，点P 是直线BC 下方的抛物线上一动点．（1）求这个二次函数的表达式；（2）连接PO 、PC ，并把△POC 沿CO 翻折，得到四边形POP′C，那么是否存在点P ，使四边形POP′C 为菱形？若存在，请求出此时点P 的坐标；若不存在，请说明理由．14．如图，在平面直角坐标系xoy 中，抛物线21522y x bx =-++与x 轴交于点1,0A ，抛物线的对称轴l 经过顶点B ，作直线AB ．P 是该抛物线上一点，过点P 作x 轴的垂线交AB 于点Q ，过点P 作PNl 于点N ，以PQ 、P N 为边作矩形PQMN ．（1）b =______；（2）当点P 在抛物线A ，B 两点之间时，求线段PQ 长度的最大值；（3）矩形PQMN 与此抛物线相交，抛物线被截得的部分图象记作G ，G 的最高点的纵坐标为m ，最低点纵坐标为n ，当2m n -=时，求点P 的坐标．。

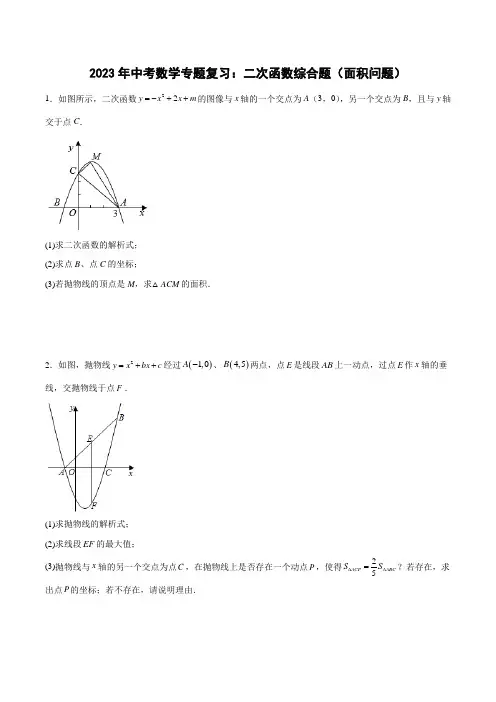
2023年中考数学专题复习：二次函数综合题（面积问题）1．如图所示，二次函数22y x x m =-++的图像与x 轴的一个交点为A （3，0），另一个交点为B ，且与y 轴交于点C ．(1)求二次函数的解析式；(2)求点B 、点C 的坐标；(3)若抛物线的顶点是M ，求△ACM 的面积．2．如图，抛物线2y x bx c =++经过()1,0A -、()4,5B 两点，点E 是线段AB 上一动点，过点E 作x 轴的垂线，交抛物线于点F ．(1)求抛物线的解析式；(2)求线段EF 的最大值；(3)抛物线与x 轴的另一个交点为点C ，在抛物线上是否存在一个动点P ，使得25ACP ABC S S ∆∆=？若存在，求出点P 的坐标；若不存在，请说明理由．3．如图，二次函数23y ax bx=++的图像与x正半轴相交于点B，负半轴相交于点A，其中A点坐标是（－1，0），B点坐标是（3，0）．(1)求此二次函数的解析式；(2)如图1，点P在第一象限的抛物线上运动，过点P作PD x⊥轴于点D，交线段BC于点E，线段BC把△CPD 分割成两个三角形的面积比为1∶2，求P点坐标；(3)如图2，若点H在抛物线上，点F在x轴上，当以B、C、H、F为顶点的四边形是平行四边形时，请直接写出点F的坐标．4．如图，已知直线y＝43x+4与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝﹣1．(1)求抛物线的表达式；(2)D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；(3)若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．5．如图，已知在平面直角坐标系xOy中，抛物线y=-12x2+bx+c经过点A（-2，0）．与点C（0，4）．与x轴的正半轴交于点B．(1)求抛物线的表达式；(2)如果D是抛物线上一点，AD与线段BC相交于点E，且AD将四边形ABDC分成面积相等的两部分，求DE AE的值；(3)如果P是x轴上一点，∠PCB=∠ACO，求∠PCO的正切值．6．如图，抛物线23y ax bx =+-交x 轴于()30A -,，()10B ,两点，与y 轴交于点.C 连接AC ，BC ．(1)求抛物线的解析式；(2)如图1，点P 为抛物线在第三象限的一个动点，PM x ⊥轴于点M ，交AC 于点G ，PE AC ⊥于点E ，当PGE 的面积为1时，求点P 的坐标；(3)如图2，若Q 为抛物线上一点，直线OQ 与线段AC 交于点N ，是否存在这样的点Q ，使得以A ，O ，N 为顶点的三角形与ABC 相似．若存在，请求出此时点Q 的坐标；若不存在，请说明理由．7．在平面直角坐标系中，已知抛物线经过A （－4，0），B （0，－4），C （2，0）三点．(1)求抛物线的解析式；(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．(3)若点P 是抛物线上的动点，点Q 是直线y ＝－x 上的动点，判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标．8．如图，二次函数23y ax bx =++的图象经过点A （-1，0），B （3，0），与y 轴交于点C ．(1)求二次函数的解析式；(2)第一象限内的二次函数23y ax bx =++图象上有一动点P ，x 轴正半轴上有一点D ，且OD =2，当S △PCD =3时，求出点P 的坐标；(3)若点M 在第一象限内二次函数图象上，是否存在以CD 为直角边的Rt MCD ，若存在，求出点M 的坐标，若不存在，请说明理由．9．如图，在平面直角坐标系中，已知抛物线y =ax 2+4x +c 与直线AB 相交于点A (0，1)和点B (3，4)．(1)求该抛物线的解析式；(2)设C 为直线AB 上方的抛物线上一点，连接AC ，BC ，以AC ，BC 为邻边作平行四边形ACBP ，求四边形ACBP 面积的最大值；(3)将该抛物线向左平移2个单位长度得到抛物线y =a 1x 2+b 1x +c 1（a 1≠0），平移后的抛物线与原抛物线相交于点D ，是否存在点E 使得△ADE 是以AD 为腰的等腰直角三角形？若存在，直接写出．．．．点E 的坐标；若不存在，请说明理由．10．如图，在平面直角坐标系中，抛物线2(0)y ax bx c a =++≠与x 轴交于A ，B 两点（A 在B 的左侧），与y 轴的交点为C ()0,3-，顶点为()1,4D -．(1)求抛物线的表达式；(2)若平行于x轴的直线与抛物线交于M，N两点，与抛物线的对称轴交于点H，若点H到x轴的距离是线，求线段MN的长；段MN长的12(3)若经过C，D两点的直线与x轴相交于点E，F是y轴上一点，且AF∥CD，在抛物线上是否存在点P，使直线PB恰好将四边形AECF的周长和面积同时平分？如果存在, 求出点P的坐标；如果不存在，请说明理．11．如图，已知抛物线y＝ax2+4x+c经过A（2，0）、B（0，﹣6）两点，其对称轴与x轴交于点C．(1)求该抛物线和直线BC的解析式；(2)设抛物线与直线BC相交于点D，求△ABD的面积；(3)在该抛物线的对称轴上是否存在点Q，使得△QAB的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．12．如图，抛物线y ＝ax 2+bx +c 与x 轴交于A （﹣2，0）、B （6，0）两点，与y 轴交于点 C ．直线l 与抛物线交于A 、D 两点，与y 轴交于点E ，点D 的坐标为（4，3）．(1)求抛物线的解析式与直线l 的解析式；(2)若点P 是抛物线上的点且在直线l 上方，连接P A 、PD ，求△P AD 面积最大值；(3)由（2）并求出点 P 的坐标．13．已知抛物线2y ax c =+过点()2,0A -和()1,3D -两点，交x 轴于另一点B ．(1)求抛物线解析式；(2)如图1，点P 是BD 上方抛物线上一点，连接AD ，BD ，PD ，当BD 平分ADP 时，求P 点坐标；(3)将抛物线图象绕原点O 顺时针旋转90°形成如图2的“心形”图案，其中点M ，N 分别是旋转前后抛物线的顶点，点E 、F 是旋转前后抛物线的交点．①直线EF 的解析式是______；②点G 、H 是“心形”图案上两点且关于EF 对称，则线段GH 的最大值是______．14．如图，抛物线2142y x x =-++与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ．(1)求A ，B ，C 三点的坐标，并直接写出直线AC 的函数表达式；(2)若D 是第一象限内抛物线上一动点，且△BCD 的面积等于△AOC 的面积，求点D 的坐标；(3)在（2）的条件下，连接AD ，试判断在抛物线上是否存在点M ，使∠MDA ＝∠ACO ？若存在，请直接写出点M 的坐标；若不存在，请说明理由．15．综合与探究如图，在平面直角坐标系中，直线y x b =+与x 轴交于点()4,0A ，与y 轴交于点B ，过A ，B 两点的抛物线交x 轴于另一点C ，且2OA OC =，点F 是直线AB 下方抛物线上的动点，连接F A ，FB ．(1)求抛物线解析式；(2)当点F 与抛物线的顶点重合时，ABF 的面积为______；．(3)求四边形F AOB 面积的最大值及此时点F 的坐标．(4)在（3）的条件下，点Q 为平面内y 轴右侧的一点，是否存在点Q 及平面内另一点M ，使得以A ，F ，Q ，M 为顶点的四边形是正方形？若存在，直接写出点Q 的坐标；若不存在，说明理由．16．抛物线224y ax ax =--交x 轴于(2,0)A -、B 两点，交y 轴于C ；直线AD 交抛物线于第一象限内点D ，且D 的横坐标为5，(1)求抛物线解析式；(2)点E 为直线AD 下方抛物线上一动点，且21ADE S =，求点E 的坐标；(3)抛物线上是否存在点P ，使PCO DAO CBO ∠+∠=∠，若存在，请求出此时点P 的坐标；若不存在，请说明理由．17．如图，在平面直角坐标系中，矩形OABC 的两边OA ，OC 分别在x 轴和y 轴上，3OA =，4OC =，抛物线24y ax bx =++经过点B ，且与x 轴交于点()1,0D -和点E ．(1)求抛物线的表达式：(2)若P 是第一象限抛物线上的一个动点，连接CP ，PE ，当四边形OCPE 的面积最大时，求点P 的坐标，此时四边形OCPE 的最大面积是多少；(3)若N 是抛物线对称轴上一点，在平面内是否存在一点M ，使以点C ，D ，M ，N 为顶点的四边形是矩形？若存在，请直接写出点M 的坐标；若不存在，说明理由．18．如图，抛物线与x 轴交于点()2,0B -、()4,0C 两点，与y 轴交于点()0,2A ；(1)求出此抛物线的解析式；(2)如图1，在直线AC 上方的抛物线上有一点M ，求AMC S △的最大值；(3)如图2，将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90°得到线段O A ''，若线段O A ''与抛物线只有一个公共点，请结合函数图象，求m 的取值范围；19．如图，已知抛物线2y x bx c =++与x 轴交于点A ，B （点A 在点B 的左侧），与y 轴交于点C ，OA =OC =3．(1)求抛物线的函数表达式；(2)若点P 为直线AC 下方抛物线上一点，连接BP 并交AC 于点Q ，若AC 分ABP △的面积为1：2两部分，请求出点P 的坐标；(3)在y 轴上是否存在一点N ，使得45BCO BNO ∠+∠=︒，若存在，请求出点N 的坐标；若不存在，请说明理由．20．已知二次函数2(0)y x bx c a =++≠的图像与x 轴的交于A 、(1,0)B 两点，与y 轴交于点(0,3)C -．(1)求二次函数的表达式及A 点坐标；(2)D 是二次函数图像上位于第三象限内的点，求点D 到直线AC 的距离取得最大值时点D 的坐标；(3)M 是二次函数图像对称轴上的点，在二次函数图像上是否存在点N ．使以M 、N 、B 、O 为顶点的四边形是平行四边形？若有，请写出点N 的坐标（不写求解过程）．答案1．(1)2y x 2x 3=-++(2)()0,3C 、()1,0B -(3)32．(1)223y x x =-- (2)254(3)存在，点P 的坐标为(12)或(12)+或()12-或(12)-3．(1)2y x 2x 3=-++(2)P 点坐标115(,)24或(2,3)(3)F 点坐标为：(1,0)、(5,0)、)2,0、()2-4．(1)y ＝﹣43x 2﹣83x +4 (2)S 最大＝252，D （﹣32，5） (3)存在，Q （﹣2，198）5．(1)抛物线解析式为y =-12x 2+x +4； (2)14DE AE =； (3)∠PCO 的正切值13或3．6．(1)223y x x =+-(2)()14P --，或()23--，(3)存在，坐标为⎝⎭或⎝⎭或或(-7．(1)2142y x x =+- (2)24=--S m m ，4(3)()4,4Q -或(2-+-或(2--+或()4,4-8．(1)2+23y x x =-+(2)P 1（32，154），P 2（2，3）(3)存在点M 其坐标为1M 43539（，）或2M9．(1)241y x x =-++ (2)274(3)存在，E （4，3）或（-2，5）或（-3，2）或（3，0）．10．(1)223y x x =--(2)1或1-(3)在抛物线上存在点3(4P -，15)16-，使直线PB 恰好将四边形AECF 的周长和面积同时平分11．(1)y ＝﹣12x 2+4x ﹣6，y ＝32x ﹣6 (2)152(3)存在，点Q 的坐标为（4，﹣2）12．(1)（1）y =-14x 2+x +3，y =12x +1 (2)274(3)(1,154)(2)232,39P ⎛⎫ ⎪⎝⎭(3)①y x =； 14．(1)A (－2，0)，B (4，0)，C (0，4)，24y x =+(2)(2，4)(3)存在，(－23，289)或(－6，－20)15．(1)2142y x x =-- (2)3(3)FAOB S 四边形有最大值12，此时点F 的坐标为()2,4-(4)存在，点Q 的坐标()18,2Q -，()26,6Q -，()35,3Q -，()41,1Q -16．(1)2142y x x =-- (2)191,2E ⎛⎫- ⎪⎝⎭；E 2（2，-4） (3)存在，（8，20）17．(1)y ＝－x 2＋3x ＋4(2)P （2，6）；四边形OCPE 的面积最大为16(3)存在； M 113,28⎛⎫- ⎪⎝⎭或M 252728,⎛⎫ ⎪⎝⎭或M 355,22⎛⎫- ⎪⎝⎭或M 453,22⎛⎫- ⎪⎝⎭18．(1)211242y x x =-++ (2)2(3)34m -≤-或32m -≤(2)（-2，-3）或（-1，-4）(3)（0，2）或（0，-2）20．(1)223y x x =+-，(3,0)A - (2)315,24D ⎛⎫-- ⎪⎝⎭(3)存在，(2,3)--或(0,3)-或(2,5)。

中考数学复习考点知识讲解与练习专题30 二次函数中的面积问题进入函数学习以后，面积问题在一直是学习中的一个重点，常考点，因此在二次函数的面积问题必然是中考复习中的一个重要内容，其面积往往有直接计算，割补法计算等，其中基本图形有以下几种：当然，更多的时候利用铅垂高度与水平宽度的一半进行运用，更显方便；通过本中考数学复习考点知识讲解与练习专题的巩固训练，让学生对二次函数的面积问题能形成良好的才思考方法，学会观察、分析、比较、总结，掌握二次函数面积相关问题的计算方法。

1．正方形的边长为3，边长增加x，面积增加y，则y关于x的函数解析式为（）A．2y(x3)=+B．2y x9=+C．26y x x=+D．2312y x x=+2．正方体的棱长为x，表面积为y，则y与x之间的函数关系式为（）A．16y x=B．6y x=C．26y x=D．6yx=3．如图ABC和DEF都是边长为2的等边三角形，它们的边,BC EF在同一条直线l上，点C ，E 重合，现将ABC ∆沿着直线l 向右移动，直至点B 与F 重合时停止移动．在此过程中，设点移动的距离为x ，两个三角形重叠部分的面积为y ，则y 随x 变化的函数图像大致为（）A ．B ．C ．D ．4．将抛物线y=x 2-4x+1向左平移至顶点落在y 轴上，如图所示，则两条抛物线、直线y=-3和x 轴围成的图形的面积S （图中阴影部分）是（）A ．4B ．5C ．6D ．75．抛物线234y x x =--与x 轴交于A 、B ，与y 轴交于C 点，则△ABC 的面积为（）A ．3B ．4C ．10D ．126．下列图形中阴影部分的面积相等的是（）A ．②③B ．③④C ．①②D ．①④7．如图，抛物线y ＝﹣2x 2+2与x 轴交于点A 、B ，其顶点为E ．把这条抛物线在x 轴及其上方的部分记为C 1，将C 1向右平移得到C 2，C 2与x 轴交于点B 、D ，C 2的顶点为F ，连结EF ．则图中阴影部分图形的面积为( )A ．1B ．2C ．3D ．48．如图，在等腰Rt ABC 中，90C ∠=︒，直角边AC 长与正方形MNPQ 的边长均为2,cm CA 与MN 在直线l 上．开始时A 点与M 点重合，让ABC 向右平移，直到C 点与N 点重合时为止，设ABC 与正方形MNPQ 重叠部分(图中阴影部分)的面积为2ycm ，MA 的长度为xcm ，则y 与x 之间的函数关系大致是( )A ．B ．C ．D ．9．如图，矩形ABCD 中，AB ＝2AD ＝4cm ，动点P 从点A 出发，以1cm /s 的速度沿线段AB 向点B 运动，动点Q 同时从点A 出发，以2cm /s 的速度沿折线AD →DC →CB 向点B 运动，当一个点停止时另一个点也随之停止．设点P 的运动时间是x （s ）时，△APQ 的面积是y （cm 2），则能够反映y 与x 之间函数关系的图象大致是（）A ．B ．C ．D ．10．如图，用长为24m 的篱笆围成一面利用墙（墙的最大可用长度a 为9m ）、且中间隔有一道篱笆的长方形花圃，则围成的花圃的面积最大为（）A ．48 m 2B ．45m 2C ．16 m 2D ．44m 211．如图，等腰()90Rt ABC ACB ∠=的直角边与正方形DEFG 的边长均为2，且AC 与DE 在同一直线上，开始时点C 与点D 重合，让ABC 沿这条直线向右平移，直到点A 与点E 重合为止．设CD 的长为x ，ABC 与正方形DEFG 重合部分(图中阴影部分)的面积为y ，则y 与x 之间的函数关系的图象大致是（）A ．B ．C ．D ．12．如图，在直角坐标系的第一象限内，AOB 是边长为2的等边三角形，设直线:(02)=l x t t 截这个三角形所得位于直线左侧的图形（阴影部分）的面积为S ，则S 关于t 的大致函数图象是（ ）A ．B ．C ．D ．13．如图，在ABC 中，90ACB ∠=︒，4AC =，3BC =．线段PE 的两个端点都在AB 上，且1PE =，P 从点A 出发，沿AB 方向运动，当E 到达点B 时，P 停止运动，在整个运动过程中，空白部分面积DPEC S 四边形的大小变化的情况是（）A ．一直减小B ．一直增大C ．先增大后减小D ．先减小后增大14．如图，在Rt DEF △中，90EFD ∠=︒，30DEF ∠=︒，3EF cm =，边长为2cm 的等边ABC 的顶点C 与点E 重合，另一个顶点B （在点C 的左侧）在射线FE 上．将ABC 沿EF 方向进行平移，直到A 、D 、F 在同一条直线上时停止，设ABC 在平移过程中与DEF 的重叠面积为2ycm ，CE 的长为x cm ，则下列图象中，能表示y 与x 的函数关系的图象大致是（）．A ．B ．C ．D ．15．如图，四边形ABCD 是矩形，AB=4，BC=6，点O 是线段BD 上一动点，EF 、GH 过点O ，EF∥AB，交AD 于点E ，交BC 于点F ，GH∥BC，交AB 于点G ，交DC 于点H ，四边形AEOG的面积记为S，GB=a，则S关于a的函数关系图象是（）A．B．C．D．16．某农场用篱笆围成饲养室，一面靠现有墙(墙足够长)，现有四种方案供选择(如图)：A方案为一个封闭的矩形；B方案为一个等边三角形，并留一处1m宽的门；C方案为一个矩形，中间用一道垂直于墙的篱笆隔开，并在如图所示的三处各留1m宽的门；D方案为一个矩形，中间用一道平行于墙的篱笆隔开，并在如图所示的四处各留1m宽的门．已知计划中的篱笆(不包括门)总长为12m，则能建成的饲养室中面积最大的方案为()A．B．C．D．17．如图，4AB 为半圆的直径，动点P为AB上，点P从点A出发，沿AB匀速运动到点B，速度为2，运动时间为t，分别以AP与PB为直径做半圆，则图中阴影部分的面积S与时间t之间的函数图象大致为（）．A ．B ．C ．D ．18．如图，ABC 和DEF 都是直角边长为的等腰直角三角形，它们的斜边AB ，DE 在同一条直线l 上，点B ，D 重合．现将ABC 沿着直线l 以2cm/s 的速度向右匀速移动，直至点A 与E 重合时停止移动．在此过程中，设点B 移动的时间为()s x ，两个三角形重叠部分的面积为()2cm y ，则y 随x 变化的函数图象大致为（）A ．B ．C ．D ．二、填空题19．用一根长为100cm 的铁丝围成一个矩形，则围成矩形面积的最大值是__________cm 2．20．如图，在平面直角坐标系中，抛物线2y x bx c =-++经过坐标原点O ，与x 轴的另一个交点为A ，且5OA =，过抛物线的顶点B 分别作BC x ⊥轴于C 、BD y ⊥轴于D ，则图中阴影部分图形的面积的和为______．21．已知，四边形ABCD 的两条对角线AC 、BD 互相垂直，且AC +BD ＝10，当AC ＝_______时，四边形ABCD 的面积最大，最大值为__________．22．如图，ABC ∆为一块铁板余料，10BC =cm ，高AD=10cm ，要用这块余料裁出一个矩形PQMN ，使矩形的顶点P ，N 分别在边上AB ，AC 上，顶点Q ，M 在边上BC 上，则矩形PQMN 面积的最大为_________2cm ．23．如图，在Rt ABC 中，90BAC ∠=︒，AB AC ==AD 为BC 边上的高，动点P 在AD 上，从点A 出发，沿A D →方向运动，设AP x =，ABP △的面积为1S ，矩形PDFE 的面积为2S ，12y S S =+，则y 与x 的关系式是________．24．如图，边长为2的正方形ABCD 的中心在直角坐标系的原点O ，AD ∥x 轴，以O 为顶点且过A 、D 两点的抛物线与以O 为顶点且经过B 、C 两点的抛物线将正方形分割成几部分，则图中阴影部份的面积是______________．25．如图，在平面直角坐标系中，抛物线212y x =经过平移得到抛物线2122y x x =-，其对称轴与两段抛物线所围成的阴影部分的面积是_______26．如图，点P 是双曲线C ：y ＝4x (x ＞0)上的一点，过点P 作x 轴的垂线交直线AB ：y ＝12x ﹣2于点Q ，连结OP ，OQ ．当点P 在曲线C 上运动，且点P 在Q 的上方时，△POQ 面积的最大值是_____．27．如图，坐标平面上，二次函数24y x x k =-+-的图形与x 轴交于A 、B 两点，与y 轴交于C 点，其顶点为D ，且0k >．若ABC ∆与ABD ∆的面积比为1:3，则k 值为________．28．如图，将抛物线y=−12x2平移得到抛物线m．抛物线m经过点A（6，0）和原点O，它的顶点为P，它的对称轴与抛物线y=−12x2交于点Q，则图中阴影部分的面积为______．29．如图，A、B为抛物线y＝x2上的两点，且AB//x轴，与y轴交于点C，以点O为圆心，OC为半径画圆，若AB＝，则图中阴影部分的面积为___30．已知二次函数y=2x2的图象如图所示，将x轴沿y轴向上平移2个单位长度后与抛物线交于A、B两点，则△AOB的面积为____.31．已知二次函数y=x 2－2x －3与x 轴交于A 、B 两点，在x 轴上方的抛物线上有一点C ，且△ABC 的面积等于10，则C 点坐标为________．32．如图，在平面直角坐标系中，过点(,0)P x 作x 轴的垂线，分别交抛物线22y x =+与直线y x =-交于点A ，B ，以线段AB 为对角线作菱形ACBD ，使得60D ︒∠=，则菱形ACBD 的面积最小值为______．33．如图，有一块三角形土地，它的底边100BC m =，高80AH m =，某房地产公司沿着地边BC 修一座底面是矩形DEFG 的大楼，当这座大楼的地基面积最大时，这个矩形的宽是________m ．34．如图，在等边三角形ABC 中，6,AB D =是线段BC 上一点，以AD 为边在AD 右侧作等边三角形ADE ，连结CE ．（1）若2CD =时，CE =_________（2）设BD a =，当EDC ∆的面积最大时，a =__________．35．在平面直角坐标系中，抛物线23y ax bx a =+-经过(1,0)-和(0,3)两点，直线1y x =+与抛物线交于A ，B 两点，P 是直线AB 上方的抛物线上一动点，当ABP △的面积最大值时，点P 的横坐标为___________．三、解答题36．如图，正方形ABCD 的边长为4，点E 在AB 边上，1BE =，F 为BC 的中点．将正方形截去一个角后得到一个五边形AEFCD ，点P 在线段EF 上运动（点P 可与点E ，点F 重合），作矩形PMDN ，其中M ，N 两点分别在CD ，AD 边上．设CM x =，矩形PMDN 的面积为S ．（1）DM =__________（用含x 的式子表示），x 的取值范围是__________；（2）求S 与x 的函数关系式；（3）要使矩形PMDN 的面积最大，点P 应在何处？并求最大面积．37．如图，在ABC 中，∠B=90°，AB=8米，BC=10米，动点P 从点A 开始沿边AB 向B 以1米/秒的速度运动(不与点B 重合)，动点Q 从点B 开始沿BC 向C 以2米/秒的速度运动(不与点C 重合)，如果P ，Q 分别从A ，B 同时出发，设运动时间为x 秒，BPQ 的面积为y 平方米（1）填空：BQ=米，BP=米(用含x 的代数式表示)（2）求y 与x 之间的函数关系式，并求出当x 为多少时y 有最大值，最大值是多少？38．如图，某小区为美化生活环境，拟在一块空地上修建一个花圃，花圃形状如图所示．已知A D ∠=∠90=︒，120C ∠=︒，其中AD DC 、两边靠墙，另外两边由20米长的栅栏围成．设BC x =米，花圃的面积为y 平方米．（1）用含有x 的代数式表示出DC 的长；（2）求这块花圃的最大面积．39．如图，已知一次函数28y x =-与抛物线2y x bx c =++都经过x 轴上的A 点和y 轴上的B 点．（1）求抛物线的解析式；（2）若抛物线的顶点为D ，试求出点D 的坐标和△ABD 的面积；（3）M 是线段OA 上的一点，过点M 作MN x ⊥轴，与抛物线交于N 点，若直线AB 把△MAN 分成的两部分面积之比为1∶3，请求出N 点的坐标．40．如图，在平面直角坐标系中，抛物线2y x bx c =++与x 轴交于A ，B 两点，与y 轴交于点C ，已知(3,0)B ，(0,3)C -，连接BC ，点P 是抛物线上的一个动点，点N 是对称轴上的一个动点．（1）求该抛物线的函数解析式．（2）当PAB的面积为8时，求点P的坐标．（3）若点P在直线BC的下方，当点P到直线BC的距离最大时，在抛物线上是否存在点Q，使得以点P，C，N，Q为顶点的四边形是平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．。

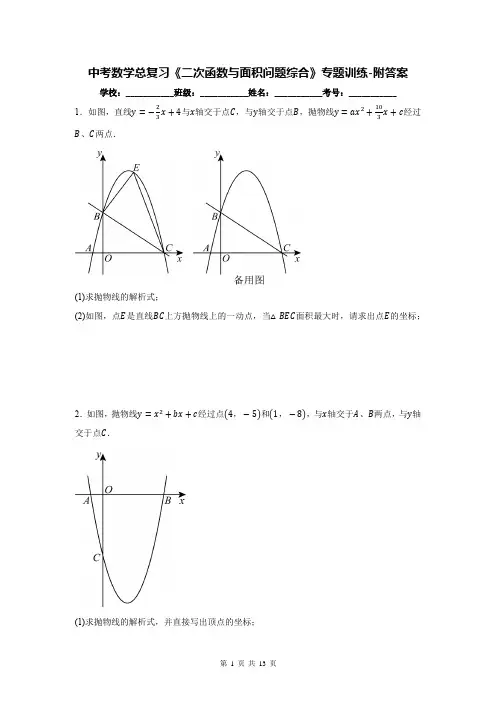
中考数学总复习《二次函数与面积问题综合》专题训练-附答案学校：___________班级：___________姓名：___________考号：___________1．如图，直线y=−23x+4与x轴交于点C，与y轴交于点B，抛物线y=ax2+103x+c经过B、C两点．(1)求抛物线的解析式；(2)如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标；2．如图，抛物线y=x2+bx+c经过点(4，−5)和(1，−8)，与x轴交于A、B两点，与y轴交于点C．(1)求抛物线的解析式，并直接写出顶点的坐标；(2)连接AC、BC，求△ABC的面积；(3)若点P是抛物线y=x2+bx+c上一点（点P不与点C重合），且S△ABP=S△ABC，则点P的坐标为．3．如图，抛物线y=ax2+bx−4与x轴交于A(−3，0)、B(4，0)两点，与y轴交于点C．(1)求抛物线解析式；(2)点H是抛物线对称轴上的一个动点，连接AH、CH，求出△ACH周长的最小值时点H的坐标；(3)若点G是第四象限抛物线上的动点，求△BCG面积的最大值以及此时点G的坐标；4．如图，已知抛物线y=ax2+bx+5经过A(−5,0)，B(−4,−3)两点，与x轴的另一个交点为C．(1)求该抛物线的解析式；(2)若该抛物线顶点为P，求△BPC的面积．注：抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=−b2a ，顶点坐标是(−b2a,4ac−b24a)．5．如图1，在平面直角坐标系中，已知抛物线y=ax2+bx+4经过点A(−2,0)，B(6,0)与y 轴交于点C．(1)直接写出该抛物线的表达式；(2)设抛物线的顶点为P，连接BC，PC，PB，求△PCB的面积；(3)如图2，抛物线的对称轴l交x轴于点E，若点Q为x轴上方、对称轴l右侧抛物线上的一动点，过点Q作直线AQ，BQ分别交对称轴l于点M，N，当ME=13MN时，求点Q的坐标．6．在平面直角坐标系中∠ACB=90°，AB∥x轴．如图1，C(1,0)，AB=5且OC:OA=1:2．(1)求点A、点B的坐标；(2)已知抛物线y=ax2+bx+c(a≠0)过A、B、C三点，求该抛物线的表达式；(3)如图2，抛物线对称轴与AB交于点D，现有一点P从点A出发，以每秒1个单位的速度在AB上向点B运动，另一点Q从点D与点P同时出发，以每秒5个单位在抛物线对称轴上运动．当点P到达B点时，点P、Q同时停止运动，问点P、Q运动到何处时，△PQB面积最大，并求出最大面积．7．如图，在平面直角坐标系xOy中，直线l：y=x−2与x轴，y轴分别交于点A，B，抛物线y=x2+bx+c经过点B，且与直线l的另一个交点为C(8,n)．(1)求n的值和抛物线的解析式．(2)已知P是抛物线上位于直线BC下方的一动点（不与点B，C重合），设点P的横坐标为a．当a为何值时，△BPC的面积最大，并求出其最大值．(3)在抛物线上是否存在点M，使△BMC是以BC为直角边的直角三角形？若存在，直接写出点M的坐标；若不存在，请说明理由．8．如图，抛物线y=−x2+bx+c与x轴交于A(1，0)，B(−3，0)两点，与y轴交于点C，P是抛物线上一动点．(1)求抛物线的解析式；(2)当点P在直线BC上方的抛物线上时，求△PBC的最大面积，并直接写出此时P点坐标；(3)若点M在抛物线的对称轴上，以B，C，P，M为顶点、BC为边的四边形能否是平行四边形？若能，请直接写出点P的坐标；若不能，请说明理由．9．如图，对称轴为x=−1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A，B两点，其中点A的坐标为(−3,0)．(1)求点B的坐标；(2)已知a=1，C为抛物线与y轴的交点；①若点P在抛物线上，且S△POC=4S△BOC，求点P的坐标；①设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．10．综合与探究如图，在平面直角坐标系中，抛物线y=ax2−x+c与y轴交于点A(0,−4)，与x轴交于点B(4,0)，连接AB.(1)求抛物线的解析式．(2)P是AB下方抛物线上的一动点，过点P作x轴的平行线交AB于点C，过点P作PD⊥x轴于点D．①求PC+PD的最大值．①连接PA，PB是否存在点P，使得线段PC把△PAB的面积分成3:5两部分？若存在，请直接写出点P的坐标；若不存在，请说明理由．11．如图，在平面直角坐标系中，抛物线y=x2+bx+c经过A(−1,0)、C(0,−3)两点，且与x轴交于另一点B（点B在点A右侧）．(1)求抛物线的解析式；(2)若点M是线段BC上一动点，过点M的直线ED平行y轴交x轴于点D，交抛物线于点E，求△BCE面积的最大值及此时点M的坐标；(3)在（2）的条件下：当△BCE的面积取得最大值时，在x轴上是否存在这样的点P，使得以点M，B，P为顶点的三角形是等腰三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．x2+bx+c的图象经过点A(0，3)，与x轴12．如图，在直角坐标系中，二次函数y=−14的一个交点为(−2，0)，过点A作AB∥x轴交抛物线于点B．设抛物线的顶点为C，连接AC,BC．(1)求二次函数的表达式；(2)在抛物线上，是否存在一点D，使得S△ABD=S△ABC若存在，求出点D的坐标；若不存在，请说明理由；(3)连接OC．在线段AB是否存在一点M，使得以M,A,C为顶点的三角形与△AOC相似？若存在，求出点M的坐标；若不存在，请说明理由．13．如图1，抛物线y=ax2+bx+4与x轴交于点A(−2,0)，B(4,0)与y轴交于点C，在抛物线上有一动点P，连接PA、PB、PC、BC．(1)求该抛物线的函数解析式；(2)若点P在第一象限的抛物线上，当△BCP的面积是3时，求△ABP的面积；(3)如图2，连接AC，点D在线段AC上，过D作DE⊥AB于点E，点F在线段BC上，且D，F两点关于y轴上的某点成中心对称，连接DF，EF试探究线段EF的长度是否有最小值？如果有请求出这个最小值；若没有请说明理由．14．如图，已知二次函数y=−x2+bx+c的图象与x轴交于点A(−4,0)和点B，与y轴相交于点C(0,4)．(1)求该二次函数的解析式；(2)点D 在线段OA 上运动，过点D 作x 轴的垂线，与AC 交于点Q ，与抛物线交于点P ． ①连接AP 、CP ，当四边形AOCP 的面积最大时，求此时点P 的坐标和四边形AOCP 面积的最大值；①探究是否存在点P 使得以点P 、C 、Q 为顶点的三角形与△ADQ 相似？若存在，求出点P 的坐标；若不存在，说明理由．15．如图1，抛物线C 1：y =14x 2+c 经过点P (2,a )，且与x 轴交于点A (−4,0)、B (4,0)两点．(1)求点P 的坐标；(2)将线段OP 绕点O 逆时针旋转45°后得到OQ ，若直线OQ 与抛物线C 1相交于点T ，求点T 的横坐标；(3)将抛物线C 1平移至抛物线C 2，使其顶点在原点O 处，如图2所示，过点F (0,1)的直线与抛物线相交于C 、D 两点，分别过C 、D 向直线y =−1作垂线，垂足为M 、N ，连接FM 、FN ，记△CMF 的面积为S 1，△MNF 的面积为S 2，△DNF 的面积为S 3，试求S 22S 1S 3的值．参考答案：1．(1)y =−23x 2+103x +4(2)E(3，8)2．(1)y =x 2−4x −5，顶点坐标为(2，−9)(2)15(3)(4，−5) (2+√14，5) (2−√14，5)3．(1)y =13x 2−13x −4 (2)H (12,−3.5) (3)△BCG 面积的最大值为83，此时G (2,−103)4．(1)y =x 2+6x +5(2)S △BCP =35．(1)y =−13x 2+43x +4(2)8(3)Q (225,25675)6．(1)A(0,2) B (5,2)(2)y =12x 2−52x +2(3)当点P 的坐标为( 52，2)，点Q 的坐标为( 52 ,292 )或( 52 , −212 )时，△PQB 面积最大，最大面积为12587．(1)n =6 y =x 2−7x −2；(2)当a =4时，△BPC 的面积最大，最大值为64；(3)存在点M ，使△BMC 是以BC 为直角边的直角三角形，此时点M 的坐标为(6,−8)或(−2,16)8．(1)y =−x 2−2x +3(2)△PBC 的最大面积为278，点P 的坐标为（﹣32，154）(3)能，点P(−4，−5)或(2，−5)9．(1)(1,0)(2)①(4,21)或(−4,5)；①9410．(1)y =12x 2−x −4(2)① PC +PD 取得最大值254 ① (3,−52)或 (1+√6,−32)11．(1)y =x²−2x −3；(2)278 M (32，−32)；(3)(0，0)或(6−3√22，0)或(32，0)或(6+3√22，0)．12．(1)y =−14x 2+x +3； (2)存在点D ，(2+2√2，2)或(2−2√2，2)；(3)存在点M ，点M 的坐标为(103，3)或(32，3)．13．(1)y =−12x 2+x +4；(2)272或152；(3)有，最小值为8√55．14．(1)y =−x 2−3x +4(2)①当t =−2时，S 四边形AOCP 有最大值，最大值为16，P (−2,6)；①存在，点P 的坐标为(−3,4)或(−2,6)15．(1)(2,−3)(2)−2+2√1015或−2−2√1015(3)4。

二次函数中面积问题的两种考法类型一、面积最值问题 例．抛物线2y x bx c =−++交x 轴于点(4,0)A ，交y 轴于点(0,4)B ．(1)求抛物线的解析式，并直接写出抛物线的对称轴和另一个与x 轴交点C 的坐标；(2)直接写出当0y <时，x 的取值范围．(3)如图，点P 是线段AB 上方抛物线上一动点，当P 点的坐标为_______时，PAB 的面积最大．【答案】(1)234y x x =−++；(1,0)C −；对称轴直线32x = (2)1x <−或>4x(3)()2,2【分析】（1）用待定系数法求函数的解析式即可；（2）根据函数图象即可得出结论；（3）过点P 作PG y ∥轴交AB 于点G ，设2(,34)P t t t −++，则(,4)G t t −+，则22(2)8PAB S t =−−+，再由此求解即可．【详解】（1）将点(4,0)A ，(0,4)B 代入2y x bx c =−++，∴16404b c c −++=⎧⎨=⎩，解得34b c =⎧⎨=⎩，234y x x ∴=−++；令0y =，得2034x x =−++解得：121;4x x =−=∴(1,0)C −，(4,0)A对称轴直线322b x a =−=（2）由（1）得：(1,0)C −，(4,0)A∴当1x <−或>4x 时，0y <（3）设直线AB 的解析式为y kx m =+，∴404k m m +=⎧⎨=⎩，解得14k m =−⎧⎨=⎩，4∴=−+y x ，过点P 作PG y ∥轴交AB 于点G ，设2(,34)P t t t −++，则(,4)G t t −+，223444PG t t t t t ∴=−+++−=−+，2214(4)2(2)82PAB S t t t ∆∴=⨯⨯−+=−−+，当2t =时，PAB 的面积有最大值8，此时(2P ，2)．故答案为：()2,2．【点睛】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，胡不归求最短距离的方法是解题的关键． 【变式训练1】如图，抛物线2(1)y x k =++与x 轴相交于A 、B 两点，与y 轴相交于点(0,3)C −．(1)求抛物线的对称轴及k 值；(2)抛物线的对称轴上存在一点P ，使得PA PC +的值最小，求此时点P 的坐标；(3)点M 是抛物线上一动点，且在第三象限，当M 点运动到何处时，四边形AMCB 的面积最大？求出四边形AMCB 的最大面积．【答案】(1)1,4x k =−=−(2)(1,2)P −−(3)315,24M ⎛⎫− ⎪⎝⎭，S 最大，最大值为758【分析】（1）根据解析式可得抛物线的对称轴为直线=1x −，将点(0,3)C −代入解析式，待定系数法即可求解；（2）连接AC ，交对称轴于点P ，根据两点之间，线段最短可得点P 即为所求，求得直线AC 的解析式，令=1x −，即可求解；（3）连接OM ，如图1，设M 点坐标为()2,(1)4x x +−，根据AMO CMO CBO AMCB S S S S =++四边形△△△23375228x ⎛⎫=−++ ⎪⎝⎭，根据二次函数的性质即可求解．【详解】（1）解：抛物线2(1)y x k =++的对称轴为直线=1x −，把(0,3)C −代入2(1)y x k =++得31k −=+，4k ∴=−；（2）连接AC ，交对称轴于点P ，∵两点之间，线段最短，∴PA PC +的最小值为AC 的长，则点P 即为所求对于2y (x 1)4=+−，令0y =，则2(1)40x +-=，解得11x =，23x =−，A ∴点坐标为(3,0)−，B 点坐标为(1,0)，设直线AC 的关系式为：y mx b =+，把(3,0)A −，(0,3)C −代入y mx b =+，得303m b b −+=⎧⎨=−⎩，解得13m b =−⎧⎨=−⎩，∴直线AC 的关系式为3y x =−−，当=1x −时，132y =−=−，P ∴点坐标为(1,2)−−；（3）连接OM ，如图1，设M 点坐标为()2,(1)4x x +−，AMO CMO CBO AMCB S S S S =++四边形△△△111222m m AO y CO x OC BO ⨯⨯+⨯⨯+⨯⨯23114(1)3()31222x x ⎡⎤=−++⨯⨯−+⨯⨯⎣⎦239622x x =−−+23375228x ⎛⎫=−++ ⎪⎝⎭， 当32x =−时，S 最大，最大值为758．【点睛】本题考查了二次函数的性质，面积问题，轴对称的性质，熟练掌握二次函数的性质是解题的关键． 【变式训练2】如图，抛物线22y ax x c =−+与x 轴交与()1,0A ，()3,0B −两点．(1)求该抛物线的解析式； (2)设抛物线交y 轴与C 点，在该抛物线的对称轴上是否存在点Q ，使得QAC △的周长最小？若存在，求出Q 点的坐标；若不存在，请说明理由．(3)在第二象限内的抛物线上的是否存在一点P ，使PBC 的面积最大？若存在，求出点P 的坐标及PBC 的面积最大值；若不存在，请说明理由．【答案】(1)223y x x =−−+(2)存在，()1,2Q −；(3)存在，315,24P ⎛⎫− ⎪⎝⎭，PBC 的面积最大值是278【分析】（1）利用待定系数法即可求得二次函数的解析式；（2）根据题意可知，边AC 的长是定值，要想AQC 的周长最小，即是 AQ CQ +最小所以此题的关键是确定点Q 的位置，找到点A 关于对称轴的对称点B ，利用待定系数法求出直线BC 的解析式，直线BC 与对称轴的交点即是所求的点Q ；（3）首先求得BC 的坐标，然后设P 的横坐标是x ，利用a 表示出PBC 的面积，利用二次函数的性质求解；【详解】（1）根据题意得：10930b c b c −++=⎧⎨−−+=⎩，解得23b c =−⎧⎨=⎩，则抛物线的解析式是223y x x =−−+；（2）理由如下：由题知A 、B 两点关于抛物线的对称轴=1x −对称，∴直线BC 与=1x −的交点即为Q 点，此时AQC 周长最小，对于223y x x =−−+，令0x =，则3，故点()0,3C ，设BC 的解析式是y mx n =+，则303m n n −+=⎧⎨=⎩，解得13m n =⎧⎨=⎩，则BC 的解析式是3y x =+．=1x −时，132y =−+=，∴点Q 的坐标是()1,2Q −；（3）过点P 作y 轴的平行线交BC 于点D ，设P 的横坐标是x ，则P 的坐标是()2,23x x x −−+，对称轴与BC 的交点D 是(),3x x +．则()()222333PD x x x x x=−−+−+=−． 则()222139332733222228PBC S x x x x x ⎛⎫=−−⨯=−−=−++ ⎪⎝⎭△， ∵302−<，故PBC 的面积有最大值是278．【点睛】本题考查了待定系数法求函数的解析式以及二次函数的性质，求最值问题一般是转化为函数最值问题求解. (1)求二次函数的表达式；(2)如图1，求AOD △周长的最小值；(3)如图2，过动点D 作DP AC ∥交抛物线第一象限部分于点P ，连接,PA PB ，记PAD 与PBD △的面积和为S ，当S 取得最大值时，求点P 的坐标，并求出此时S 的最大值．【答案】(1)21262y x x =−++(2)12(3)153,2⎛⎫ ⎪⎝⎭，272S =最大值 【分析】（1）根据题意设抛物线的表达式为()()26y a x x =+−，将()0,6代入求解即可；（2）作点O 关于直线BC 的对称点E ，连接EC EB 、，根据点坐特点及正方形的判定得出四边形OBEC 为正方形，()6,6E ，连接AE ，交BC 于点D ，由对称性DE DO =，此时DO DA +有最小值为AE 的长，再由勾股定理求解即可；（3）由待定系数法确定直线BC 的表达式为6y x =−+，直线AC 的表达式为36y x =+，设21,262P m m m ⎛⎫−++ ⎪⎝⎭，然后结合图形及面积之间的关系求解即可．【详解】（1）解：由题意可知，设抛物线的表达式为()()26y a x x =+−， 将()0,6代入上式得：()()60206a =+−，12a =−所以抛物线的表达式为21262y x x =−++；（2）作点O 关于直线BC 的对称点E ，连接EC EB 、，∵()6,0B ，()0,6C ，90BOC ∠=︒，∴6OB OC ==，∵O 、E 关于直线BC 对称，∴四边形OBEC 为正方形，∴()6,6E ，连接AE ，交BC 于点D ，由对称性DE DO =， 此时DO DA +有最小值为AE 的长，10AE ===∵AOD △的周长为DA DO AO ++，2AO =，DA DO +的最小值为10，∴AOD △的周长的最小值为10212+=；（3）由已知点()2,0A −，()6,0B ，()0,6C ，设直线BC 的表达式为y kx b =+，将()6,0B ，()0,6C 代入y kx b =+中，600k b b +=⎧⎨=⎩，解得16k b =−⎧⎨=⎩，∴直线BC 的表达式为6y x =−+，同理可得：直线AC 的表达式为36y x =+，∵PD AC ∥，∴设直线PD 表达式为3y x a =+，由（1）设21,262P m m m ⎛⎫−++ ⎪⎝⎭，代入直线PD 的表达式得：2162a m m =−−+，∴直线PD 的表达式为：21362y x m m =−−+， 由261362y x y x m m =−+⎧⎪⎨=−−+⎪⎩，得22118411684x m m y m m ⎧=+⎪⎪⎨⎪=−−+⎪⎩，∴221111,68484D m m m m ⎛⎫+−−+ ⎪⎝⎭， ∵P ，D 都在第一象限，∴PAD PBD PAB DAB S S S S S =+=−△△△△2211112662284AB m m m m ⎡⎤⎛⎫⎛⎫=−++−−−+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 21398284m m ⎛⎫=⨯−+ ⎪⎝⎭()22339622m m m m =−+=−−2327(3)22m =−−+， ∴当3m =时，此时P 点为153,2⎛⎫ ⎪⎝⎭.272S =最大值．【点睛】题目主要考查二次函数的综合应用，包括待定系数法确定函数解析式，周长最短问题及面积问题，理解题意，熟练掌握运用二次函数的综合性质是解题关键．类型二、求面积问题 例．已知：m ，n 是方程2650x x −+=的两个实数根，且m n <，抛物线2y x bx c =−++的图象经过点(,0)(0,)A m B n ，．(1)求这个抛物线的解析式；(2)设（1）中的抛物线与x 轴的另一交点为C ，抛物线的顶点为D ，试求BCD △的面积；(3)P 是线段OC 上的一点，过点P 作PH x ⊥轴，与抛物线交于H 点，若直线BC 把PCH △分成面积之比为2:3的两部分，请求出P 点的坐标．【答案】(1)245y x x =−−+(2)15(3)点( 1.5,0)P -或2(,0)3P −【分析】（1）利用因式分解法求出一元二次方程的解，从而得到点A B ，的坐标，再代入抛物线解析式即可解答；（2）令抛物线解析式中0y =，可求得点C 坐标，利用公式法求出顶点D 的坐标，过点D 作x 轴的垂线，垂足为点E ，分别求出CDE 、梯形DEOB 、BCO 的面积，利用BCD S △=CDE S +BCO DEOB S S 梯形−解答即可；（3）先利用待定系数法求得直线BC 的解析式，再设直线BC 与PH 相交于点F ，点(,0)P a ，则点2(5),(,45)F a a H a a a +--+，，从而求得25,5PF a FH a a =+=--，最后分两种情况讨论①当:2:3PF HF =时或②当:2:3HF PF =时，分别计算解答即可．【详解】（1）解：2650x x −+=(1)(5)0x x ∴−−=10,50x x ∴−=−=1,5x x ∴==m ，n 是方程2650x x −+=的两个实数根，且m n <，1,5m n ∴==(1,0)(0,5)A B \，把点(1,0)(0,5)A B ，代入抛物线解析式得105b c c −++=⎧⎨=⎩，解得45b c =−⎧⎨=⎩，245y x x \=--+；（2）解：2245=(2)9y x x x =--+-++Q(2,9)D \-令0y =23x ∴+=±1,5x x \==-(5,0)C ∴−如图，过点D 作x 轴的垂线，垂足为点E ，(2,0)E ∴−BCD S △=CDE S +BCO DEOB S S 梯形− 1()1222OB DE OE CE DE CO BO +×=×+-× 1(59)213955222+´=´´+-´´ 27251422=+-114=+15=；（3）解：如图，设直线BC 的解析式为5y kx =+，代入点(-5,0)C 得，550k −+= 1k ∴=5BC y x \=+设直线BC 与PH 相交于点F ，点(,0)P a则点2(5),(,45)F a a H a a a +--+，225,45(5)5PF a FH a a a a a \=+=--+-+=--直线BC 把PCH △分成面积之比为2:3的两部分，分两种情况讨论： ①当:2:3PF HF =时 252=53PF a FH a a +\=--，2210315a a a \--=+2213150a a \++=1.5a ∴=−（5a =−舍去），( 1.5,0)P \-②当:2:3HF PF =时252=53HF a a PF a --\=+ 23a ∴=−，2(,0)3P \- 综上所述，点( 1.5,0)P -或2(,0)3P −．【点睛】本题考查二次函数的图象与性质，涉及待定系数法求一次函数解析式、待定系数法求二次函数解析式、配方法求二次函数顶点坐标、解析法求线段的长等知识，利用等高三角形面积比等于底边比，掌握相关知识是解题关键．(1)当1m =时，求抛物线的顶点坐标；(2)若AC BC ⊥， ①求m 的值；②点P 是x 轴上方的抛物线上的一动点，连结．设PBC 的面积为数，试求点P 的坐标． 【答案】(1)28 ⎪⎝⎭，(2)①2m =；②22P ⎛ ⎝⎭或22P ⎛ ⎝⎭或()2,3P ． 【分析】（1）利用待定系数法可求解析式； （2）①根据题意得到()1,0A −，(),0B t ，()0,C m ，然后表示出22221AC OA OC m =+=+，()2222221BC OB OC m n =+=++，()2222AB n =+，根据AC BC ⊥利用勾股定理列方程求解即可；②过点P 作PH x ⊥轴于H ，交BC 于点Q ，先求出BC 的解析式，设点213,222P x x ⎛⎫−++ ⎪⎝⎭，则点1,22Q x x ⎛⎫−+ ⎪⎝⎭，由三角形面积公式可得12PBC S PG OB∆=，由二次函数的性质可求解．【详解】（1）解：∵点()1,0A −，在抛物线212y x nx m =−++图象上，1m =， ∴11021n m ⎧−−+=⎪⎨⎪=⎩，解得：121n m ⎧=⎪⎨⎪=⎩，∴抛物线解析式为：2211119122228y x x x ⎛⎫=−++=−−+⎪⎝⎭, ∴抛物线的顶点坐标为1928⎛⎫ ⎪⎝⎭，；（2）①解：当0y =时，即212x m −++=∴设(),0B t∵()1,0A −∴1212nt n −+=−=−∴21t n =+∴21OB n =+，21122AB n n =++=+ 当0x =时，y m = ∴()0,C m∴OC m =∴22221AC OA OC m =+=+，()2222221BC OB OC m n =+=++，()2222AB n =+∵AC BC ⊥∴222AC BC AB +=，∴()()222212122m m n n ++++=+∴整理得，2210m n −−=将()1,0A −代入212y x nx m =−++得，102n m −−+=可得，12n m =−，∴将12n m =−代入2210m n −−=，得212102m m ⎛⎫−−−= ⎪⎝⎭∴解得2m =或0（舍去） ∴2m =； ②∵2m =∴()0,2C ，()4,0B ，抛物线解析式为213222y x x =−++，∴设直线BC 的解析式为y kx b =+，代入B 、C 坐标得240b k b =⎧⎨+=⎩， 解得：12k =−，∴直线BC 的解析式为122y x =−+，过点P 作PH x ⊥轴于点H ，交BC 于点Q ，如图，设213,222P x x x ⎛⎫−++ ⎪⎝⎭，则1,22Q x x ⎛⎫−+ ⎪⎝⎭， ∴2213112222222PQ x x x x x⎛⎫=−++−−+=−+ ⎪⎝⎭，∴111222CPQ BPQS SSPQ OH PQ BH PQ OB =+=⋅+⋅=⋅()222112442422x x x x x ⎛⎫=−+⨯=−+=−−+ ⎪⎝⎭； ∵102−<，∴抛物线开口向下， ∴4PBCS≤∵S 为正偶数 ∴2S =或4， ∴当2S =时，即()2242x −−+=，解得2x =∴22P ⎛ ⎝⎭或22P ⎛ ⎝⎭； 当4S =时，即()2244x −−+=，解得2x =∴()2,3P综上所述，点P的坐标为22P ⎛+ ⎝⎭或22P ⎛ ⎝⎭或()2,3P ． 【点睛】本题是二次函数综合题，考查了待定系数法求解析式，二次函数的性质，一次函数的性质，两点距离公式，利用参数列方程是本题的关键． 设PBC 的面积为求123PP P 的面积．【答案】(1)2222y x x =−−(2)P 的坐标为()2,3−(3)【分析】（1）待定系数法求解析式；（2）作C 关于x 轴的对称点C '，连接B C '，根据C ，C '关于x 轴对称，则2CBC ABC '∠=∠，结合已知条件得出PCB CBC ∠=∠'，得出CP BC '∥，求得直线BC '的解析式为122y x =−+，直线CP 解析式为122y x =−−，联立抛物线解析式，进而即可求解．（3）过点P 作PH x ⊥轴交直线BC 于点H ，过1P作PW x ⊥轴交23P P 于W ，求得直线BC 解析式为122y x =−，设132222P m m m ⎛⎫− ⎪⎝⎭，，则122H m m ⎛⎫− ⎪⎝⎭，，当P 在BC 下方时，2211312222222PH m m m m m⎛⎫⎛⎫=−−−−=−+ ⎪ ⎪⎝⎭⎝⎭，此时1(2,3)P −，当P 在BC 上方时，2213112222222PH m m m m m ⎛⎫=−−−−=− ⎪⎝⎭，得出()()23,23,23P P −，进而求得直线23P P 解析式为122y x =+，得出()2,3W ，则16PW=，进而根据三角形面积公式即可求解．【详解】（1）解：把(1,0)A −，(4,0)B 代入212y x bx c =−+得：12840b c b c ⎧++=⎪⎨⎪−+=⎩，解得322b c ⎧=⎪⎨⎪=−⎩， ∴抛物线的解析式为213222y x x =−−；（2）作C 关于x 轴的对称点C '，连接B C '，如图：在213222y x x =−−中，令0x =得2y =−，∴(0,2)C −，C ，C '关于x 轴对称，∴(0,2)C '，2CBC ABC '∠=∠，2PCB ABC ∠=∠， PCB CBC ∴∠=∠'，∴CP BC '∥，由(4B ，0)，(0,2)C '设直线BC '的解析式为12y k x =+， 则1042k =+，解得：112k =−,∴直线BC '的解析式为122y x =−+，设直线CP 解析式为12y x b=−+，把(0C ，2)−代入得：2b =−，∴直线CP 解析式为122y x =−−， 联立212213222y x y x x ⎧=−⎪⎪⎨⎪=−−⎪⎩得：02x y =⎧⎨=−⎩或23x y =⎧⎨=−⎩，P ∴的坐标为(2,3)−；（3）过点P 作PH x ⊥轴交直线BC 于点H ，过1P作PW x ⊥轴交23P P 于W ，如图：由(4B ，0)，(0C ，2)− 设直线BC 的解析式为22y k x =−，则2042k =−，解得：212k =∴直线BC 解析式为122y x =−设132222P m m m ⎛⎫− ⎪⎝⎭，，则122H m m ⎛⎫− ⎪⎝⎭， 当P 在BC 下方时，2211312222222PH m m m m m⎛⎫⎛⎫=−−−−=−+ ⎪ ⎪⎝⎭⎝⎭， ()222112442422S m m m m m ⎛⎫∴=⨯−+⨯−+=−− ⎪⎝=+⎭，10−<，∴当2m =时，S 取最大值4，此时1(2,3)P −； 当P 在BC 上方时，2213112222222PH m m m m m ⎛⎫=−−−−=− ⎪⎝⎭21124822S m m ⎛⎫∴=⨯−⨯= ⎪⎝⎭，解得2m =或2m =−∴()()23,23,23P P −设直线23P P 的解析式为y kx b =+，∴()()3232k b k b =+⎨=−+⎪⎩，解得：122k b ⎧=⎪⎨⎪=⎩，∴直线23P P 解析式为122y x =+，在122y x =+，令2x =得3y =，∴()2,3W ，∴16PW =，∴123PP P的面积为()()16222⨯⨯−−=【点睛】本题考查了二次函数的综合运用，角度问题，面积问题，扎实的计算是解题的关键．课后训练1．如图1，在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴分别交于()1,0A m −，()3,0B m −两点，其中点B 在原点左侧，与y 轴交于点()0,3C −．(1)求抛物线的解析式；(2)已知抛物线顶点为P ，点M 在第三象限的抛物线上， ①若直线CM 与直线BP 关于直线y x =对称，求点M 的坐标；②如图2，若直线2y x n =+与抛物线交于点D ，E ，1D E x x −<<，与抛物线线的对称轴l 交于点H ，若DM l ⊥，连接ME ，MH ，求S MEH △的取值范围．【答案】(1)223y x x =+− (2)①57,24M ⎛⎫−− ⎪⎝⎭②2S MEH ≤0＜△【分析】（1）根据点,A B 可求出b ，根据点C 可求出c ，即可求解；（2）①先求出直线BP 的解析式，根据题意即可得出直线CM 的解析式，进而可求出点M 的坐标；②建立S MEH△与n的关系即可求解． 【详解】（1）解：由()1,0A m −，()3,0B m −可得抛物线的对称轴为：直线()()1312m m x −+−==− 又对称轴为：直线21bx =−⨯故121b−=−⨯，解得2b =又抛物线与y 轴交于点()0,3C −3c ∴=−所以抛物线的解析式为：223y x x =+− （2）①解：令0y =，则2230x x +−=解得：121,3x x ==− 故()()1,0,3,0A B −()222314y x x x =+−=+−()1,4P ∴−−设直线BP 的解析式为：y mx n =+故有：304m n m n −+=⎧⎨−+=−⎩，解得：26m n =−⎧⎨=−⎩ 所以直线BP 的解析式为：26y x =−− 因为直线CM 与直线BP 关于直线y x =对称所以直线CM 的解析式为：12632x y y x =−−⇒=−−联立直线CM 与抛物线的解析式： 213223y x y x x ⎧=−−⎪⎨⎪=+−⎩解得：1250,2x x ==−当57,24x y =−=−故点57,24M ⎛⎫−− ⎪⎝⎭②解：由题意得：2223y x n y x x =+⎧⎨=+−⎩，解得12x x ==故()),D n En−因为直线2y x n =+与抛物线对称轴l 交于点H 结合（1）可得：()1,2H n −−+因为点D ，点M 关于抛物线对称轴l 对称 故M 的横坐标()(212M x =⨯−−()(()4S 1122222ME E H H MD y y n =⨯⨯−=⨯−⨯=−−△1D Ex x −<<1∴−＜解得：32n −≤＜- 2S MEH ≤0＜△【点睛】本题以二次函数作为背景，综合考查了二次函数的对称性、一次函数的解析式等相关知识点．最后一小问的数学建模思想是学生应该具备的能力．(1)若函数的图象与坐标轴．．．有两个公共点，且(2)如图，若函数的图象为抛物线，与:(04)l x m m =<<交于点P ，连接点E ．设PBE △的面积为1S ，CDE 的面积为①当点P 为抛物线顶点时，求PBC 的面积；②探究直线l 在运动过程中，S −是否存在最大值？若存在，【答案】(1)0或2或4−(2)①6，②存在，163【分析】（1）根据函数与坐标轴交点情况，分情况讨论函数为一次函数和二次函数的时候，按照图像的性质以及与坐标轴交点的情况即可求出a 值．（2）①根据A 和B 的坐标点即可求出抛物线的解析式，即可求出顶点坐标P ，从而求出PH 长度，再利用A 和B 的坐标点即可求出BC 的直线解析式，结合F Px x =即可求出F 点坐标，从而求出PF 长度，最后利用面积法即可求出PBC 的面积．②观察图形，用m 值表示出点P 坐标，再根据平行线分线段成比例求出OD 长度，利用割补法表示出1S 和2S ，将二者相减转化成关于m 的二次函数的顶点式，利用m 取值范围即可求出12S S −的最小值．【详解】（1）解：函数的图象与坐标轴有两个公共点，()()2210a x a xb ∴−+++=， 4a b =，()()22104a a x a x ∴−+++=，当函数为一次函数时，20a −=，2a ∴=．当函数为二次函数时，()()22104a a x a x −+++=，若函数的图象与坐标轴有两个公共点，即与x 轴，y 轴分别只有一个交点时，()()2241424104a b ac a a a ∴∆=−=+−−⋅=+=，14a ∴=−． 当函数为二次函数时，函数的图象与坐标轴有两个公共点， 即其中一点经过原点， 0b ∴=，4a b =，0a ∴=．综上所述，2a =或0．故答案为：0或2或14−． （2）解：①如图所示，设直线l 与BC 交于点F ，直线l 与AB 交于点H ．依题意得：2102028a b a b +=⎧⎨+=⎩，解得：18a b =⎧⎨=⎩∴抛物线的解析式为：2228(1)9y x x x =−++=−−+．点P 为抛物线顶点时，(1,9)P ，(0,8)C ，9PH ∴=，1P x =，由()4,0B ，()0,8C 得直线BC 的解析式为28y x =−+， F 在直线BC 上，且在直线l 上，则F 的横坐标等于P 的横坐标，()1,6F ∴，6FH ∴=，1OH =，963PF PH FH ∴=−=−=，413BH OB OH =−=−=1111S S S 313362222PBC PFC PFB P x OH HB PF ∴=+=⋅+⋅=⨯⨯+⨯⨯=．故答案为：6．②12S S −存在最大值，理由如下：如图，设直线x m =交x 轴于H ．由①得：4OB =，2AO =，6AB =，8OC =，2AH m =+，()2,28P m m m −++228PH m m ∴=−++， OD x ⊥，PH AB ⊥，OD PH ∴∥，AO OD AH PH ∴=， 即22228OD m m m =+−++，82OD m ∴=−1S S S S PAB AOD EDOB=−−四边形，2S S S OBC EDOB =−四边形， ()()221262828248S S S S S 38222PAB AOD OBC m m m m m −++−⨯∴−=−−=−−=−+，212416S S 333m ⎛⎫∴−=−−+ ⎪⎝⎭， 30−<Q ，04m <<，∴当43m =时，12S S −有最大值，最大值为163． 故答案为：163．【点睛】本题考查了二次函数的综合应用，涉及到函数与坐标轴交点问题，二次函数与面积问题，平行线分线段成比例，解题的关键在于分情况讨论函数与坐标轴交点问题，以及二次函数最值问题． (1)求抛物线的解析式；(2)抛物线上是否存在点D ，使得DOB OBC ∠=∠？若存在，求出所有点在，请说明理由；(3)如图2，点E 是点B 关于抛物线对称轴的对称点，点F 是直线OB EF 与直线OB 交于点G ．设BFG 和BEG 的面积分别为1S 和2S ，求【答案】(1)24y x x =− (2)131339⎛⎫ ⎪⎝⎭，或()721，(3)2524【分析】（1）先求得点()55B ，，再利用待定系数法即可求解；（2）分点D 在直线OB 下方、上方两种情况，分别求解即可；（3）如图，分别过点E ，F 作y 轴的平行线，交直线OB 于点M ，N ，则()112B G S FN x x =−，()212B G S EM x x =−，设()24F m m m −，，可表达12S S ，再利用二次函数的性质可得出结论．【详解】（1）解：∵直线y x =经过点()5B t ，， ∴5t =，∴点()55B ，，∵抛物线2y ax bx c =++经过点()40A ，和点()55B ，以及原点，∴164025550a b c a b c c ++=⎧⎪++=⎨⎪=⎩，解得140a b c =⎧⎪=−⎨⎪=⎩，∴抛物线的解析式为24y x x =−；（2）解：∵抛物线()22424y x x x =−=−−， ∴顶点C 的坐标为()24−，，设直线BC 的解析式为：1y kx b =+，则将()55B ，，()24C −，代入1y kx b =+得，115524k b k b +=⎧⎨+=−⎩，解得310k b =⎧⎨=−⎩，∴直线BC 的解析式为：310y x =−．①当点D 在直线OB 的下方时，过点B 作BF x ⊥轴，交x 轴于点F ，延长OD ，交BF 于G ，设BC 交x 轴于点E ，如图，∵()55B ，，∴OF BF =，即45BOF OBF ∠=∠=︒，90OFG BFE ∠=∠=︒，∵DOB OBC ∠=∠，∴GOF EBF ∠∠=，∴()ASA OFG BFE △≌△，∴EF GF =．在310y x =−中，当0y =时，3100x −=，得：103x =， ∴1003E ⎛⎫ ⎪⎝⎭，， 则105533GF EF OF OE ==−=−=， ∴553G ⎛⎫ ⎪⎝⎭，，同理求得直线OG 的解析式为：13y x =， 联立：2134y x y x x ⎧=⎪⎨⎪=−⎩，解得133139x y ⎧=⎪⎪⎨⎪=⎪⎩或00x y =⎧⎨=⎩（舍去）， ∴131339D ⎛⎫ ⎪⎝⎭，；②当点D 在直线OB 的上方时，∵DOB OBC ∠=∠，∴∥OD BC ，∵直线BC 的解析式为：310y x =−，∴直线OD 的解析式为：3y x =，联立：234y x y x x =⎧⎨=−⎩，解得：721x y =⎧⎨=⎩或00x y =⎧⎨=⎩（舍去），∴()721 D，．综上，当点D的坐标为131339⎛⎫⎪⎝⎭，或()721，时，使得DOB OBC∠=∠；（3）解：∵点()55B，与点E关于对称轴直线2x=对称，∴()15E−，，如图，分别过点E，F作y轴的平行线，交直线OB于点M，N，∴()11M−−，，6EM=，设()24F m m m−，，则()N m m，，∴()2245FN m m m m m =−−=−+，∵()112B GS FN x x=−，()212B GS EM x x=−，∴()222125115255666224S FN m mm m mS EM−+⎛⎫===−−=−−+⎪⎝⎭，∴当52m=时，12SS的最大值为2524．【点睛】本题属于二次函数综合题，主要考查二次函数的性质，二次函数图象上点的坐标特征，三角形的面积和全等三角形的判定及性质，解题的关键正确表达两个三角形面积的比．。

题型六 二次函数与几何图形综合题类型一 二次函数与图形判定1．(2017·某某)在同一直角坐标系中，抛物线C 1：y ＝ax 2－2x －3与抛物线C 2：y ＝x 2＋mx ＋n 关于y 轴对称，C 2与x 轴交于A 、B 两点，其中点A 在点B 的左侧．(1)求抛物线C 1，C 2的函数表达式； (2)求A 、B 两点的坐标；(3)在抛物线C 1上是否存在一点P ，在抛物线C 2上是否存在一点Q ，使得以AB 为边，且以A 、B 、P 、Q 四点为顶点的四边形是平行四边形？若存在，求出P 、Q 两点的坐标；若不存在，请说明理由.2．(2017·随州)在平面直角坐标系中，我们定义直线y ＝ax －a 为抛物线y ＝ax 2＋bx ＋c(a 、b 、c 为常数，a ≠0)的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y 轴上的三角形为其“梦想三角形”．已知抛物线y ＝－233x 2－433x ＋23与其“梦想直线”交于A 、B 两点(点A 在点B 的左侧)，与x轴负半轴交于点C.(1)填空：该抛物线的“梦想直线”的解析式为__________，点A的坐标为__________，点B的坐标为__________；(2)如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点N的坐标；(3)当点E在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F，使得以点A、C、E、F为顶点的四边形为平行四边形？若存在，请直接写出点E、F的坐标；若不存在，请说明理由．(2017·某某模拟)已知：如图，抛物线y＝ax2－2ax＋c(a≠0)与y轴交于点C(0，4)，与x轴交于点A、B，点A的坐标为(4，0)．(1)求该抛物线的解析式；(2)点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ.当△CQE的面积最大时，求点Q的坐标；(3)若平行于x 轴的动直线l 与该抛物线交于点P ，与直线AC 交于点F ，点D 的坐标为(2，0)．问：是否存在这样的直线l ，使得△ODF 是等腰三角形？若存在，请求出点P 的坐标；若不存在，请说明理由.4．(2016·某某)如图①，直线y ＝－43x ＋n 交x 轴于点A ，交y 轴于点C(0，4)，抛物线y ＝23x 2＋bx ＋c 经过点A ，交y 轴于点B(0，－2)．点P 为抛物线上一个动点，过点P 作x轴的垂线PD ，过点B 作BD⊥PD 于点D ，连接PB ，设点P 的横坐标为m.(1)求抛物线的解析式；(2)当△BDP 为等腰直角三角形时，求线段PD 的长；(3)如图②，将△BDP 绕点B 逆时针旋转，得到△BD′P′，且旋转角∠PBP′＝∠OAC，当点P 的对应点P′落在坐标轴上时，请直接写出点P 的坐标.类型二 二次函数与图形面积1．(2017·某某)如图，在平面直角坐标系中，直线y ＝12x ＋2与x 轴交于点A ，与y 轴交于点C ，抛物线y ＝－12x 2＋bx ＋c 经过A 、C 两点，与x 轴的另一交点为点B.(1)求抛物线的函数表达式；(2)点D 为直线AC 上方抛物线上一动点；①连接BC 、CD ，设直线BD 交线段AC 于点E ，△CDE 的面积为S 1，△BCE 的面积为S 2，求S 1S 2的最大值； ②过点D 作DF⊥AC，垂足为点F ，连接CD ，是否存在点D ，使得△CDF 中的某个角恰好等于∠BAC 的2倍？若存在，求点D 的横坐标；若不存在，请说明理由．2．(2017·某某)如图甲，直线y＝－x＋3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y＝x2＋bx＋c与x轴的另一个交点为A，顶点为P.(1)求该抛物线的解析式；(2)在该抛物线的对称轴上是否存在点M，使以C，P，M为顶点的三角形为等腰三角形？若存在，请直接写出所有符合条件的点M的坐标；若不存在，请说明理由；(3)当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值(图乙、丙供画图探究).3．(2017·某某模拟)如图，抛物线y＝ax2＋bx－3与x轴交于点A(1，0)和点B，与y 轴交于点C，且其对称轴l为x＝－1，点P是抛物线上B，C之间的一个动点(点P不与点B，C重合)．(1)直接写出抛物线的解析式；(2)小唐探究点P的位置时发现：当动点N在对称轴l上时，存在PB⊥NB，且PB＝NB的关系，请求出点P的坐标；(3)是否存在点P使得四边形PBAC的面积最大？若存在，请求出四边形PBAC面积的最大值；若不存在，请说明理由.4．(2017·某某模拟)如图①，已知抛物线y＝ax2＋bx－3的对称轴为x＝1，与x轴分别交于A、B两点，与y轴交于点C，一次函数y＝x＋1经过A，且与y轴交于点D.(1)求该抛物线的解析式．(2)如图②，点P为抛物线B、C两点间部分上的任意一点(不含B，C两点)，设点P的横坐标为t，设四边形DCPB的面积为S，求出S与t的函数关系式，并确定t为何值时，S取最大值？最大值是多少？(3)如图③，将△ODB沿直线y＝x＋1平移得到△O′D′B′，设O′B′与抛物线交于点E，连接ED′，若ED′恰好将△O′D′B′的面积分为1∶2两部分，请直接写出此时平移的距离．类型三二次函数与线段问题1．(2017·某某)如图，已知抛物线y＝ax2－23ax－9a与坐标轴交于A，B，C三点，其中C(0，3)，∠BAC的平分线AE交y轴于点D，交BC于点E，过点D的直线l与射线AC，AB分别交于点M，N.(1)直接写出a的值、点A的坐标及抛物线的对称轴；(2)点P为抛物线的对称轴上一动点，若△PAD为等腰三角形，求出点P的坐标；(3)证明：当直线l绕点D旋转时，1AM ＋1AN均为定值，并求出该定值．2．(2017·某某模拟)如图①，直线y ＝34x ＋m 与x 轴、y 轴分别交于点A 和点B(0，－1)，抛物线y ＝12x 2＋bx ＋c 经过点B ，点C 的横坐标为4.(1)请直接写出抛物线的解析式；(2)如图②，点D 在抛物线上，DE ∥y 轴交直线AB 于点E ，且四边形DFEG 为矩形，设点D 的横坐标为x(0＜x ＜4)，矩形DFEG 的周长为l ，求l 与x 的函数关系式以及l 的最大值；(3)将△AOB 绕平面内某点M 旋转90°或180°，得到△A 1O 1B 1，点A 、O 、B 的对应点分别是点A 1、O 1、B 1.若△A 1O 1B 1的两个顶点恰好落在抛物线上，那么我们就称这样的点为“落点”，请直接写出“落点”的个数和旋转180°时点A 1的横坐标.3．(2017·某某)已知点A(－1，1)，B(4，6)在抛物线y＝ax2＋bx上．(1)求抛物线的解析式；(2)如图①，点F的坐标为(0，m)(m＞2)，直线AF交抛物线于另一点G，过点G作x轴的垂线，，连接FH、AE，求证：FH∥AE；(3)如图②，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒2个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM＝2PM，直接写出t的值.类型四二次函数与三角形相似1．(2016·某某)如图，已知抛物线经过原点O，顶点为A(1，1)，且与直线y＝x－2交于B，C两点．(1)求抛物线的解析式及点C的坐标；(2)求证：△ABC是直角三角形；(3)若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由.2．(2017·某某模拟)如图，抛物线y＝ax2＋bx＋1与直线y＝－ax＋c相交于坐标轴上点A(－3，0)，C(0，1)两点．(1)直线的表达式为__________；抛物线的表达式为__________；(2)D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交直线AC于点F，求线段DF长度的最大值，并求此时点D的坐标；(3)P为抛物线上一动点，且P在第四象限内，过点P作PN垂直x轴于点N，使得以P、A、N为顶点的三角形与△ACO相似，请直接写出点P的坐标.3．如图①，二次函数y ＝ax 2＋bx ＋33经过A(3，0)，G(－1，0)两点． (1)求这个二次函数的解析式；(2)若点M 是抛物线在第一象限图象上的一点，求△ABM 面积的最大值；(3)抛物线的对称轴交x 轴于点P ，过点E(0，233)作x 轴的平行线，交AB 于点F ，是否存在着点Q ，使得△FEQ∽△BEP？若存在，请直接写出点Q 的坐标；若不存在，请说明理由.4．(2017·某某)抛物线y ＝ax 2＋bx ＋3经过点A(1，0)和点B(5，0)． (1)求该抛物线所对应的函数解析式；(2)该抛物线与直线y＝错误!x＋3相交于C、D两点，点P是抛物线上的动点且位于x 轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N.①连接PC、PD，如图①，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；②连接PB，过点C作CQ⊥PM，垂足为点Q，如图②，是否存在点P，使得△Q与△PBM 相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由.题型六第23题二次函数与几何图形综合题类型一二次函数与图形判定1．解：(1)∵C1、C2关于y轴对称，∴C1与C2的交点一定在y轴上，且C1与C2的形状、大小均相同，∴a＝1，n＝－3，∴C1的对称轴为x＝1，∴C2的对称轴为x＝－1，∴m＝2，∴C1的函数表示式为y＝x2－2x－3，C2的函数表达式为y＝x2＋2x－3；(2)在C2的函数表达式为y＝x2＋2x－3中，令y＝0可得x2＋2x－3＝0，解得x＝－3或x＝1，∴A(－3，0)，B(1，0)；(3)存在．设P(a ，b)，则Q(a ＋4，b)或(a －4，b)， ①当Q(a ＋4，b)时，得：a 2－2a －3＝(a ＋4)2＋2(a ＋4)－3， 解得a ＝－2，∴b ＝a 2－2a －3＝4＋4－3＝5， ∴P 1(－2，5)，Q 1(2，5)． ②当Q(a －4，b)时，得：a 2－2a －3＝(a －4)2＋2(a －4)－3， 解得a ＝2.∴b ＝4－4－3＝－3， ∴P 2(2，－3)，Q 2(－2，－3)．综上所述，所求点的坐标为P 1(－2，5)，Q 1(2，5)； P 2(2，－3)，Q 2(－2，－3). 2．解：(1)∵抛物线y ＝－233x 2－433x ＋23， ∴其梦想直线的解析式为y ＝－233x ＋233，联立梦想直线与抛物线解析式可得⎩⎪⎨⎪⎧y ＝－233x ＋233y ＝－233x 2－433x ＋23，解得⎩⎨⎧x ＝－2y ＝23或⎩⎪⎨⎪⎧x ＝1y ＝0，∴A(－2，23)，B(1，0)；(2)当点N 在y 轴上时，△AMN 为梦想三角形， 如解图①，过A 作AD ⊥y 轴于点D ，则AD ＝2，在y ＝－233x 2－433x ＋23中，令y ＝0可求得x ＝－3或x ＝1，∴C(－3，0)，且A(－2，23)， ∴AC ＝（－2＋3）2＋（23）2＝13， 由翻折的性质可知AN ＝AC ＝13，在Rt △AND 中，由勾股定理可得DN ＝AN 2－AD 2＝13－4＝3， ∵OD ＝23，∴ON ＝23－3或ON ＝23＋3，当ON ＝23＋3时，则MN ＞OD ＞CM ，与MN ＝CM 矛盾，不合题意， ∴N 点坐标为(0，23－3)；当M 点在y 轴上时，则M 与O 重合，过N 作NP ⊥x 轴于点P ，如解图②，在Rt △AMD 中，AD ＝2，OD ＝23，∴tan ∠DAM ＝MDAD ＝3，∴∠DAM ＝60°，∵AD ∥x 轴，∴∠AMC ＝∠DAM ＝60°， 又由折叠可知∠NMA ＝∠AMC ＝60°， ∴∠NMP ＝60°，且MN ＝CM ＝3， ∴MP ＝12MN ＝32，NP ＝32MN ＝332，∴此时N 点坐标为(32，332)；综上可知N 点坐标为(0，23－3)或(32，332)；(3)①当AC 为平行四边形的边时，如解图③，过F 作对称轴的垂线FH ，过A 作AK ⊥x 轴于点K ，则有AC ∥EF 且AC ＝EF ，∴∠ACK ＝∠EFH ， 在△ACK 和△EFH 中，⎩⎪⎨⎪⎧∠ACK ＝∠EFH ∠AKC ＝∠EHF AC ＝EF，∴△ACK ≌△EFH(AAS )， ∴FH ＝CK ＝1，HE ＝AK ＝23，∵抛物线对称轴为x ＝－1，∴F 点的横坐标为0或－2，∵点F 在直线AB 上，∴当F 点横坐标为0时，则F(0，233)，此时点E 在直线AB 下方，∴E 到x 轴的距离为EH －OF ＝23－233＝433，即E 点纵坐标为－433，∴E(－1，－433)； 当F 点的横坐标为－2时，则F 与A 重合，不合题意，舍去； ②当AC 为平行四边形的对角线时， ∵C(－3，0)，且A(－2，23)， ∴线段AC 的中点坐标为(－52，3)，设E(－1，t)，F(x ，y)，则x －1＝2×(－52)，y ＋t ＝23，∴x ＝－4，y ＝23－t ，代入直线AB 解析式可得23－t ＝－233×(－4)＋233，解得t ＝－433，∴E(－1，－433)，F(－4，1033)；综上可知存在满足条件的点F ，此时E(－1，－433)、F(0，233)或E(－1，－433)、F(－4，1033).3．解：(1)由题意，得⎩⎪⎨⎪⎧0＝16a －8a ＋c 4＝c ，解得⎩⎪⎨⎪⎧a ＝－12c ＝4， ∴所求抛物线的解析式为y ＝－12x 2＋x ＋4；(2) 设点Q 的坐标为(m ，0)，如解图①，过点E 作EG ⊥x 轴于点G. 由－12x 2＋x ＋4＝0，得x 1＝－2，x 2＝4，∴点B 的坐标为(－2，0)，∴AB ＝6，BQ ＝m ＋2，∵QE ∥AC ，∴△BQE ∽△BAC ，∴EG CO ＝BQ BA ，即EG 4＝m ＋26，∴EG ＝2m ＋43，∴S △CQE ＝S △CBQ －S △EBQ ＝12BQ·CO－12BQ·EG＝12(m ＋2)(4－2m ＋43)＝－13m 2＋23m ＋83＝－13(m－1)2＋3，又∵－2≤m ≤4，∴当m ＝1时，S △CQE 有最大值3，此时Q(1，0)；图①图②(3)存在．在△ODF 中． (ⅰ)若DO ＝DF ，∵A(4，0)，D(2，0)，∴AD ＝OD ＝DF ＝2， 又∵在Rt △AOC 中，OA ＝OC ＝4，∴∠OAC ＝45°， ∴∠DFA ＝∠OAC ＝45°，∴∠ADF ＝90°，此时，点F 的坐标为(2，2)， 由－12x 2＋x ＋4＝2，得x 1＝1＋5，x 2＝1－5，此时，点P 的坐标为P(1＋5，2)或P(1－5，2)； (ⅱ)若FO ＝FD ，如解图②，过点F 作FM ⊥x 轴于点M ， 由等腰三角形的性质得：OM ＝MD ＝1，∴AM ＝3， ∴在等腰直角△AMF 中，MF ＝AM ＝3，∴F(1，3)， 由－12x 2＋x ＋4＝3，得x 1＝1＋3，x 2＝1－3，此时，点P 的坐标为：P(1＋3，3)或P(1－3，3)； (ⅲ)若OD ＝OF ，∵OA ＝OC ＝4，且∠AOC ＝90°，∴AC ＝42，∴点O 到AC 的距离为22，而OF ＝OD ＝2＜22，与OF ≥22矛盾， ∴AC 上不存在点使得OF ＝OD ＝2，此时，不存在这样的直线l ，使得△ODF 是等腰三角形． 综上所述，存在这样的直线l ，使得△ODF 是等腰三角形．所求点P 的坐标为(1＋5，2)或(1－5，2)或(1＋3，3)或(1－3，3). 4．解：(1)∵点C(0，4)在直线y ＝－43x ＋n 上，∴n ＝4，∴y ＝－43x ＋4，令y ＝0，解得x ＝3，∴A(3，0)，∵抛物线y ＝23x 2＋bx ＋c 经过点A ，交y 轴于点B(0，－2)，∴c ＝－2，6＋3b －2＝0，解得b ＝－43，∴抛物线的解析式为y ＝23x 2－43x －2；(2)∵点P 的横坐标为m ，且点P 在抛物线上， ∴P(m ，23m 2－43m －2)，∵PD ⊥x 轴，BD ⊥PD ，∴点D 坐标为(m ，－2)， ∴|BD|＝|m|，|PD|＝|23m 2－43m －2＋2|，当△BDP 为等腰直角三角形时，PD ＝BD ， ∴|m|＝|23m 2－43m －2＋2|＝|23m 2－43m|.∴m 2＝(23m 2－43m)2，解得：m 1＝0(舍去)，m 2＝72，m 3＝12，∴当△BDP 为等腰直角三角形时，线段PD 的长为72或12；(3)∵∠PBP′＝∠OAC ，OA ＝3，OC ＝4，∴AC ＝5， ∴sin ∠PBP ′＝45，cos ∠PBP ′＝35，①当点P′落在x 轴上时，如解图①，过点D′作D′N⊥x 轴，垂足为N ，交BD 于点M ，∠DBD ′＝∠ND′P′＝∠PBP′，由旋转知，P ′D ′＝PD ＝23m 2－43m ，在Rt △P ′D ′N 中，cos ∠ND ′P ′＝ND′P′D′＝cos ∠PBP ′＝35，∴ND ′＝35(23m 2－43m)，在Rt △BD ′M 中，BD ′＝－m ，sin ∠DBD ′＝D′M BD′＝sin ∠PBP ′＝45，∴D ′M ＝－45m ，∴ND ′－MD′＝2，∴35(23m 2－43m)－(－45m)＝2， 解得m ＝5(舍去)或m ＝－5，如解图②， 同①的方法得，ND ′＝35(23m 2－43m)，MD ′＝45m ，ND ′＋MD′＝2， ∴35(23m 2－43m)＋45m ＝2， ∴m ＝5或m ＝－5(舍去)，∴P(－5，45＋43)或P(5，－45＋43)，②当点P′落在y 轴上时，如解图③，过点D′作D′M⊥x 轴，交BD 于M ，过点P′作P′N⊥y 轴，交MD′的延长线于点N ， ∴∠DBD ′＝∠ND′P′＝∠PBP′，同①的方法得：P′N＝45(23m 2－43m)，BM ＝35m ，∵P ′N ＝BM ，∴45(23m 2－43m)＝35m ， 解得m ＝258或m ＝0(舍去)，∴P(258，1132)，∴P(－5，45＋43)或P(5，－45＋43)或P(258，1132).类型二 二次函数与图形面积1．解：(1)根据题意得A(－4，0)，C(0，2)， ∵抛物线y ＝－12x 2＋bx ＋c 经过A 、C 两点，∴⎩⎪⎨⎪⎧0＝－12×16－4b ＋c 2＝c ，解得⎩⎪⎨⎪⎧b ＝－32c ＝2， ∴y ＝－12x 2－32x ＋2；(2)①令y ＝0，∴－12x 2－32x ＋2＝0，解得x 1＝－4，x 2＝1，∴B(1，0)，如解图①，过D 作DM ∥y 轴交AC 于M ，过B 作BN ⊥x 轴交AC 于N ， ∴DM ∥BN ，∴△DME ∽△BNE ，∴S 1S 2＝DE BE ＝DMBN ，设D(a ，－12a 2－32a ＋2)，∴M(a ，12a ＋2)，∵B(1，0)，∴N(1，52)，∴S 1S 2＝DMBN ＝－12a 2－2a 52＝－15(a ＋2)2＋45； ∴当a ＝－2时，S 1S 2有最大值，最大值是45；②∵A(－4，0)，B(1，0)，C(0，2)， ∴AC ＝25，BC ＝5，AB ＝5， ∵AC 2＋BC 2＝AB 2，∴△ABC 是以∠ACB 为直角的直角三角形，取AB 的中点P ，∴P(－32，0)，∴PA ＝PC ＝PB ＝52，∴∠CPO ＝2∠BAC ，∴tan ∠CPO ＝tan (2∠BAC)＝43，如解图②，过D 作x 轴的平行线交y 轴于R ，交AC 的延长线于G ， 情况一：∠DCF ＝2∠BAC ＝∠DGC ＋∠CDG ，∴∠CDG ＝∠BAC ， ∴tan ∠CDG ＝tan ∠BAC ＝12，即RC DR ＝12，令D(a ，－12a 2－32a ＋2)，∴DR ＝－a ，RC ＝－12a 2－32a ，∴－12a 2－32a －a ＝12，解得a 1＝0(舍去)，a 2＝－2， ∴x D ＝－2，情况二：∠FDC ＝2∠BAC ， ∴tan ∠FDC ＝43，设FC ＝4k ，∴DF ＝3k ，DC ＝5k ， ∵tan ∠DGC ＝3k FG ＝12，∴FG ＝6k ，∴CG ＝2k ，DG ＝35k ，∴RC ＝255k ，RG ＝455k ， DR ＝35k －455k ＝1155k ，∴DR RC ＝1155k 255k ＝－a －12a 2－32a ，解得a 1＝0(舍去)，a 2＝－2911， ∴点D 的横坐标为－2或－2911.2．解：(1)∵直线y ＝－x ＋3与x 轴、y 轴分别交于点B 、点C ， ∴B(3，0)，C(0，3)，把B 、C 坐标代入抛物线解析式可得⎩⎪⎨⎪⎧9＋3b ＋c ＝0c ＝3，解得⎩⎪⎨⎪⎧b ＝－4c ＝3，∴抛物线的解析式为y ＝x 2－4x ＋3； (2)∵y ＝x 2－4x ＋3＝(x －2)2－1， ∴抛物线对称轴为x ＝2，P(2，－1)， 设M(2，t)，且C(0，3)，∴MC ＝22＋（t －3）2＝t 2－6t ＋13，MP ＝|t ＋1|，PC ＝22＋（－1－3）2＝25， ∵△CPM 为等腰三角形，∴有MC ＝MP 、MC ＝PC 和MP ＝PC 三种情况，①当MC ＝MP 时，则有t 2－6t ＋13＝|t ＋1|，解得t ＝32，此时M(2，32)；②当MC ＝PC 时，则有t 2－6t ＋13＝25，解得t ＝－1(与P 点重合，舍去)或t ＝7，此时M(2，7)；③当MP ＝PC 时，则有|t ＋1|＝25，解得t ＝－1＋25或t ＝－1－25，此时M(2，－1＋25)或(2，－1－25)；综上可知存在满足条件的点M ，其坐标为(2，32)或(2，7)或(2，－1＋25)或(2，－1－25)；(3)如解图，在0＜x ＜3对应的抛物线上任取一点E ，过E 作EF ⊥x 轴，交BC 于点F ，交x 轴于点D ，设E(x ，x 2－4x ＋3)，则F(x ，－x ＋3)， ∵0＜x ＜3，∴EF ＝－x ＋3－(x 2－4x ＋3)＝－x 2＋3x ，∴S △CBE ＝S △EFC ＋S △EFB ＝12EF·OD＋12EF·BD＝12EF·OB＝12×3(－x 2＋3x)＝－32(x －32)2＋278，∴当x ＝32时，△CBE 的面积最大，此时E 点坐标为(32，－34)，即当E 点坐标为(32，－34)时，△CBE 的面积最大.3．解：(1)∵A(1，0)，对称轴l 为x ＝－1，∴B(－3，0)，∴⎩⎪⎨⎪⎧a ＋b －3＝09a －3b －3＝0，解得⎩⎪⎨⎪⎧a ＝1b ＝2， ∴抛物线的解析式为y ＝x 2＋2x －3； (2)如解图①，过点P 作PM ⊥x 轴于点M ，设抛物线对称轴l 交x 轴于点Q. ∵PB ⊥NB ，∴∠PBN ＝90°， ∴∠PBM ＋∠NBQ ＝90°.∵∠PMB ＝90°，∴∠PBM ＋∠BPM ＝90°， ∴∠BPM ＝∠NBQ.又∵∠BMP ＝∠BQN ＝90°，PB ＝NB ，∴△BPM ≌△NBQ ，∴PM ＝BQ.∵抛物线y ＝x 2＋2x －3与x 轴交于点A(1，0)和点B ，且对称轴为x ＝－1， ∴点B 的坐标为(－3，0)，点Q 的坐标为(－1，0)， ∴BQ ＝2，∴PM ＝BQ ＝2.∵点P 是抛物线y ＝x 2＋2x －3上B 、C 之间的一个动点， ∴结合图象可知点P 的纵坐标为－2，将y ＝－2代入y ＝x 2＋2x －3，得－2＝x 2＋2x －3， 解得x 1＝－1－2，x 2＝－1＋2(舍去)， ∴此时点P 的坐标为(－1－2，－2)； (3) 存在．如解图②，连接AC ，PC.可设点P 的坐标为(x ，y)(－3＜x ＜0)，则y ＝x 2＋2x －3， ∵点A(1，0)，∴OA ＝1.∵点C 是抛物线与y 轴的交点，∴令x ＝0，得y ＝－3，即点C(0，－3)，∴OC ＝3. 由(2)可知S四边形PBAC＝S △BPM ＋S四边形PMOC＋S △AOC ＝12BM·PM＋12(PM ＋OC)·OM＋12OA·OC＝12(x＋3)(－y)＋12(－y ＋3)(－x)＋12×1×3＝－32y －32x ＋32，将y ＝x 2＋2x －3代入可得S 四边形PBAC ＝－32(x 2＋2x －3)－32x ＋32＝－32(x ＋32)2＋758.∵－32＜0，－3＜x ＜0，∴当x ＝－32时，S 四边形PBAC 有最大值758，此时，y ＝x 2＋2x －3＝－154.∴当点P 的坐标为(－32，－154)时，四边形PBAC 的面积最大，最大值为758.4．解：(1)把y ＝0代入直线的解析式得x ＋1＝0，解得x ＝－1，∴A(－1，0)． ∵抛物线的对称轴为x ＝1，∴B 的坐标为(3，0)． 将x ＝0代入抛物线的解析式得y ＝－3，∴C(0，－3)．设抛物线的解析式为y ＝a(x ＋1)(x －3)，将C(0，－3)代入得－3a ＝－3，解得a ＝1， ∴抛物线的解析式为y ＝(x ＋1)(x －3)＝x 2－2x －3； (2)如解图①，连接OP.将x ＝0代入直线AD 的解析式得y ＝1，∴OD ＝1. 由题意可知P(t ，t 2－2t －3)． ∵S 四边形DCPB ＝S △ODB ＋S △OBP ＋S △OCP ，∴S ＝12×3×1＋12×3×(－t 2＋2t ＋3)＋12×3×t ，整理得S ＝－32t 2＋92t ＋6，配方得：S ＝－32(t －32)2＋758，∴当t ＝32时，S 取得最大值，最大值为758；(3)如解图②，设点D′的坐标为(a ，a ＋1)，O ′(a ，a)．当△D′O′E 的面积∶△D′EB′的面积＝1∶2时，则O′E∶EB ′＝1∶2. ∵O ′B ′＝OB ＝3，∴O ′E ＝1， ∴E(a ＋1，a)．将点E 的坐标代入抛物线的解析式得(a ＋1)2－2(a ＋1)－3＝a ，整理得：a 2－a －4＝0，解得a ＝1＋172或a ＝1－172，∴O ′的坐标为(1＋172，1＋172)或(1－172，1－172)，∴OO ′＝2＋342或OO′＝34－22， ∴△DOB 平移的距离为2＋342或34－22， 当△D′O′E 的面积∶△D ′EB ′的面积＝2∶1时，则O′E∶EB ′＝2∶1. ∵O ′B ′＝OB ＝3，∴O ′E ＝2，∴E(a ＋2，a)．将点E 的坐标代入抛物线的解析式得：(a ＋2)2－2(a ＋2)－3＝a ，整理得：a 2＋a －3＝0，解得a ＝－1＋132或a ＝－1－132.∴O ′的坐标为(－1＋132，－1＋132)或(－1－132，－1－132)．∴OO′＝－2＋262或OO′＝2＋262.∴△DOB 平移的距离为－2＋262或2＋262.综上所述，当△D′O′B′沿DA 方向平移2＋342或2＋262单位长度，或沿AD 方向平移34－22或－2＋262个单位长度时，ED ′恰好将△O′D′B′的面积分为1∶2两部分. 类型三 二次函数与线段问题1．(1)解：∵C(0，3)，∴－9a ＝3，解得a ＝－13.令y ＝0，得ax 2－23ax －9a ＝0，∵a ≠0，∴x 2－23x －9＝0，解得x ＝－3或x ＝3 3. ∴点A 的坐标为(－3，0)，点B 的坐标为(33，0)，∴抛物线的对称轴为x ＝3； (2)解：∵OA ＝3，OC ＝3， ∴tan ∠CAO ＝3，∴∠CAO ＝60°. ∵AE 为∠BAC 的平分线，∴∠DAO ＝30°， ∴DO ＝33AO ＝1，∴点D 的坐标为(0，1)， 设点P 的坐标为(3，a)．∴AD 2＝4，AP 2＝12＋a 2，DP 2＝3＋(a －1)2. 当AD ＝PA 时，4＝12＋a 2，方程无解．当AD ＝DP 时，4＝3＋(a －1)2，解得a ＝0或a ＝2， ∴点P 的坐标为(3，0)或(3，2)．当AP ＝DP 时，12＋a 2＝3＋(a －1)2，解得a ＝－4. ∴点P 的坐标为(3，－4)．综上所述，点P 的坐标为(3，0)或(3，－4)或(3，2);(3)证明：设直线AC 的解析式为y ＝mx ＋3，将点A 的坐标代入得－3m ＋3＝0，解得m ＝3，∴直线AC 的解析式为y ＝3x ＋3. 设直线MN 的解析式为y ＝kx ＋1.把y ＝0代入y ＝kx ＋1，得kx ＋1＝0，解得：x ＝－1k ，∴点N 的坐标为(－1k ，0)，∴AN ＝－1k ＋3＝3k －1k.将y ＝3x ＋3与y ＝kx ＋1联立，解得x ＝2k －3，∴点M 的横坐标为2k －3.如解图，过点M 作MG ⊥x 轴，垂足为G.则AG ＝2k －3＋ 3.∵∠MAG ＝60°，∠AGM ＝90°， ∴AM ＝2AG ＝4k －3＋23＝23k －2k －3.∴1AM ＋1AN ＝k －323k －2＋k 3k －1＝k －323k －2＋2k 23k －2＝3k －323k －2＝3（3k －1）2（3k －1）＝32. 2．解：(1)∵直线l ：y ＝34x ＋m 经过点B(0，－1)，∴m ＝－1，∴直线l 的解析式为y ＝34x －1，∵直线l ：y ＝34x －1经过点C ，且点C 的横坐标为4，∴y ＝34×4－1＝2，∵抛物线y ＝12x 2＋bx ＋c 经过点C(4，2)和点B(0，－1)，∴⎩⎪⎨⎪⎧12×42＋4b ＋c ＝2c ＝－1，解得⎩⎪⎨⎪⎧b ＝－54c ＝－1， ∴抛物线的解析式为y ＝12x 2－54x －1；(2)令y ＝0，则34x －1＝0，解得x ＝43，∴点A 的坐标为(43，0)，∴OA ＝43，在Rt △OAB 中，OB ＝1，∴AB ＝OA 2＋OB 2＝（43）2＋12＝53， ∵DE ∥y 轴，∴∠ABO ＝∠DEF ，在矩形DFEG 中，EF ＝DE·cos ∠DEF ＝DE·OB AB ＝35DE ，DF ＝DE·sin ∠DEF ＝DE·OA AB ＝45DE ，∴l ＝2(DF ＋EF)＝2×(45＋35)DE ＝145DE ，∵点D 的横坐标为t(0＜t ＜4)， ∴D(t ，12t 2－54t －1)，E(t ，34t －1)，∴DE ＝(34t －1)－(12t 2－54t －1)＝－12t 2＋2t ，∴l ＝145×(－12t 2＋2t)＝－75t 2＋285t ，∵l ＝－75(t －2)2＋285，且－75＜0，∴当t ＝2时，l 有最大值285；(3)“落点”的个数有4个，如解图①，解图②，解图③，解图④所示．如解图③，设A 1的横坐标为m ，则O 1的横坐标为m ＋43，∴12m 2－54m －1＝12(m ＋43)2－54(m ＋43)－1， 解得m ＝712，如解图④，设A 1的横坐标为m ，则B 1的横坐标为m ＋43，B 1的纵坐标比A 1的纵坐标大1，∴12m 2－54m －1＋1＝12(m ＋43)2－54(m ＋43)－1，解得m ＝43， ∴旋转180°时点A 1的横坐标为712或43.3．(1)解：将点A(－1，1)，B(4，6)代入y ＝ax 2＋bx 中， 得⎩⎪⎨⎪⎧a －b ＝116a ＋4b ＝6，解得⎩⎪⎨⎪⎧a ＝12b ＝－12， ∴抛物线的解析式为y ＝12x 2－12x ；(2)证明：设直线AF 的解析式为y ＝kx ＋m ， 将点A(－1，1)代入y ＝kx ＋m 中，即－k ＋m ＝1， ∴k ＝m －1，∴直线AF 的解析式为y ＝(m －1)x ＋m. 联立直线AF 和抛物线解析式成方程组，⎩⎪⎨⎪⎧y ＝（m －1）x ＋m y ＝12x 2－12x ，解得⎩⎪⎨⎪⎧x 1＝－1y 1＝1，⎩⎪⎨⎪⎧x 2＝2my 2＝2m 2－m ， ∴点G 的坐标为(2m ，2m 2－m)． ∵GH ⊥x 轴，∴点H 的坐标为(2m ，0)． ∵抛物线的解析式为y ＝12x 2－12x ＝12x(x －1)，∴点E 的坐标为(1，0)．设直线AE 的解析式为y ＝k 1x ＋b 1，将A(－1，1)，E(1，0)代入y ＝k 1x ＋b 1中，得⎩⎪⎨⎪⎧－k 1＋b 1＝1k 1＋b 1＝0，解得⎩⎪⎨⎪⎧k 1＝－12b 1＝12，∴直线AE 的解析式为y ＝－12x ＋12.设直线FH 的解析式为y ＝k 2x ＋b 2，将F(0，m)、H(2m ，0)代入y ＝k 2x ＋b 2中，得⎩⎪⎨⎪⎧b 2＝m 2mk 2＋b 2＝0，解得：⎩⎪⎨⎪⎧k 2＝－12b 2＝m， ∴直线FH 的解析式为y ＝－12x ＋m.∴FH ∥AE ；(3)解：设直线AB 的解析式为y ＝k 0x ＋b 0，将A(－1，1)，B(4，6)代入y ＝k 0x ＋b 0中，⎩⎪⎨⎪⎧－k 0＋b 0＝14k 0＋b 0＝6，解得⎩⎪⎨⎪⎧k 0＝1b 0＝2， ∴直线AB 的解析式为y ＝x ＋2.当运动时间为t 秒时，点P 的坐标为(t －2，t)，点Q 的坐标为(t ，0)．当点M 在线段PQ 上时，过点P 作PP′⊥x 轴于点P′，过点M 作MM′⊥x 轴于点M′，则△PQP′∽△MQM′，如解图所示．∵QM ＝2PM ， ∴QM′QP′＝MM′PP′＝23，∴QM ′＝43，MM ′＝23t ，∴点M 的坐标为(t －43，23t)，又∵点M 在抛物线y ＝12x 2－12x 上，∴23t ＝12(t －43)2－12(t －43)， 解得t ＝15±1136，当点M 在线段QP 的延长线上时， 同理可得出点M 的坐标为(t －4，2t)， ∵点M 在抛物线y ＝12x 2－12x 上，∴2t ＝12×(t －4)2－12(t －4)，解得t ＝13±892.综上所述：当运动时间为15－1136秒、15＋1136秒、13－892秒或13＋892秒时，QM ＝2PM.类型四 二次函数与三角形相似 1．(1)解：∵顶点坐标为(1，1)， ∴设抛物线解析式为y ＝a(x －1)2＋1，又∵抛物线过原点，∴0＝a(0－1)2＋1，解得a ＝－1， ∴抛物线的解析式为y ＝－(x －1)2＋1，即y ＝－x 2＋2x ，联立抛物线和直线解析式可得⎩⎪⎨⎪⎧y ＝－x 2＋2x y ＝x －2，解得⎩⎪⎨⎪⎧x ＝2y ＝0或⎩⎪⎨⎪⎧x ＝－1y ＝－3， ∴B(2，0)，C(－1，－3)；(2)证明：如解图，分别过A 、C 两点作x 轴的垂线，交x 轴于D 、E 两点， 则AD ＝OD ＝BD ＝1，BE ＝OB ＋OE ＝2＋1＝3，EC ＝3， ∴∠ABO ＝∠CBO ＝45°，即∠ABC ＝90°， ∴△ABC 是直角三角形；(3)解：假设存在满足条件的点N ，设N(x ，0)，则M(x ，－x 2＋2x)， ∴ON ＝|x|，MN ＝|－x 2＋2x|，由(2)在Rt △ABD 和Rt △CEB 中，可分别求得AB ＝2，BC ＝32， ∵MN ⊥x 轴于点N ∴∠MNO ＝∠ABC ＝90°，∴当△MNO 和△ABC 相似时有MN AB ＝ON BC 或MN BC ＝ONAB，①当MN AB ＝ON BC 时，则有|－x 2＋2x|2＝|x|32，即|x|×|－x ＋2|＝13|x|，∵当x ＝0时M 、O 、N 不能构成三角形， ∴x ≠0，∴|－x ＋2|＝13，即－x ＋2＝±13，解得x ＝53或x ＝73，此时N 点坐标为(53，0)或(73，0)，②当MN BC ＝ON AB 时，则有|－x 2＋2x|32＝|x|2，即|x|×|－x ＋2|＝3|x|，∴|－x ＋2|＝3，即－x ＋2＝±3，解得x ＝5或x ＝－1， 此时N 点坐标为(－1，0)或(5，0)，综上可知存在满足条件的N 点，其坐标为(53，0)或(73，0)或(－1，0)或(5，0).2．解：(1)把A 、C 两点坐标代入直线y ＝－ax ＋c 可得⎩⎪⎨⎪⎧3a ＋c ＝0c ＝1，解得⎩⎪⎨⎪⎧a ＝－13c ＝1， ∴直线的表达式为y ＝13x ＋1，把A 点坐标和a ＝－13代入抛物线解析式可得9×(－13)－3b ＋1＝0，解得b ＝－23，∴抛物线的表达式为y ＝－13x 2－23x ＋1；(2)∵点D 为抛物线在第二象限部分上的一点，∴可设D(t ，－13t 2－23t ＋1)，则F(t ，13t ＋1)，∴DF ＝－13t 2－23t ＋1－(13t ＋1)＝－13t 2－t ＝－13(t ＋32)2＋34.∵－13＜0，∴当t ＝－32时，DF 有最大值，最大值为34，此时D 点坐标为(－32，54)；(3)设P(m ，－13m 2－23m ＋1)，如解图，∵P 在第四象限，∴m ＞0，－13m 2－23m ＋1＜0，∴AN ＝m ＋3，PN ＝13m 2＋23m －1，∵∠AOC ＝∠ANP ＝90°，∴当以P 、A 、N 为顶点的三角形与△ACO 相似时有△AOC ∽△PNA 和△AOC ∽△ANP ，①当△AOC ∽△PNA 时，则有OC NA ＝AO PN ，即1m ＋3＝313m 2＋23m －1，解得m ＝－3或m ＝10，经检验当m ＝－3时，m ＋3＝0(舍去)， ∴m ＝10，此时P 点坐标为(10，－39)；②当△AOC ∽△ANP 时，则有OC NP ＝AO AN ，即113m 2＋23m －1＝3m ＋3，解得m ＝2或m ＝－3，经检验当m ＝－3时，m ＋3＝0(舍去)， ∴m ＝2，此时P 点坐标为(2，－53)；综上可知P 点坐标为(10，－39)或(2，－53).3．解：(1)将A 、G 点坐标代入函数解析式，得⎩⎨⎧9a ＋3b ＋33＝0，a －b ＋33＝0，解得⎩⎨⎧a ＝－3b ＝23，∴抛物线的解析式为y ＝－3x 2＋23x ＋33； (2)如解图①，作ME ∥y 轴交AB 于E 点， 当x ＝0时，y ＝33，即B 点坐标为(0，33)， 直线AB 的解析式为y ＝－3x ＋33，设M(n ，－3n 2＋23n ＋33)，E(n ，－3n ＋33)， ME ＝－3n 2＋23n ＋33－(－3n ＋33)＝－3n 2＋33n ， S △ABM ＝12ME·AO＝12(－3n 2＋33n)×3＝－332(n －32)2＋2738，当n ＝32时，△ABM 面积的最大值是2738；(3)存在；理由如下：OE ＝233，AP ＝2，OP ＝1，BE ＝33－233＝733，当y ＝233时，－3x ＋33＝233，解得x ＝73，即EF ＝73，将△BEP 绕点E 顺时针方向旋转90°，得到△B′EC(如解图②)， ∵OB ⊥EF ，∴点B′在直线EF 上，∵C 点横坐标绝对值等于EO 长度，C 点纵坐标绝对值等于EO －PO 长度， ∴C 点坐标为(－233，233－1)，如解图，过F 作FQ ∥B′C，交EC 于点Q ， 则△FEQ ∽△B′EC，由BE EF ＝B′E EF ＝CEEQ ＝3，可得Q 的坐标为(－23，－33)；根据对称性可得，Q 关于直线EF 的对称点Q′(－23，533)也符合条件.4．解：(1)∵抛物线y ＝ax 2＋bx ＋3经过点A(1，0)和点B(5，0)， ∴⎩⎪⎨⎪⎧a ＋b ＋3＝025a ＋5b ＋3＝0，解得⎩⎪⎨⎪⎧a ＝35b ＝－185， ∴该抛物线对应的函数解析式为y ＝35x 2－185x ＋3；(2)①∵点P 是抛物线上的动点且位于x 轴下方，∴可设P(t ，35t 2－185t ＋3)(1＜t ＜5)，∵直线PM ∥y 轴，分别与x 轴和直线CD 交于点M 、N ， ∴M(t ，0)，N(t ，35t ＋3)，∴PN ＝35t ＋3－(35t 2－185t ＋3)＝－35(t －72)2＋14720，联立直线CD 与抛物线解析式可得⎩⎪⎨⎪⎧y ＝35x ＋3y ＝35x 2－185x ＋3，解得⎩⎪⎨⎪⎧x ＝0y ＝3或⎩⎪⎨⎪⎧x ＝7y ＝365，∴C(0，3)，D(7，365)，分别过C 、D 作直线PN 的垂线，垂足分别为E 、F ，如解图①，则CE ＝t ，DF ＝7－t ，∴S △PCD ＝S △P ＋S △PDN ＝12PN·CE＋12PN·DF＝72PN ＝72[－35(t －72)2＋14720]＝－2110(t －72)2＋102940， ∴当t ＝72时，△PCD 的面积最大，最大值为102940；②存在．∵∠CQN ＝∠PMB ＝90°， ∴当△Q 与△PBM 相似时，有NQ CQ ＝PM BM 或NQ CQ ＝BMPM两种情况， ∵CQ ⊥PN ，垂足为Q ，∴Q(t ，3)，且C(0，3)，N(t ，35t ＋3)，∴CQ ＝t ，NQ ＝35t ＋3－3＝35t ，∴NQ CQ ＝35，∵P(t ，35t 2－185t ＋3)，M(t ，0)，B(5，0)，∴BM ＝5－t ，PM ＝0－(35t 2－185t ＋3)＝－35t 2＋185t －3，当NQ CQ ＝PM BM 时，则PM ＝35BM ，即－35t 2＋185t －3＝35(5－t)，解得t ＝2或t ＝5(舍去)，此时P(2，－95)；当NQ CQ ＝BM PM 时，则BM ＝35PM ，即5－t ＝35(－35t 2＋185t －3)，解得t ＝349或t ＝5(舍去)，此时P(349，－5527)；综上可知存在满足条件的点P ，其坐标为(2，－95)或(349，－5527).。

中考数学专题复习：二次函数综合题（面积问题）1．如图，一次函数y ＝kx +b 的图象与二次函数y ＝ax 2的图象交于点A （1，m ）和B （﹣2，4），与y 轴交于点C ．(1)求k ，b ，a 的值； (2)求△AOB 的面积．2． 如图，已知二次函数212y x bx c =-++的图象经过点A (2，0)，B (0，-6)两点．(1)求这个二次函数的解析式；(2)设该二次函数的对称轴与x 轴交于点C ，连接BA 、BC ，求△ABC 的面积．3．如图，在平面直角坐标系中，一次函数y ＝kx +b 的图象经过点A （0，﹣4）、B （2，0），交反比例函数y 6x=（x ＞0）的图象于点C ，点P 在反比例函数的图象上，横坐标为n （0＜n ＜3），PQ y ∥轴交直线AB 于点Q ，D 是y 轴上任意一点，连接PD 、QD ．(1)求一次函数的表达式和C点坐标；(2)求△DPQ面积的最大值．4．如图，抛物线2y x bx c=-++交x轴于A，B两点，交y轴于点C直线122y x=-+经过点B，C．(1)求抛物线的解析式；(2)点P是直线BC上方抛物线上一动点，设点P的横坐标为m．△求△PBC面积最大值和此时m的值；△Q是直线BC上一动点，是否存在点P，使以A、B、P、Q为顶点的四边形是平行四边形，若存在，直接写出点P的坐标．5．图1，抛物线2y x 2x 3=-++与x 轴交于A ，B 两点，与y 轴交于点C ．(1)求点A ，B ，C 的坐标．(2)P 为直线BC 上方抛物线上的一个动点，当PBC 的面积最大时，求点P 的坐标； (3)设M 为该抛物线的顶点，D 为抛物线的对称轴与x 轴的交点，如图2所示，在直线MD 上是否存在点N ，使点N 到直线MC 的距离等于点N 到点A 的距离？若存在，直接写出点N 的坐标；若不存在，请说明理由．6．如图，已知二次函数2y x bx c =-++的图像交x 轴于点()1,0A -，()5,0B ，交y 轴于点C ．(1)求这个二次函数的表达式；(2)如图1，点M 从点B 出发，BC 向点C 运动，点N 从点O 出发，以每秒1个单位长度的速度沿线段OB 向点B 运动，点M ，N 同时出发．设运动时间为t 秒（05t <<）．当t 为何值时，BMN △的面积最大？最大面积是多少？ (3)已知P 是抛物线上一点，在直线BC 上是否存在点Q ，使以A ，C ，P ，Q 为顶点的四边形是平行四边形？若存在，直接写出点Q 坐标；若不存在，请说明理由．7．如图，已知抛物线2342y ax x =++的对称轴是直线x =3，且与x 轴相交于A 、B 两点（B 点在A 点的右侧），与y 轴交于C 点．(1)A 点的坐标是_____________；B 点坐标是________________； (2)求直线BC 的解析式；(3)点P 是直线BC 上方的抛物线上的一动点（不与B 、C 重合），是否存在点P ，使△PBC 的面积最大．若存在，请求出△PBC 的最大面积，若不存在，试说明理由；(4)若点M 在x 轴上，点N 在抛物线上，以A 、C 、M 、N 为顶点的四边形是平行四边形时，请直接写出点M 点坐标．8．如图，抛物线()20y ax bx c a =++≠与y 轴交于点C （0，4），与x 轴交于点A 和点B ，其中点A 的坐标为（﹣2，0），抛物线的对称轴x ＝1与抛物线交于点D ，与直线BC 交于点E ．(1)求抛物线的解析式；(2)若点F 是直线BC 上方的抛物线上的一个动点，是否存在点F 使四边形ABFC 的面积最大，若存在，求出点F 的坐标和最大值；若不存在，请说明理由；(3)平行于DE 的一条动直线l 与直线BC 相交于点P ，与抛物线相交于点Q ，若以D 、E 、P 、Q 为顶点的四边形是平行四边形，求P 点的坐标．(4)探究对称轴上是否存在一点P ，使得以点P ，C ，A 为顶点的三角形是等腰三角形？若存在，请求出所有符合条件的P 点的坐标，若不存在，请说明理由．9．如图，在平面直角坐标系中，直线334y x =-+与x 轴交于点A ，与y 轴交于点C ．抛物线214y x bx c =-++经过点A 、C ．(1)求抛物线解析式及顶点M 坐标；(2)P 为抛物线第一象限内一点，使得PAC △面积最大，求PAC △面积的最大值及此时点P 的坐标；(3)当1m x m +≤≤时，（1）中二次函数有最大值为2-，求m 的值．10．如图，在平面直角坐标系中，二次函数2y ax x c =-+的图像与x 轴交于点A (2-，0)、B (4，0)，与y 轴交于点C ．(1)求a 和c 的值；(2)若点D （不与点C 重合）在该二次函数的图像上，且ABD ABC S S =△△，求点D 的坐标；(3)若点P 是该二次函数图像上位于x 轴上方的一点，且BPABPCS S=，直接写出点P 的坐标．11．如图，抛物线()214y x =--的图像与x 轴交于的A 、B 两点，与y 轴交于点D ，抛物线的顶点为C ．(1)求点A 、B 、C 坐标； (2)求ABC 的面积；(3)点P 是抛物线上一动点，当ABP △的面积为6时，求所有符合条件的点P 的坐标；12．如图，抛物线()20y ax bx c a =++≠经过点A (2，0)，B (-2，4)，(-4，0)，直线AB 与抛物线的对称轴交于点E ．(1)求抛物线的表达式；(2)点M 在直线AB 上方的抛物线上运动，当ΔABM 的面积最大时，求点M 的坐标； (3)若点F 为平面内的一点，且以点,,,B E C F 为顶点的四边形是平行四边形，请写出符合条件的点F 的坐标．13．如图，直线y=-x+4与x轴交于点C，与y轴交于点B，抛物线y=23x2+bx+c经过B、C两点．(1)求抛物线的解析式；(2)如图，点E是抛物线上的一动点（不与B，C两点重合），当S△BEC=14S△BOC时，求点E的坐标；(3)若点F是抛物线上的一动点，当S△BFC取值在什么范围时，对应的点F有且只有两个？14．如图，已知抛物线y＝ax2＋bx－8的图像与x轴交于A（2，0），B（﹣8，0）两点，与y轴交于点C（0，﹣8）．(1)求抛物线的解析式；(2)点F是直线BC下方抛物线上的一点，当△BCF的面积最大时，求出点F的坐标；(3)在（2）的条件下，是否存在这样的点Q（0，m），使得△BFQ为等腰三角形？如果有，请直接写出点Q 的坐标；如果没有，请说明理由．15．如图，已知抛物线2y ax bx c ++＝交x 轴于点A 、B ，交y 轴于点C （0，6），且顶点坐标为（4，﹣2）．直线x ＝m 分别交直线BC 和抛物线于点E 、P ．(1)求该抛物线的解析式及A 、B 两点坐标； (2)当0＜m ＜6时，求△BCP 面积的最大值； (3)当△BPE 是等腰三角形时，直接写出m 的值．16．已知二次函数242y ax x =++的图象经过点()3,4A -．(1)求a 的值；(2)直接写出函数y 随自变量的增大而减小的x 的取值范围．(3)设242y ax x =++的顶点为M ，与y 轴相交于C ，连结MC 、MA 、AC ，求AMC S △．17．如图，抛物线23y ax bx =++与x 轴交于点()3,0A ，与y 轴交于点B ，点C 在直线AB 上，过点C 作CD x ⊥轴于点()1,0D ，将ACD △沿CD 所在直线翻折，使点A 恰好落在抛物线上的点E 处．(1)求抛物线解析式；(2)连接BE ，求BCE 的面积；(3)拋物线上是否存在一点P ，使PEA BAE ∠=∠？若存在，求出P 点坐标；若不存在，请说明理由．18．在平面直角坐标系中，点O 为坐标原点，抛物线y =ax 2+bx +3交x 轴负半轴于点A ，交x 轴正半轴于点B ，交y 轴于点C ，且OA =OC =3OB ．(1)求这个抛物线的解析式；(2)如图1，点P 为第三象限抛物线上的点，设点P 的横坐标为t ，△P AC 面积S ，求S 与t 的函数解析式（直接写出自变量t 的取值范围）；(3)如图2，在（2）的条件下，Q 为CA 延长线上的一点，若P 到x 轴的距离为d ，△PQB 的面积为2d ，且△P AQ =△AQB ，求点P 的坐标．19．如图，已知抛物线2y x bx c =++经过点()30A -,和点()0,3C -．解答下列问题．(1)求抛物线的解析式；(2)抛物线的顶点为D ，对称轴与x 轴的交点为E ，求线段BD 的长；(3)点F 在抛物线上运动，是否存在点F 使FAB 的面积等于6？如果存在，求出点F 的坐标；如果不存在，说明理由．20．如图，抛物线23y ax bx =++经过点A （2，3），与x 轴负半轴交于点B ，与y 轴交于点C ，且3OC OB =．(1)求该抛物线的解析式；(2)点D 在y 轴上，且BDO BAC ∠=∠，求点D 的坐标；(3)点P 在直线AB 上方的抛物线上，当△P AB 的面积最大时，直接写出点P 的坐标．参考答案：1．(1)k =−1，a =1，b =2(2)S △AOB =32．(1)21462y x x =-+- (2)63．(1)一次函数的表达式：y =2x -4，点C （3，2）；(2)DPQ 面积的最大值是4．4．(1)2722y x x =-++(2)△最大值为8，m ＝2；△存在，⎝⎭或⎝⎭5．(1)A (﹣1，0)，B (3，0)，C (0，3) (2)31524P ⎛⎫ ⎪⎝⎭，(3)存在，(14N -+，或(14--，6．(1)245y x x =-++(2)当52t =时，BMN △的面积最大，最大面积是258(3)存在，Q 的坐标为()7,12-或()7,2-或()1,4或()2,37．(1)()-2,0，()8,0(2)直线BC 的解析式为142y x =-+ (3)存在点P ，使PBC ∆的面积最大，最大面积是16，理由见详解(4)满足条件的点M 的坐标为(8,0)-，(4,0)，(50)，(5，0)8．(1)y ＝﹣12x 2+x +4(2)存在，四边形ABFC 的面积最大为16，F （2，4）(3)P 点坐标为（3，1）或（，2）或（2(4)存在，P 点坐标为（1或（1，或（1，1）或（1，或（1，49．(1)211344y x x =-++，顶点M 的坐标为149,216⎛⎫ ⎪⎝⎭ (2)最大值为2，此时P 点坐标为52,2⎛⎫ ⎪⎝⎭(3)5-或510．(1)142a c ==-，4)或(14)或(2，-4)(3)(-6，20)11．(1)()1,0A -，()3,0B ，()1,4C -(2)8(3)()0,3-或()2,3-或()1或()112．(1)2142y x x =--+(2)（0，4）(3)（-5，1）或（1，7）或（-3，-1）13．(1)y ＝23-x 2+53x +4(2)E 1)，E 2)，E 34222，，E 44222， (3)当S △BFC ＞163时，对应的点F 有且只有两个．14．(1)抛物线解析式为y ＝122x +3x ﹣8；(2)点F 的坐标是F （﹣4，﹣12）；(3)存在，点Q 有坐标为（0，0，﹣0，﹣4）或（0，0）．15．(1)21462y x x =-+，点A （2，0），点B （6，0） (2)S △BCP 的最大值为272(3)当△BPE 是等腰三角形时，m 的值为2或416．(1)2242y x x =-++(2)1x >(3)617．(1)2y x 2x 3=-++(2)2(3)存在，()2,3或()4,5-18．(1)y =－x 2－2x +3(2)S =23922t t +(t <－3) (3)P 的坐标为（－4，－5）19．(1)223y x x =+-(2)(3)存在，点F 的坐标为：()1-或()1-或()0,3-或()2,3-- 20．(1)2y x 2x 3=-++(2)点D 的坐标为（0，1）或（0，－1）(3)P （12，154）。

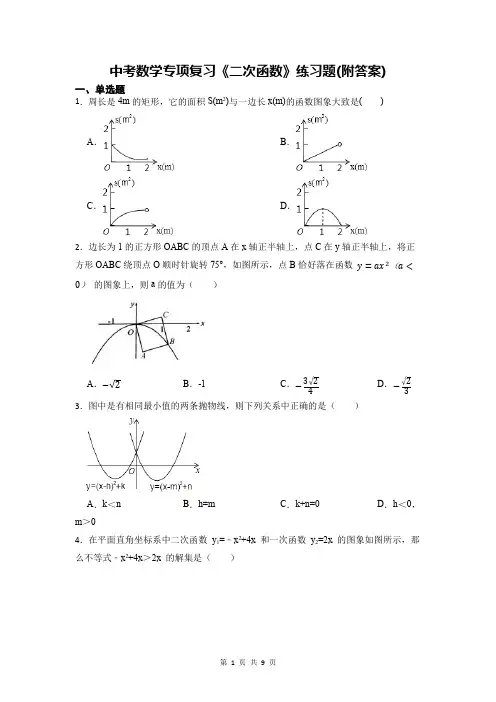
中考数学专项复习《二次函数》练习题(附答案)一、单选题1．周长是4m的矩形，它的面积S(m2)与一边长x(m)的函数图象大致是() A．B．C．D．2．边长为1的正方形OABC的顶点A在x轴正半轴上，点C在y轴正半轴上，将正方形OABC绕顶点O顺时针旋转75°，如图所示，点B恰好落在函数y=ax2（a< 0）的图象上，则a的值为（）A．−√2B．-1C．−3√24D．−√233．图中是有相同最小值的两条抛物线，则下列关系中正确的是（）A．k＜n B．h=m C．k+n=0D．h＜0，m＞04．在平面直角坐标系中二次函数y1=﹣x2+4x 和一次函数y2=2x 的图象如图所示，那么不等式﹣x2+4x＞2x 的解集是（）A．x＜0B．0＜x＜4C．0＜x＜2D．2＜x＜45．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（）A．开口向下B．顶点坐标是（1，2）C．对称轴是x=﹣1D．有最大值是26．已知抛物线y=x2+2x上三点A（﹣5，y1），B（2.5，y2），C（12，y3），则y1，y2，y3满足的关系式为（）A．y1＜y2＜y3B．y3＜y2＜y1C．y2＜y1＜y3D．y3＜y1＜y2A．16B．15C．14D．13 8．一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是（）A．B．C．D．9．已知二次函数y=ax2+bx+c+2的图象如图所示，顶点为（﹣1，0），下列结论：①abc＜0；②b2﹣4ac=0；③a＞0；④4a﹣2b+c＞0．其中正确结论的个数是（）A．1B．2C．3D．4 10．将抛物线y=x2向右平移1个单位长度，再向下平移3个单位长度，所得到的抛物线为（）A．y=(x+1)2+3B．y=(x+1)2−3C．y=(x−1)2+3D．y=(x−1)2−311．已知二次函数y＝ax2+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b2﹣4ac＞0；③3a+c＞0；④（a+c）2＜b2；⑤2a﹣b＜c．其中正确的结论有（）A．1个B．2个C．3个D．4个12．已知抛物线y=x2﹣2bx+4的顶点在x轴上，则b的值一定是（）A．1B．2C．﹣2D．2或﹣2二、填空题13．如图，甲，乙两个转盘分别被三等分、四等分，各转动一次，停止转动后，将指针指向的数字分别记为a，b，使抛物线y=ax2−2x+b与x轴有公共点的概率为．14．将抛物线y=﹣x2+1向右平移2个单位长度，再向上平移3个单位长度所得的抛物线解析式为．15．若抛物线y=2(x−3)2−8与x轴的两个交点分别为点A和点B，则线段AB的长为．16．已知抛物线y=x2﹣x﹣1与x轴的一个交点的横坐标为m，则代数式m2﹣m+2016的值为．17．将抛物线y=x2向右平移2个单位，再向上平移3个单位，所得抛物线的表达式为．18．一个二次函数的图象顶点坐标为（2，1），形状与抛物线y=﹣2x2相同，试写出这个函数解析式三、综合题19．如图，某小区有一块靠墙（墙的长度不限）的矩形空地ABCD，为美化环境，用总长为100m的篱笆围成四块矩形花圃（靠墙一侧不用篱笆，篱笆的厚度不计）.（1）若四块矩形花圃的面积相等，求证：AE＝3BE；（2）在（1）的条件下，设BC的长度为xm，矩形区域ABCD的面积为ym2，求y 与x之间的函数关系式，并写出自变量x的取值范围.20．已知二次函数的图象以A(−1,4)为顶点，且过点B(2,−5)（1）求该函数的关系式；（2）求该函数图象与坐标轴的交点坐标；21．已知拋物线y=x2+bx+c经过点(−1，8)和(2，−7)．（1）试确定b，c的值．（2）直接写出x满足什么条件时y随x的增大而减小．22．已知抛物线y＝ax2＋bx＋5（a为常数，a≠0）交x轴于点A（－1，0）和点B（5，0），交y轴于点C．（1）求点C的坐标和抛物线的解析式；（2）若点P是抛物线上一点，且PB＝PC，求点P的坐标；（3）点Q是抛物线的对称轴l上一点，当QA＋QC最小时求点Q的坐标．23．在平面直角坐标系xOy中抛物线y＝x2﹣2mx+m2﹣1与y轴交于点C．（1）试用含m的代数式表示抛物线的顶点坐标；（2）将抛物线y＝x2﹣2mx+m2﹣1沿直线y＝﹣1翻折，得到的新抛物线与y轴交于点D，若m＞0，CD＝8，求m的值．（3）已知A（﹣k+4，1），B（1，k﹣2），在（2）的条件下，当线段AB与抛物线y＝x2﹣2mx+m2﹣1只有一个公共点时请求出k的取值范围．24．如图，平面直角坐标系中以点C（2，√3）为圆心，以2为半径的圆与x轴交于A，B两点．（1）求A，B两点的坐标；（2）若二次函数y=x2+bx+c的图象经过点A，B，试确定此二次函数的解析式．参考答案1．【答案】D2．【答案】D3．【答案】D4．【答案】C5．【答案】B6．【答案】C7．【答案】B8．【答案】C9．【答案】B10．【答案】D11．【答案】C12．【答案】D13．【答案】11214．【答案】y=﹣（x﹣2）2+415．【答案】416．【答案】201717．【答案】y=(x−2)2+318．【答案】y=﹣2（x﹣2）2+1或y=2（x﹣2）2+119．【答案】（1）证明：∵矩形MEFN与矩形EBCF面积相等∴ME＝BE，MG=GN.∵四块矩形花圃的面积相等，即S矩形AMND＝2S矩形MEFN∴AM＝2ME∴AE＝3BE；（2）解：∵篱笆总长为100m∴2AB+GH+3BC＝100即2AB+12AB+3BC=100∴AB=40−65BC.设BC的长度为xm，矩形区域ABCD的面积为ym2则y=BC⋅AB=x(40−65x)=−65x2+40x∵AB =40−65BC∴B E ＝10﹣ 310x ＞0解得x ＜ 1003∴y =65x 2+40x （0＜x ＜ 1003 ）. 20．【答案】（1）解：由顶点A （−1，4），可设二次函数关系式为y ＝a （x ＋1）2＋4（a≠0）．∵二次函数的图象过点B （2，−5） ∴点B （2，−5）满足二次函数关系式 ∴−5＝a （2＋1）2＋4 解得a ＝−1．∴二次函数的关系式是y ＝−（x ＋1）2＋4； （2）解：令x ＝0，则y ＝−（0＋1）2＋4＝3 ∴图象与y 轴的交点坐标为（0，3）； 令y ＝0，则0＝−（x ＋1）2＋4 解得x 1＝−3，x 2＝1故图象与x 轴的交点坐标是（−3，0）、（1，0）．答：图象与y 轴的交点坐标为（0，3），与x 轴的交点坐标是（−3，0）、（1，0）．21．【答案】（1）解：∵抛物线y =x 2+bx +c 经过点(−1，8)和(2，−7)∴{1−b +c =84+2b +c =−7解得{b =−6c =1；（2）解：由（1）可知，抛物线y =x 2−6x −1开口向上，对称轴为直线x =−−62×1=3 故在对称轴左侧，即当x <3时y 随x 的增大而减小．22．【答案】（1）解：对于y =ax 2+bx +5，当x =0时y =5∴C(0，5)∵抛物线y =ax 2+bx +5(a 为常数，a ≠0)交x 轴于点A(−1，0)和点B(5，0)∴{a −b +5=025a +5b +5=0解得{a =−1b =4∴抛物线的解析式为y =−x 2+4x +5；（2）解：∵B(5，0) C(0，5)∴OB =OC连接BC ，设BC 的中点为D∴D(52，52)∴直线OD 的解析式为y =x∵PB =PC∴点P 在直线OD 上 设P(m ，m)∵点P 是抛物线上一点∴m =−m 2+4m +5解得m =3±√292∴点P 的坐标为(3+√292，3+√292)或(3−√292，3−√292)；（3）解：由（1）知，抛物线的对称轴为直线x =2 ∵点A 与点B 关于l 对称，点Q 在直线l 上 ∴QA =QB QA +QC =QB +QC∴当B ，C ，Q 三点共线时QB +QC 最小，即QA +QC 最小 设直线BC 的解析式为y =kx +b∴{b =55k +b =5解得{k =−1b =5∴直线BC 的解析式为y =−x +5 把x =2代入y =−x +5得，y =3∴Q(2，3)∴当QA +QC 最小时求点Q 的坐标(2，3)．23．【答案】（1）解：∵y ＝x 2﹣2mx+m 2﹣1＝（x ﹣m ）2﹣1∴抛物线的顶点坐标为（m ，﹣1）（2）解：由对称性可知，点C 到直线y ＝﹣1的距离为4 ∴OC ＝3 ∴m 2﹣1＝3 ∵m ＞0 ∴m ＝2（3）解：∵m ＝2，∴抛物线为y ＝x 2﹣4x+3，当抛物线经过点A （﹣k+4，1）时k ＝2+ √2 或k ＝2﹣ √2 ；当抛物线经过点B （1，k ﹣2）时k ＝2；∵线段AB 与抛物线y ＝x 2﹣2mx+m 2﹣1只有一个公共点，则x 2-4x+3=x+k-3∴即x 2-5x+6-k=0的△=0∴25-4（6-k ）=0k=-0.25∵线段AB 与抛物线y ＝x 2﹣2mx+m 2﹣1只有一个公共点∴2﹣ √2 ＜k ＜2或k≥2+ √2 或k=-0.25．24．【答案】（1）解：过点C 作CM△x 轴于点M ，则MA=MB ，连结AC ，如图∵点C 的坐标为（2， √3 ） ∴OM=2 CM= √3 在Rt△ACM 中CA=2 ∴AM= √AC 2−CM 2 =1∴OA=OM ﹣AM=1 OB=OM+BM=3 ∴A 点坐标为（1，0），B 点坐标为（3，0）；（2）解：将A （1，0），B （3，0）代入y=x 2+bx+c 得 {1+b +c =09+3b +c =0解得 {b =−4c =3．所以二次函数的解析式为y=x 2﹣4x+3．。

2020届中考数学二轮复习专题训练：二次函数与几何1. 如图，抛物线1C :y ＝ax 2＋bx+1的顶点坐标为D （1,0），（1）求抛物线1C 的解析式；（2）如图1，将抛物线1C 向右平移1个单位，向下平移1个单位得到抛物线2C ，直线y x c =+，经过点D 交y 轴于点A ，交抛物线2C 于点B ，抛物线2C 的顶点为P,求△DBP 的面积（3）如图2，连结AP,过点B 作BC ⊥AP 于C,设点Q 为抛物线上点P 至点B 之间的一动点，连结PQ 并延长交BC 于点E ，连结 BQ 并延长交AC 于点F ，试证明：()FC AC EC +为定值．图1yxO P DBA图2QyxO P F E CDB A【解答】（1）∵抛物线顶点为(1,0)P ，经过点（0,1）∴可设抛物线的解析式为：2(1)y a x =-，得： 1a = ∴抛物线的解析式为221y x x =-+（2）根据题意的p （2，-1）∴抛物线的解析式为：2(2)1y x =--，∴A(0，-1),B(4,3)∴△DBP 的面积 =3（3）过点Q 作QM AC ⊥于点M ，过点Q 作QN BC ⊥于点N ，设点Q 的坐标是2(,43)t t t -+，则2(2)QM CN t ==-，4MC QN t ==-.∵//QM CE ∴PQM ∆∽PEC ∆ ∴QM PM EC PC = 即2(2)12t t EC --=，得2(2)EC t =- ∵//QN FC ∴BQN ∆∽BFC ∆ ∴QN BN FC BC = 即243(43)4t t t FC ---+=，得4FC t = 又∵4AC =∴4()[42(2)]8FC AC EC t t+=+-==，即()FC AC EC +为定值8.2. 如图，已知抛物线C 1：()522-+=x a y 的顶点为P ，与x 轴相交于A 、B 两点（点A 在点B 的左边），点B 的横坐标是1．（1）求P 点坐标及a 的值；（3分）（2）如图1，抛物线C 2与抛物线C 1关于x 轴对称，将抛物线C 2向右平移，平移后的抛物线记为C 3，C 3的顶点为M ，当点P 、M 关于点B 成中心对称时，求C 3的解析式；（4分） （3）如图2，点Q 是x 轴正半轴上一点，将抛物线C 1绕点Q 旋转180°后得到抛物线C 4．抛物线C 4的顶点为N ，与x 轴相交于E 、F 两点（点E 在点F 的左边），当以点P 、N 、F 为顶点的三角形是直角三角形时，求点Q 的坐标．（5分）（1）由抛物线C 1：()522-+=x a y 得顶点P 的为（-2，-5）∵点B （1，0）在抛物线C 1上∴()52102-+=a ，∴a ＝59 （2）连接PM ，作PH ⊥x 轴于H ，作MG ⊥x 轴于G∵点P 、M 关于点B 成中心对称，∴PM 过点B ，且PB ＝MB ∴△PBH ≌△MBG ，∴MG ＝PH ＝5，BG ＝BH ＝3∴顶点M 的坐标为（4，5），抛物线C 2由C 1关于x 轴对称得到，抛物线C 3由C 2平移得到∴抛物线C 3的表达式为()54952+--=x y （3）∵抛物线C 4由C 1绕点x 轴上的点Q 旋转180°得到∴顶点N 、P 关于点Q 成中心对称由（2）得点N 的纵坐标为5设点N 坐标为（m ，5） 作PH ⊥x 轴于H ，作NG ⊥x 轴于G ，作PK ⊥NG 于K ∵旋转中心Q 在x 轴上 ∴EF ＝AB ＝2BH ＝6 ∴FG ＝3，点F 坐标为（m +3，0）H 坐标为（2，0），K 坐标为（m ，-5）， 根据勾股定理得 PN 2＝NK 2+PK 2＝m 2+4m +104PF 2＝PH 2+HF 2＝m 2+10m +50 NF 2＝52+32＝34①当∠PNF ＝90º时，PN 2+ NF 2＝PF 2，解得m ＝443，∴Q 点坐标为（193，0）②当∠PFN ＝90º时，PF 2+ NF 2＝PN 2，解得m ＝103，∴Q 点坐标为（23，0） ③∵PN ＞NK ＝10＞NF ，∴∠NPF ≠90º综上所得，当Q 点坐标为（193，0）或（23，0）时，以点P 、N 、F 为顶点的三角形是直角三角形．3. 已知: 如图1, 二次函数y ＝a (x －1)2－4的图象交x 轴负半轴于点A , 交x 轴正半轴于点B , 交y 轴负半轴于点C , 且OB ＝3OA . (1) 求二次函数的解析式;(2) 如图2, M 是抛物线的顶点, P 是抛物线在B 点右侧上一点, Q 是对称轴上一点, 并且AQ ⊥PQ , 是否存在这样的点P , 使得∠P AQ ＝∠AMQ ? 若存在, 请求出P 点坐标; 若不存在, 请说明理由.（3）如图3, 设(1)中抛物线的顶点为M ,R 为x 轴正半轴上一点，将（1）中抛物线绕R 旋转1800得到抛物线C 1: y ＝-a (x －h)2+k 交x 轴于D,E 两点，.若tan ∠BME=1,求R 点的坐标。

《二次函数综合》压轴题专题训练1．定义：关于x轴对称且对称轴相同的两条抛物线叫作“同轴对称抛物线”．例如：y＝（x﹣1）2﹣2的“同轴对称抛物线”为y＝﹣（x﹣1）2+2．（1）满足什么条件的抛物线与其“同轴对称抛物线”的顶点重合：．（2）求抛物线y＝﹣x2+x+1的“同轴对称抛物线”．（3）如图，在平面直角坐标系中，点B是抛物线L：y＝ax2﹣4ax+1上一点，点B的横坐标为1，过点B作x轴的垂线，交抛物线L的“同轴对称抛物线”于点C，分别作点B、C关于抛物线对称轴对称的点B′、C′，连接BC、CC′、B′C′、BB′，设四边形BB′C′C的面积为S（S＞0）．①当四边形BB′C′C为正方形时，求a的值．②当抛物线L与其“同轴对称抛物线”围成的封闭区域内（不包括边界）共有11个横、纵坐标均为整数的点时，直接写出a的取值范围．2．已知抛物线C：y＝ax2+bx+c向左平移1个单位长度，再向上平移4个单位长度得到抛1物线C：y＝x2．2（1）直接写出抛物线C的解析式；1与x轴交于A，B两点，点A在点B的左侧，点P（，t）（2）如图1，已知抛物线C1在抛物线C上，QB⊥PB交抛物线于点Q．求点Q的坐标；1上，EM∥x轴，点E在点M的左侧，过点M的直线MD与抛（3）已知点E，M在抛物线C2物线C只有一个公共点（MD与y轴不平行），直线DE与抛物线交于另一点N．若线段2NE＝DE，设点M，N的横坐标分别为m，n，直接写出m和n的数量关系（用含m的式子表示n）为．3．如图1，抛物线y＝x2+bx+c过点A（4，﹣1），B（0，﹣），点C为直线AB下方抛物线上一动点，M为抛物线顶点，抛物线对称轴与直线AB交于点N．（1）求抛物线的表达式与顶点M的坐标；（2）在直线AB上是否存在点D，使得以C，D，M，N为顶点的四边形是平行四边形，若存在，请求出D点坐标；（3）在y轴上是否存在点Q，使∠AQM＝45°？若存在，求点Q的坐标；若不存在，请说明理由．4．如图，已知抛物线y＝ax2+bx+c与x轴的交点为A（﹣1，0），B（2，0）且与y轴交于点C，OA＝OC．（1）求该抛物线的表达式；（2）点C关于x轴的对称点为C1，M是线段BC1上的一个动点（不与B、C1重合），ME⊥x轴，MF⊥y轴，垂足分别为E、F，当点M在什么位置时，矩形MFOE的面积最大？说明理由；（3）已知点P时直线y＝x+1上的动点，点Q为抛物线上的动点，当以C、C1、P、Q 为顶点的四边形为平行四边形时，求出相应的点P和点Q的坐标．5．如图，抛物线y＝﹣x2+bx+c与x轴相交于A，B两点（点A位于点B的左侧），与y轴相交于点C，M是抛物线的顶点，直线x＝1是抛物线的对称轴，且点C的坐标为（0，3）．（1）求抛物线的解析式；（2）已知P为线段MB上一个动点，过点P作PD⊥x轴于点D．若PD＝m，△PCD的面积为S．①求S与m之间的函数关系式，并写出自变量m的取值范围；②当S取得最值时，求点P的坐标．（3）在（2）的条件下，在线段MB上是否存在点P，使△PCD为等腰三角形？如果存在，请求出点P的坐标；如果不存在，请说明理由．6．如图1，抛物线y＝ax2+bx+c（a≠0）的顶点为C（1，4），交x轴于A、B两点，交y 轴于点D，其中点B的坐标为（3，0）．（1）求抛物线的解析式；＝3，请求出点P的坐标．（2）如图2，点P为直线BD上方抛物线上一点，若S△PBD（3）如图3，M为线段AB上的一点，过点M作MN∥BD，交线段AD于点N，连接MD，若△DNM∽△BMD，请求出点M的坐标．7．已知抛物线交x轴于A，B两点（A在B右边），A（3，0），B（1，0）交y轴于C点，C（0，3），连接AC；（1）求抛物线的解析式；（2）P为抛物线上的一点，作PE⊥CA于E点，且CE＝3PE，求P点坐标；（3）将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点，过H作直线MH，NH，当MH⊥NH时，求MN恒过的定点坐标．：y＝（x﹣1）2+k（k＞0）经过y轴上的点A，顶点为B．抛物线8．如图，已知抛物线l1l：y＝（x﹣h）2+2﹣h（h≥2）的顶点为D，直线y＝﹣x+b经过A，B，D三点，两抛物2线交于点C．（1）求b的值和点B的坐标；（2）设点C的横坐标为m，探究m与h之间的数量关系；（3）当△ABC是直角三角形时，求h的值．9．综合与探究．如图1，抛物线y＝x2﹣x﹣2与x轴交于A，B两点，与y轴交于点C，经过点B的直线交y轴于点E（0，2）．（1）求A，B，C三点的坐标及直线BE的解析式．（2）如图2，过点A作BE的平行线交抛物线于点D，点P是抛物线上位于线段AD下方的一个动点，连接PA，PD，求OAPD面积的最大值．（3）若（2）中的点P为抛物线上一动点，在x轴上是否存在点Q，使得以A，D，P，Q 为顶点的四边形是平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．10．如图，抛物线y＝ax2+bx+c与x轴交于A（1，0）、B（3，0）两点，与y轴交于点C（0，3），抛物线的对称轴与直线BC交于点D．（1）求抛物线的表达式；（2）在抛物线的对称轴上找一点M，使|BM﹣CM|的值最大，求出点M的坐标；（3）点E为直线BC上一动点，过点E作y轴的平行线EF，与抛物线交于点F问是否存在点E，使得以D、E、F为顶点的三角形与△BCO相似？若存在，直接写出点E的坐标．11．如图1，抛物线y＝ax2+2ax+c（a≠0）与x轴交于点A，B（1，0）两点，与y轴交于点C，且OA＝OC．（1）求抛物线的解析式；（2）点D是抛物线顶点，求△ACD的面积；（3）如图2，射线AE交抛物线于点E，交y轴的负半轴于点F（点F在线段AE上），点P是直线AE下方抛物线上的一点，S＝，求△APE面积的最大值和此动点P的坐标．△ABE12．图①，抛物线y＝﹣2x2+bx+c过A（﹣1，0）、B（3，0）两点，交y轴于点C，连接BC．（1）求该抛物线的表达式和对称轴；（2）点D是抛物线对称轴上一动点，当△BCD是以BC为直角边的直角三角形时，求所有符合条件的点D的坐标；（3）如图2，将抛物线在BC上方的图象沿BC折叠后与y轴交与点E，求点E的坐标．13．已知，抛物线y＝ax2，其中a＞0．（1）如图1，若点A、B是此抛物线上两点，且分属于y轴两侧，连接AB与y轴相交于点C，且∠AOB＝90°．求证：CO＝；（2）如图2，若点A是此抛物线上一点，过点A的直线恰好与此抛物线仅有一个交点，且与y轴交于点B，与x轴相交于点C．求证：AC＝BC．14．如图，抛物线y＝ax2﹣x+c与x轴交于A，B两点，与y轴交于C点，连结AC，已知B（1﹣，0），且抛物线经过点D（2，﹣2）．（1）求抛物线的解析式；（2）若点E是抛物线上位于x轴下方的一点，且S△ACE ＝S△ABC，求E的坐标；（3）若点P是y轴上一点，以P、A、C三点为顶点的三角形是等腰三角形，求P点的坐标．15．如图，在平面直角坐标系中，直线y＝﹣x+4分别与x轴、y轴相交于点B、C，经过点B、C的抛物线y＝﹣+bx+c与x轴的另一个交点为A．（1）求出抛物线表达式，并求出点A坐标．（2）已知点D在抛物线上，且横坐标为3，求出△BCD的面积；（3）点P是直线BC上方的抛物线上一动点，过点P作PQ垂直于x轴，垂足为Q．是否存在点P，使得以点A、P、Q为顶点的三角形与△BOC相似？若存在，请求出点P的坐标；若不存在，请说明理由．参考答案1．解：（1）∵“同轴对称抛物线”的顶点重合，∴顶点关于x轴对称且重合，∴顶点在x轴上，故答案为：顶点在x轴上；（2）∵y＝﹣x2+x+1＝﹣（x﹣1）2+，∴“同轴对称抛物线”的顶点坐标为（1，﹣），∴y＝（x﹣1）2﹣；（3）①由题可知，B（1，1﹣3a），∴C（1，3a﹣1），∵抛物线y＝ax2﹣4ax+1的对称轴为x＝2，∴B'（3，1﹣3a），C'（3，3a﹣1），∴BB'＝CC'＝2，∴BC＝2﹣6a或BC＝6a﹣2，∴2﹣6a＝2或6a﹣2＝2，∴a＝0（舍去）或a＝；②函数的对称轴为x＝2，函数L的顶点坐标为（2，1﹣4a），∵L与“同轴对称抛物线”是关于x轴对称的，所以整数点也是对称的出现，∵抛物线L与其“同轴对称抛物线”围成的封闭区域内，在x轴上的整数点可以是3个或5个，∴L与x轴围城的区域的整数点为4个或3个；当a＞0时，当x＝1时，﹣2≤1﹣3a＜﹣1，∴＜a≤1，当x＝2时，1﹣4a＜﹣2，∴a＞，∴＜a≤1；当a＜0时，当x＝2时，1﹣4a≤2，∴a≥﹣，当x＝﹣1时，5a+1＜0，∴a＜﹣，∴﹣≤a＜﹣；综上所述：＜a≤1或﹣≤a＜﹣．2．解：（1）由已知可知，抛物线C：y＝x2向右平移1个单位长度，再向下平移4个单位2：y＝ax2+bx+c，长度得到抛物线C1：y＝（x﹣1）2﹣4，∴抛物线C1故答案为y＝（x﹣1）2﹣4；（2）∵y＝（x﹣1）2﹣4，令y＝0，（x﹣1）2﹣4＝0，解得x＝3或x＝﹣1，∴A（﹣1，0），B（3，0），上，∵点P（，t）在抛物线C1∴t＝（﹣1）2﹣4，解得t＝﹣，∴P（，﹣），设Q（t，t2﹣2t﹣3），过点P作PM⊥x轴交于点M，过点Q作QN⊥x轴交于点N，∵BQ⊥BP，∴∠QBN+∠MBP＝∠QBN+∠MQN＝90°，∴∠BQN＝∠PBM，∴△BNQ∽△QMP，∴＝，∴＝，∴t＝﹣或t＝3，∵Q点在第二象限，∴t＝﹣，∴Q（﹣，）；（3）∵点M与N在y＝x2上，∴M（m，m2），N（n，n2）∵EM∥x轴，∴E（﹣m，m2），设MD的解析式为y＝kx+b，∴m2＝km+b，∴b＝m2﹣km，∴y＝kx+m2﹣km，∵直线MD与抛物线y＝x2只有一个交点，∴kx+m2﹣km＝x2，∴△＝k2﹣4（m2+km）＝0，∴k＝2m，∴直线MD的解析式为y＝2mx﹣m2，∵NE＝DE，∴D（﹣2m﹣n，2m2﹣n2），∴2m2﹣n2＝2m（﹣2m﹣n）﹣m2，整理得，n2﹣2mn﹣7m2＝0，∴n＝（1±2）m，故答案为n＝（1±2）m．3．解：（1）将点A（4，﹣1），B（0，﹣）代入抛物线y＝x2+bx+c，得，解得，∴y＝x2﹣x﹣，∴M点的坐标为（1，﹣4）；（2）设直线AB的表达式为y＝mx+n，∴，解得，∴y＝x﹣；当x＝1时，y＝﹣3，∴N（1，﹣3），∴MN＝1；①若MN为平行四边形的一边时，则有CD∥MN，且CD＝MN，设C（t，t2﹣t﹣），则D（t，t﹣），∴CD＝t﹣﹣（t2﹣t﹣）＝1，∴t＝3或t＝1（舍去），∴D（3，﹣）；②若MN为平行四边形的对角线，设D（t，t﹣），则C（2﹣t，﹣t﹣），将点C代入抛物线解析式得，（2﹣t）2﹣（2﹣t）﹣＝﹣t﹣，∴t＝﹣1或t＝1（舍去），∴D（﹣1，﹣）；综上所述：符合条件的D点坐标为（3，﹣）或（﹣1，﹣）；（3）在对称轴上取点P（1，﹣1），∴PA＝PM＝3，∠APM＝90°，以P为圆心，PA为半径作圆交y轴于点Q，∴∠AQM＝∠APM＝45°，作PE⊥y轴交于点E，∴PE＝1，∵PQ＝3，∴EQ＝＝2，∴Q点坐标为（0，﹣1+2）或（0，﹣1﹣2）．4．解：（1）∵点A （﹣1，0） ∴OA ＝1，∵OA ＝OC ＝1，且点C 在y 轴负半轴， ∴点C （0，﹣1）∵抛物线y ＝ax 2+bx +c 与x 轴的交点为A （﹣1，0），B （2，0）且与y 轴交于点C ， ∴解得：∴抛物线的表达式为：y ＝x 2﹣x ﹣1； （2）∵点C 关于x 轴的对称点为C 1， ∴C 1（0，1），∵点B （2，0），点C 1（0，1）， ∴直线BC 1的解析式为：y ＝﹣x +1， ∴设点M 坐标为（m ，﹣m +1） ∴MF ＝m ，ME ＝﹣m +1，∴矩形MFOE 的面积＝MF ×ME ＝m ×（﹣m +1）＝﹣m 2+m ＝﹣（m ﹣1）2+， ∴当m ＝1时，矩形MFOE 的最大面积为，此时点M 的坐标为（1，），即点M 为线段C 1B 中点时，S 矩形MFOE 最大；（3）由题意，C （0，﹣1），C 1（0，1），以C 、C 1、P 、Q 为顶点的四边形为平行四边形，分以下两种情况：①C 1C 为边，则C 1C ∥PQ ，C 1C ＝PQ ， 设P （m ，m +1），Q （m ，m 2﹣m ﹣1）， ∴|（m 2﹣m ﹣1）﹣（m +1）|＝2， 解得：m 1＝4，m 2＝﹣2，m 3＝2，m 4＝0（舍），P 1（4，3），Q 1（4，5）；P 2（﹣2，0），Q 2（﹣2，2）；P 3（2，2），Q 3（2，0）②C 1C 为对角线，∵C 1C 与PQ 互相平分，C 1C 的中点为（0，0）， ∴PQ 的中点为（0，0），设P （m ，m 2﹣m +1），则Q （﹣m ，m 2+m ﹣1） ∴（m +1）+（m 2+m ﹣1）＝0， 解得：m 1＝0（舍去），m 2＝﹣2， ∴P 4（﹣2，0），Q 4（2，0）；综上所述，点P 和点Q 的坐标为：P 1（4，3），Q 1（4，5）或P 2（﹣2，0），Q 2（﹣2，2）或P 3（2，2），Q 3（2，0）或P 4（﹣2，0），Q 4（2，0）．5．解：（1）∵直线x ＝1是抛物线的对称轴，且点C 的坐标为（0，3）， ∴c ＝3，﹣＝1，∴b ＝2，∴抛物线的解析式为：y ＝﹣x 2+2x +3； （2）①∵y ＝﹣x 2+2x +3＝﹣（x ﹣1）2+4， ∴点M （1，4），∵抛物线的解析式为：y ＝﹣x 2+2x +3与x 轴相交于A ，B 两点（点A 位于点B 的左侧）， ∴0＝﹣x 2+2x +3 ∴x 1＝3，x 2＝﹣1，∴点A （﹣1，0），点B （3，0）， ∵点M （1，4），点B （3，0） ∴直线BM 解析式为y ＝﹣2x +6，∵点P 在直线BM 上，且PD ⊥x 轴于点D ，PD ＝m ， ∴点P （3﹣，m ），∴S △PCD ＝×PD ×OD ＝m ×（3﹣）＝﹣m 2+m ， ∵点P 在线段BM 上，且点M （1，4），点B （3，0）， ∴0＜m ≤4∴S与m之间的函数关系式为S＝﹣m2+m（0＜m≤4）②∵S＝﹣m2+m＝﹣（m﹣3）2+，∴当m＝3时，S有最大值为，∴点P（，3）∵0＜m≤4时，S没有最小值，综上所述：当m＝3时，S有最大值为，此时点P（，3）；（3）存在，若PC＝PD＝m时，∵PD＝m，点P（3﹣，m），点C（0，3），∴（3﹣﹣0）2+（m﹣3）2＝m2，∴m1＝18+6（舍去），m2＝18﹣6，∴点P（﹣6+3，18﹣6）；若DC＝PD＝m时，∴（3﹣﹣0）2+（﹣3）2＝m2，∴m3＝﹣2﹣2（舍去），m4＝﹣2+2，∴点P（4﹣，﹣2+2）；若DC＝PC时，∴（3﹣﹣0）2+（m﹣3）2＝（3﹣﹣0）2+（﹣3）2，∴m5＝0（舍去），m6＝6（舍去）综上所述：当点P的坐标为：（﹣6+3，18﹣6）或（4﹣，﹣2+2）时，使△PCD为等腰三角形．6．解：（1）设抛物线的解析式为y＝a（x﹣1）2+4，将点B（3，0）代入得，（3﹣1）2×a+4＝0．解得：a＝﹣1．∴抛物线的解析式为：y＝﹣（x﹣1）2+4＝﹣x2+2x+3．（2）过点P作PQ∥y轴交DB于点Q，∵抛物线的解析式为y＝﹣x2+2x+3∴D（0，3）．设直线BD的解析式为y＝kx+b，∴，解得：，∴直线BD的解析式为y＝﹣x+3．设P（m，﹣m2+2m+3），则Q（m，﹣m+3），∴PQ＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m．∵S△PBD ＝S△PQD+S△PQB，∴S△PBD＝（3﹣m）＝PQ＝﹣m，∵S△PBD＝3，∴﹣m＝3．解得：m1＝1，m2＝2．∴点P的坐标为（1，4）或（2，3）．（3）∵B（3，0），D（0，3），∴BD＝＝3，设M（a，0），∵MN∥BD，∴△AMN∽△AMD，∴，即．∴MN＝（1+a），DM＝＝，∵△DNM∽△BMD，∴，∴DM2＝BD•MN．∴9+a2＝3（1+a）．解得：a＝或a＝3（舍去）．∴点M的坐标为（，0）．7．解：（1）∵抛物线过A（3，0），B（1，0），∴可设抛物线的解析式为y＝a（x﹣3）（x﹣1）（a≠0），把c（0，3）代入，得3a＝3，∴a＝1，∴抛物线的解析式是y＝（x﹣3）（x﹣1）＝x2﹣4x+3，即y＝x2﹣4x+3；（2）过点P作PD⊥x轴于点D，过E作EF⊥y轴于F，延长FE与PD交于点G，如图1，∵A（3，0），C（0，3），∴OA＝OC＝3，∴∠OAC＝45°，∵FG∥OA，∴∠CEF＝45°，∴CF＝EF＝CE，∵PE⊥CA，∴∠PEG＝45°，∴PG＝EG＝PE，∵CE＝3PE，∴EF＝3FG，设EF＝3m，则PG＝EG＝m，FG＝4m，∴DG＝OF＝OC﹣CF＝3﹣3m，PD＝PG+DG＝3﹣2m，∴P（4m，3﹣2m），把P（4m，3﹣2m）代入y＝x2﹣4x+3中得，3﹣2m＝16m2﹣16m+3，∴m＝，或m＝0（舍去），∴P（，）；（3）∵y＝x2﹣4x+3＝（x﹣2）2﹣1，∴抛物线y＝x2﹣4x+3的顶点为（2，﹣1），∵将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点，∴H（2，0），由题意知，点H是新抛物线的顶点，∴新抛物线的解析式为y＝（x﹣2）2，设M（m，（m﹣2）2），N（n，（n﹣2）2），过M作MK⊥x轴于点K，过点N作NL⊥x轴于点L，则MK＝（m﹣2）2，KH＝2﹣m，HL＝n﹣2，NL＝（n﹣2）2，∵MH⊥NH，∴∠MHK+∠HMK＝∠MHK+∠NHL＝90°，∴∠HMK＝∠NHL，∵∠MKH＝∠HLN＝90°，∴△KHM∽△LNH，∴，，∴，∴，设直线MN的解析式为：y＝kx+b（k≠0），则，∴，∴直线MN的解析式为：，当x＝2时，y＝﹣（m2﹣4m+3）＝m2﹣4m+4﹣m2+4m﹣3＝1，∴MN恒过的定点（2，1）．8．解：（1）∵y＝（x﹣1）2+k（k＞0）经过y轴上的点A，顶点为B，∴A（0，1+k），B（1，k），∵y＝（x﹣h）2+2﹣h（h≥2）的顶点为D，∴D（h，2﹣h），∵直线y＝﹣x+b经过A，D，∴，∴，∴b的值为2，点B的坐标为（1，1）；：y＝（x﹣1）2+1，（2）由（1）知，抛物线l1∵点C的横坐标为m，两抛物线交于点C．∴（m﹣1）2+1＝（m﹣h）2﹣h+2，整理得2mh﹣2m＝h2﹣h∵h≥2∴m＝＝；（3）当AC⊥AB时，则直线AC解析式为：y＝x+2，∴∴（舍去），，∴点C坐标为（3，5），∴3＝∴h＝6；当BC⊥AB时，则直线BC解析式为：y＝x，∴∴（舍去），∴点C坐标为（2，2），∴2＝∴h＝4；9．解：（1）令y＝0，则x2﹣x﹣2＝0，解得x＝4或x＝﹣1，∴A（﹣1，0），B（4，0），令x＝0，则y＝﹣2，∴C（0，﹣2），设直线BE的解析式为y＝kx+b，将B（4，0）、E（0，2）代入得，，解得：，∴y＝﹣x+2；（2）由题意可设AD的解析式为y＝﹣x+m，将A（﹣1，0）代入，得到m＝﹣，∴y＝﹣x﹣，联立，解得：，，∴D（3，﹣2），过点P作PF⊥x轴于点F，交AD于点N，过点D作DG⊥x轴于点G．∴S△APD ＝S△APN+S△DPN＝PN•AF+PN•FG＝PN（AF+FG）＝PN•AG＝×4PN＝2PN，设P（a，﹣a2﹣a﹣2），则N（a，﹣a﹣），∴PN＝﹣a2+a+，∴S△APD＝﹣a2+2a+3＝﹣（a﹣1）2+4，∵﹣1＜0，﹣1＜a＜3，∴当a＝1时，△APD的面积最大，最大值为4；（3）存在；①当PD与AQ为平行四边形的对边时，∵AQ∥PD，AQ在x轴上，∴P（0，﹣2），∴PD＝3，∴AQ＝3，∵A（﹣1，0），∴Q（2，0）或Q（﹣4，0）；②当PD与AQ为平行四边形的对角线时，PD与AQ的中点在x轴上，∴P点的纵坐标为2，∴P（，2）或P（，2），∴PD的中点为（，0）或（，0），∵Q点与A点关于PD的中点对称，∴Q（，0）或Q（，0）；综上所述：点Q的坐标为（2，0）或（﹣4，0）或（，0）或（，0）．10．解：（1）∵抛物线y＝ax2+bx+c经过点A（1，0）、B（3，0）、C（0，3），∴，解得，∴抛物线的表达式为y＝x2﹣4x+3；（2）∵抛物线对称轴是线段AB的垂直平分线，∴AM＝BM，由三角形的三边关系，|BM﹣CM|＝|AM﹣CM|＜AC，∴点A、C、M三点共线时，|BM﹣CM|最大，设直线AC的解析式为y＝mx+n，则，解得，又∵抛物线对称轴为直线x ＝﹣＝2，∴x ＝2时，y ＝﹣3×2+3＝﹣3， 故，点M 的坐标为（2，﹣3）； （3））∵OB ＝OC ＝3，OB ⊥OC ， ∴△BOC 是等腰直角三角形，∵EF ∥y 轴，直线BC 的解析式为y ＝﹣x +3， ∴△DEF 只要是直角三角形即可与△BOC 相似， ∵D （2，1），A （1，0），B （3，0）， ∴点D 垂直平分AB 且到点AB 的距离等于AB ， ∴△ABD 是等腰直角三角形， ∴∠ADB ＝90°， 如图，①点F 是直角顶点时，点F 的纵坐标与点D 的纵坐标相同，是1， ∴x 2﹣4x +3＝1， 整理得x 2﹣4x +2＝0， 解得x ＝2±，当x ＝2﹣时，y ＝﹣（2﹣）+3＝1+， 当x ＝2+时，y ＝﹣（2+）+3＝1﹣， ∴点E 1（2﹣，1+）E 2（2+，1﹣），②点D 是直角顶点时，联立，解得，，当x ＝1时，y ＝﹣1+3＝2， 当x ＝4时，y ＝﹣4+3＝﹣1， ∴点E 3（1，2），E 4（4，﹣1）， 综上所述，存在点E 1（2﹣，1+）或E 2（2+，1﹣）或E 3（1，2）或E 4（4，﹣1），使以D 、E 、F 为顶点的三角形与△BCO 相似．11．解：（1）∵抛物线y ＝ax 2+2ax +c （a ≠0）与x 轴交于点A ，B （1，0）两点，与y 轴交于点C ，且OA ＝OC ，∴a +2a +c ＝0，点C 的坐标为（0，c ）， ∴点A 的坐标为（c ，0）， ∴ac 2+2ac +c ＝0， ∴，解得，或，∵函数图象开口向上， ∴a ＞0， ∴a ＝1，c ＝﹣3，∴抛物线的解析式为y ＝x 2+2x ﹣3；（2）∵y ＝x 2+2x ﹣3＝（x +1）2﹣4，抛物线与与y 轴交于点C ，顶点为D ，OA ＝OC ，抛物线y ＝ax 2+2ax +c （a ≠0）与x 轴交于点A ，B （1，0）两点，∴点D 的坐标为（﹣1，﹣4），点C 的坐标为（0，﹣3），点A 的坐标为（﹣3，0）， 连接OD ，如右图1所示， 由图可知：S △ACD ＝S △OAD +S △OCD ﹣S △OAC＝＝3；（3）∵A（﹣3，0），点B（1，0），∴AB＝4，设点E的纵坐标为t，t＜0，∵S△ABE＝，∴＝，得t＝，把y＝﹣代入y＝x2+2x﹣3，得﹣＝x2+2x﹣3，解得，x1＝，x2＝，∵点E在y轴的右侧，∴点E（，﹣），设直线AE的解析式为y＝mx+n（m≠0），∴，得，∴直线AE的解析式为y＝﹣x﹣1，过点P作y轴的平行线交AC于点G，如图2所示，设点P的横坐标为x，则P（x，x2+2x﹣3），点G（x，﹣x﹣1），∴PG＝（﹣x﹣1）﹣（x2+2x﹣3）＝﹣x2﹣x+2，又∵A（﹣3，0），E（，﹣），∴S△APE ＝S△APG+S△PEG＝（﹣x2﹣x+2）（x+3）+（﹣x2﹣x+2）（﹣x）＝（﹣x2﹣x+2）（3+）＝（x+）2+，∴当x＝﹣时，S取得最大值，最大值是，△APE把x＝﹣代入y＝x2+2x﹣3，得y＝（﹣）2+2×（﹣）﹣3＝﹣，∴此时点P的坐标为（﹣，﹣）．12．解：（1）∵抛物线y＝﹣2x2+bx+c过A（﹣1，0）、B（3，0）两点，∴，得，∴y＝﹣2x2+4x+6＝﹣2（x﹣1）2+8，∴抛物线的对称轴是直线x＝1，即该抛物线的解析式为y＝﹣2x2+4x+6，对称轴是直线x＝1；（2）分两种情况：设点D的坐标为（1，y）第一种情况是：∠BCD＝90°时，则CD2+BC2＝BD2，∵点B的坐标为（3，0），抛物线y＝﹣2x2+4x+6交y轴于点C，∴点C的坐标为（0，6），∴[12+（y﹣6）2]+（32+62）＝（3﹣1）2+y2，解得，y＝6.5，∴点D的坐标为（1，6.5）；第二种情况：当∠DBC＝90°时，BD2+BC2＝CD2，即[（3﹣1）2+y2]+（32+62）＝12+（6﹣y）2，解得，y＝﹣1，∴点D的坐标为（1，﹣1），综上所述，符合条件的点D的坐标为（1，6.5），（1，﹣1）；（3）因为点C的坐标为（0，6），点B的坐标为（3，0），设直线BC的解析式为y＝kx+6，则3k+6＝0，得k＝﹣2，即直线BC的解析式为y＝﹣2x+6，如右图所示，作点E关于直线BC的对称点E′交BC于点F，过点F作FN⊥y轴于点N，设E（0，m），E′（x，y），则EE′⊥BC，∴∠CFE＝∠COB＝90°，∴BC＝＝3，∵∠ECF＝∠BCO，∴△ECF∽△BCO，∴，即，解得，CF＝，又∵∠CNF＝∠COB，∠NCF＝∠OCB，∴△NCF∽△OCB，∴，即，解得，FN＝，∴点F的横坐标为，把x＝代入直线BC的解析式，得y＝，∴点F的坐标为（，），∵EE′关于直线BC对称，∴点F为EE′的中点，∴，解得，∴E′（，），∵点E′在抛物线y＝﹣2x2+4x+6上，∴＝﹣2×[]2+4×+6，解得，m1＝6，m2＝，∴点E的坐标为（0，6）或（0，）．13．证明：（1）设A（b，ab2），B（c，ac2），∵∠AOB＝90°，∴AB2＝AO2+BO2，∴（b﹣c）2+（ab2﹣ac2）2＝b2+a2b4+c2+a2c4，﹣2bc﹣2a2b2c2＝0，1+a2bc＝0，∴bc＝﹣，设直线AB的解析式为：y＝mx+n，则，解得，∴直线AB的解析式为：y＝a（b+c）x﹣abc，当x＝0时，y＝OC＝﹣abc＝﹣a•（﹣）＝；（2）如图2，过A作AD⊥y轴于D，设直线AB的解析式为：y＝kx+b，当y＝0时，kx+b＝0，∴x＝﹣，∴OC＝﹣，∵过点A的直线AB恰好与此抛物线仅有一个交点，∴ax2＝kx+b，∴ax2﹣kx﹣b＝0，△＝k2+4ab＝0，∴b ＝﹣，OC ＝﹣＝，∴x ＝，∵a ＞0，k ＞0，∴AD ＝，∵AD ∥OC ，∴＝＝，∴AB ＝2BC ，∴AC ＝BC ．14．解：（1）把B （﹣1，0），D （2，﹣2）代入y ＝ax 2﹣x +c 得， 解得：．故抛物线的解析式为y ＝x 2﹣x ﹣2；（2）当y ＝0时，x 2﹣x ﹣2＝0，解得x 1＝﹣1，x 2＝3，∴A （3，0），∴AB ＝4，当x ＝0时，y ＝﹣2，∴C （0，﹣2），∴OC ＝2，∴S △ABC ＝×4×2＝4，设AC 的解析式为y ＝kx +b ，把A （3，0），C （0，﹣2）代入y ＝kx +b 得， 解得．∴y ＝x ﹣2，如图1，过点E 作x 轴的垂线交直线AC 于点F ，设点F （a ，a ﹣2），点E （a ，a 2﹣a ﹣2），其中﹣1＜a ＜3，∴S △ACE ＝EF |x A ﹣x C |＝|a 2﹣a |＝，∵S △ACE ＝S △ABC ，∴a 2﹣3a ＝2或﹣a 2+3a ＝2，解得a 1＝（舍去），a 2＝，a 3＝1，a 4＝2， ∴E 1（，），E 2（1，﹣），E 3（2，﹣2）；（3）在y ＝ax 2+bx ﹣2中，当x ＝0时，y ＝﹣2，∴C （0，﹣2），∴OC ＝2，如图2，设P （0，m ），则PC ＝m +2，OA ＝3，AC ＝＝，①当PA ＝CA 时，则OP 1＝OC ＝2，∴P 1（0，2）；②当PC ＝CA ＝时，即m +2＝，∴m ＝﹣2， ∴P 2（0，﹣2）； ③当PC ＝PA 时，点P 在AC 的垂直平分线上，则△AOC ∽△P 3EC ，∴＝，∴P 3C ＝，∴m ＝， ∴P 3（0，），④当PC ＝CA ＝时，m ＝﹣2﹣，∴P 4（0，﹣2﹣）．综上所述，P点的坐标（0，2）或（0，﹣2）或（0，）或（0，﹣2﹣）．15．解：（1）由已知可求B（6，0），C（0，4），将点B（6，0），C（0，4）代入y＝﹣+bx+c，则有，解得，∴y＝﹣x2+x+4，令y＝0，则﹣x2+x+4＝0，解得x＝﹣1或x＝6，∴A（﹣1，0）；（2）∵点D在抛物线上，且横坐标为3，∴D（3，8），过点D作y轴的垂线交于点E，过点B作BF⊥DE交ED的延长线于点F；∴E（0，8），F（6，8），∴S△BCD ＝S梯形ECBF﹣S△CDE﹣S△BFD＝（EC+BF）×OB﹣×EC×ED﹣×DF×BF＝×（4+8）×6﹣×4×3﹣×3×8＝36﹣6﹣12＝18；（3）设P（m，﹣m2+m+4），∵PQ垂直于x轴，∴Q（m，0），且∠PQO＝90°，∵∠COB＝90°，∴点A、P、Q为顶点的三角形与△BOC相似有两种情况：①△PAQ∽△CBO时，＝＝，∴＝，解得m＝5或m＝﹣1，∵点P是直线BC上方的抛物线上，∴0≤m≤6，∴m＝5，∴P（5，4）；②△PAQ∽△BCO时，＝＝，∴＝，解得m＝﹣1或m＝，∵点P是直线BC上方的抛物线上，∴0≤m≤6，∴m＝，∴P（，）；综上所述：P（5，4）或P（，）时，点A、P、Q为顶点的三角形与△BOC相似．。

中考数学专题复习《二次函数中的面积问题》测试卷-附带参考答案学校:___________班级:___________姓名:___________考号:___________1．如图，在平面直角坐标系xOy 中，抛物线2y ax bx c =++与抛物线21y x x =-+-的形状相同，且与x 轴交于点()10-，和()40，．直线2y kx =+分别与x 轴 y 轴交于点A B 与2y ax bx c =++于点C D ，（点C 在点D 的左侧）．(1)求抛物线的解析式(2)点P 是直线2y kx =+上方抛物线上的任意一点 当2k =时 求PCD 面积的最大值(3)若抛物线2y ax bx c =++与线段AB 有公共点 结合函数图象请直接写出k 的取值范围．2．如图 直线3y x =-与x 轴交于点B 与y 轴交于点C 抛物线2y x bx c =++经过B C 两点 抛物线与x 轴负半轴交于点A ．(1)求抛物线的函数表达式(2)直接写出当23x x bx c ->++时 x 的取值范围(3)点P 是位于直线BC 下方抛物线上的一个动点 过点P 作PE BC ⊥于点E 连接OE ．求BOE △面积的最大值及此时点P 的坐标．3．如图 已知二次函数2y x bx c =-++的图象与直线3y x 相交于点A 和点B 点A 在x轴上 点B 在y 轴上 抛物线的顶点为P ．(1)求这个二次函数的解析式(2)在直线AB 下方的抛物线上是否存在点Q 使得2ABQ ABP S S =△△ 若存在 请求出点Q 的坐标 若不存在 请说明理由．4．如图 在平面直角坐标系中 已知点A 坐标为()2,4 直线2x =与x 轴相交于点B 连结OA 抛物线2y x 从点O 沿OA 方向平移 与直线2x =交于点P 顶点M 到A 点时停止移动．(1)求线段OA 所在直线的函数解析式(2)设抛物线顶点M 的横坐标为m 当m 为何值时 线段PB 最短(3)当线段PB 最短时 相应的抛物线上是否存在点Q 使QMA △的面积与PMA △的面积相等 若存在 请求出点Q 的坐标 若不存在 请说明理由．5．如图 二次函数243y ax x c -+＝的图象与x 轴交于点30A （，） 与y 轴交于点0,2B -（）．(1)求二次函数的解析式(2)若点P 为抛物线上一动点（直线AB 上方） 且4PBA S ＝ 求点P 的坐标．6．如图 已知抛物线23y ax bx =+-与x 轴的交点为()()4,0,2,0A D - 与y 轴交点为C ．(1)求该抛物线的解析式(2)设点C 关于抛物线对称轴的对称点为点B 在抛物线的A ~B 段上存在点P 求五边形APBCD 面积的最大值ax M S(3)问该抛物线上是否还存在与点P 不重合的点Q 使以A B C D Q 五点为顶点的凸五边形面积等于题（2）中五边形APBCD 面积的最大值ax M S 若存在 直接写出．．．．所有满足条件的点Q 的横坐标 若不存在 请说明理由．7．在平面直角坐标系中 点O 为坐标原点 抛物线23y ax bx =+-与x 轴分别交于点()1,0A - ()3,0B 与y 轴交于点C ．(1)求抛物线的表达式(2)如图 点D F 、分别是抛物线上第四象限 第二象限上的点 其中点F 的横坐标为t 连接BF 交y 轴于点E 连接DC DE 、 设CDE 的面积为s 且490s t += 求点D 的坐标．8．如图 二次函数223y mx mx =-++的图象与x 轴交于A B 两点（点A 在点B 的左侧） 与y 轴交于点C 顶点为D ．其对称轴与线段BC 交于点E 与x 轴交于点F ．连接ACBD 已知1tan 3ACO ∠=．(1)求m 的值(2)求CBD ∠的正切值(3)若点P 在线段BD 上 且FPB CAB ∠=∠ 请直接写出点P 的坐标．9．已知抛物线()()24y a x x =+-（a 为常数 且a<0）与x 轴交于A B ，两点（点A 在点B 的右侧） 与y 轴交于点C 经过点B 的直线12y x b =+与抛物线的另一交点为点D 与y 轴的交点为点E ．(1)如图1 若点D 的横坐标为3 试求抛物线的函数表达式(2)如图2 若DE BE = 试确定a 的值(3)如图3 在（1）的情形下 连接AC BC ， 点P 为抛物线在第一象限内的点 连接BP 交AC 于点Q 当APQ BCQ S S -△△取最大值时 试求点P 的坐标．10．已知：在平面直角坐标系中 O 为坐标原点 抛物线()2144y x h =--的顶点为A 与y 轴交于点B （点B 与点A 不重合） 点C 为y 轴右侧抛物线上异于点A 的一个动点 其坐标为(),m n ．(1)当91,4m n == 且点A 在第四象限时 求抛物线的解析式 (2)在（1）的条件下 连接AC 点P 为线段AC 下方抛物线上一点 连接,PA PC 当ACP △的面积最大时 求点P 的坐标(3)若m 满足方程260m m --= 作直线AC 与y 轴相交于点R ．当点B 在线段OR 上时 请利用图象法说明h 的取值范围．11．如图 已知直线3y x =-+与x 轴 y 轴分别交于A B 两点 抛物线2y x bx c =-++经过B 点 且与x 轴交于C D 两点（点C 在左侧） 且()3,0C -．(1)求抛物线的解析式(2)平移直线AB 使得平移后的直线与抛物线分别交于点D E 与y 轴交于点F 连接CE CF ， 求CEF △的面积．12．如图抛物线2y x bx c =++经过点()1,0A - 点()2,3B - 与y 轴交于点C 抛物线的顶点为D ．(1)求抛物线的解析式(2)抛物线上是否存在点p 使PBC 的面积是BCD △面积的3倍 若存在 请直接写出点p 的坐标 若不存在 请说明理由．13．如图 在平面直角坐标系中 抛物线239344y x x =--与y 轴交于点A 与x 轴的正半轴交于点B ．(1)求AOB 的面积(2)点P 是直线AB 下方抛物线上一点 过点P 作y 轴的平行线 交AB 于点E 过点P 作AB 的垂线 垂足为点F 求EF 的最大值及此时点P 的坐标(3)在抛物线上是否存在点Q 使OBQ BAO ∠=∠？若存在 请直接写出点Q 的坐标 若不存在 请说明理由．14．已知抛物线2y ax bx c =++与x 轴交于(1,0)A - (5,0)B 两点 C 为抛物线的顶点 抛物线的对称轴交x 轴于点D 连接AC BC 且4tan 3CBD ∠= 如图所示．(1)求抛物线的解析式(2)设P 是抛物线的对称轴上的一个动点．①过点P 作x 轴的平行线交线段BC 于点E 过点E 作EF PE ⊥交抛物线于点F 连接FB FC 求BCF △的面积的最大值①连接PB 求35PC PB +的最小值．15．如图 抛物线23y ax bx =+x 轴交于点A 和点()1,0B 与y 轴交于点C 连接AC经过点A 的一次函数()0y kx c k =+≠图象与抛物线的另一个交点为点53D ⎛ ⎝⎭点P 是抛物线上的一动点 连接AP CP ．(1)求抛物线23y ax bx =+ 并直接写出点A 的坐标(2)点P 在点A 和点C 之间运动 当APC △的面积最大时 求点P 的横坐标(3)若点P 位于y 轴左侧 过点P 作PE y ∥轴 交直线AD 于点E 当2PE OC =时求点P 的坐标．参考答案：1．(1)234y x x =-++(2)PCD 面积的最大值为278(3)k 的取值范围为02k <<或102k -<<2．(1)223y x x =--(2)03x << (3)7516 115,24⎛⎫- ⎪⎝⎭3．(1)223y x x =--+(2)存在 点Q 坐标为(4,5)--或(1,0)4．(1)2y x =(2)当1m =时 PB 最短(3)抛物线上存在点(12Q (22Q -使QMA △与APN 的面积相等．5．(1)224233y x x =-- (2)1043⎛⎫⎪⎝⎭，或(1,0)-6．(1)233384y x x =-- (2)9981±7．(1)2=23y x x --(2)点D 坐标为315,24⎛⎫- ⎪⎝⎭8．(1)1m = (2)13 (3)74,33P ⎛⎫⎪⎝⎭9．(1)2142y x x =-++ (2)14a =-(3)P 点的坐标为91,2⎛⎫⎪⎝⎭10．(1)()21644y x =-- (2)739,216P ⎛⎫⎪⎝⎭(3)34h <<或03h <<或4h <-11．(1)223y x x ；=--+(2)412．(1)2=23y x x --(2)存在 ()3,0或()1,0-13．(1)6(2)EF 最大值95 92,2P ⎛⎫- ⎪⎝⎭ (3)存在 25244,927⎛⎫- ⎪⎝⎭或7116,927⎛⎫- ⎪⎝⎭．14．(1)抛物线的解析式为241620999y x x =-++ (2)①BCF △的面积的最大值为32 ①35PC PB +的最小值为24515．(1)抛物线解析式为23233y =点A 的坐标为()3,0- (2)点P 的横坐标为32- (3)点P 的坐标为431,⎛- ⎝⎭或53⎛- ⎝⎭。