5.4平移导学案

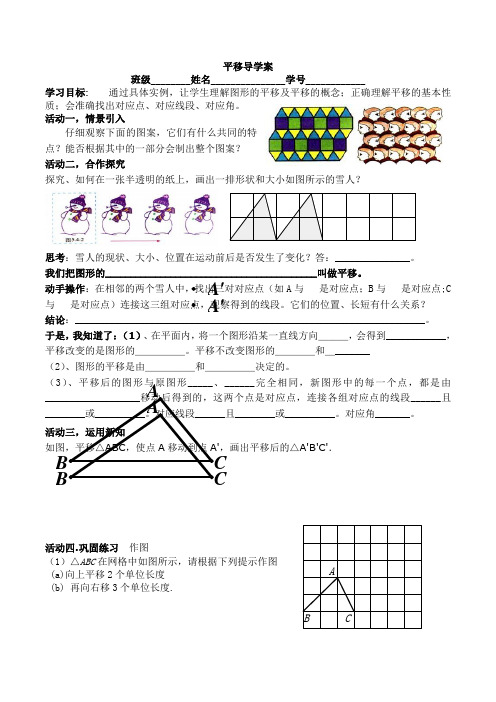
平移导学案班级________姓名_______________学号____________学习目标: 通过具体实例，让学生理解图形的平移及平移的概念；正确理解平移的基本性质；会准确找出对应点、对应线段、对应角。

活动一，情景引入仔细观察下面的图案，它们有什么共同的特点？能否根据其中的一部分会制出整个图案？活动二，合作探究探究、如何在一张半透明的纸上，画出一排形状和大小如图所示的雪人？思考：雪人的现状、大小、位置在运动前后是否发生了变化？答：_______________。

我们把图形的__________________________________________叫做平移。

动手操作：在相邻的两个雪人中，找出三对对应点（如A 与 是对应点；B 与 是对应点;C 与 是对应点）连接这三组对应点，观察得到的线段。

它们的位置、长短有什么关系？ 结论：______________________________________________________________________。

于是，我知道了：（1）、在平面内，将一个图形沿某一直线方向＿＿＿，会得到____________，平移改变的是图形的＿＿＿＿＿。

平移不改变图形的＿＿＿＿和＿_______（2）、图形的平移是由＿＿＿＿＿和＿＿＿＿＿决定的。

（3）、平移后的图形与原图形_____、______完全相同，新图形中的每一个点，都是由______且且________或__________。

对应角_______。

，画出平移后的△A'B'C'．A'A'活动四.巩固练习 作图（1）△ABC 在网格中如图所示，请根据下列提示作图(a)向上平移2个单位长度(b) 再向右移3个单位长度.A B C活动五.课外作业1、下列各组图形中，可以经过平移变换由一个图形得到另一个图形的是（ ）2、△ABC 沿BC 的方向平移到△DEF 的位置，（1）若∠B=260，∠F=740，则∠1=_____，∠2=____，∠A=_____，∠D=___。

《平移》导学案一、学习目标1、理解平移的概念，知道平移的基本性质。

2、能够识别平移现象，并能在方格纸上画出简单图形平移后的图形。

3、经历观察、操作、探究等数学活动，培养空间观念和推理能力。

二、学习重点1、平移的概念和性质。

2、画出简单图形平移后的图形。

三、学习难点1、理解平移的性质。

2、准确画出平移后的图形。

四、学习过程（一）情境导入同学们，在我们的生活中，有很多物体的运动都是平移现象。

比如，在笔直的公路上行驶的汽车、推拉窗户、电梯的升降等等。

那么，什么是平移呢？今天我们就来一起学习平移。

（二）知识探究1、平移的概念观察下面的图片，思考这些运动有什么共同特点？（展示图片：推拉窗户、电梯升降、抽屉的推拉）通过观察，我们可以发现这些运动都是沿着直线移动，并且移动过程中物体的形状、大小和方向都不发生改变。

像这样，在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动叫做平移。

平移不改变图形的形状和大小。

2、平移的性质（1）平移前后，对应点所连的线段平行（或在同一条直线上）且相等。

（2）平移前后，对应线段平行（或在同一条直线上）且相等。

（3）平移前后，对应角相等。

下面我们通过一个具体的例子来验证这些性质。

例：如图，三角形 ABC 经过平移得到三角形 A'B'C'，点 A、B、C 的对应点分别是 A'、B'、C'。

连接 AA'、BB'、CC'，你能发现什么？通过测量和比较，我们可以发现 AA'∥BB'∥CC'，且 AA'＝BB'＝CC'。

同时，AB∥A'B'，AB=A'B'，∠A=∠A'，∠B=∠B'，∠C=∠C'。

3、平移的作图（1）在方格纸上平移图形例：将方格纸上的三角形 ABC 向右平移 5 格。

步骤：①找出三角形 ABC 的关键点，如顶点 A、B、C。

2022-2023学年人教版七年级下册数学：5.4平移教案一、教学目标•了解平移的概念，明确平移的基本性质；•掌握平移的操作方法；•运用平移进行问题解决。

二、教学重点和难点教学重点•平移的定义；•平移的操作方法。

教学难点•运用平移解决实际问题。

三、教具准备•数学课本；•教学板书。

四、教学过程1. 导入与引入（5分钟）•引导学生回顾上节课的内容，复习“图形的对称性”。

•提问：在上节课中，我们学习了关于图形的哪些对称性？请举例说明。

2. 概念讲解（10分钟）•展示一个图形在平面上的移动，引出平移的概念。

•定义平移：平移是指一个图形在平面上按照给定方向和给定长度移动的过程。

3. 平移的基本性质（10分钟）•平移保持图形的大小、形状和方向不变。

•平移后，图形的每个点都按照相同的长度和方向进行移动。

4. 平移的操作方法（20分钟）•展示平移的基础操作方法，并与学生一起进行练习。

•使用教学板书进行演示。

5. 平移的练习（15分钟）•给定一个图形，要求学生进行平移操作，并画出平移后的图形。

•引导学生观察图形的特征，判断平移的方向和距离。

6. 运用平移解决问题（20分钟）•设计一些简单的问题，要求学生运用平移解决。

•引导学生理解平移在实际问题中的应用。

7. 总结与作业布置（5分钟）•和学生一起总结本节课的内容，并强调平移的基本概念和性质。

•布置作业：完成课堂练习题。

五、教学反思通过本节课的教学，学生对平移有了初步的了解，并能够运用平移解决简单的实际问题。

教学中注重培养学生的观察力和解决问题的能力，通过练习和应用，巩固了学生对平移的理解和掌握。

同时，教学过程中合理运用了多媒体教学手段，提高了教学效果。

需要注意的是，教师在引导学生进行练习和解题时，要注重学生的思维过程，引导学生分析问题并找到解决方法。

在布置作业时，要确保作业的难度适中，能够帮助学生进一步巩固所学知识。

《5.4 平移》导学案教材：P28——P30A.要点归纳，分点训练知识点1：平移的定义1、在平面内，将一个图形沿这样 移动 ，这样的图形运动，叫做平移变换，简称 。

2、平移过程中，发生变化的是 ，保持不变的是 。

3、平移的两个要素： 。

4、思考：物体的平移方向一定是水平的吗？知识点2：平移的性质1、思考：线段AA ’、线段BB ’和线段CC ’之间有什么样的位置关系？2、平移的性质：新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点叫 ，连接各组对应点的线段 （或在同一直线上）且 ，可简记为 知识点3：画平移图形 1、经过平移，三角形ABC 的顶点A 移动到了点D （如图所示），试画出平移后的三角形。

画平移图形的步骤：a 、 找出图形的关键点b 、 画出关键点的对应点C 、 连线知识点4：平移在解题中的应用1、如图，在一块长尾20m ，宽为8m 的长方形的草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是0.5m ）。

请你猜想草地的面积是多少。

A’ AA 与A’是对应点！B’ BC’ CA B C .DB.综合运用，能力提升1、快乐平移：4根火柴棒形成如图所示的“口”字,平移火柴棒后原图能变成的汉字是（ ）2、下列现象不属于平移的是( ) A.飞机起飞前在跑道上加速滑行 B.汽车在笔直的公路上行驶C.游乐场的过山车在翻筋斗D.起重机将重物由地面竖直吊起3、如图,△A ′B ′C ′是由△ABC 沿射线AC 方向平移2 cm 得到,若AC ＝3 cm,则A ′C ＝ __________4、如图，凯瑞酒店准备进行装修，把楼梯铺上地毯，已知楼梯的宽度是2米，楼梯的总长度为8米，总高度为6米，已知这种地毯每平方米的售价是60元.请你帮助酒店老板算下，购买地毯至少需要多少元？A B C D草地草地5、做一做： 请你拿出一张纸对折后，剪成两个相同的三角形，将两个三角形重合.试一试，如果其中一个三角形不动，怎样移动另一个三角形，得到下列图形，并体会哪些图形可以通过平移得到.《5.4平移》导学案答案A.要点归纳，分点训练知识点1：平移的定义1、在平面内，将一个图形沿这样某个方向移动一定的距离 ，这样的图形运动，叫做平移变换，简称平移 。

教师学科教案[ 20 – 20 学年度第__学期]任教学科：_____________任教年级：_____________任教老师：_____________xx市实验学校《5.4平移》教学设计四川省甘洛中学校罗艳【教材分析】1.教材内容“平移”是人教版教材数学七年级（下）第五章《相交线与平行线》的第四节。

本节内容分两课时，本节课是第一课时，主要学习平移的定义、性质、应用，第二课时继续学习平移的应用。

2.教材地位和作用图形的变换是义务教育阶段数学课程标准中“空间与图形”领域的一个主要内容，它努力体现运动变换的理念与思想，是新教材与传统教材有较大差别的地方。

平移是本套教材中引进的第一个图形变换。

教科书将“平移”安排在本章最后一节，一方面是考虑将其作为平行线的一个应用，另一方面考虑引入平移变换，可以尽早渗透图形变换的思想。

图形变换除了平移、对称和旋转这三种基本变换外，还有相似图形中的位似变换，以及在直角坐标系中用代数手段来研究的图形变换。

初中阶段的图形变换主要从定性的角度让学生去感悟，而对于它的定量讨论主要放在高中阶段的向量、解析几何及矩阵等有关章节中去完成。

平移如同旋转、对称一样，是一种保形变换，它是现实生活中广泛存在的现象，是现实世界运动变化的最简捷形式之一。

它不仅是探索图形的一些性质的必要手段，而且也是解决实际生活中的具体问题以及进行数学交流的重要工具。

人教版教材数学七年级（下）第五章第四节第一课时。

【学情分析】本班学生只是掌握了图形的初步认识，初次接触图形的变换。

加上大部分学生是来自全县各个乡镇的少数民族，不善于表达自己的观点，且基础知识相对较差。

因此，需要教师在教学中尽量营造宽松的氛围，引导学生合作探索、归纳总结，再利用多媒体形象直观的特点展现图形运动变换的过程，帮助学生理解、消化、吸收新知。

【教学目标】1、知识与技能⑴．认识图形的平移变换，明确其特征，理解“平移不改变图形的形状与大小”以及“对应点所连的线段平行且相等”等基本性质。

1、观察思考：观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?
2、探索活动：
如何在一张半透明的纸上，画出一排形状和大小如图的雪人？
3、思考：在所画的相邻的两个图案中，找出三组对应点，连接它们，观察它们的位置、长短有什么关系？
＿＿，对应角
＿＿＿＿，对应点所连的线
段＿＿＿＿。

（二）平移作图
如图,平移三角形ABC,使点A 运动到A`,画出平
移后的三角形A`B`C`.
B
A
___________；数量关系是___________
2.如图，将△ABC 平移到△A'B'C'的位置.填写下列各对应元素点C 的对应点是点，线段BC 的对应线段是线段线段CA 的对应线段是线段
,∠B 的对应角是∠，∠C
3．如图，四边形ABCD 中，AD ∥BC,且AD ＜BC ，△ABC 平移到△DEF 的位置．⑴指出平移的方向和平移的距离；⑵试说明AD+BC=BF ．
5．4第1、2、3题．5．4第4、5、6题．
平移不改变图形的形状和大小平移不改变直线的方向
一个图形和它经过平移后所得的图形中，两组对应点的连线平行（或在同一直线上）且相等
本节课通过生活中的实例引入平移的概念，在学习中，引导学生分析、并通过例题和练习加深对平移性质的理解．让学生作图，自主探究．平移的作图是本节课的重点，应让学生加强训练，结合解题中的错误分析原因，举一反三
A D
B E C
F。

《5.4平移》导学案
一、学习目标：
1.了解平移的概念,会进行点的平移.
2.理解平移的性质,能解决简单的平移问题.
二、自主学习：(平移的定义)
你知道这几幅图案中运动的现象有什么共同的特点吗?
1.问题:如何在一张纸上画出一排和课本P28图5.42形状、大小都一样的雪人,你画的雪人和课本上的一样吗?你是怎么画的?
2.在课本P28图5.44中,雪人的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?
3.请你连接对应点,观察得到的线段,它们有什么关系?
4.下面②③④⑤四幅图中哪幅图是由①平移得到的?
(1) (2)
(3)
三、合作探究：（平移的性质）
1.平移线段AB,使点A移动到点A'.画出平移后的线段A'B'.
2.经过平移,△ABC的顶点A移到了点D.画出平移后的三角形.
3.如图,△ABE沿射线XY的方向平移一定距离后成为△CDF.找出图中三条平行且相
等的线段.
四、达标测评：（测评习题）
1.如图,△EFG是将△ABC向右平移一定距离而得.试找出图中平行且相等的线段.
2.如图∠ABC是∠O经过平移而得的角,若∠O=65°,则∠ABC等于多少度?
3.在下面的七幅图案中,②③④⑤⑥⑦中的哪个图案可以通过平移图案①得到?
五、
六、
七、
八、
4.由△ABC平移而得的三角形共有多少个?
5.能由△AOB平移而得的图形是哪几个?。

【学法指导】平移是一种基本的图形变换，是教材引入的第一个图形变换（今后还有图形的轴对称、图形的旋转、图形的相似等）。

首先，观察几个图案，分析这些图案的共同特点，找出几个生活中利用平移得到的图案，感受平移现象与生活的密切联系。

接着通过探究栏目的动手活动为思考栏目的观察分析提供准备，最后通过归纳栏目对平移变换的基本特征进行全面概括，并在此基础上给出平移变换的概念。

对于平移变换除了有水平方向的平移外，还有其他方向的平移，学习中要注意体会。

【学习过程】【侯课朗读】教材第27-29页一、学前准备1．生活中有许多美丽的图案，他们都有着共同的特点，请同学们欣赏课本27页图案。

观察上面图形，我们发现他们都有一个局部和其他部分重复，如果给你一个局部，你能复制他们吗？请你试一试。

2．请将图中的“小鱼”向左平移5格。

二、解读教材探究一：请同学们仔细阅读课本P27～28页，你能发现并归纳平移的特征吗？平移的特征：(1)把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小；(2)新图形中的每一点，都是由原图形中的某一个点移动后得到的，这两个点是；(3)连接各组对应点的线段平行（或在同一条直线上）且。

即，在平面内，将一个图形沿移动一定的，图形的这种移动，叫做平移变换，简称平移。

注意：图形平移的方向，不一定是水平的，图形经过平移后，_______图形的位置，________图形的形状，________图形的大小。

(填“改变”或“不改变”)练习一：1．几何图形经过平移，图形中对应点所连的线段平行（或在同一条直线上）且，对应线段且，对应角。

2．平移改变的是图形的（）A．位置 B．形状 C．大小 D．位置、形状、大小3．下列现象中，不属于平移的是（）A．滑雪运动员在的平坦雪地上滑行 B．大楼上上下下地迎送来客的电梯C．钟摆的摆动 D．火车在笔直的铁轨上飞驰而过4．下列各组图形，可经平移变换由一个图形得到另一个图形的是（）探究二：你能按要求将图形平移吗？动手试一试。

（3）在相邻的两个雪人中，找出三组对应点（如：鼻
尖A 与A ′,帽顶B 与B ′,纽扣C 与C ′）,连接这些对应
点，观察得出的线段，他们的位置、长短有什么关系？
归纳：新图形中的每一点都是由原图形中的某一点移动
后得到的，这两个点是________。

连接各组对应点的线段
________且________。

A' C'
B' A C B
3、图中线段____可以由线段b平移得到，先向___(或向___)平移____格（或____格），再向___（或向___）．平移____格（或____格）。

4、如图7所示，在网格中，有三角形ABC，将A点平移到P点，
画出三角形ABC平移后的图形．
（1）将A点向_____（或向_____）平移_____格（或_____格）．
（2）再向____（或向___）平移____格（或____格），得点P．
（3）同理B，C与A点平移次数方向距离一样，易得B′，C′．
（4）连结PB′，PC′，B′C′得到三角形ABC平移后的三角形PB′C′．。