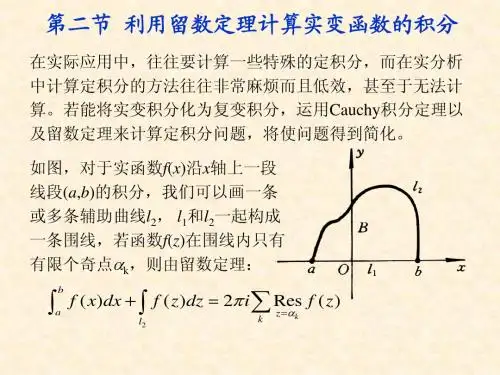
用留数定理计算实积分
- 格式:ppt
- 大小:5.33 MB
- 文档页数:34








解析延拓246224611...(||1)1()1...(||1)||1()b z z z z zf z z z z z z f z -+-+=<+=-+-+<<↓是幂级数,在单位圆内部收敛,其和是解析函数,但在单位圆外级数发散而没有意义。
在一较小的区域上为解析函数21()1b B F z z i =+±↓在除去z=的全平面上是解析函数。
在含区域的一个较大的区域上是解析函数22|z|<1b 1F(z)f(z)1z +...(|z|<1)1z两者在较小的区域()上等同称=是=-的+解析延拓b ()F(z)Bb ().f z f z ⇒解析延拓:已给某个区域上的解析函数找出另一函数,在含有区域b 的一个较大区域上为解析函数,且在区域上等同于即解析函数定义域的扩大bB4.2 利用留数定理计算实变函数定积分留数定理的一个重要应用是计算某些实变函数的定积分。
实变函数的定义域在实轴上,而运用留数定理时需要寻找一个回路,显然在计算此类积分时需要构造一些回路。
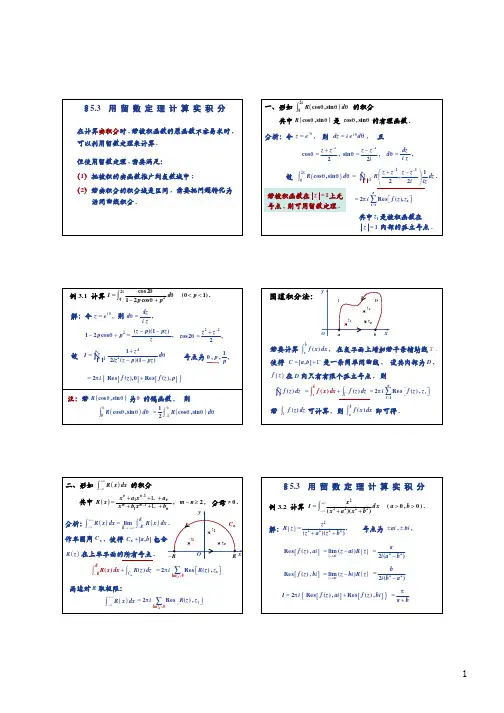
教学重点:介绍三类实变函数定积分的计算().baf x dx a b l →⎰1积分区间[,],可看作复平面上的实轴上的一段xyo l 2121212(1)(2)B ()B (z)()()()ll l l l l l l l l f x f f z dz f x dx f z dz→−−−−→=+⎰⎰⎰ 解析延拓构造回路方法:利用自变数变换将复平面上某个新的回路补一段曲线,使+=回路,包围区域,则上的闭上的↓↓↓利用留数待求积分较易算出的积分定理计算 一般为0或用待求 积分表示bal 1B20(co i ,s ,s n )R x x dx ππ⎰类型一:特点:被积函数为三角函数的有理式积分区间[0,2],:0~2,11()ix ix ixixz e x z e z z dz dz d e ie dx dx izπ===−−−−−→===∴=绕原点一周回到方法:作变数代换:令则从xyo2πl 11111||11111cos (),sin ()2222I=(,)2Re (),221()(,)22ix ix ix ixk z e e e e x z z x z z i iz z z z dzR i sf z i iz z z z z f z R iz iπ------=--+-==+==-→+-=+-=⎰ 则实变函数定积分复变函数回路积分则原积分2012||1||1I=(01)1cos ,/()2212ixz z dx x dz z e dx iz dz iz dzI z z i z z πεεεεε-==<<+==∴==++++⎰⎰⎰ 例1:解:令则1122122221,21121122||122(1)()()244111112()111Res '()2222212222Re ()21z z z z z z z z z z z z z z z z f z z z z dz I i sf z i z z i εεεεεεεεεεεεϕψεεεππεεε===++++=---±--±-==-±-=∴===++-∴===++-⎰ 令=在|z|=1内只有一个奇点,且为单极点()=2212221111|1(1)(1)111111|1z z εεεεεεεεεεεε-+---==---<=---+-==>>且||2022022222002I=(0)cos 2(01)1cos 11122()cos (1cos )1dxa a x dx x dx dx a x a a a x a aππππεεπεεεππεεεε>>+=<<+-∴===+-+-⎰⎰⎰⎰例:解:由可作为公式来用20220222023322222222233220022222I=(1)cos (01)1cos 2cos 1222(cos )2()()221(cos )1cos ()(1)dxa a x dx x dx a a x a dx aa a x a a dxadxa a x x a ππππππεεπεεππεεεππεεεε>+<<+=+--=-=-+--===++--⎰⎰⎰⎰⎰⎰例:例:()解:在基础上两端对求微分再令,()2201122||1||1||12||1||11I=(01)12cos 1,,cos ()22/()()122,()(1)()(1),ix ixixz z z z z dxx dz e e z e dx x z z iz dz iz idz idzI z z z z z z z z idz idzz z z z z πεεεεεεεεεεεεεεεε---=====<<-++====+--∴===+--+----+-==----∴=⎰⎰⎰⎰⎰⎰ 例:计算解:令则211212||11||1Res ()lim()()(1)12I=2Res ()()(1)1z z z z z i if z z z z idz i f z z z εεεεεεεεππεεε→====∴==----==---⎰ 是被积函数的两个单极点,但在内只有一个极点。
