6个标准差

六西格玛的含义六西格玛管理，作为一套以实现产品零缺陷为目标的科学管理体系，正逐渐成为企业管理的重要工具。

那么，究竟什么是六西格玛管理呢？关于6σ“σ”是一个希腊字母，中文读作“西格玛”，英文读作”sigma”。

在统计学中，常常用它来指代标准差。

通俗来说，就是表示数据的波动程度。

因此，“6σ”就是表示6个标准差。

那么6个标准差代表什么呢？这里要引入一个“正态分布”的概念，英文为”Norm distribution”, 也叫“标准分布”。

从这个叫法可以看出，它是自然界中最为常见的一种分布形式。

这种分布通常遵循以下规律：中间多，两边少。

即大多数的数据会集中在平均值附近，越远离均值，数据越少。

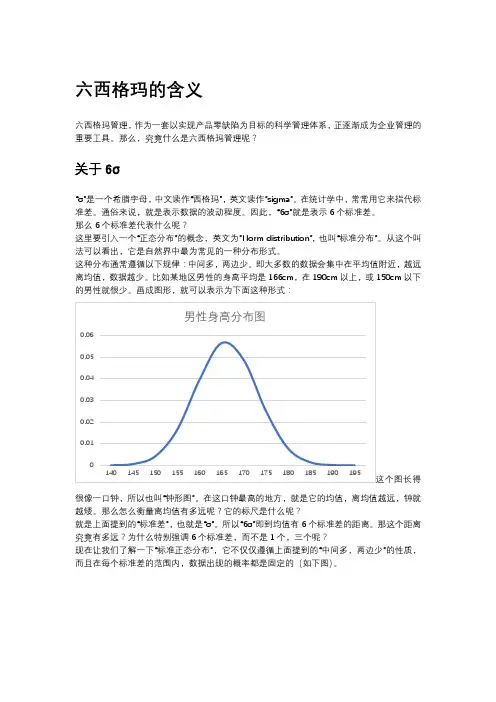
比如某地区男性的身高平均是166cm，在190cm以上，或150cm以下的男性就很少。

画成图形，就可以表示为下面这种形式：很像一口钟，所以也叫“钟形图”。

在这口钟最高的地方，就是它的均值，离均值越远，钟就越矮。

那么怎么衡量离均值有多远呢？它的标尺是什么呢？就是上面提到的“标准差”，也就是“σ”。

所以“6σ”即到均值有6个标准差的距离。

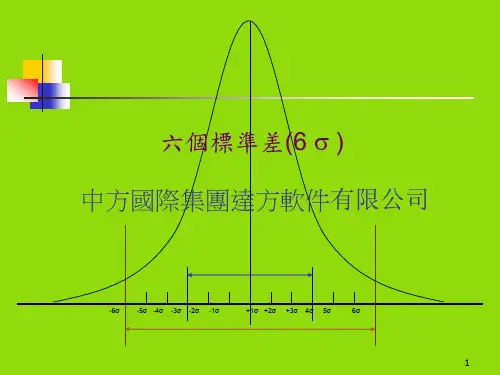
那这个距离究竟有多远？为什么特别强调6个标准差，而不是1个，三个呢？现在让我们了解一下“标准正态分布”，它不仅仅遵循上面提到的“中间多，两边少”的性质，而且在每个标准差的范围内，数据出现的概率都是固定的（如下图）。

这个图上只画出了+/-3σ距离内的概率，+/-6σ范围内的概率是99.9997%。

我们知道99.999%的黄金基本就是其纯度的极限了，那么在制造领域中，+/-6σ就意味着，99.9997%的产品是合格的。

它的百万机会缺陷率是3.4。

也就是说，在一百万次可能出现缺陷的机会中，只有3.4次会出问题。

可以说，它在统计意义上，量化了“零缺陷”的概念。

正态分布作为自然界中最常见的分布形式，为理解和应用六西格玛管理提供了重要的理论基础。

六西格玛管理与6σ现在，我们知道”6σ”就是代表零缺陷，那么六西格玛管理便是使产品实现零缺陷的一整套系统。

六西格玛随着实践的经验积累，它已经从单纯的一个流程优化概念，衍生成为一种管理哲学思想。

它不仅仅是一个衡量业务流程能力的标准，不仅仅是一套业务流程不断优化的方法，进而成为一种应对动态的竞争环境，提升企业竞争力，取得长期成功的企业战略。

由来六西格玛（Six Sigma）是在20世纪90年代中期开始被GE从一种全面质量管理方法演变成为一个高度有效的企业流程设计、改善和优化的技术，并提供了一系列同等地适用于设计、生产和服务的新产品开发工具。

继而与GE的全球化、服务化、电子商务等战略齐头并进，成为全世界上追求管理卓越性的企业最为重要的战略举措。

六西格玛逐步发展成为以顾客为主体来确定企业战略目标和产品开发设计的标尺，追求持续进步的一种管理哲学。

6σ质量管理方法6σ管理法是一种统计评估法，核心是追求零缺陷生产，防范产品责任风险，降低成本，提高生产率和市场占有率，提高顾客满意度和忠诚度。

6σ管理既着眼于产品、服务质量，又关注过程的改进。

“σ”是希腊文的一个字母，在统计学上用来表示标准偏差值，用以描述总体中的个体离均值的偏离程度，测量出的σ表征着诸如单位缺陷、百万缺陷或错误的概率性，σ值越大，缺陷或错误就越少。

6σ是一个目标，这个质量水平意味的是所有的过程和结果中，99.99966% 是无缺陷的，也就是说，做100万件事情，其中只有3.4件是有缺陷的，这几乎趋近到人类能够达到的最为完美的境界。

6σ管理关注过程，特别是企业为市场和顾客提供价值的核心过程。

因为过程能力用σ来度量后，σ越大，过程的波动越小，过程以最低的成本损失、最短的时间周期、满足顾客要求的能力就越强。

6σ理论认为，大多数企业在3σ～4σ间运转，也就是说每百万次操作失误在6210～66800之间，这些缺陷要求经营者以销售额在15%～30%的资金进行事后的弥补或修正，而如果做到6σ，事后弥补的资金将降低到约为销售额的5%。

为了达到6σ，首先要制定标准，在管理中随时跟踪考核操作与标准的偏差，不断改进，最终达到6σ。

什么是6西格玛什么是6西格玛是希腊文的字母，是用来衡量一个总数里标准误差的统计单位。

一般企业的瑕疵率大约是3到4个西格玛，以4西格玛而言，相当于每一百万个机会里，有6210次误差。

如果企业不断追求品质改进，达到6西格玛的程度，绩效就几近于完美地达成顾客要求，在一百万个机会里，只找得出3.4个瑕疪。

6西格玛（6Sigma）是在九十年代中期开始从一种全面质量管理方法演变成为一个高度有效的企业流程设计、改善和优化技术，并提供了一系列同等地适用于设计、生产和服务的新产品开发工具。

继而与全球化、产品服务、电子商务等战略齐头并进，成为全世界上追求管理卓越性的企业最为重要的战略举措。

6西格玛逐步发展成为以顾客为主体来确定企业战略目标和产品开发设计的标尺，追求持续进步的一种质量管理哲学。

6西格玛的主要原则在推动6西格玛时，企业要真正能够获得巨大成效，必须把6西格玛当成一种管理哲学。

这个哲学里，有六个重要主旨，每项主旨背后都有很多工具和方法来支持：1.真诚关心顾客。

6西格玛把顾客放在第一位。

例如在衡量部门或员工绩效时，必须站在顾客的角度思考。

先了解顾客的需求是什么，再针对这些需求来设定企业目标，衡量绩效。

2. 根据资料和事实管理。

近年来，虽然知识管理渐渐受到重视，但是大多数企业仍然根据意见和假设来作决策。

6西格玛的首要规则便是厘清，要评定绩效，究竟应该要做哪些衡量(measurement)，然后再运用资料和分析，了解公司表现距离目标有多少差距。

3. 以流程为重。

无论是设计产品，或提升顾客满意，6西格玛都把流程当作是通往成功的交通工具，是一种提供顾客价值与竞争优势的方法。

4.主动管理。

企业必须时常主动去做那些一般公司常忽略的事情，例如设定远大的目标，并不断检讨；设定明确的优先事项；强调防范而不是救火；常质疑「为什么要这么做」，而不是常说「我们都是这么做的。

」5. 协力合作无界限。

改进公司内部各部门之间、公司和供货商之间、公司和顾客间的合作关系，可以为企业带来巨大的商机。

通常，计算标准偏差有四个步骤：计算平均值，计算方差，计算平均方差和计算标准差。

例如，对于一组六个数字2、3、4、5、6、8，可以通过以下步骤计算标准偏差：计算平均值：（2 + 3 + 4 + 5+ 6 + 8）/ 6 = 30/6 = 5计算方差（2 – 5）^ 2 =（-3）^ 2 = 9（3 – 5）^ 2 =（-2）^ 2 = 4（4 – 5）^ 2 =（-1）^ 2 = 0（5 – 5）^ 2 = 0 ^ 2 = 0（6 – 5）^ 2 = 1 ^ 2 = 1（8 – 5）^ 2 = 3 ^ 2 = 9计算出平均方差（9 + 4 + 0 + 0 + 1 + 9）/ 6 = 24/6 = 4计算标准偏差：√4= 2标准差是概率统计中最常用的统计离散度度量。

标准偏差定义为方差的算术平方根，它反映组中个体之间的分散程度。

原则上，按分布程度测量的结果具有两个属性：总量或随机变量的标准偏差以及子集中样本数量的标准偏差。

公式如下。

标准偏差的概念由卡尔·皮尔森（Karl Pearson）引入统计学中。

洋葱备注：所有数字减去其平均值的平方和，然后将结果除以数字组的数量（或数字减去1，即变数），然后打开获得的值的根和获得的数字是这组数据的标准差方差=（x1-x）^ 2 +（x2-x）^ 2 +（x3-x）^ 2 + ... +（xn-x）^ 2= X1 ^ 2 + X2 ^ 2 + X3 ^ 2 + ...... + Xn ^ 2-2x（X1 + X2 + X3 +…+ Xn）+ n X ^ 2（其中x 1，X2，X3，xn是每个项目的编号，X是平均值）（n）根的标准偏差。

六标准差的原理1. 引言六标准差是一种用于评估过程稳定性和能力的统计方法。

通过计算数据的六倍标准差，我们可以得到一个量化的指标，用于判断一个过程的性能是否可接受。

本文将介绍六标准差的原理及其在质量管理中的应用。

2. 基本概念在介绍六标准差之前，我们先来了解一些基本概念。

•标准差（Standard Deviation）：标准差是描述一组数据的离散程度的统计指标。

它表示数据点与平均值之间的平均偏离程度。

标准差越大，数据的离散程度就越高。

•正态分布（Normal Distribution）：正态分布又称为高斯分布，是一种常见的概率分布模型。

正态分布的特点是均值位于数据的中心，数据点的离散程度逐渐减小，符合“钟形曲线”的分布特点。

3. 六标准差的计算公式六标准差的计算公式如下：六标准差 = 6 * 标准差通过将标准差乘以6，我们可以得到一个量化的指标，用于衡量一个过程的稳定性和能力。

如果六标准差的值较小，说明过程的稳定性较高，数据点的离散程度较小；反之，如果六标准差的值较大，说明过程的稳定性较差，数据点的离散程度较大。

4. 六标准差的应用4.1 过程稳定性评估六标准差可以用于评估一个过程的稳定性。

传统上，当一个过程的六标准差值小于1.5时，被认为是一个稳定的过程。

这意味着过程的性能相对稳定，数据点的离散程度较小，符合预期。

4.2 过程能力评估除了过程稳定性评估，六标准差还可以用于评估一个过程的能力。

过程能力是指过程在宽容度范围内生产出合格产品的能力。

六标准差可以帮助我们判断过程是否达到了内部和外部客户的要求。

一般来说，当一个过程的六标准差值小于3时，被认为是一个能力良好的过程。

这意味着过程能够控制在合理的界限内，生产出高质量的产品。

5. 注意事项在应用六标准差时，需要注意以下几点：•六标准差是一种相对粗略的评估方法，不能代替其他更精确的统计方法。

•六标准差适用于连续型数据。

如果数据是离散型的，需要采用其他适当的方法。

六西格玛计算公式1.平均值（μ）：数据集的所有观察值的平均值。

2.标准差（σ）：数据集的所有观察值与平均值之间的平均差异。

3.右侧六西格玛（+6σ）：在正态分布曲线上右侧的第六个标准差之外的区域，其发生概率非常低。

4.左侧六西格玛（-6σ）：在正态分布曲线上左侧的第六个标准差之外的区域，其发生概率非常低。

下面是六西格玛计算公式的具体步骤：1.收集数据：收集与流程或问题相关的数据。

2.计算平均值（μ）：将所有数据项相加，然后除以观察值的总数。

3.计算标准差（σ）：计算每个数据与平均值之间的差异，然后将所有差值的平方相加，最后除以观察值的总数。

然后取平方根，得到标准差。

4.计算右侧六西格玛（+6σ）：将平均值与六个标准差相加。

5.计算左侧六西格玛（-6σ）：将平均值与六个标准差相减。

六西格玛计算公式的应用常见于质量管理和业务流程改进领域，它可以帮助组织识别并减少过程中的变异性，并提高产品和服务的质量和可靠性。

例如，一个制造公司可以使用六西格玛计算公式来确定生产线上的过程是否稳定，并采取适当的措施来减少产品的次品率。

需要注意的是，六西格玛计算公式是一种理论模型，它假设数据符合正态分布，并且所有观察值都是独立的。

在实际应用中，数据的分布可能会偏离正态分布，或者数据之间可能存在相互关联的关系。

因此，在使用和解释六西格玛计算公式时，需要结合实际情况进行综合分析，并考虑其他因素的影响。

六西格玛计算公式是一种强大的工具，可以帮助组织实现持续改进和优化。

通过对数据的分析和应用六西格玛计算公式，组织可以更好地了解和掌握其过程的性能，从而优化流程、提高质量、降低成本，并为持续发展提供支持。

标准差怎么算例题
计算标准差的步骤通常有四步：
计算平均值、计算方差、计算平均方差、计算标准差。

例如，对于一个有六个数的数集2,3,4,5,6,8，其标准差可通过以下步骤计算：
1、计算平均值：
(2+3+4+5+6+8)、6=30、6=5
2、计算方差：
(2–5)^2=(-3)^2=9
(3–5)^2=(-2)^2=4(
4–5)^2=(-1)^2=0
(5–5)^2=0^2=0
(6–5)^2=1^2=1
(8–5)^2=3^2=9
3、计算平均方差：
(9+4+0+0+1+9)、6=24、6=4
4、计算标准差：
√4=2
标准差（Standard Deviation），在概率统计中最常使用作为统计分布程度（tatitical diperion）上的测量。

标准差定义为方差的算术平方根，反映组内个体间的离散程度。

测量到分布程度的结果，原则上具有两种性质：一个总量的标准差或一个随机变量的标准差，及一个子集合样品数的标准差之间，有所差别。

其公式如下所列。

标准差的观念是由卡尔·皮尔逊（Karl Pearon）引入到统计中。

例子：
1,2,3,4,5,6,7,8,9
均值为5
每个数字减去均值
-4,-3,-2,-1,0,1,2,3,4
平方
16,9,4,1,0,1,4,9,16
求和
16+9+4+1+0+1+4+9+16=60
一共有9项,所以（最重要的一步）
60、（9-1）=7。

5
标准差就是根号7。

5。