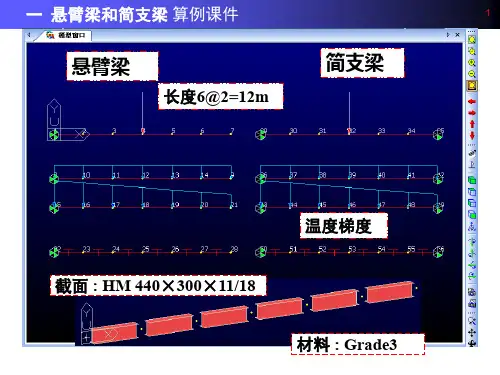
悬臂梁、简支梁立柱

单元幕墙常见三种立柱受力连接方式论文摘要：在采用双支座连续梁时，a/L≤0.10，其材料及安装成本最高；随着a/L的值增大，其材料及安装成本相应降低。

所以如果条件允许，我们在实际工程中尽可能将短跨之间的间距调大，以达到节省成本的效果。

引言：随着建筑技术的不断发展与创新，对建筑幕墙的要求也越来越高，在结构安全的情况下要做到经济，美观还要施工方便，单元式幕墙因为安装方便，现场安装工作较少，在现幕墙中应用非常广泛，单元式幕墙结构安全、经济合理越来越重要；现在我们选取在单元幕墙中最常见的立柱构造和连接形式，分析其结构受力和经济性能。

一单元式幕墙立柱常用的力学模型实际工程中，幕墙立柱的连接形式及力学模型，最常见的有以下三种：单跨悬臂梁、简支梁（如下图中“附图（一）”所示），双跨连续梁（如下图中“附图（二）”所示）。

然而究竟采用哪一种受力合理，且经济实惠便于安装呢？本文通过一个实际工程进行详细的分析。

三计算实例比较某单元式幕墙工程， 50年一遇的基本风压为： 0.55Kpa，工程最高高度106m，地面粗糙度类型C类，设防烈度为7度，地震加速度为0.10g，水平地震影响系数最大值为0.08；层高4200mm，立柱的分格为1500mm，双支座连续梁时短跨长度为：a=420mm，长跨为：b=3780mm；单跨悬臂梁时，悬挑跨长为：a= 420mm；此时a/L=0.10；另外在双支座连续梁时，取a/L=0.20，短跨长度a=840mm，做为参考比较。

在保持单元立柱总宽度及形状不变的前提下，仅改变单元立柱的高度，使其能够在受荷载作用时，强度和挠度均能满足规范要求。

通过单元立柱所对应的截面见下图：附图三所示。

三结论对于单元幕墙，采用相类似的立柱（本文中所指为：立柱的截面宽度相同，除截面高度不同外形状相同）与支座连接形式时，立柱采用简支梁，单跨悬臂梁，双跨连续梁这三种连接方式时：（注：a/L中a指的是短跨或悬臂的长度，L指的是杆件的总长度。

《桥梁工程》第二篇秋华整理第二篇1）混凝土梁桥优点:造价低、耐久性好、适应性强、刚度大、整体性好、便于工业化施工。

缺点:自重大、钢筋混凝土梁常带裂缝工作。

2）混凝土梁桥分为：简支梁（板）桥、连续梁（板）桥、悬臂梁（板）桥。

3）板桥优点：建筑高度小，外形简单、施工方便，便于整体现浇和预制装配，预制装配质量小，架设方便。

缺点：自重大，跨径不宜过大，适合于小跨径桥梁。

4）简支梁特点：施工方便、静定体系对地基要求不高、跨中正弯矩最大、适合于小跨径桥梁。

5）悬臂梁桥特点：单悬臂、双悬臂，卸载弯矩使跨中弯矩大大减小，静定体系对地基要求不高，跨中有接缝、行车条件不好，跨中的牛腿、伸缩缝、易损坏，适合于中等以上跨径桥梁，施工不方便。

6）连续梁桥特点：恒载、活载均有卸载弯矩，无伸缩缝、行车条件好，超静定体系对地基要求高，存在临时固结和体系转换问题，适合于中等以上跨径桥梁。

7）T形刚构桥特点：卸载弯矩类似于悬臂梁，适合于悬臂施工、节省大吨位支座，其中的静定体系对地基要求不高，跨中的牛腿、伸缩缝，易损坏，行车条件不好，适合于中等以上跨径桥梁。

8）连续刚构桥特点：综合连续梁与T构的优点，跨中正弯矩较连续梁要小而可降低跨中区域的梁高，超静定体系对地基承载了要求高，会产生较大的温度次内力，梁墩联结处应力复杂，适合于中等以上跨径的高墩桥梁9）按施工方法分类整体浇筑式梁桥：整体性好预制装配式梁桥：施工方便，大量节省支架模板，不受季节性影响等优点顶推法施工；悬臂施工；转体施工。

10）钢筋混凝土和预应力混凝土梁桥常用的分块方式有：纵向竖缝划分、纵向水平缝划分、纵横向竖缝划分。

11）装配式梁桥预制拼装单元的划分－直接影响到结构受力、构件预制、运输和安装以及拼装接头的施工等问题，也与所选用的横截面型式紧密相关。

块件划分的一般原则：a)考虑运输工具和装吊设备的承载能力，装载限界的要求；b)构造应当简单，并且尽可能少用接头。

c)块件形状和尺寸应力求标准化。

桥梁的基本体系桥梁的基本体系按结构体系及受力特点，桥梁可划分为梁、拱、索三种基本体系，以及由基本体系之间组合而形成的组合体系1．梁式桥梁式桥的特点是其桥跨的承载结构由梁组成。

在竖向荷载作用下梁的支承处仅产生竖向反力而无水平反力（推力）。

梁的内力以弯矩和剪力为主。

梁式桥可分为简支梁桥，连续梁桥和悬臂梁桥。

简支梁桥的跨越能力有限（一般在50m以下），当计算跨径小于25m时，通常采用混凝土材料，而计算跨径大于25m时，更多采用预应力混凝土材料。

2．拱式桥拱式桥的主要承重结构是拱圈或拱肋。

其特点是结构在竖向荷载作用下，两拱脚处不仅产生竖向反力，还产生水平力（推力），由于水平推力的作用使拱中的弯矩和剪力大大地降低。

设计合理的拱主要承受拱轴压力，拱截面内弯矩和剪力均较小，因此可充分利用石料或混凝土等抗压能力强而抗拉能力差的圬工材料。

拱式桥是推力结构，其墩台，基础必须承受强大的拱脚推力。

因此拱式桥对地基要求很高，适建于地质和地基条件良好的桥址。

拱式桥构造简单，承载能力大，造型美观，是桥梁工程中广泛采用的桥型之一。

3．悬索桥悬索桥又称吊桥，其特点是桥梁的主要承重结构由桥塔和悬挂在塔上的高强度柔性缆索及吊索，加劲梁和锚锭结构组成。

桥跨上的荷载由加劲梁承受，并通过吊索将其传至缆索。

主缆索是主要承重结构，但其仅受拉力。

缆索本身是几何可变体，但可通过桥塔，锚锭结构及作用的荷载相组合，在空间形成有一定几何形状的平衡受力结构体系。

主缆索的拉力通过对桥塔的压力和锚锭结构的拉力传至基础和地基。

这种桥型充分发挥了高强钢缆的抗拉性能，使其结构自重较轻，能以较小的建筑高度跨越其他任何桥型无法比拟的特大跨度。

4．组合体系组合体系桥是指承重结构采用两种基本结构体系，或一种基本体系与某些构件（塔，柱，索等）组合在一起的桥。

代表性的组合体系有以下几种。

（1）刚架桥刚架桥是梁与立柱（墩柱、竖墙）刚性连接的结构体系。

刚架桥的特点是在竖向荷载作用下，柱脚处不仅产生竖向反力，同时产生水平反力，使其基础承受较大推力。

引入 新课 练习 小结
《建筑力学》课件
————计算简单梁在集中荷载作 用下的支座反力
大庆市建设中等职业技术学校
作业
李福占
一、引入
1、建筑工程中常见 的简单梁 1）、简支梁 2）、悬臂梁 3）、伸臂梁（下 一讲内容）
2、集中荷载：
指荷载作用在结构上的面积与结构尺 寸相比很小。常见的是在梁上立柱（结构 柱，施工模板下硬支撑）且荷载方向是垂 直于梁轴线、向下。
MA=P×3= 10×3=30KN· M(方向同图示) 3）、校核（只能判断公式中的计算正误，不能 确认平衡方程本身是否列对）。
三、课堂练习
1、求图示梁的支座反力
解法一：
1）、取梁整体研究，作受力图
A 80KN Bຫໍສະໝຸດ 3mRA 6m3m
RB
2）、列平衡方程求解 （1）∑mA=0，RB×6﹣80 ×3=0，解之， RB=40KN（↑） （2）∑mB=0，RA ×6-80 ×3=0，解之， RA=40KN （↑） 3）、校核 ∵ ∑ Y= RA + RB –80=0 ∴计算无误
解法二：1）、取梁整体研究，作受力图
2）、由对称得
RA=RB=½×80=40KN(↑)
2、求图示梁的支座反力 解：1）、 取整体研究， 作受力图
mA A 20KN 2m 1m
XA
20KN
2m
YA
1m
2）、列平衡方程，求解
∑ Y= 0 ∑ X=0 ∑ mA=0 YA-20=0 XA=0 - mA+20×2=0 YA=20KN(↑) mA=40KN.m( 方向同图 )
四、小结
1、取研究对象，作受力图 2、列平衡方程，求解 3、校核
五、作业布置

解法二：1）、取梁整体研究，作受力图 2）、由对称得
RA=R图示梁的支座反力
解：1）、 取整体研究， 作受力图
A 20KN
2m
1m
XA
mA
20KN
2m
1m
YA
13
2）、列平衡方程，求解
∑ Y= 0 ∑ X=0 ∑ mA=0
YA-20=0 XA=0 - mA+20×2=0
（2）∑mB=0，RA ×6-40 ×4-10 × 2=0，解之， RA=30KN （↑）
3）校核 ∵ ∑ Y= RA + RB –40-10=0 ∴计算无误（只有支反
40KN A
10KN B
2m 2m 2m
力无误，才有可能作的内
力图正确）
6m
RA
RB
8
2、求下图所示悬臂梁的支座反力。
P=10KN A
直于梁轴线、向下。
5
二、新课--计算简单梁在集中 荷载作用下的支座反力
（一）、计算方法和步骤
1、选取研究对象，根据梁支座约束性质作梁 的受力图
2、根据平面平行力系平衡条件恰当列平 衡方程
1）对于简单梁常为：
∑X=0
∑Y=0
∑mA=0
2）恰当：一个方程含一个未知数
6
3、求解平衡方程、得支座反力。若计算值为正， 则表示支座反力值与受力图方向相同，反之与受
10
三、课堂练习
1、求图示梁的支座反力
解法一： 1）、取梁整体研究，作受力图
A 80KN
B
3m
3m
RA
6m
RB
11
2）、列平衡方程求解 （1）∑mA=0，RB×6﹣80 ×3=0，解之， RB=40KN（↑） （2）∑mB=0，RA ×6-80 ×3=0，解之， RA=40KN （↑）

开封黄河大桥
桥梁概况
主跨(Main Span)：50米 设计单位(Designed by)：河南省交通规划勘察设计院 施工单位(Constructed by)：河南省交通公路工程局 桥梁类型(Type of the Bridge)：梁桥、简支梁桥 所在地(Location)：河南、开封、黄河 全长(Length)：4475.09米 建成时间(completed year)：1989年
均布荷载q 连续梁桥 均布荷载q
(5).刚架桥 （combined bridges）
1)组成 2)受力特点 3)分类 4)实例
1)组成
主要由梁与立柱或墩柱刚性连接的桥梁。 刚架桥祖尧优点是：外形尺寸小，桥下静 孔大，桥下视野开阔，混凝土用梁少。但 钢筋的用量较大，基础的造价也较高。
2)受力特点
(3.)悬臂体系特点 由于支点负弯矩的卸载作用，跨中正 弯矩大大减小
由于弯矩图面积的减小，跨越能力增 大
体系形式：双悬臂、单悬臂、双悬臂 加挂孔、T形刚构 缺点行车条件不好
双悬臂梁桥 均布荷载q
单悬臂梁桥 均布荷载q
多跨悬臂梁桥 多跨连续梁桥
(4).连续梁桥的体系特点 1.由于支点负弯矩的卸载作用，跨中 正弯矩大大减小，恒载、活载均有 卸载作用 2.由于弯矩图面积的减小，跨越能力 增大 3.超静定结构，对基础变形及温差荷 载较敏感 4.行车条件好
二. 桥梁按承重结构静力体系划分的 结构体系
梁式桥
Hale Waihona Puke 图1.2.7 (a) 梁式桥
图1.2.7(b) 梁式桥
图1.2.15
1.梁桥
(1) 受力特点 (2) 分 类
(1) 受力特点
梁式桥是一种在竖向荷载作用下无水平反力的结构，由于外力(恒 载和活载)的作用方向与承重结构的轴线接近垂直，因而与同样跨径的 其它结构体系相比，梁桥产生的弯矩最大．通常需用抗弯、抗拉能力 强的材料(钢、配筋混凝土、钢—混凝土叠合结构等)来建造。

定义截面
13
截面名称：H 440×300×11/18 截面高度H= 440mm 宽度B=300mm 腹板厚度tw=11mm 翼缘厚度tf=18mm
Fluid Mechanics and Machinery 流 体 力 学 与 流 体 机 械
定义截面
14
显示截面特性值
Fluid Mechanics and Machinery 流 体 力 学 与 流 体 机 械
定义点格
21
点格：在用户坐标系UCS的x-y平面中显示点格 如果没有单独指定UCS，栅格自动 设置在全局坐标系GCS的X-Y平面中
Fluid Mechanics and Machinery 流 体 力 学 与 流 体 机 械
定义轴线 在用户坐标系UCS的x-y平面中显示轴线 22
x-y坐标系轴线
Fluid Mechanics and Machinery 流 体 力 学 与 流 体 机 械
9
数据库的内定名称Grade3即材料的名称
Fluid Mechanics and Machinery 流 体 力 学 与 流 体 机 械
10
Fluid Mechanics and Machinery 流 体 力 学 与 流 体 机 械
本例题的模型处于整体坐标系(Global Coordinate System, GCS)的X-Z平面，故可将 结构指定为二维结构(X-Z Plane)
Z
整体坐标系的 X-Z平面
是竖直平面
Y
整体坐标系的
X-Y平面
是水平平面
X
Fluid Mechanics and Machinery 流 体 力 学 与 流 体 机 械
Fluid Mechanics and Machinery 流 体 力 学 与 流 体 机 械

桥梁桥梁（bridge）指的是为道路跨越天然或人工障碍物而修建的建筑物，它架设在江河湖海上，使车辆行人等能顺利通行。

桥梁一般由上部结构、下部结构和附属构造物组成，上部结构主要指桥跨结构和支座系统；下部结构包括桥台、桥墩和基础；附属构造物则指桥头搭板、锥形护坡、护岸、导流工程等。

桥梁按照结构体系划分，有梁式桥、拱桥、刚架桥、悬索承重（悬索桥、斜拉桥）四种基本体系。

桥梁一般讲由五大部件和五小部件组成，五大部件是指桥梁承受汽车或其他车辆运输荷载的桥跨上部结构与下部结构，是桥梁结构安全的保证。

包括(1)桥跨结构(或称桥孔结构，上部结构)、(2)桥梁支座系统、(3)桥墩、桥台(4)承台(5)挖井或桩基。

五小部件是指直接与桥梁服务功能有关的部件，过去称为桥面构造。

包括(1)桥面铺装、(2)防排水系统、(3)栏杆、(4)伸缩缝、(5)灯光照明。

大型桥梁附属结构还有桥头堡，引桥等设置。

结构分类梁桥一般建在跨度很大，水域较浅处，由桥柱和桥板组成，物体重量从桥板传向桥柱。

拱桥一般建在跨度较小的水域之上，桥身成拱形，一般都有几个桥洞，起到泄洪的功能，桥中间的重量传向桥两端，而两端的则传向中间。

悬桥是如今最实用的一种桥，桥可以建在跨度大、水深的地方，由桥柱、铁索与桥面组成，早期的悬桥就已经可以经住风吹雨打，不会断掉，吊桥基本上可以在暴风来临时岿然不动。

按材料类型分为：木桥、石桥、圬工桥、钢筋砼桥、预应力桥、钢桥按承重构件受力情况可分：为梁桥、板桥、拱桥、钢结构桥、吊桥、组合体系桥（斜拉桥、悬索桥）1、按多孔跨径总长分：特大桥（L>1000m）；大桥（100m≤L≤1000m）；中桥（30m<L<100m);小桥（8m≤L≤30m）2、按单孔跨径分：特大桥（L>150m）；大桥（40m≤L≤150m）；中桥（20m《L<40m）;小桥(5m《L<20m);小于5m涵洞一、梁式桥梁式桥是指用梁或桁架梁作主要承重结构的桥梁。

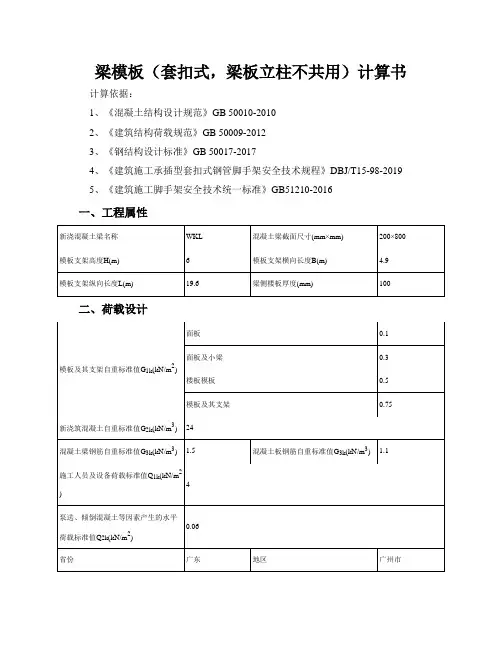
梁模板（套扣式，梁板立柱不共用）计算书计算依据：1、《混凝土结构设计规范》GB 50010-20102、《建筑结构荷载规范》GB 50009-20123、《钢结构设计标准》GB 50017-20174、《建筑施工承插型套扣式钢管脚手架安全技术规程》DBJ/T15-98-20195、《建筑施工脚手架安全技术统一标准》GB51210-2016一、工程属性二、荷载设计三、模板体系设计设计简图如下：平面图立面图四、面板验算面板类型覆面木胶合板面板厚度t(mm) 15面板抗弯强度设计值[f](N/mm2) 15 面板抗剪强度设计值[τ](N/mm2) 1.5面板弹性模量E(N/mm2) 10000取单位宽度b=1000mm，按简支梁计算：截面抵抗矩：W＝bt2/6=1000×15×15/6＝37500mm3，截面惯性矩：I＝bt3/12=1000×15×15×15/12＝281250mm4根据《建筑施工承插型套扣式钢管脚手架安全技术规程》DBJ/T15-98-2019第4.3节规定可知：q1＝γ0×[1.3(G1k+(G2k+G3k)×h)+1.5×Q1k]×b=1×[1.3×(0.1+(24+1.5)×0.8)+1.5×4]×1＝32. 65kN/mq2＝[1×(G1k+(G2k+G3k)×h)]×b＝[1×(0.1+(24+1.5)×0.8)]×1＝20.5kN/m计算简图如下：1、强度验算M max＝0.125q1L2＝0.125×32.65×0.22＝0.163kN·mσ＝M max/W＝0.163×106/37500＝4.353N/mm2≤[f]＝15N/mm2满足要求！2、挠度验算νmax＝5q2L4/(384EI)=5×20.5×2004/(384×10000×281250)＝0.152mm≤[ν]＝min[L/150，10]＝min[200/150，10]＝1.333mm满足要求！3、支座反力计算设计值(承载能力极限状态)R1=R2=0.5q1L=0.5×32.65×0.2＝3.265kN标准值(正常使用极限状态)R1'=R2'=0.5q2L=0.5×20.5×0.2＝2.05kN五、小梁验算梁侧存在混凝土板，故梁底支撑区域内楼板荷载需附加传递：承载能力极限状态：梁底面板传递给左边小梁线荷载：q1左＝R1/b=3.265/1＝3.265kN/m梁底面板传递给右边小梁线荷载：q1右＝R2/b=3.265/1＝3.265kN/m小梁自重：q2＝1×1.3×(0.3-0.1)×0.2/2 =0.026kN/m梁左侧模板传递给左边小梁荷载q3左＝1×1.3×0.5×(0.8-0.1)=0.455kN/m梁右侧模板传递给右边小梁荷载q3右＝1×1.3×0.5×(0.8-0.1)=0.455kN/m梁左侧楼板传递给左边小梁荷载q4左＝1×[1.3×(0.5+(24+1.1)×0.1)+1.5×4]×(0.65-0.2/2 )/2×1=2.726kN/m梁右侧楼板传递给右边小梁荷载q4右＝1×[1.3×(0.5+(24+1.1)×0.1)+1.5×4]×(0.65-0.2/2 )/2×1=2.726kN/m左侧小梁荷载q左＝q1左+q2+q3左+q4左 =3.265+0.026+0.455+2.726=6.472kN/m右侧小梁荷载q右＝q1右+q2+q3右+q4右 =3.265+0.026+0.455+2.726=6.472kN/m小梁最大荷载q=Max[q左,q右]=Max[6.472,6.472]=6.472kN/m正常使用极限状态：梁底面板传递给左边小梁线荷载：q1左'＝R1'/b=2.05/1＝2.05kN/m梁底面板传递给右边小梁线荷载：q1右'＝R2'/b=2.05/1＝2.05kN/m小梁自重：q2'＝1×(0.3-0.1)×0.2/2 =0.02kN/m梁左侧模板传递给左边小梁荷载q3左'＝1×0.5×(0.8-0.1)=0.35kN/m梁右侧模板传递给右边小梁荷载q3右'＝1×0.5×(0.8-0.1)=0.35kN/m梁左侧楼板传递给左边小梁荷载q4左'＝[1×(0.5+(24+1.1)×0.1)]×(0.65-0.2/2)/2×1=0.82 8kN/m梁右侧楼板传递给右边小梁荷载q4右'＝[1×(0.5+(24+1.1)×0.1)]×(0.65-0.2/2)/2×1=0.82 8kN/m左侧小梁荷载q左'＝q1左'+q2'+q3左'+q4左'=2.05+0.02+0.35+0.828=3.248kN/m右侧小梁荷载q右'＝q1右'+q2'+q3右'+q4右' =2.05+0.02+0.35+0.828=3.248kN/m小梁最大荷载q'=Max[q左',q右']=Max[3.248,3.248]=3.248kN/m为简化计算，按简支梁和悬臂梁分别计算，如下图：1、抗弯验算M max＝max[0.125ql12，0.5ql22]＝max[0.125×6.472×0.92，0.5×6.472×0.152]＝0.655kN·σ=M max/W=0.655×106/64000=10.239N/mm2≤[f]=15.444N/mm2满足要求！2、抗剪验算V max＝max[0.5ql1，ql2]＝max[0.5×6.472×0.9，6.472×0.15]＝2.912kNτmax=3V max/(2bh0)=3×2.912×1000/(2×60×80)＝0.91N/mm2≤[τ]=1.782N/mm2满足要求！3、挠度验算ν1＝5q'l14/(384EI)＝5×3.248×9004/(384×9350×256×104)＝1.159mm≤[ν]＝min[l1/150，10]=min[900/150，10]＝6mmν2＝q'l24/(8EI)＝3.248×1504/(8×9350×256×104)＝0.009mm≤[ν]＝min[2l2/150，10]=mi n[300/150，10]＝2mm满足要求！4、支座反力计算承载能力极限状态R max=max[qL1,0.5qL1+qL2]=max[6.472×0.9,0.5×6.472×0.9+6.472×0.15]=5.825kN 同理可得：梁底支撑小梁所受最大支座反力依次为R1=5.825kN,R2=5.825kN正常使用极限状态R max'=max[q'L1,0.5q'L1+q'L2]=max[3.248×0.9,0.5×3.248×0.9+3.248×0.15]=2.923kN 同理可得：梁底支撑小梁所受最大支座反力依次为R1'=2.923kN,R2'=2.923kN六、主梁验算主梁计算截面类型(mm) Ф48×3主梁抗弯强度设计值[f](N/mm2) 205主梁抗剪强度设计值[τ](N/mm2) 125 主梁截面抵抗矩W(cm3) 4.49主梁弹性模量E(N/mm2) 206000 主梁截面惯性矩I(cm4) 10.78可调托座内主梁根数 2 主梁受力不均匀系数0.6主梁自重忽略不计，主梁2根合并，其主梁受力不均匀系数=0.6,则单根主梁所受集中力为Ks×Rn，Rn为各小梁所受最大支座反力1、抗弯验算主梁弯矩图(kN·m)σ=M max/W=0.35×106/4490=77.84N/mm2≤[f]=205N/mm2满足要求！2、抗剪验算主梁剪力图(kN)V max＝3.495kNτmax=2V max/A=2×3.495×1000/424＝16.486N/mm2≤[τ]=125N/mm2满足要求！3、挠度验算主梁变形图(mm)νmax＝0.145mm≤[ν]＝min[L/150，10]=min[400/150，10]＝2.667mm满足要求！4、支座反力计算承载能力极限状态支座反力依次为R1=3.495kN，R2=3.495kN立柱所受主梁支座反力依次为P1=3.495/0.6=5.825kN，P2=3.495/0.6=5.825kN 七、可调托座验算可调托座最大受力N＝max[P1，P2]＝5.825kN≤[N]=30kN满足要求！八、立柱验算1、长细比验算h max=max(ηh,h'+2a)=max(1.1×1800,1200+2×500)=2200mmλ=h max/i=2200/15.9=138.365≤[λ]=150长细比满足要求！查表得：φ＝0.3572、风荷载计算M w＝γ0×φc×1.5×ωk×l a×h2/10＝1×0.9×1.5×0.169×0.9×1.82/10＝0.067kN·m3、稳定性计算P1＝5.825kN，P2＝5.825kN立柱最大受力N w＝max[P1，P2]+1×1.3×0.15×(6-0.8)+M w/l b＝max[5.825，5.825]+1.01 4+0.067/0.4＝7.005kNf＝N/(φA)+M w/W＝7005.321/(0.357×424)+0.067×106/4490＝61.202N/mm2≤[f]＝205N /mm2满足要求！九、高宽比验算根据《建筑施工承插型套扣式钢管脚手架安全技术规程》DBJ/T15-98-2019第6.1.7条H/B=6/4.9=1.224≤3H=6m<8m满足要求！十、架体抗倾覆验算混凝土浇筑前，倾覆力矩主要由风荷载产生，抗倾覆力矩主要由模板及支架自重产生M T=γ0×φc×γQ(ωk LHh2)=1×0.9×1.5×(0.169×19.6×6×6)=160.983kN·mM R=γG[G1k+0.15×H/(l a'×l b')]LB2/2=0.9×[0.5+0.15×6/(0.9×0.9)]×19.6×4.92/2=341.182kN ·mM T=160.983kN·m≤M R=341.182kN·m满足要求！混凝土浇筑时，倾覆力矩主要由泵送、倾倒混凝土等因素产生的水平荷载产生，抗倾覆力矩主要由钢筋、混凝土、模板及支架自重产生M T=γ0×φc×γQ(Q2k LH2)=1×0.9×1.5×(0.06×19.6×62)=57.154kN·mM R=γG[G1k+(G2k+G3k)h0+0.15×H/(l a'×l b')]LB2/2=0.9×[0.5+(24+1.1)×0.1+0.15×6/(0.9×0.9)]×19.6×4.92/2=872.72kN·mM T=57.154kN·m≤M R=872.72kN·m满足要求！十一、立柱支承面承载力验算F1=N=7.005kN1、受冲切承载力计算根据《混凝土结构设计规范》GB50010-2010第6.5.1条规定，见下表可得：βh=1，f t=0.638N/mm2，η=1，h0=h-20=130mm，u m =2[(a+h0)+(b+h0)]=960mmF=(0.7βh f t+0.25σpc，m)ηu m h0=(0.7×1×0.638+0.25×0)×1×960×130/1000=55.736kN≥F1=7. 005kN满足要求！2、局部受压承载力计算根据《混凝土结构设计规范》GB50010-2010第6.6.1条规定，见下表可得：f c=5.568N/mm2，βc=1，βl=(A b/A l)1/2=[(a+2b)×(b+2b)/(ab)]1/2=[(320)×(300)/(120×100)]1/2=2.828，A ln=ab=1200 0mm2F=1.35βcβl f c A ln=1.35×1×2.828×5.568×12000/1000=255.129kN≥F1=7.005kN满足要求！。

幕墙立柱计算讲座第一部分 立柱计算概述 第一章 幕墙荷载传递方式第二章 计算模型转换下面以明框立柱大样为例：根据立柱的实际支承条件，我们通常将立柱的力学模型分为简支梁、双跨梁、悬臂梁、多跨铰接静定连续梁。

1、 简支梁简支层间的竖剖节点为：简支层间的横剖节点为：简支梁力学模型是《玻璃幕墙工程技术规范》(JGJ102-2003)中推荐的立柱计算模型。

在均布荷载作用下，其简化图形如图1.1。

图1.1简支梁均布荷载对应的弯矩、剪力图：（幕墙设计还需要考虑竖向自重）由截面法可求得简支梁任意位置的弯矩为：xql x q M 222+-=进而可解得：当2/l x =时，有弯矩最大值：2max 125.0qlM =。

简支梁的变形可以按梁挠曲线的近似微分方程[1]：)22(22qx x ql dx y d EI --=经过两次积分可得简支梁的挠度方程为：)242412(1343x ql qx qlx EI y ---=由于梁上外力及边界条件对于梁跨中点都是对称的，因此梁的挠曲线也是对称的，则最大挠度截面发生在梁的中点位置。

即：当2/l x =时，代入上式有：EI l q f k 38454max =此种力学模型是目前我国幕墙行业使用的较广泛的形式，但由于没有考虑上下层立柱间的荷载的传递，因而计算结果偏于保守。

2、 双跨梁（一次超静定）双跨梁层间的竖剖节点为：在简支梁的计算中，由于挠度和弯矩偏大，为了提高梁的刚度和强度，就必须加大立柱截面，这样用料较大，在经济上也不太合算。

在简支梁中间适当位置增加一个支承，就形成了“双跨梁”，可以有效的减小梁的内力和挠度。

双跨梁简化图形如图3.1。

图3.1双跨梁为一次超静定结构，可以采用力法求解，但为节省时间，通常我们可以采用查静力手册。

双跨梁均布荷载作用下的弯矩和剪力图：以上简单介绍了双跨梁的力学模型，双跨梁在工程实际的应用是相当广泛的，它可以大大减少立柱的用料。

在工程中大多利用建筑结构的下翻梁或加设钢梁、钢架来增加支点。

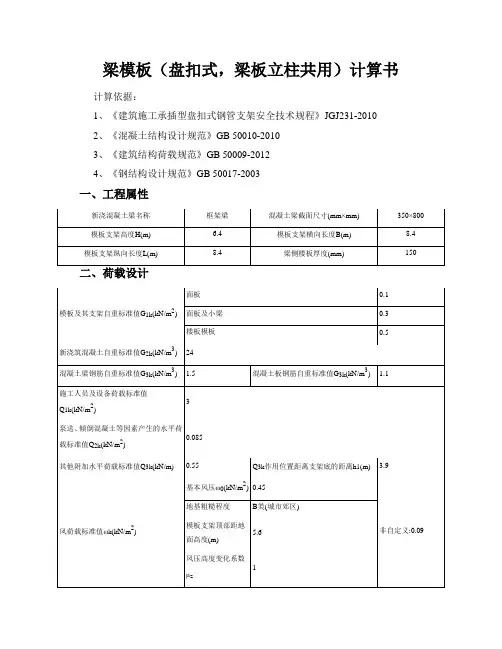
梁模板（盘扣式，梁板立柱共用）计算书计算依据：1、《建筑施工承插型盘扣式钢管支架安全技术规程》JGJ231-20102、《混凝土结构设计规范》GB 50010-20103、《建筑结构荷载规范》GB 50009-20124、《钢结构设计规范》GB 50017-2003一、工程属性平面图立面图四、面板验算W＝bh2/6=1000×15×15/6＝37500mm3，I＝bh3/12=1000×15×15×15/12＝281250mm4q1＝[1.2(G1k+(G2k+G3k)×h)+1.4×Q1k]×b=[1.2×(0.1+(24+1.5)×0.8)+1.4×3]×1＝28.8kN/mq1静＝1.2×[G1k+(G2k+G3k)×h]×b＝1.2×[0.1+(24+1.5)×0.8]×1＝24.6kN/mq1活＝1.4×Q1k×b＝1.4×3×1＝4.2kN/mq2＝[1×(G1k+(G2k+G3k)×h)+1×Q1k]×b＝[1×(0.1+(24+1.5)×0.8)+1×3]×1＝23.5kN/m计算简图如下：1、强度验算M max＝0.1q1静L2+0.117q1活L2＝0.1×24.6×0.1172+0.117×4.2×0.1172＝0.04kN·m σ＝M max/W＝0.04×106/37500＝1.071N/mm2≤[f]＝15N/mm2满足要求！2、挠度验算νmax＝0.677q2L4/(100EI)=0.677×23.5×116.6674/(100×10000×281250)＝0.01mm≤[ν]＝min[L/150，10]＝min[116.667/150，10]＝0.778mm满足要求！3、支座反力计算设计值(承载能力极限状态)R1=R4=0.4q1静L+0.45q1活L=0.4×24.6×0.117+0.45×4.2×0.117＝1.368kNR2=R3=1.1q1静L+1.2q1活L=1.1×24.6×0.117+1.2×4.2×0.117＝3.745kN标准值(正常使用极限状态)R1'=R4'=0.4q2L=0.4×23.5×0.117＝1.097kNR2'=R3'=1.1q2L=1.1×23.5×0.117＝3.016kN五、小梁验算承载能力极限状态：梁底面板传递给左边小梁线荷载：q1左＝R1/b=1.368/1＝1.368kN/m梁底面板传递给中间小梁最大线荷载：q1中＝Max[R2,R3]/b =Max[3.745,3.745]/1= 3.745kN/m梁底面板传递给右边小梁线荷载：q1右＝R4/b=1.368/1＝1.368kN/m小梁自重：q2＝1.2×(0.3-0.1)×0.35/3 =0.028kN/m梁左侧模板传递给左边小梁荷载q3左＝1.2×0.5×(0.8-0.15)=0.39kN/m梁右侧模板传递给右边小梁荷载q3右＝1.2×0.5×(0.8-0.15)=0.39kN/m梁左侧楼板传递给左边小梁荷载q4左＝[1.2×(0.5+(24+1.1)×0.15)+1.4×3]×(0.45-0.35/2)/2×1=1.281kN/m梁右侧楼板传递给右边小梁荷载q4右＝[1.2×(0.5+(24+1.1)×0.15)+1.4×3]×((0.9-0.45)-0.35/2)/2×1=1.281kN/m左侧小梁荷载q左＝q1左+q2+q3左+q4左=1.368+0.028+0.39+1.281=3.068kN/m 中间小梁荷载q中= q1中+ q2=3.745+0.028=3.773kN/m右侧小梁荷载q右＝q1右+q2+q3右+q4右=1.368+0.028+0.39+1.281=3.068kN/m 小梁最大荷载q=Max[q左,q中,q右]=Max[3.068,3.773,3.068]=3.773kN/m正常使用极限状态：梁底面板传递给左边小梁线荷载：q1左'＝R1'/b=1.097/1＝1.097kN/m梁底面板传递给中间小梁最大线荷载：q1中'＝Max[R2',R3']/b =Max[3.016,3.016]/1= 3.016kN/m梁底面板传递给右边小梁线荷载：q1右'＝R4'/b=1.097/1＝1.097kN/m小梁自重：q2'＝1×(0.3-0.1)×0.35/3 =0.023kN/m梁左侧模板传递给左边小梁荷载q3左'＝1×0.5×(0.8-0.15)=0.325kN/m梁右侧模板传递给右边小梁荷载q3右'＝1×0.5×(0.8-0.15)=0.325kN/m梁左侧楼板传递给左边小梁荷载q4左'＝[1×(0.5+(24+1.1)×0.15)+1×3]×(0.45-0.35/2)/2×1=0.999kN/m梁右侧楼板传递给右边小梁荷载q4右'＝[1×(0.5+(24+1.1)×0.15)+1×3]×((0.9-0.45)-0.35/2)/2×1=0.999kN/m左侧小梁荷载q左'＝q1左'+q2'+q3左'+q4左'=1.097+0.023+0.325+0.999=2.444kN/m中间小梁荷载q中'= q1中'+ q2'=3.016+0.023=3.039kN/m右侧小梁荷载q右'＝q1右'+q2'+q3右'+q4右' =1.097+0.023+0.325+0.999=2.444kN/m小梁最大荷载q'=Max[q左',q中',q右']=Max[2.444,3.039,2.444]=3.039kN/m为简化计算，按简支梁和悬臂梁分别计算，如下图：1、抗弯验算M max＝max[0.125ql12，0.5ql22]＝max[0.125×3.773×0.2252，0.5×3.773×0.152]＝0.042kN·mσ=M max/W=0.042×106/40830=1.04N/mm2≤[f]=15.44N/mm2满足要求！2、抗剪验算V max＝max[0.5ql1，ql2]＝max[0.5×3.773×0.225，3.773×0.15]＝0.566kNτmax=3V max/(2bh0)=3×0.566×1000/(2×50×70)＝0.243N/mm2≤[τ]=1.78N/mm2满足要求！3、挠度验算ν1＝5q'l14/(384EI)＝5×3.039×2254/(384×9350×142.92×104)＝0.008mm≤[ν]＝min[l1/150，10]=min[225/150，10]＝1.5mmν2＝q'l24/(8EI)＝3.039×1504/(8×9350×142.92×104)＝0.014mm≤[ν]＝min[2l2/150，10]=min[300/150，10]＝2mm满足要求！4、支座反力计算承载能力极限状态R max=[qL1,0.5qL1+qL2]=max[3.773×0.225,0.5×3.773×0.225+3.773×0.15]=0.99kN 同理可得：梁底支撑小梁所受最大支座反力依次为R1=0.805kN,R2=0.99kN,R3=0.99kN,R4=0.805kN正常使用极限状态R max'=[q'L1,0.5q'L1+q'L2]=max[3.039×0.225,0.5×3.039×0.225+3.039×0.15]=0.798kN 同理可得：梁底支撑小梁所受最大支座反力依次为R1'=0.642kN,R2'=0.798kN,R3'=0.798kN,R4'=0.642kN六、主梁验算1、抗弯验算主梁弯矩图(kN·m)σ=M max/W=0.609×106/3860=157.845N/mm2≤[f]=205N/mm2满足要求！2、抗剪验算主梁剪力图(kN)V max＝1.795kNτmax=2V max/A=2×1.795×1000/357＝10.056N/mm2≤[τ]=125N/mm2 满足要求！3、挠度验算主梁变形图(mm)νmax＝2.057mm≤[ν]＝min[L/150，10]=min[900/150，10]＝6mm 满足要求！4、支座反力计算承载能力极限状态支座反力依次为R1=1.795kN，R2=1.795kN正常使用极限状态支座反力依次为R1'=1.44kN，R2'=1.44kN七、纵向水平钢管验算1212 1.44]=1.44kN计算简图如下：1、抗弯验算纵向水平钢管弯矩图(kN·m) σ＝M max/W＝0.606×106/3860＝156.95N/mm2≤[f]=205N/mm2满足要求！2、抗剪验算纵向水平钢管剪力图(kN)V max＝3.814kNτmax＝2V max/A=2×3.814×1000/357＝21.369N/mm2≤[τ]＝125N/mm2满足要求！3、挠度验算纵向水平钢管变形图(mm)νmax＝1.452mm≤[ν]＝min(L/150，10)=min(900/150，10)＝6mm满足要求！4、支座反力计算支座反力依次为R1=3.814kN，R2=7.853kN，R3=7.853kN，R4=3.814kN同理可得：两侧立柱所受支座反力依次为R1=7.853kN，R2=7.853kN八、扣件抗滑移验算1、扣件抗滑移验算0.85×8=6.8kN<两侧立柱最大受力N＝max[R1,R2]＝max[7.853,7.853]＝7.853kN≤0.85×12=10.2kN双扣件在扭矩达到40～65N·m且无质量缺陷的情况下，双扣件能满足要求！九、立柱验算h max=max(ηh,h'+2ka)=max(1.2×1200,500+2×0.7×450)=1440mmλ=h max/i=1440/16.1=89.441≤[λ]=150长细比满足要求！查表得，υ＝0.6672、风荷载计算M w＝υc×1.4×ωk×l a×h2/10＝0.9×1.4×0.09×0.9×1.22/10＝0.015kN·m根据《建筑施工承插型盘扣式钢管支架安全技术规程》JGJ231-2010公式5.3.1-2：1)面板验算q1＝[1.2×(0.1+(24+1.5)×0.8)+1.4×0.9×3]×1＝28.38kN/m2)小梁验算q1＝max{1.346+1.2×[(0.3-0.1)×0.35/3+0.5×(0.8-0.15)]+[1.2×(0.5+(24+1.1)×0.15)+1.4×0.9×3]×max[0.45-0.35/2，(0.9-0.45)-0.35/2]/2×1，3.686+1.2×(0.3-0.1)×0.35/3}=3.714kN/m 同上四～七计算过程，可得：R1＝7.696kN，R2＝7.696kN立柱最大受力N w＝max[R1+N边1，R2+N边2]+1.2×0.15×(6.4-0.8)+M w/l b＝max[7.696+[1.2×(0.5+(24+1.1)×0.15)+1.4×0.9×3]×(0.9+0.45-0.35/2)/2×0.9，7.696+[1.2×(0.5+(24+1.1)×0.15)+1.4×0.9×3]×(0.9+0.9-0.45-0.35/2)/2×0.9]+1.008+0.01 5/0.9＝13.425kNf＝N/(υA)+M w/W＝13424.815/(0.667×357)+0.015×106/3860＝60.265N/mm2≤[f]＝205N/mm2满足要求！十、高宽比验算根据《建筑施工承插型盘扣式钢管支架安全技术规范》JGJ231-2010 第6.1.4: 对长条状的独立高支模架，架体总高度与架体的宽度之比不宜大于3H/B=6.4/8.4=0.762≤3满足要求！十一、架体抗倾覆验算混凝土浇筑前，倾覆力矩主要由风荷载产生，抗倾覆力矩主要由模板及支架自重产生M T=ψc×γQ(ωk LHh2+Q3k LHh1)=1×1.4×(0.09×8.4×6.4×2.92+0.55×8.4×6.4×3.9)=181.221 kN·mM R=γG[G1k+0.15×H/(l a'×l b')]LB2/2=0.9×[0.5+0.15×6.4/(0.9×0.9)]×8.4×8.42/2=449.467k N·mM T=181.221kN·m≤M R=449.467kN·m满足要求！混凝土浇筑时，倾覆力矩主要由泵送、倾倒混凝土等因素产生的水平荷载产生，抗倾覆力矩主要由钢筋、混凝土、模板及支架自重产生M T=ψc×γQ(Q2k LH2+Q3k LHh1)=1×1.4×(0.085×8.4×6.42+0.55×8.4×6.4×3.9)=202.385kN·mM R=γG[G1k+(G2k+G3k)h0+0.15×H/(l a'×l b')]LB2/2=0.9×[0.5+(24+1.1)×0.15+0.15×6.4/(0.9×0.9)]×8.4×8.42/2=1453.656kN·mM T=202.385kN·m≤M R=1453.656kN·m满足要求！十二、立柱支承面承载力验算11、受冲切承载力计算根据《混凝土结构设计规范》GB50010-2010第6.5.1条规定，见下表h t0u m =2[(a+h0)+(b+h0)]=1320mmF=(0.7βh f t+0.25σpc，)ηu m h0=(0.7×1×0.829+0.25×0)×1×1320×130/1000=99.579kN≥F1=13.425kN m满足要求！2、局部受压承载力计算根据《混凝土结构设计规范》GB50010-2010第6.6.1条规定，见下表c cβl=(A b/A l)1/2=[(a+2b)×(b+2b)/(ab)]1/2=[(600)×(600)/(200×200)]1/2=3，A ln=ab=40000mm2F=1.35βcβl f c A ln=1.35×1×3×8.294×40000/1000=1343.628kN≥F1=13.425kN 满足要求！。

简支梁和悬臂梁的弯矩挠度计算简支梁是在两个支点处支撑的梁，其中一个或两个支点可以是滑动支撑或铰接支撑。

悬臂梁是在一个端点处支撑的梁，另一端自由悬空。

这些梁的弯矩和挠度计算是通过应用梁的基本方程和适当的边界条件完成的。

首先，讨论简支梁的弯矩和挠度计算。

简支梁的弯矩是沿着梁的长度变化的力矩，可以通过梁的力学方程来计算。

在梁上选取一点x处的弯矩M(x)与该点处的弯矩图线性相关。

对于简支梁，弯矩是由横向力和弯曲力共同作用引起的。

弯矩可以根据梁的几何形状和受力情况进行计算。

根据梁受力分析，可以确定梁上各点的弯矩方程。

常见的情况包括均布载荷、集中力、不均布载荷等。

例如，对于均布载荷情况下的简支梁，弯矩方程可以通过积分计算得到。

具体计算步骤如下：1.确定梁的受力情况，如均布载荷情况下的简支梁。

2.假设载荷的作用范围为x=0到x=L。

3.在计算弯矩之前，需要确定几何参数，如梁的长度L、截面形状和尺寸等。

4.根据受力分析，可以得到梁上各点处的横向力和弯曲力。

5.根据梁的受力平衡条件，可以得到弯矩方程。

6.解弯矩方程，得到各点处的弯矩图。

7.根据需要，可以计算梁的最大弯矩和弯矩分布图。

接下来，我们将讨论悬臂梁的弯矩和挠度计算。

悬臂梁与简支梁的计算方法类似，但受力和边界条件有所不同。

悬臂梁只在一个端点支撑，另一端悬空。

根据这个约束条件，可以确定悬臂梁的边界条件。

通常情况下，悬臂梁的一个端点处的弯矩为零。

弯矩方程的求解步骤与简支梁类似。

需要根据梁的受力分析确定梁上各点处的横向力和弯曲力，然后应用梁的受力平衡条件得出弯矩方程。

解方程得到悬臂梁各点处的弯矩图。

与简支梁相比，悬臂梁的弯矩图在边界处有显著的变化，这是由于边界条件的不同引起的。

除了弯矩的计算，梁的挠度也是分析和设计的重要考虑因素之一、梁的挠度是指在加载过程中梁发生的纵向位移。

挠度计算需要应用梁的挠度方程和适当的边界条件。

挠度方程和边界条件的确定方法与弯矩类似。

通过梁受力分析确定梁上各点的挠度方程，并根据边界条件求解挠度方程。

桥梁的分类桥梁的分类方式很多，不同的分类方式有不同的桥梁类型，但就桥梁的结构的受力而言，总离不开拉压弯三种基本受力方式。

按照受力特点，主要分为以下五大类。

1、梁式桥特点:是一种在竖向荷载作用下无水平反力的结构。

由于外力作用方向与承重结构的轴线接近垂直，故与同跨径的其他结构体系相比，梁内产生的弯矩最大，通常需要抗弯能力强的材料(钢、钢筋混凝土等)来建造。

结构形式有:①简支梁桥:属于静定结构，受力明确，构造简单，施工方便，地基承载力要求低，是中小跨径桥梁常用的桥型②悬臂梁桥：将简支梁体向两端延伸，越过支点并与邻孔的梁段搭接或用铰轴衔接的桥跨结构便成为悬臂梁桥。

仅梁一端悬出的称为单悬臂梁，两端均悬出的称为双悬臂梁。

③连续梁桥：当上部承重结构连续跨过两个或两个以上桥孔，且沿桥跨方向无断开的桥梁便成为连续梁桥。

2、拱式桥特点：拱式桥的主要承载结构是拱圈或拱肋。

这种结构在竖向荷载作用下，拱的两端支承处除有竖向反力还有水平推力，正是这个水平推力显著削弱了荷载所引起的拱圈(或拱肋)内的弯矩。

因此，与同跨径的梁桥相比，拱桥的弯矩和变形要小很多。

拱桥通常采用抗压能力强的圬工材料(如石料、混凝土)、钢筋混凝土和钢来建造。

结构形式：（1）按照拱上建筑的型式，可分为实腹式拱桥和空腹式拱桥（2）按照桥面位置，可分为上承式拱桥中承式拱桥和下承式拱桥。

3、悬索桥特点：悬索桥，又名吊桥指的是以通过索塔悬挂并锚固于两岸（或桥两端）的缆索（或钢链）作为上部结构主要承重构件的桥梁。

其优点在于成卷的主缆易于运输，构件较轻，便于无支架悬吊拼装。

然而，相对于其他体系而言，悬索桥自重轻，结构刚度差，在车辆荷载和风荷载作用下，桥梁有较大的变形和振动。

结构形式：（1）按主缆锚固方式分为地锚式和自锚式两大类。

地锚式悬索桥的主缆拉力传递给地基。

它既可用于一般跨径的桥梁，也可用于特大跨径的桥梁。

（2）按孔跨布置形式可分为单跨悬索桥、三跨悬索桥和多跨悬索桥。

净跨径：对于设支座的桥梁为相邻两墩、台身顶内缘之间的水平净距，不设支座的桥梁为上、下部结构相交处内缘间的水平净距，用l0表示。

汽车冲击力：汽车以较高速度驶过桥梁时，由于桥面不平整、发动机震动等原因，会引起桥梁结构的振动，从而造成内力增大，这种动力效应称为冲击作用。

单向板：通常把板的长边和短边比大于或等于2的板称为单向板。

双向板：通常把板的长边和短边比小于2的板称为双向板，需按两个方向的内力配置钢筋。

板的有效工作宽度：板在局部分布荷载的作用下，不仅直接承压部分的板带参加工作，与其相邻的部分板带也会分担一部分荷载共同工作，因此在桥面板的计算中就需要确定板的有效工作宽度。

预拱度：为了消除恒载和经常作用活载之长期效应产生的挠度，通常需要在桥梁施工时设置反向挠度称为预拱度。

吻合束：按实际荷载作用下的弯矩图线形作为束曲线的线形，便是吻合束的线形计算矢高：拱顶截面形心至相邻两拱脚截面形心之连线的垂直距离。

矢跨比：拱圈的净矢高与净跨径之比或计算矢高与计算跨径之比。

拱轴线：拱圈各横向截面或换算截面的形心连线。

合理拱轴线：当拱的轴线与压力线完全重合时，各截面的弯矩和剪力都为零，只有轴力，各截面上产生均匀分布的正应力，材料能得到充分利用，从力学观点上看，这是最经、合理的，因此，在某种固定荷载作用下，拱的所有截面的弯矩均为零的轴线称为拱的合理拱轴线。

剪力铰：是一种传递竖向剪力，但不能传递水平推力和弯矩的联合构造。

假载法：通过改变拱轴系数来变更拱轴线，使拱顶、拱脚两截面的控制应力相近相等。

拱轴系数：m=gj/gd,其中gj为拱脚处结构自重集度，gd为拱顶处结构自重集度。

五点重合法：要求拱轴线在全拱有五点（拱顶、两1/4点和两拱脚）与其相应三铰结构自重压力线重合的确定悬链线拱的拱轴系数m的方法。

劲性骨架钢筋混泥土拱桥：主体结构由充满混凝土的钢管构成，再再钢管搭成的骨架上绑扎钢筋浇筑混凝土。

钢管混凝土拱桥：主拱圈由充满混凝土的钢管拼接而成。

大学物理实验讲义实验10杨氏模量的测定实验 1 拉伸法测量杨氏模量杨氏弹性模量(以下简称杨氏模量)是表征固体材料性质的重要的力学参量，它反映材料弹性形变的难易程度，在机械设计及材料性能研究中有着广泛的应用。

其测量方法有静态拉伸法、悬臂梁法、简支梁法、共振法、脉冲波传输法，后两种方法测量精度较高；本实验采用静态拉伸法测量金属丝的杨氏模量，因涉及多个长度量的测量，需要研究不同测量对象如何选择不同的测量仪器。

【实验目的】1. 学习用静态拉伸法测量金属丝的杨氏模量。

2. 掌握钢卷尺、螺旋测微计和读数显微镜的使用。

3. 学习用逐差法和作图法处理数据。

4. 掌握不确定度的评定方法。

【仪器用具】杨氏模量测量仪（包括砝码、待测金属丝）、螺旋测微计、钢卷尺、读数显微镜【实验原理】1. 杨氏模量的定义本实验讨论最简单的形变——拉伸形变，即棒状物体(或金属丝 )仅受轴向外力作用后F 与应变L的伸长或缩短。

按照胡克定律：在弹性限度内，弹性体的应力成正比。

SL设有一根原长为l ，横截面积为 S 的金属丝（或金属棒），在外力 F 的作用下伸长了L ，则根据胡克定律有F E( L)（ 1-1）SL式中的比例系数 E 称为杨氏模量，单位为 Pa （或N · m –2）。

实验证明，杨氏模量E 与外力 F 、金属丝的长度L 、横截面积 S 的大小无关，它只与制成金属丝的材料有关。

若金属丝的直径为d ，则 S1 d 2，代入（ 1-1）式中可得 44FLE（ 1-2）d 2 L（1-2）式表明，在长度、直径和所加外力相同的情况下，杨氏模量大的金属丝伸长量较小，杨氏模量小的金属丝伸长量较大。

因此，杨氏模量反映了材料抵抗外力引起的拉伸（或压缩）形变的能力。

实验中，测量出F、 L、 d、 L 值就可以计算出金属丝的杨氏模量 E 。

2.静态拉伸法的测量方法测量金属丝的杨氏模量的方法就是将金属丝悬挂于支架上，上端固定，下端加砝码对金属丝 F ，测出金属丝的伸长量L ，即可求出 E 。

图方向相反。
4、校核。（检查列的平衡方程和计算是否正确） （二）、例题 1、求下图所示简支梁的支座反力RA、RB。
40KN A
10KN B
2m 2m 2m
6m
编辑版
7
解：1）、取整体为研究对象，作受力图
2）、列平衡方程、求解
（1）∑mA=0，RB×6﹣40 ×2-1 0 ×4=0，解之，
RB=20KN（↑）
YA-20=0 XA=0 - mA+20×2=0
YA=20KN(↑) mA=40KN.m( 方向同图 )
四、小结
1、取研究对象，作受力图 2、列平衡方程，求解 3、校核
五、作业布置
编辑版
14
约束性质
（1）简支梁
A
B
A处为固定铰支座，B处为可
动铰支座（若AB梁上的作 XA
用力垂直于AB轴线，则
XA=0，YA=RA
编辑版
10
三、课堂练习
1、求图示梁的支座反力
解法一： 1）、取梁整体研究，作受力图
A 80KN
B
3m
3m
RA
6m
RB
编辑版
11
2）、列平衡方程求解 （1）∑mA=0，RB×6﹣80 ×3=0，解之， RB=40KN（↑） （2）∑mB=0，RA ×6-80 ×3=0，解之， RA=40KN （↑）
编辑版
1
编辑版
2
引入 《建筑力学》课件
新课 ————计算简单梁在集中荷载作
练习
用下的支座反力
小结
作业
大庆市建设中等职业技术学校
李福占
编辑版
3
一、引入
1、建筑工程中常见 的简单梁
1）、简支梁

梁模板（轮扣式，梁板立柱共用）计算书计算依据：1、《建筑施工脚手架安全技术统一标准》GB51210-20162、《建筑施工模板安全技术规范》JGJ162-20083、《混凝土结构设计规范》GB 50010-20104、《建筑结构荷载规范》GB 50009-20125、《钢结构设计规范》GB 50017-2003一、工程属性二、荷载设计风荷载参数：三、模板体系设计设计简图如下：平面图立面图四、面板验算取单位宽度b=1000mm，按四等跨连续梁计算：W＝bh2/6=1000×15×15/6＝37500mm3，I＝bh3/12=1000×15×15×15/12＝281250mm4 q1＝γ0×max[1.2(G1k+(G2k+G3k)×h)+1.4Q1k，1.35(G1k+(G2k+G3k)×h)+1.4ψc Q1k]×b=1.1×max[1.2×(0.1+(24+1.5)×2.3)+1.4×3，1.35×(0.1+(24+1.5)×2.3)+1.4×0.7×3]×1＝90.478k N/mq1静＝γ0×1.35×[G1k+(G2k+G3k)×h]×b＝1.1×1.35×[0.1+(24+1.5)×2.3]×1＝87.244kN/m q1活＝γ0×1.4×0.7×Q1k×b＝1.1×1.4×0.7×3×1＝3.234kN/mq2＝[1×(G1k+(G2k+G3k)×h)]×b＝[1×(0.1+(24+1.5)×2.3)]×1＝58.75kN/m计算简图如下：1、强度验算M max＝0.107q1静L2+0.121q1活L2＝0.107×87.244×0.1132+0.121×3.234×0.1132＝0.123kN ·mσ＝M max/W＝0.123×106/37500＝3.283N/mm2≤[f]＝26N/mm2满足要求！2、挠度验算νmax＝0.632q2L4/(100EI)=0.632×58.75×112.54/(100×9000×281250)＝0.023mm≤[ν]＝mi n[L/150，10]＝min[112.5/150，10]＝0.75mm满足要求！3、支座反力计算设计值(承载能力极限状态)R1=R5=0.393q1静L+0.446q1活L=0.393×87.244×0.113+0.446×3.234×0.113＝4.02kNR2=R4=1.143q1静L+1.223q1活L=1.143×87.244×0.113+1.223×3.234×0.113＝11.663kN R3=0.928q1静L+1.142q1活L=0.928×87.244×0.113+1.142×3.234×0.113＝9.524kN 标准值(正常使用极限状态)R1'=R5'=0.393q2L=0.393×58.75×0.113＝2.597kNR2'=R4'=1.143q2L=1.143×58.75×0.113＝7.555kNR3'=0.928q2L=0.928×58.75×0.113＝6.133kN五、小梁验算承载能力极限状态：梁底面板传递给左边小梁线荷载：q1左＝R1/b=4.02/1＝4.02kN/m梁底面板传递给中间小梁最大线荷载：q1中＝Max[R2,R3,R4]/b =Max[11.663,9.524,11.663]/1= 11.663kN/m梁底面板传递给右边小梁线荷载：q1右＝R5/b=4.02/1＝4.02kN/m小梁自重：q2＝1.1×1.35×(0.3-0.1)×0.45/4 =0.033kN/m梁左侧模板传递给左边小梁荷载q3左＝1.1×1.35×0.5×(2.3-0.25)=1.522kN/m梁右侧模板传递给右边小梁荷载q3右＝1.1×1.35×0.5×(2.3-0.25)=1.522kN/m梁左侧楼板传递给左边小梁荷载q4左＝1.1×Max[1.2×(0.5+(24+1.1)×0.25)+1.4×3，1.3 5×(0.5+(24+1.1)×0.25)+1.4×0.7×3]×(0.45-0.45/2)/2×1=1.526kN/m梁右侧楼板传递给右边小梁荷载q4右＝1.1×Max[1.2×(0.5+(24+1.1)×0.25)+1.4×3，1.3 5×(0.5+(24+1.1)×0.25)+1.4×0.7×3]×((0.9-0.45)-0.45/2)/2×1=1.526kN/m左侧小梁荷载q左＝q1左+q2+q3左+q4左 =4.02+0.033+1.522+1.526=7.101kN/m中间小梁荷载q中= q1中+ q2=11.663+0.033=11.697kN/m右侧小梁荷载q右＝q1右+q2+q3右+q4右 =4.02+0.033+1.522+1.526=7.101kN/m小梁最大荷载q=Max[q左,q中,q右]=Max[7.101,11.697,7.101]=11.697kN/m正常使用极限状态：梁底面板传递给左边小梁线荷载：q1左'＝R1'/b=2.597/1＝2.597kN/m梁底面板传递给中间小梁最大线荷载：q1中'＝Max[R2',R3',R4']/b =Max[7.555,6.133,7.555]/1= 7.555kN/m梁底面板传递给右边小梁线荷载：q1右'＝R5'/b=2.597/1＝2.597kN/m小梁自重：q2'＝1×(0.3-0.1)×0.45/4 =0.022kN/m梁左侧模板传递给左边小梁荷载q3左'＝1×0.5×(2.3-0.25)=1.025kN/m梁右侧模板传递给右边小梁荷载q3右'＝1×0.5×(2.3-0.25)=1.025kN/m梁左侧楼板传递给左边小梁荷载q4左'＝[1×(0.5+(24+1.1)×0.25)]×(0.45-0.45/2)/2×1=0. 762kN/m梁右侧楼板传递给右边小梁荷载q4右'＝[1×(0.5+(24+1.1)×0.25)]×((0.9-0.45)-0.45/2)/2×1=0.762kN/m左侧小梁荷载q左'＝q1左'+q2'+q3左'+q4左'=2.597+0.022+1.025+0.762=4.407kN/m 中间小梁荷载q中'= q1中'+ q2'=7.555+0.022=7.577kN/m右侧小梁荷载q右'＝q1右'+q2'+q3右'+q4右' =2.597+0.022+1.025+0.762=4.407kN/m 小梁最大荷载q'=Max[q左',q中',q右']=Max[4.407,7.577,4.407]=7.577kN/m为简化计算，按简支梁和悬臂梁分别计算，如下图：1、抗弯验算M max＝max[0.125ql12，0.5ql22]＝max[0.125×11.697×0.32，0.5×11.697×0.12]＝0.132k N·mσ=M max/W=0.132×106/54000=2.437N/mm2≤[f]=14.52N/mm2满足要求！2、抗剪验算V max＝max[0.5ql1，ql2]＝max[0.5×11.697×0.3，11.697×0.1]＝1.755kNτmax=3V max/(2bh0)=3×1.755×1000/(2×40×90)＝0.731N/mm2≤[τ]=1.716N/mm2满足要求！3、挠度验算ν1＝5q'l14/(384EI)＝5×7.577×3004/(384×7700×243×104)＝0.043mm≤[ν]＝min[l1/150，10]=min[300/150，10]＝2mmν2＝q'l24/(8EI)＝7.577×1004/(8×7700×243×104)＝0.005mm≤[ν]＝min[2l2/150，10]=mi n[200/150，10]＝1.333mm满足要求！4、支座反力计算承载能力极限状态R max=max[qL1,0.5qL1+qL2]=max[11.697×0.3,0.5×11.697×0.3+11.697×0.1]=3.509kN 同理可得：梁底支撑小梁所受最大支座反力依次为R1=2.13kN,R2=3.509kN,R3=2.867kN,R4=3.50 9kN,R5=2.13kN正常使用极限状态R max'=max[q'L1,0.5q'L1+q'L2]=max[7.577×0.3,0.5×7.577×0.3+7.577×0.1]=2.273kN 同理可得：梁底支撑小梁所受最大支座反力依次为R1'=1.322kN,R2'=2.273kN,R3'=1.847kN,R4'=2. 273kN,R5'=1.322kN六、主梁验算1、抗弯验算主梁弯矩图(kN·m)σ=M max/W=0.127×106/4120=30.802N/mm2≤[f]=205N/mm2 满足要求！2、抗剪验算主梁剪力图(kN)V max＝2.131kNτmax=2V max/A=2×2.131×1000/384＝11.097N/mm2≤[τ]=125N/mm2满足要求！3、挠度验算主梁变形图(mm)νmax＝0.01mm≤[ν]＝min[L/150，10]=min[225/150，10]＝1.5mm满足要求！4、支座反力计算承载能力极限状态支座反力依次为R1=0.188kN，R2=3.696kN，R3=7.128kN，R4=3.697kN，R5=0.188k N正常使用极限状态支座反力依次为R1'=0.122kN，R2'=2.337kN，R3'=4.607kN，R4'=2.337kN，R5'=0.122 kN七、2号主梁验算P＝max[R2，R3，R4]=Max[3.696，7.128，3.697]=7.128kN，P'＝max[R2'，R3'，R4']＝Max[2.337，4.607，2.337]=4.607kN1、抗弯验算2号主梁弯矩图(kN·m)σ=M max/W=0.802×106/4120=194.637N/mm2≤[f]=205N/mm2满足要求！2、抗剪验算2号主梁剪力图(kN)V max＝4.455kNτmax=2V max/A=2×4.455×1000/384＝23.204N/mm2≤[τ]=125N/mm2满足要求！3、挠度验算2号主梁变形图(mm)νmax＝0.639mm≤[ν]＝min(L/150，10)=min(600/150，10)＝4mm满足要求！4、支座反力计算极限承载能力状态支座反力依次为R1=9.801kN，R2=13.365kN，R3=5.346kN立杆所受主梁支座反力依次为R2=6.93/1=6.93kN，R3=13.365/1=13.365kN，R4=6.93 2/1=6.932kN八、纵向水平钢管验算P＝max[R1，R5]=0.188kN，P'＝max[R1'，R5']＝0.122kN 计算简图如下：1、抗弯验算纵向水平钢管弯矩图(kN·m) σ＝M max/W＝0.021×106/3860＝5.479N/mm2≤[f]＝205N/mm2 满足要求！2、抗剪验算纵向水平钢管剪力图(kN) V max＝0.118kNτmax＝2V max/A=2×0.118×1000/357＝0.658N/mm2≤[τ]＝125N/mm2 满足要求！3、挠度验算纵向水平钢管变形图(mm) νmax＝0.018mm≤[ν]＝min(L/150，10)=min(600/150，10)＝4mm满足要求！4、支座反力计算支座反力依次为R1=0.258kN，R2=0.353kN，R3=0.141kN同理可得：两侧立杆所受支座反力依次为R1=0.353kN，R5=0.353kN 九、可调托座验算1、扣件抗滑移验算两侧立杆最大受力N＝max[R1,R5]＝max[0.353,0.353]＝0.353kN≤0.85×8=6.8kN 单扣件在扭矩达到40～65N·m且无质量缺陷的情况下，单扣件能满足要求！2、可调托座验算可调托座最大受力N＝max[R2，R3，R4]＝13.365kN≤[N]=30kN满足要求！十、立杆验算1、长细比验算h max=max(ηh,h'+2ka)=max(1.2×1200,1200+2×0.7×300)=1620mmλ=h max/i=1620/16.1=100.621≤[λ]=150长细比满足要求！查表得：φ＝0.5882、风荷载计算M wd＝γ0×φc×γQ×Mωk=γ0×φc×γQ×(ζ2×ωk×(l a1+l a2)/2×h2/10)＝1.1×0.6×1.4×(1×0.024×0.45×1.22/10)＝0.001kN·m3、稳定性计算R1＝0.353kN，R2＝6.93kN，R3＝13.365kN，R4＝6.932kN，R5＝0.353kN梁两侧立杆承受楼板荷载：左侧楼板传递给梁左侧立杆荷载:N边1=1.1×max[1.2×(0.5+(24+1.1)×0.25)+1.4×3，1.35×(0.5+(24+1.1)×0.25)+0.7×1.4×3]×(0.9+0.45-0.45/2)/2×(0.6+0.3)/2=3.433kN右侧楼板传递给梁右侧立杆荷载:N边2=1.1×max[1.2×(0.5+(24+1.1)×0.25)+1.4×3，1.3 5×(0.5+(24+1.1)×0.25)+0.7×1.4×3]×(0.9+0.9-0.45-0.45/2)/2×(0.6+0.3)/2=3.433kNN d＝max[R1+N边1，R2，R3，R4，R5+N边2]+1.1×1.35×0.15×(5.8-2.3)＝max[0.353+3.4 33，6.93，13.365，6.932，0.353+3.433]+0.78＝14.145kNf d＝N d/(φA)+M wd/W＝14145.041/(0.588×357)+0.001×106/3860＝67.643N/mm2≤[f]＝2 05N/mm2满足要求！十一、高宽比验算根据《建筑施工脚手架安全技术统一标准》GB51210-2016 第8.3.2条:支撑脚手架独立架体高宽比不应大于3.0H/B=5.8/50=0.116≤3满足要求！十二、架体抗倾覆验算支撑脚手架风线荷载标准值:q wk=l'a×ωfk=0.9×0.493=0.444kN/m：风荷载作用在支架外侧竖向封闭栏杆上产生的水平力标准值：F wk= l'a×H m×ωmk=0.9×1.5×0.153=0.207kN支撑脚手架计算单元在风荷载作用下的倾覆力矩标准值M ok：M ok=0.5H2q wk+HF wk=0.5×5.82×0.444+5.8×0.207=8.661kN.m参考《规范》GB51210-2016 第6.2.17条：B2l'a(g k1+ g k2)+2ΣG jk b j≥3γ0M okg k1——均匀分布的架体面荷载自重标准值kN/m2g k2——均匀分布的架体上部的模板等物料面荷载自重标准值kN/m2G jk——支撑脚手架计算单元上集中堆放的物料自重标准值kNb j——支撑脚手架计算单元上集中堆放的物料至倾覆原点的水平距离mB2l'a(g k1+ g k2)+2ΣG jk b j=B2l'a[qH/(l'a×l'b)+G1k]+2×G jk×B/2=502×0.9×[0.15×5.8/(0.9×0.9)+0.5]+2×1×50/2=3591. 667kN.m≥3γ0M ok =3×1.1×8.661=28.581kN.M满足要求！。